Engineering Mathematics Questions and Solutions
VerifiedAdded on 2022/11/19
|33
|3450
|288
AI Summary
This document contains solutions to Engineering Mathematics questions related to Kirchoff's laws, Thevenin's equivalent circuit, waveform conversion, low pass filter, and series RLC circuit. It includes calculations for reactance, impedance, current, voltage drop, and gain.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

SOLUTION REPORT
FOR
ENGINEERING MATHEMATICS QUESTION
FOR
ENGINEERING MATHEMATICS QUESTION
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
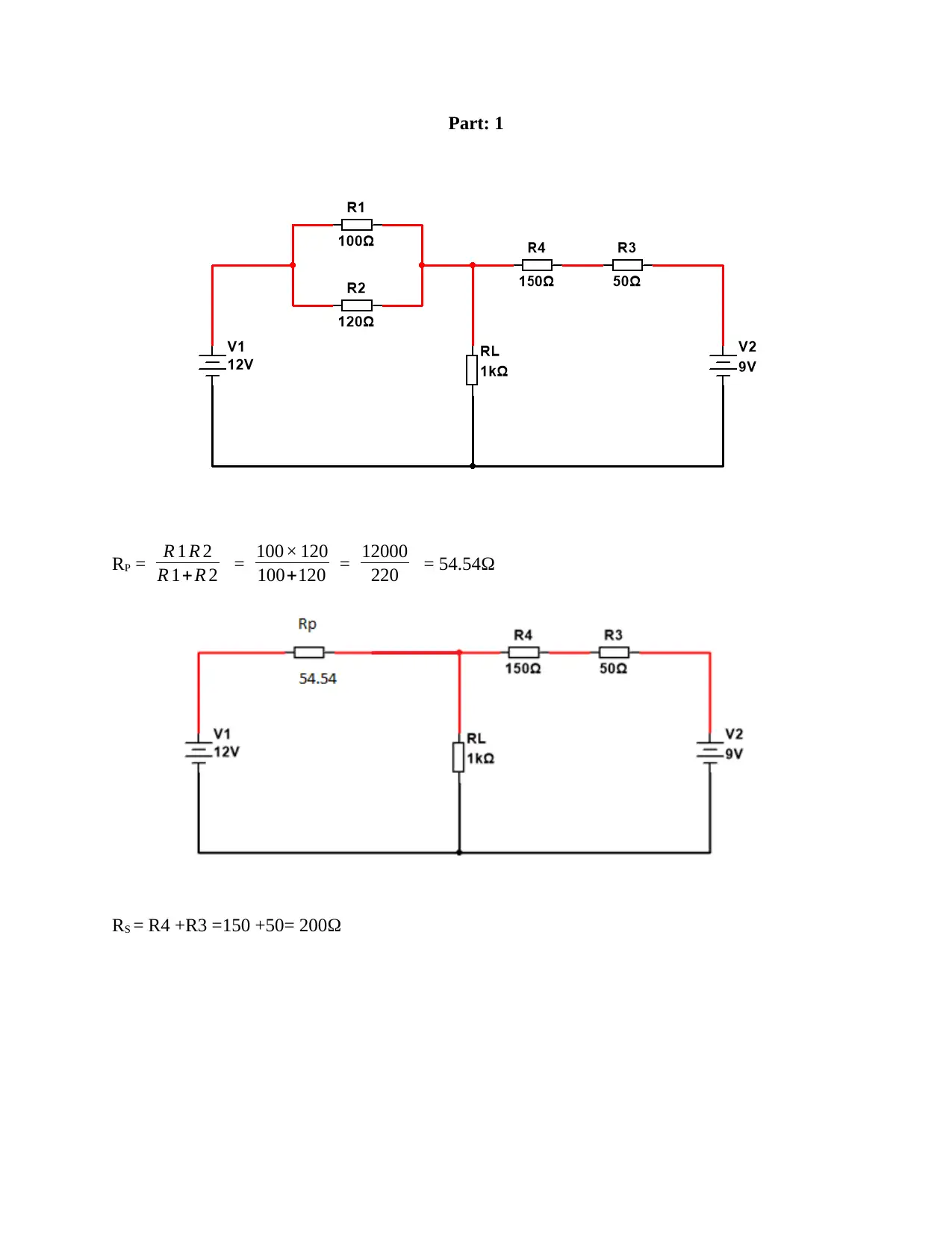
Part: 1
RP = R 1 R 2
R 1+R 2 = 100× 120
100+120 = 12000
220 = 54.54Ω
RS = R4 +R3 =150 +50= 200Ω
RP = R 1 R 2
R 1+R 2 = 100× 120
100+120 = 12000
220 = 54.54Ω
RS = R4 +R3 =150 +50= 200Ω
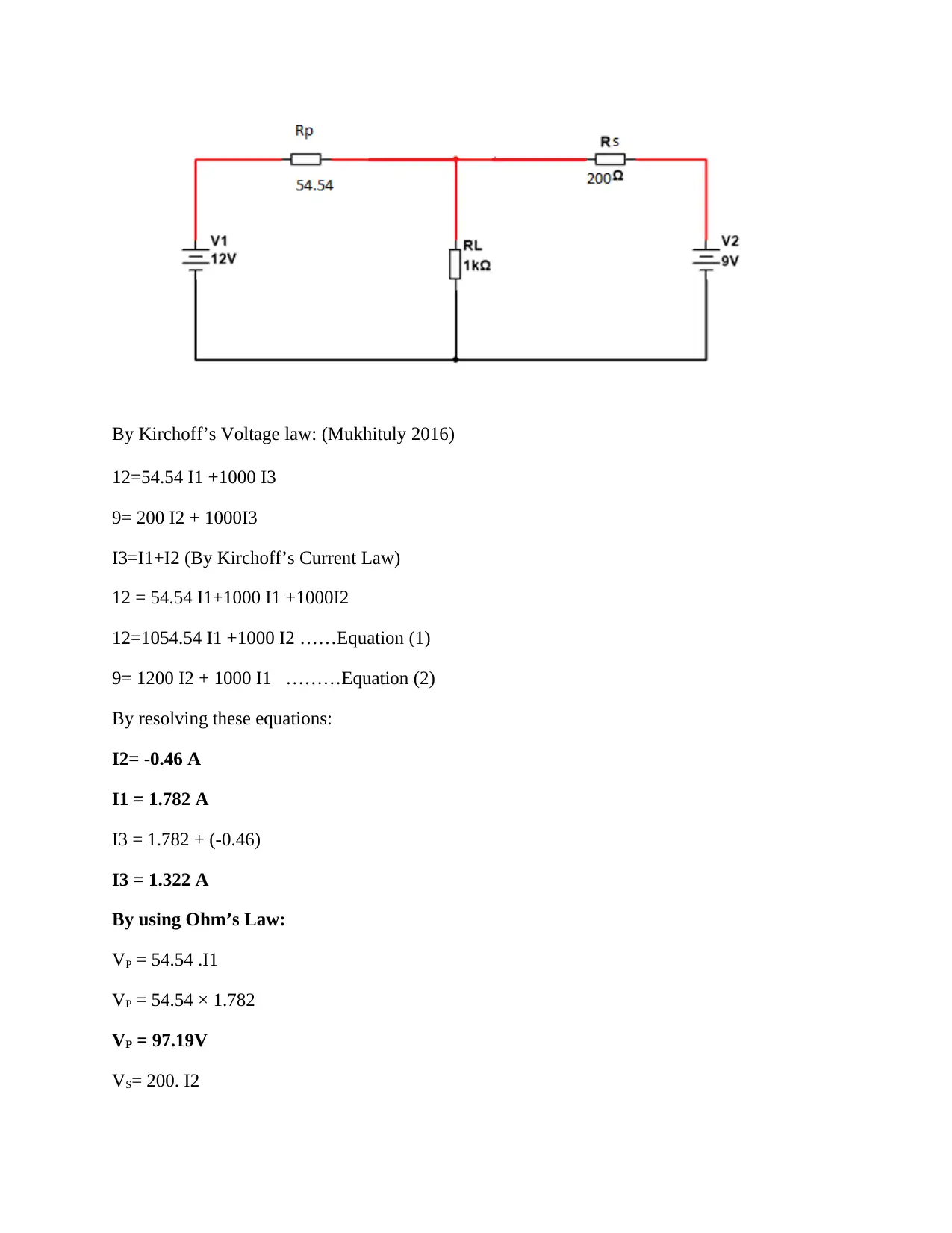
By Kirchoff’s Voltage law: (Mukhituly 2016)
12=54.54 I1 +1000 I3
9= 200 I2 + 1000I3
I3=I1+I2 (By Kirchoff’s Current Law)
12 = 54.54 I1+1000 I1 +1000I2
12=1054.54 I1 +1000 I2 ……Equation (1)
9= 1200 I2 + 1000 I1 ………Equation (2)
By resolving these equations:
I2= -0.46 A
I1 = 1.782 A
I3 = 1.782 + (-0.46)
I3 = 1.322 A
By using Ohm’s Law:
VP = 54.54 .I1
VP = 54.54 × 1.782
VP = 97.19V
VS= 200. I2
12=54.54 I1 +1000 I3
9= 200 I2 + 1000I3
I3=I1+I2 (By Kirchoff’s Current Law)
12 = 54.54 I1+1000 I1 +1000I2
12=1054.54 I1 +1000 I2 ……Equation (1)
9= 1200 I2 + 1000 I1 ………Equation (2)
By resolving these equations:
I2= -0.46 A
I1 = 1.782 A
I3 = 1.782 + (-0.46)
I3 = 1.322 A
By using Ohm’s Law:
VP = 54.54 .I1
VP = 54.54 × 1.782
VP = 97.19V
VS= 200. I2

VS= 200 × -0.46 A (- sign shows the opposite direction of current so by neglecting it)
VS= 92 V
VL =1000.I3
VL =1000× 1.322
VL = 1322 V
VS= 92 V
VL =1000.I3
VL =1000× 1.322
VL = 1322 V
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
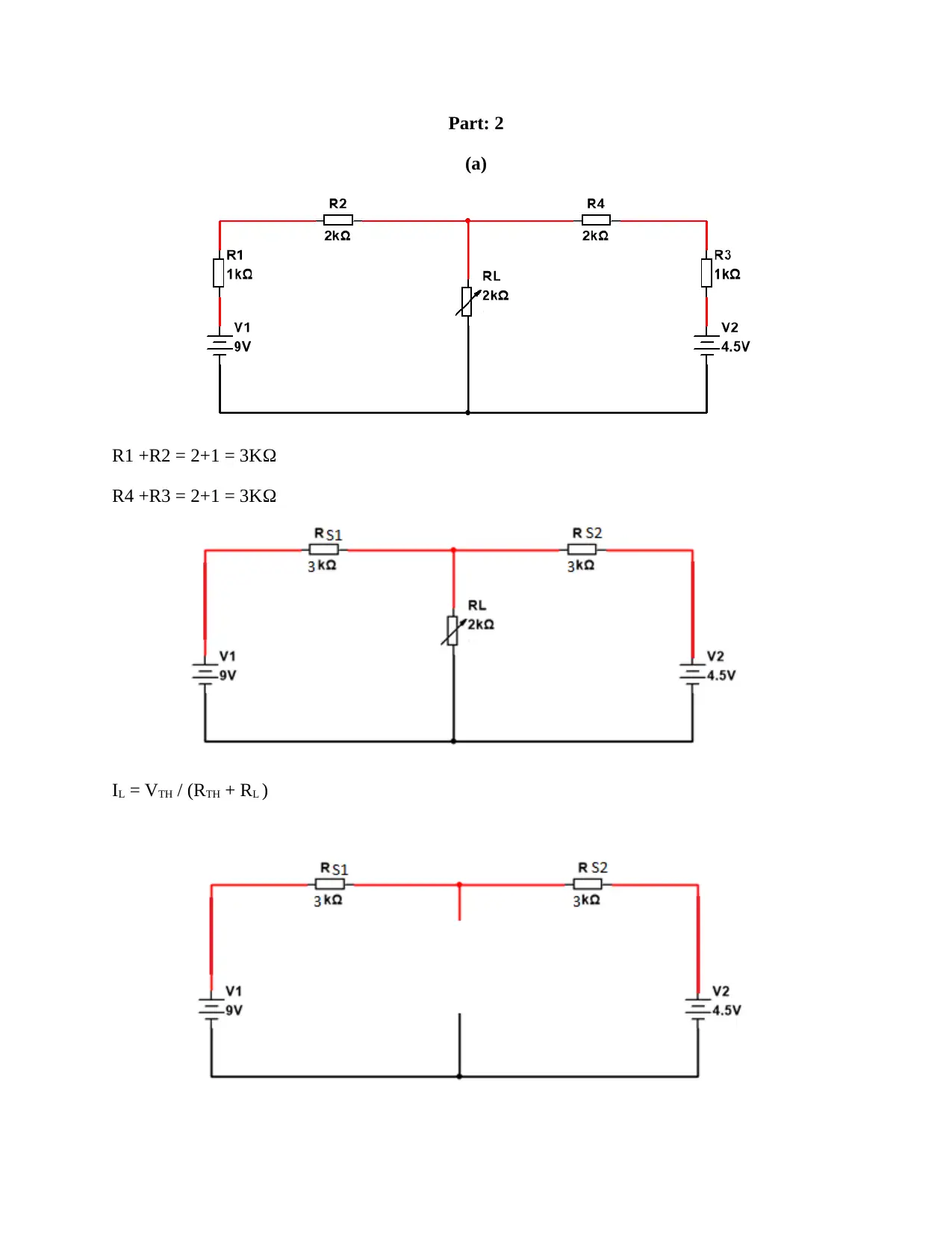
Part: 2
(a)
R1 +R2 = 2+1 = 3KΩ
R4 +R3 = 2+1 = 3KΩ
IL = VTH / (RTH + RL )
(a)
R1 +R2 = 2+1 = 3KΩ
R4 +R3 = 2+1 = 3KΩ
IL = VTH / (RTH + RL )
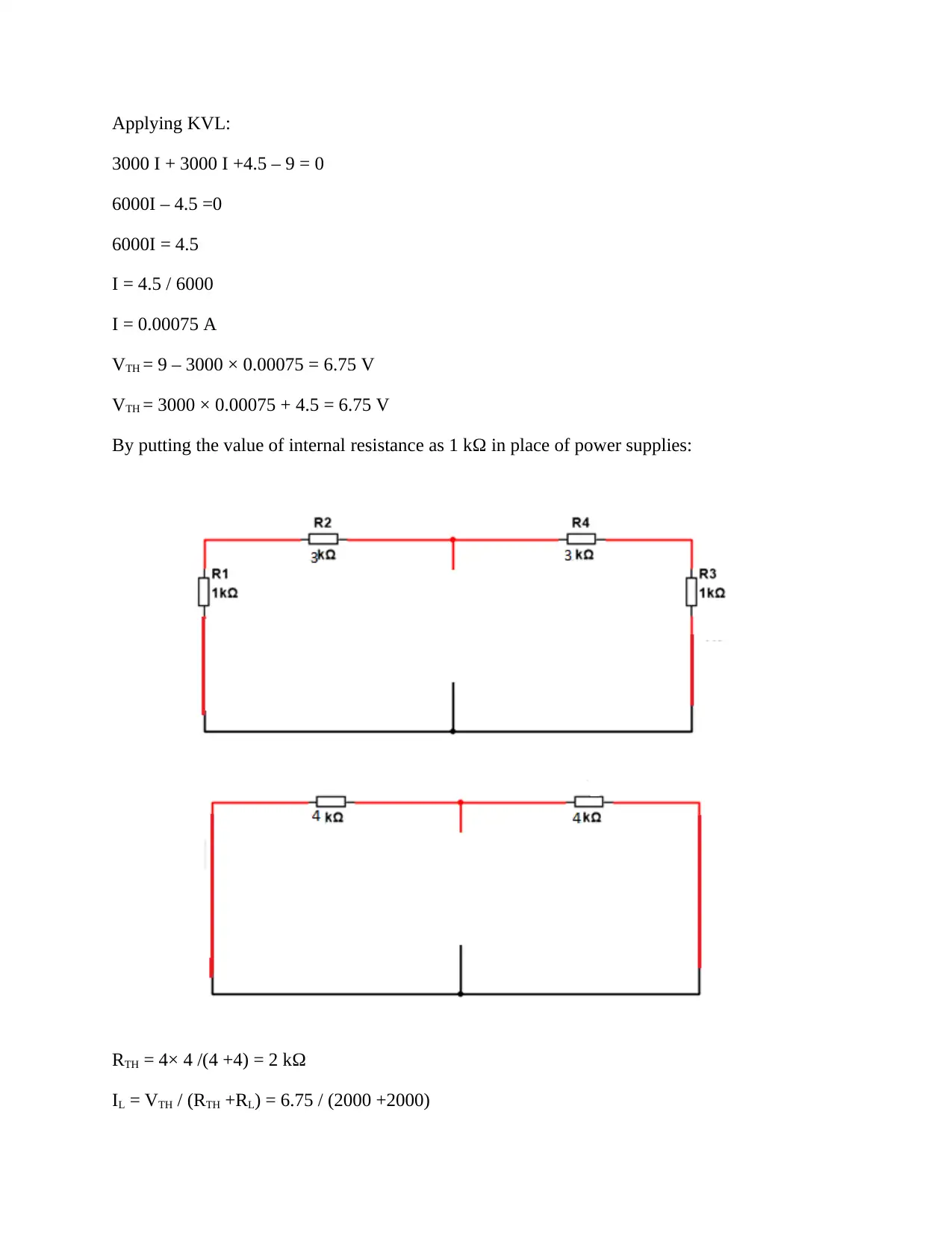
Applying KVL:
3000 I + 3000 I +4.5 – 9 = 0
6000I – 4.5 =0
6000I = 4.5
I = 4.5 / 6000
I = 0.00075 A
VTH = 9 – 3000 × 0.00075 = 6.75 V
VTH = 3000 × 0.00075 + 4.5 = 6.75 V
By putting the value of internal resistance as 1 kΩ in place of power supplies:
RTH = 4× 4 /(4 +4) = 2 kΩ
IL = VTH / (RTH +RL) = 6.75 / (2000 +2000)
3000 I + 3000 I +4.5 – 9 = 0
6000I – 4.5 =0
6000I = 4.5
I = 4.5 / 6000
I = 0.00075 A
VTH = 9 – 3000 × 0.00075 = 6.75 V
VTH = 3000 × 0.00075 + 4.5 = 6.75 V
By putting the value of internal resistance as 1 kΩ in place of power supplies:
RTH = 4× 4 /(4 +4) = 2 kΩ
IL = VTH / (RTH +RL) = 6.75 / (2000 +2000)
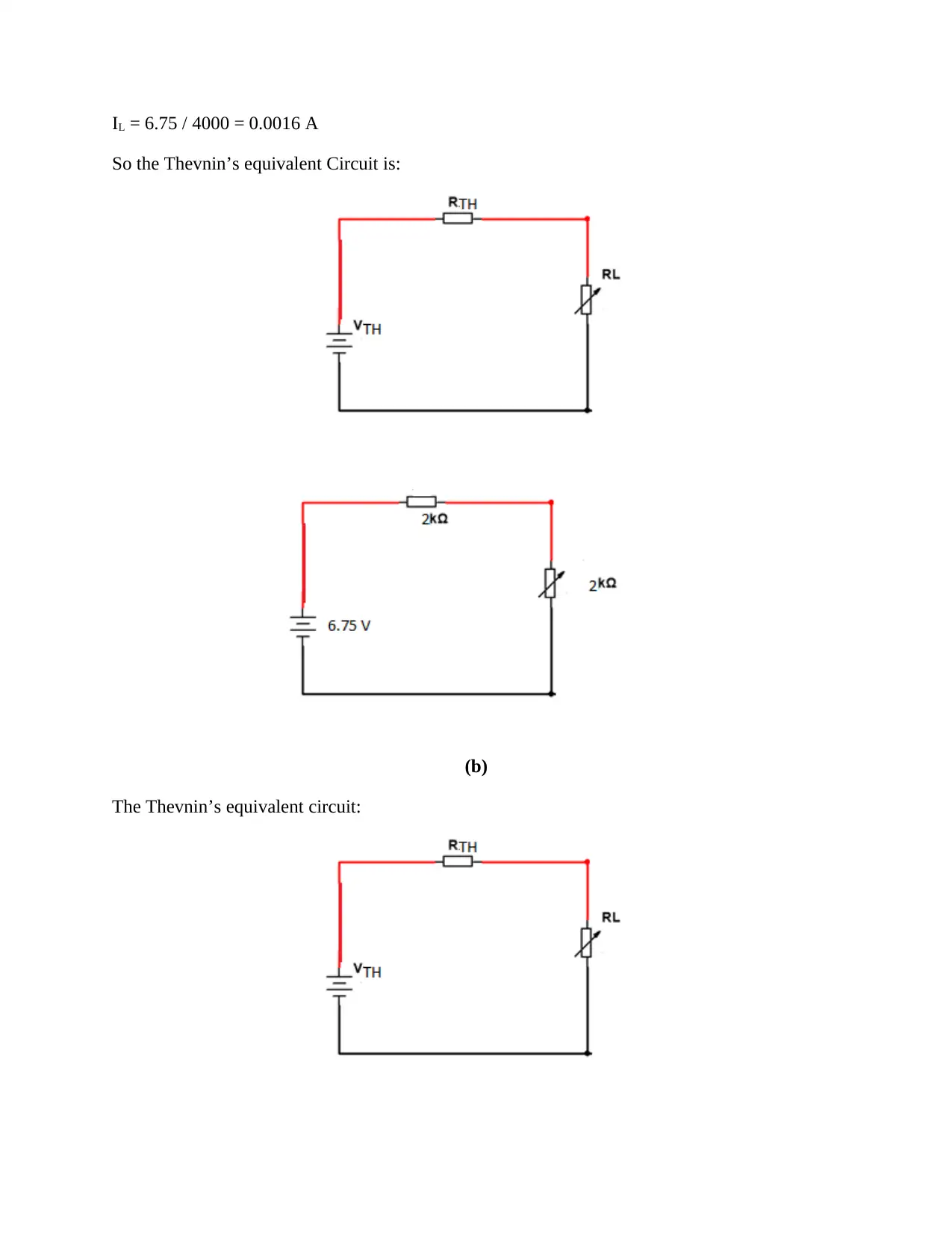
IL = 6.75 / 4000 = 0.0016 A
So the Thevnin’s equivalent Circuit is:
(b)
The Thevnin’s equivalent circuit:
So the Thevnin’s equivalent Circuit is:
(b)
The Thevnin’s equivalent circuit:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

For RL = 1KΩ,
IL = VTH / (RTH + RL) = 6.75 / (2000 +1000) = 0.0022 A
PL = IL2. RL
PL = (0.0022) 2. (1000) = 0.0050 W.
For RL = 1.5 KΩ,
IL = VTH / (RTH + RL) = 6.75 / (2000 +1500) = 0.0019A
PL = IL2. RL
PL = (0.0019) 2. (1500) = 0.0054 W.
For RL = 2 KΩ,
IL = VTH / (RTH + RL) = 6.75 / (2000 +2000) = 0.0016A
PL = IL2. RL
PL = (0.0016) 2. (2000) = 0.0051 W.
For RL = 2.5 KΩ,
IL = VTH / (RTH + RL) = 6.75 / (2000 +2500) = 0.0015A
PL = IL2. RL
PL = (0.0015) 2. (2500) = 0.0056 W.
(c)
According to Maximum Power Transfer Theorem:
For RL = 1 KΩ,
PMAX = (6.75)2 / (4 × 1000) = 0.0113 W
For RL = 1.5 KΩ,
PMAX = (6.75)2 / (4 × 1500) = 0.0075 W
For RL = 2 KΩ,
PMAX = (6.75)2 / (4 × 2000) = 0.0056 W
For RL = 2.5 KΩ,
IL = VTH / (RTH + RL) = 6.75 / (2000 +1000) = 0.0022 A
PL = IL2. RL
PL = (0.0022) 2. (1000) = 0.0050 W.
For RL = 1.5 KΩ,
IL = VTH / (RTH + RL) = 6.75 / (2000 +1500) = 0.0019A
PL = IL2. RL
PL = (0.0019) 2. (1500) = 0.0054 W.
For RL = 2 KΩ,
IL = VTH / (RTH + RL) = 6.75 / (2000 +2000) = 0.0016A
PL = IL2. RL
PL = (0.0016) 2. (2000) = 0.0051 W.
For RL = 2.5 KΩ,
IL = VTH / (RTH + RL) = 6.75 / (2000 +2500) = 0.0015A
PL = IL2. RL
PL = (0.0015) 2. (2500) = 0.0056 W.
(c)
According to Maximum Power Transfer Theorem:
For RL = 1 KΩ,
PMAX = (6.75)2 / (4 × 1000) = 0.0113 W
For RL = 1.5 KΩ,
PMAX = (6.75)2 / (4 × 1500) = 0.0075 W
For RL = 2 KΩ,
PMAX = (6.75)2 / (4 × 2000) = 0.0056 W
For RL = 2.5 KΩ,

PMAX = (6.75)2 / (4 × 2500) = 0.0045 W
So, RL = 1 KΩ that provides Maximum Power Transfer.
So, RL = 1 KΩ that provides Maximum Power Transfer.
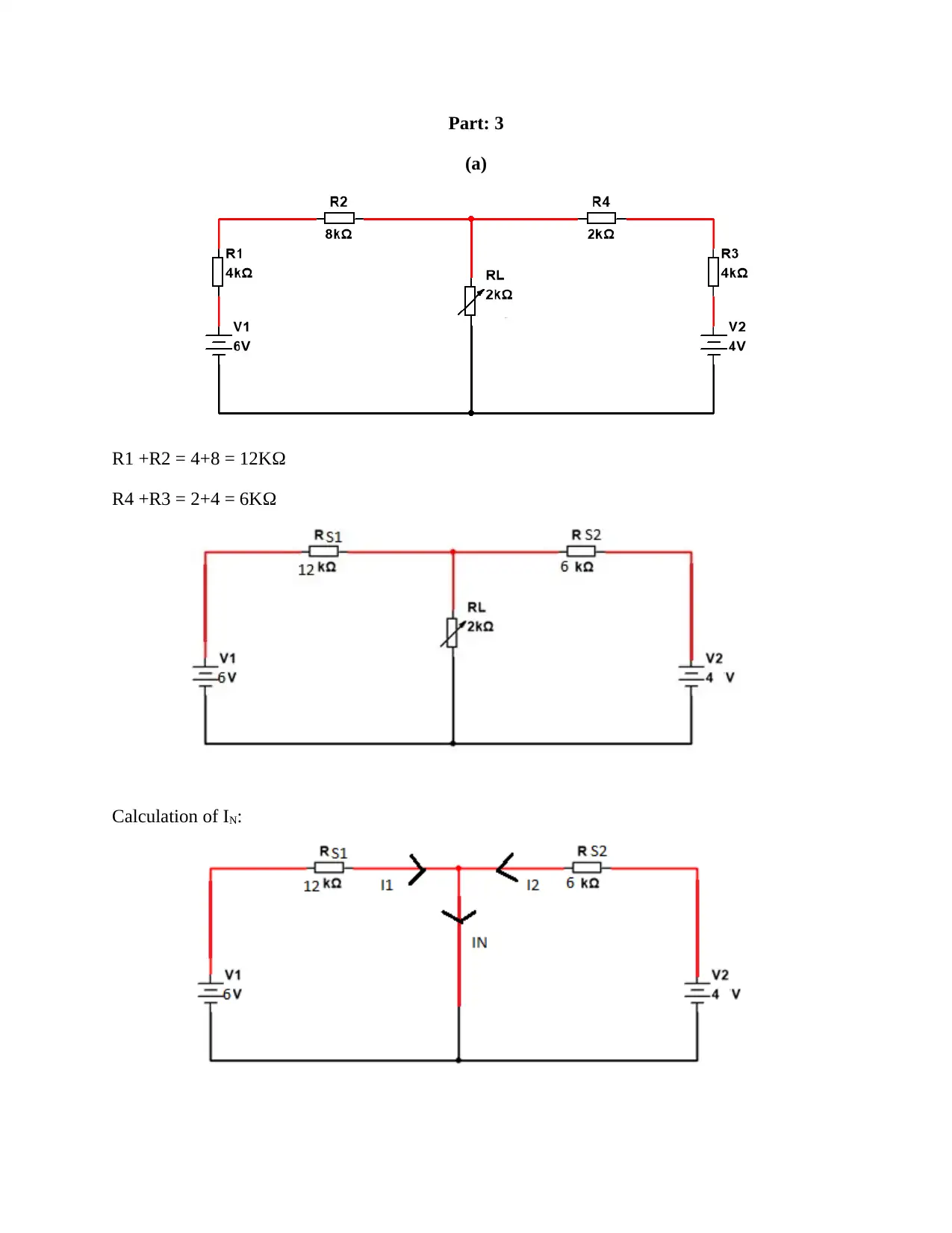
Part: 3
(a)
R1 +R2 = 4+8 = 12KΩ
R4 +R3 = 2+4 = 6KΩ
Calculation of IN:
(a)
R1 +R2 = 4+8 = 12KΩ
R4 +R3 = 2+4 = 6KΩ
Calculation of IN:
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
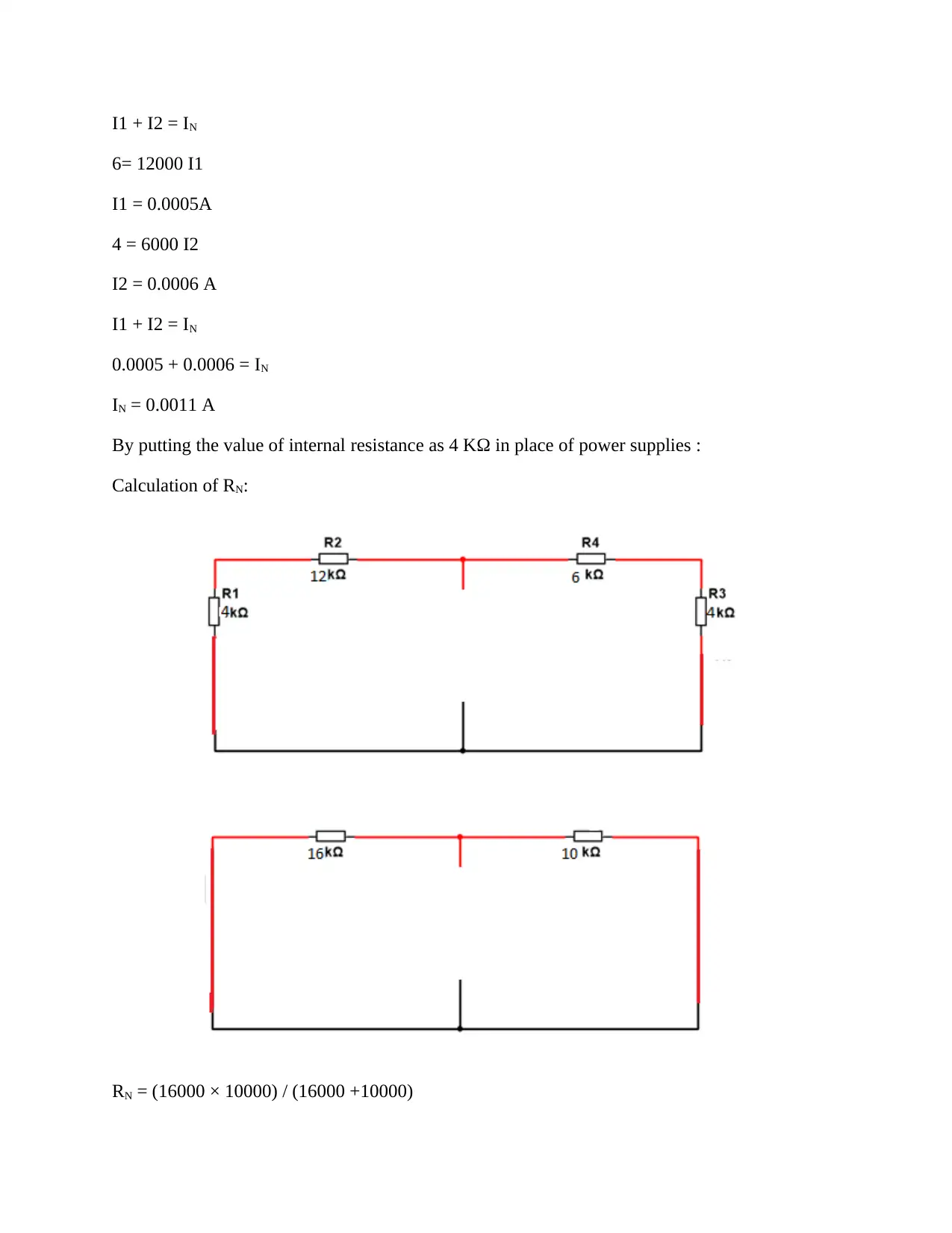
I1 + I2 = IN
6= 12000 I1
I1 = 0.0005A
4 = 6000 I2
I2 = 0.0006 A
I1 + I2 = IN
0.0005 + 0.0006 = IN
IN = 0.0011 A
By putting the value of internal resistance as 4 KΩ in place of power supplies :
Calculation of RN:
RN = (16000 × 10000) / (16000 +10000)
6= 12000 I1
I1 = 0.0005A
4 = 6000 I2
I2 = 0.0006 A
I1 + I2 = IN
0.0005 + 0.0006 = IN
IN = 0.0011 A
By putting the value of internal resistance as 4 KΩ in place of power supplies :
Calculation of RN:
RN = (16000 × 10000) / (16000 +10000)

RN = 6153.84 Ω
RN = 6.153KΩ
IL = RN / (RN + RL)
IL = 6153.84/ (6153.84 + 2000)
IL = 0.75 A
(b)
The power dissipation in the load:
For RL = 1KΩ,
IL = RN / (RN + RL)
IL = 6153.84/ (6153.84 + 1000)
RN = 6.153KΩ
IL = RN / (RN + RL)
IL = 6153.84/ (6153.84 + 2000)
IL = 0.75 A
(b)
The power dissipation in the load:
For RL = 1KΩ,
IL = RN / (RN + RL)
IL = 6153.84/ (6153.84 + 1000)

IL = 0.86 A
PL = IL2. RL
PL = (0.86) 2. (1000) = 739.6 W.
For RL = 1.5 KΩ,
IL = RN / (RN + RL)
IL = 6153.84/ (6153.84 + 1500)
IL = 0.80A
PL = IL2. RL
PL = (0.80) 2. (1500) = 960 W.
For RL = 2 KΩ,
IL = RN / (RN + RL)
IL = 6153.84/ (6153.84 + 2000)
IL = 0.75 A
PL = IL2. RL
PL = (0.75) 2. (2000) = 1125W.
For RL = 2.5 KΩ,
IL = RN / (RN + RL)
IL = 6153.84/ (6153.84 + 2500)
IL = 0.71 A
PL = IL2. RL
PL = (0.71) 2. (2500) = 1260.25W.
PL = IL2. RL
PL = (0.86) 2. (1000) = 739.6 W.
For RL = 1.5 KΩ,
IL = RN / (RN + RL)
IL = 6153.84/ (6153.84 + 1500)
IL = 0.80A
PL = IL2. RL
PL = (0.80) 2. (1500) = 960 W.
For RL = 2 KΩ,
IL = RN / (RN + RL)
IL = 6153.84/ (6153.84 + 2000)
IL = 0.75 A
PL = IL2. RL
PL = (0.75) 2. (2000) = 1125W.
For RL = 2.5 KΩ,
IL = RN / (RN + RL)
IL = 6153.84/ (6153.84 + 2500)
IL = 0.71 A
PL = IL2. RL
PL = (0.71) 2. (2500) = 1260.25W.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
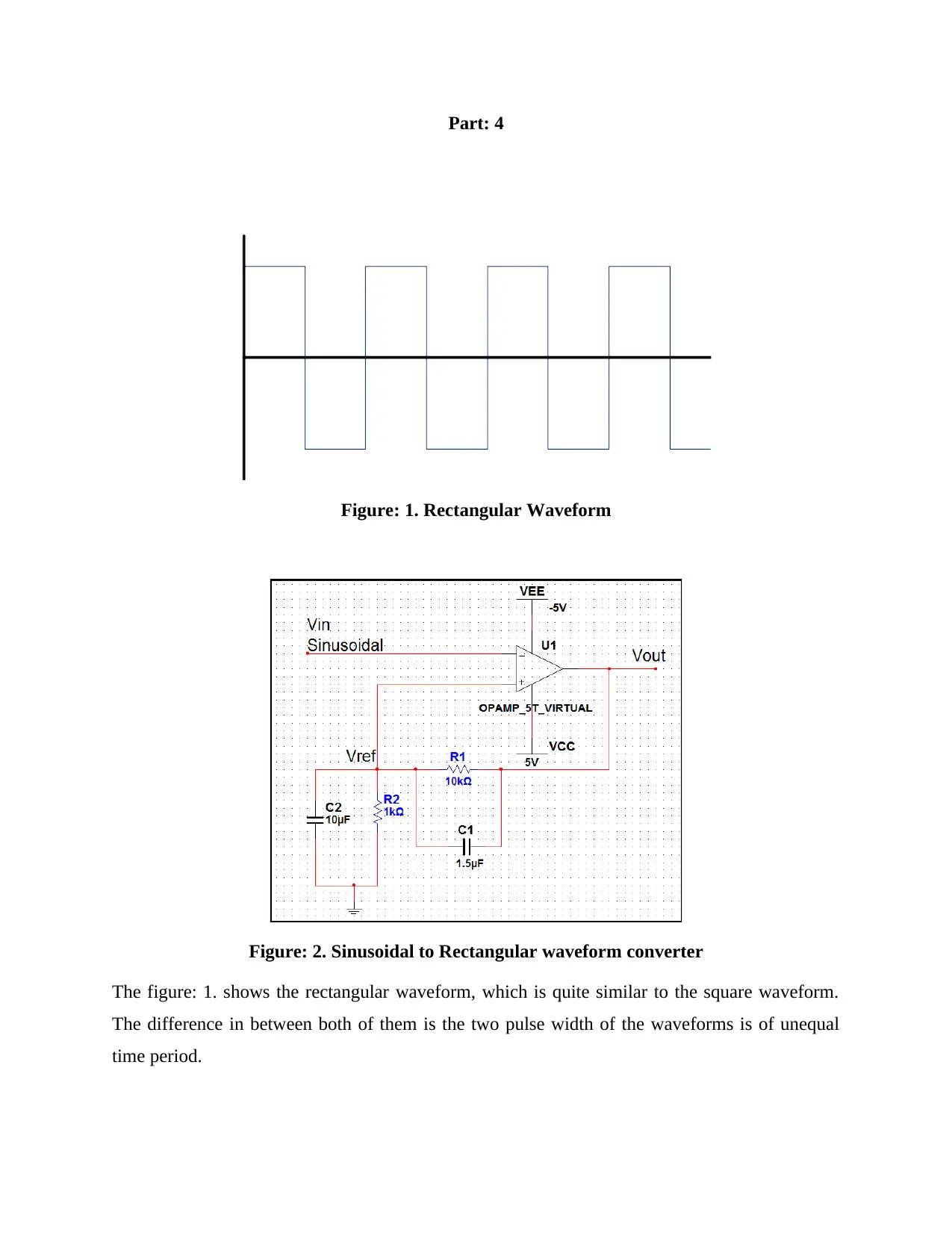
Part: 4
Figure: 1. Rectangular Waveform
Figure: 2. Sinusoidal to Rectangular waveform converter
The figure: 1. shows the rectangular waveform, which is quite similar to the square waveform.
The difference in between both of them is the two pulse width of the waveforms is of unequal
time period.
Figure: 1. Rectangular Waveform
Figure: 2. Sinusoidal to Rectangular waveform converter
The figure: 1. shows the rectangular waveform, which is quite similar to the square waveform.
The difference in between both of them is the two pulse width of the waveforms is of unequal
time period.

The above figure shows the sine to rectangular wave form conversion circuit. The input sine
signal should be enough large for passing through both of the tripping voltage for proper
conversion of sinusoidal waveform to rectangular waveform.
Any shape at input which is passes through the Schmitt trigger circuit always produce the
rectangular waveform. if the input signal is periodic. Capacitor C1 connected in parallelism
manner with R1 in practical formation as shown in Figure 2. The stray capacitor C2 and the
resistance R2 form a bypass capacitor. The effect of stray capacitance C2 can be eliminated by
the speed –up capacitor C1 across the resistor R1.The stray capacitor C2 is required to be
charged before applying at the non- inverting input voltage changes, in the absence of speed-up
capacitor. The speed-up capacitor is used to supply the necessary charge to C2; the minimum
value of speed-up capacitor must be in the calculation given below for neutralizing the effect of
stray capacitance
C1 (MIN) = (R2/R1) C2
signal should be enough large for passing through both of the tripping voltage for proper
conversion of sinusoidal waveform to rectangular waveform.
Any shape at input which is passes through the Schmitt trigger circuit always produce the
rectangular waveform. if the input signal is periodic. Capacitor C1 connected in parallelism
manner with R1 in practical formation as shown in Figure 2. The stray capacitor C2 and the
resistance R2 form a bypass capacitor. The effect of stray capacitance C2 can be eliminated by
the speed –up capacitor C1 across the resistor R1.The stray capacitor C2 is required to be
charged before applying at the non- inverting input voltage changes, in the absence of speed-up
capacitor. The speed-up capacitor is used to supply the necessary charge to C2; the minimum
value of speed-up capacitor must be in the calculation given below for neutralizing the effect of
stray capacitance
C1 (MIN) = (R2/R1) C2
Part: 5
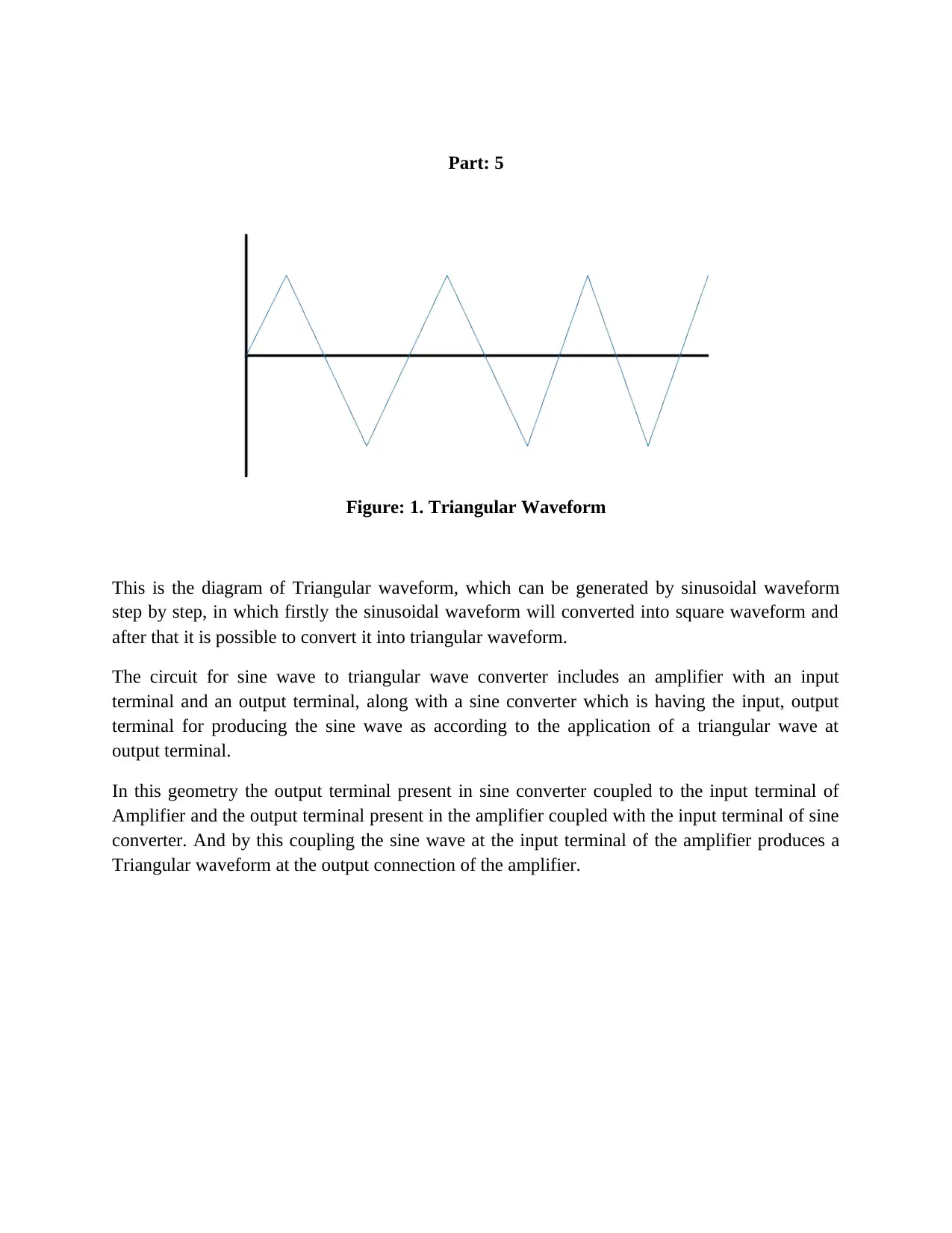
Figure: 1. Triangular Waveform
This is the diagram of Triangular waveform, which can be generated by sinusoidal waveform
step by step, in which firstly the sinusoidal waveform will converted into square waveform and
after that it is possible to convert it into triangular waveform.
The circuit for sine wave to triangular wave converter includes an amplifier with an input
terminal and an output terminal, along with a sine converter which is having the input, output
terminal for producing the sine wave as according to the application of a triangular wave at
output terminal.
In this geometry the output terminal present in sine converter coupled to the input terminal of
Amplifier and the output terminal present in the amplifier coupled with the input terminal of sine
converter. And by this coupling the sine wave at the input terminal of the amplifier produces a
Triangular waveform at the output connection of the amplifier.
Figure: 1. Triangular Waveform
This is the diagram of Triangular waveform, which can be generated by sinusoidal waveform
step by step, in which firstly the sinusoidal waveform will converted into square waveform and
after that it is possible to convert it into triangular waveform.
The circuit for sine wave to triangular wave converter includes an amplifier with an input
terminal and an output terminal, along with a sine converter which is having the input, output
terminal for producing the sine wave as according to the application of a triangular wave at
output terminal.
In this geometry the output terminal present in sine converter coupled to the input terminal of
Amplifier and the output terminal present in the amplifier coupled with the input terminal of sine
converter. And by this coupling the sine wave at the input terminal of the amplifier produces a
Triangular waveform at the output connection of the amplifier.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
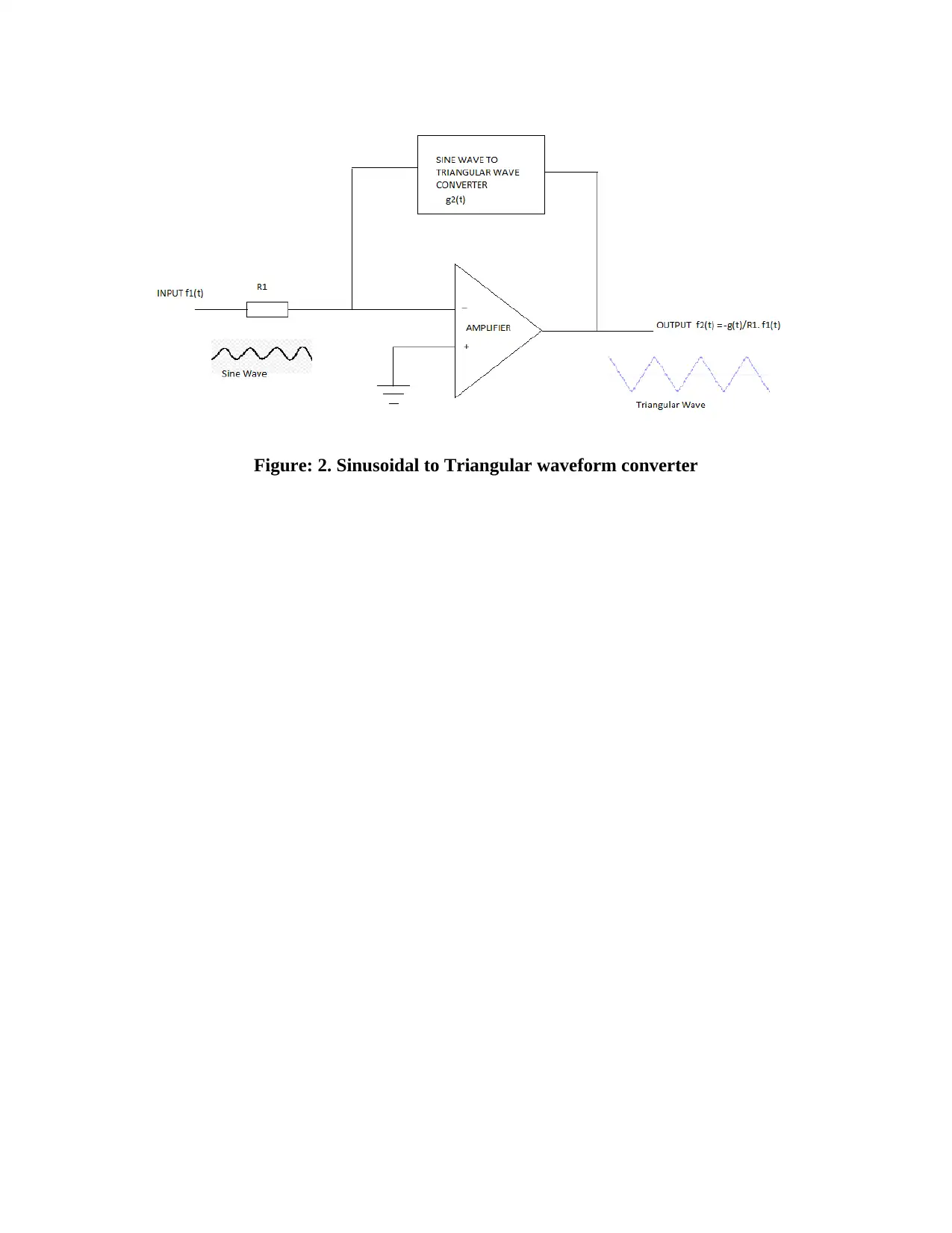
Figure: 2. Sinusoidal to Triangular waveform converter

Part: 6
A. Whether this is a high-pass, low pass or band pass filter :
This is the circuit of Low Pass filter. That is the filter which passes the lower frequency
than the selected cut-off frequency and also it attenuates the higher frequencies which
is higher than the cut- off frequency. Depending upon the filter design the exact
frequency response can be determined. And this filter is also known as High- cut filter.
B. The reactance of the capacitor at the frequency shown, Xc:
XC = 1
2 πfC
XC = 1
2 π ×500 ×0.1 ×10−6
XC = 1
2 π ×500 ×0.1 ×10−6
XC = 3183.09886184Ω
C. The impedance of the circuit at the frequency shown, Z :
Z = √ ¿2 + XC2)
A. Whether this is a high-pass, low pass or band pass filter :
This is the circuit of Low Pass filter. That is the filter which passes the lower frequency
than the selected cut-off frequency and also it attenuates the higher frequencies which
is higher than the cut- off frequency. Depending upon the filter design the exact
frequency response can be determined. And this filter is also known as High- cut filter.
B. The reactance of the capacitor at the frequency shown, Xc:
XC = 1
2 πfC
XC = 1
2 π ×500 ×0.1 ×10−6
XC = 1
2 π ×500 ×0.1 ×10−6
XC = 3183.09886184Ω
C. The impedance of the circuit at the frequency shown, Z :
Z = √ ¿2 + XC2)

Z = √ ¿2 + (3183.09)2)
Z = √ 2250000+ 10132061.9481
Z = √12382061.9481
Z = 3518.81541715Ω
D. The current in the circuit at the frequency shown, I :
Z = 3518.81541715Ω
V= I. R
I = V/ Z = 12/ 3518.81 = 0.0034 A
E. The voltage drop across the resistor at the frequency shown, VR :
VR = I. R = 0.0034 × 1500 = 5.1 V
F. The voltage drop across the capacitor at the frequency shown, Vc :
VC = I. XC = 0.0034 ×3183.09 = 10.82 V
G. The gain of the circuit at the frequency shown :
Gain in dB = 20 log (VOUT / VIN)
VOUT = VIN. XC / Z
VOUT = 12× 3183.09
3581.81
VOUT = 10.85V
Gain = -0.8750dB
Z = √ 2250000+ 10132061.9481
Z = √12382061.9481
Z = 3518.81541715Ω
D. The current in the circuit at the frequency shown, I :
Z = 3518.81541715Ω
V= I. R
I = V/ Z = 12/ 3518.81 = 0.0034 A
E. The voltage drop across the resistor at the frequency shown, VR :
VR = I. R = 0.0034 × 1500 = 5.1 V
F. The voltage drop across the capacitor at the frequency shown, Vc :
VC = I. XC = 0.0034 ×3183.09 = 10.82 V
G. The gain of the circuit at the frequency shown :
Gain in dB = 20 log (VOUT / VIN)
VOUT = VIN. XC / Z
VOUT = 12× 3183.09
3581.81
VOUT = 10.85V
Gain = -0.8750dB
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Part: 7
A. The reactance of the capacitor at the frequency shown, XC :
XC = 1
2 πfc
XC = 1
2 π ×250 ×2.2 ×10−6
XC = 289.85Ω
B. The reactance of the inductor at the frequency shown, XL :
XL = ωL
XC = 2 πf L
XC = 2 π ×250×0.29
XL= 455.53 Ω
C. The impedance of the circuit at the frequency shown, Z :
Z = √ ¿2 + (XL-XC)2)
Z = √ ¿2 + (455.53-289.85)2)
Z = 5597.54
D. The resultant phase angle of the current relative to the supply voltage at the frequency
shown,
:
A. The reactance of the capacitor at the frequency shown, XC :
XC = 1
2 πfc
XC = 1
2 π ×250 ×2.2 ×10−6
XC = 289.85Ω
B. The reactance of the inductor at the frequency shown, XL :
XL = ωL
XC = 2 πf L
XC = 2 π ×250×0.29
XL= 455.53 Ω
C. The impedance of the circuit at the frequency shown, Z :
Z = √ ¿2 + (XL-XC)2)
Z = √ ¿2 + (455.53-289.85)2)
Z = 5597.54
D. The resultant phase angle of the current relative to the supply voltage at the frequency
shown,
:

Ø = tan−1 (( ¿ X L−X C)/ R)¿
Ø = tan−1 (( ¿ 455.53−298.85)/5600)¿
Ø = 0.02950
E. The current flowing in the circuit at the frequency shown, I :
I = V
√¿ ¿ ¿ ¿
I = V
√ ¿ ¿ ¿ ¿
I = 0.0089 A
F. The voltage drop across the resistor at the frequency shown, VR :
VR = I. R
VR = 0.0089 × 5600
VR = 49.84 V
G. The voltage drop across the capacitor at the frequency shown, VC :
VC = I × XC
VC = 0.0089 × 289.85
VC = 2.579 V
H. The voltage drop across the inductor at the frequency shown, VL :
VL = I × XL
VC = 0.0089 × 455.53
VC = 4.0542 V
I. The resonant frequency of this circuit, Fr :
Ø = tan−1 (( ¿ 455.53−298.85)/5600)¿
Ø = 0.02950
E. The current flowing in the circuit at the frequency shown, I :
I = V
√¿ ¿ ¿ ¿
I = V
√ ¿ ¿ ¿ ¿
I = 0.0089 A
F. The voltage drop across the resistor at the frequency shown, VR :
VR = I. R
VR = 0.0089 × 5600
VR = 49.84 V
G. The voltage drop across the capacitor at the frequency shown, VC :
VC = I × XC
VC = 0.0089 × 289.85
VC = 2.579 V
H. The voltage drop across the inductor at the frequency shown, VL :
VL = I × XL
VC = 0.0089 × 455.53
VC = 4.0542 V
I. The resonant frequency of this circuit, Fr :

ωr2 = 1/LC
ωr = 1/√ ¿LC)
ωr = 1
√ 0.29 ×2.2 ×10−6
ωr = 1251.95 radians.
J. The reactance of the capacitor at resonance, XC :
XC = XL
K. The reactance of the inductor at resonance, XL :
XL= XC = 455.53 Ω
L. The impedance of the circuit at the resonance, Z :
In complex form, the resonant frequency is the frequency at which the total impedance
of a series RLC circuit becomes purely “real”, that is no imaginary impedance’s exist.
This is because at resonance they are cancelled out. So the total impedance of the series
circuit becomes just the value of the resistance and therefore: Z = R.
M. The resultant phase angle of the current relative to the supply voltage at resonance,
:
tan−1=( XL−XC)
R =00
N. The current flowing in the circuit at resonance, I :
I = V/R
I = 50
5600 = 0.0089A
O. The voltage drop across the resistor at resonance, VR :
ωr = 1/√ ¿LC)
ωr = 1
√ 0.29 ×2.2 ×10−6
ωr = 1251.95 radians.
J. The reactance of the capacitor at resonance, XC :
XC = XL
K. The reactance of the inductor at resonance, XL :
XL= XC = 455.53 Ω
L. The impedance of the circuit at the resonance, Z :
In complex form, the resonant frequency is the frequency at which the total impedance
of a series RLC circuit becomes purely “real”, that is no imaginary impedance’s exist.
This is because at resonance they are cancelled out. So the total impedance of the series
circuit becomes just the value of the resistance and therefore: Z = R.
M. The resultant phase angle of the current relative to the supply voltage at resonance,
:
tan−1=( XL−XC)
R =00
N. The current flowing in the circuit at resonance, I :
I = V/R
I = 50
5600 = 0.0089A
O. The voltage drop across the resistor at resonance, VR :
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Then in a series resonance circuit as VL = -VC the resulting reactive voltages are zero
and all the supply voltage is dropped across the resistor. Therefore, VR = Vsupply and it is
for this reason that series resonance circuits are known as voltage resonance circuits,
(as opposed to parallel resonance circuits which are current resonance circuits).
VR = 50V
P. The voltage drop across the capacitor at resonance, VC :
VC = VL
Q. The voltage drop across the inductor resonance, VL :
VL = I × XL
VL = 0.0089 × 455.53
VL = 4.0542 V.
R. The Q-factor of the circuit at resonance :
Q = XL / R
Q = 455.53 / 5600
Q = 0.0813
and all the supply voltage is dropped across the resistor. Therefore, VR = Vsupply and it is
for this reason that series resonance circuits are known as voltage resonance circuits,
(as opposed to parallel resonance circuits which are current resonance circuits).
VR = 50V
P. The voltage drop across the capacitor at resonance, VC :
VC = VL
Q. The voltage drop across the inductor resonance, VL :
VL = I × XL
VL = 0.0089 × 455.53
VL = 4.0542 V.
R. The Q-factor of the circuit at resonance :
Q = XL / R
Q = 455.53 / 5600
Q = 0.0813

Part: 8
Electromagnetic Induction and its Applications
A procedure in which the conductor situated in a position and magnetic field starts varying or
conductor is in moving position and magnetic field is stationary, by which the voltage or EMF will
induced across the electrical conductor is known as electromagnetic induction.
Electromagnetic induction:
By the motion of conductor across the magnetic field or or by the change in magnetic flux, an
induction of an electromotive force is induced which is determined as Electromagnetic Induction.
This process happens at the moment when either conductor is moving across the magnetic field or
conductor is in stationary position and magnetic field keeps varying.
Michael Faraday introduced the law of electromagnetic induction by organizing the wire connection
to a gadget to observe the voltage over the circuit. So whenever the magnet with magnetic field
passes through the conductor, the voltage can measure in the circuit. (Seiger 2011)
Electromagnetic Induction and its Applications
A procedure in which the conductor situated in a position and magnetic field starts varying or
conductor is in moving position and magnetic field is stationary, by which the voltage or EMF will
induced across the electrical conductor is known as electromagnetic induction.
Electromagnetic induction:
By the motion of conductor across the magnetic field or or by the change in magnetic flux, an
induction of an electromotive force is induced which is determined as Electromagnetic Induction.
This process happens at the moment when either conductor is moving across the magnetic field or
conductor is in stationary position and magnetic field keeps varying.
Michael Faraday introduced the law of electromagnetic induction by organizing the wire connection
to a gadget to observe the voltage over the circuit. So whenever the magnet with magnetic field
passes through the conductor, the voltage can measure in the circuit. (Seiger 2011)

The benefit of the process for producing the electrical energy in a circuit by magnectic fields
utilization are no usage of batteries sources. The principle of electromagnetic induction is used in
various circuits such as: generators, transformers, and motors etc.
Figure: 1 Electromagnetic induction by Faraday’s Law
Faraday’s Law:
First law: When a conductor is situated in a varying magnetic field. The EMF starts induced
in it which is known as induced EMF. After that the induced currents starts flow in it if the
conductor determines in a closed circuit structure.
Second law: The rate in difference in flux linkage will be equalizing to the magnitude of
induced EMF.
Based on that result, the number of turns in coil or the changing magnetic field of coil will be in the
same proportion with the amount of voltage induced as Faraday’s Law,
In mathematical equation, the induced voltage will be:
utilization are no usage of batteries sources. The principle of electromagnetic induction is used in
various circuits such as: generators, transformers, and motors etc.
Figure: 1 Electromagnetic induction by Faraday’s Law
Faraday’s Law:
First law: When a conductor is situated in a varying magnetic field. The EMF starts induced
in it which is known as induced EMF. After that the induced currents starts flow in it if the
conductor determines in a closed circuit structure.
Second law: The rate in difference in flux linkage will be equalizing to the magnitude of
induced EMF.
Based on that result, the number of turns in coil or the changing magnetic field of coil will be in the
same proportion with the amount of voltage induced as Faraday’s Law,
In mathematical equation, the induced voltage will be:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

e = N × dΦ.dt
In the equation, the parameters show as:
e = induced voltage
N = number of turns in the coil
Φ = magnetic flux
t = time
Lenz’s law:
As the law of Electromagnetic induction by Faraday, the moving direction of electromagnetic field will
oppose to its cause of production, according to Lenz’s Law of Electromagnetic induction.
In Mathematical equation by Lenz’s Law:
E = -N (dΦ / dt) (volts)
Electromagnetic Induction Applications:
There are various applications in which the electromagnetic induction principle is used, some of
these are:
1. AC generator
2. Electrical Transformers
3. Magnetic Flow Meter.
Working Principle of A DC Motor:
In the equation, the parameters show as:
e = induced voltage
N = number of turns in the coil
Φ = magnetic flux
t = time
Lenz’s law:
As the law of Electromagnetic induction by Faraday, the moving direction of electromagnetic field will
oppose to its cause of production, according to Lenz’s Law of Electromagnetic induction.
In Mathematical equation by Lenz’s Law:
E = -N (dΦ / dt) (volts)
Electromagnetic Induction Applications:
There are various applications in which the electromagnetic induction principle is used, some of
these are:
1. AC generator
2. Electrical Transformers
3. Magnetic Flow Meter.
Working Principle of A DC Motor:

An electrical Appratus which converts the electrical power into the mechanical energy is known
as An electric motor. (kumar, dutt & saini 2014)
The DC Motor working principle is that, a current carrying conductor which is placed in the
magnetic field, experiences a mechanical energy worked on it. By using the Fleming’s Left
hands rule it is possible to determine the direction of force, and its Magnitude can be described
mathematically by the formula as:
F = BIL
In the equation, the parameters show as:
B = Magnetic Flux Density
I = Current
L = Length of Conductor
Figure: 2 Organizations of Magnetic Poles
as An electric motor. (kumar, dutt & saini 2014)
The DC Motor working principle is that, a current carrying conductor which is placed in the
magnetic field, experiences a mechanical energy worked on it. By using the Fleming’s Left
hands rule it is possible to determine the direction of force, and its Magnitude can be described
mathematically by the formula as:
F = BIL
In the equation, the parameters show as:
B = Magnetic Flux Density
I = Current
L = Length of Conductor
Figure: 2 Organizations of Magnetic Poles

Fleming’s Left Hand Rule:
In left hand after stretching the first finger , thumb and the second finger in perpendicular
position with each other than first finger direction represents magnetic field, the second finger
direction represents the direction of current, and the thumb direction represents the mechanical
force experienced by the conductor.
Working Principle of Generator:
Generators are generally a normally copper wire, coils of conductors which are tightly bound
with the metal core and large magnets which is mounted to turn around inside it. In this structure,
the conductor will be in the moving position towards a magnetic field; the magnetic field will
associate with electrons inside the conductor for the production of current which flows inside the
circuit.. (Laakam, Dhaoui & Sbita 2014)
In generator the armature consists of core and the conductor coil, which will connected to the
mechanical energy source’s shaft. There will be a delicate magnetic field in the iron pole shoe at
that point when the armature of generator turns start first. The voltage starts rising as the
armature turns. By the voltage regulator, little voltage is making on the winding field. (Rajput,
Upadhyaya & Asthana 2017)
The voltage introduced the strong winding current which improves the capacity of the magnetic
field. The enhancing field determines extra voltage in the Armature side. The sign of shoes at
In left hand after stretching the first finger , thumb and the second finger in perpendicular
position with each other than first finger direction represents magnetic field, the second finger
direction represents the direction of current, and the thumb direction represents the mechanical
force experienced by the conductor.
Working Principle of Generator:
Generators are generally a normally copper wire, coils of conductors which are tightly bound
with the metal core and large magnets which is mounted to turn around inside it. In this structure,
the conductor will be in the moving position towards a magnetic field; the magnetic field will
associate with electrons inside the conductor for the production of current which flows inside the
circuit.. (Laakam, Dhaoui & Sbita 2014)
In generator the armature consists of core and the conductor coil, which will connected to the
mechanical energy source’s shaft. There will be a delicate magnetic field in the iron pole shoe at
that point when the armature of generator turns start first. The voltage starts rising as the
armature turns. By the voltage regulator, little voltage is making on the winding field. (Rajput,
Upadhyaya & Asthana 2017)
The voltage introduced the strong winding current which improves the capacity of the magnetic
field. The enhancing field determines extra voltage in the Armature side. The sign of shoes at
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
this time depended upon the current flow direction in field winding. The current flow will be in
opposite signs by the wrong direction. (Grover, Kumar & Ramalla 2014)
Part: 9
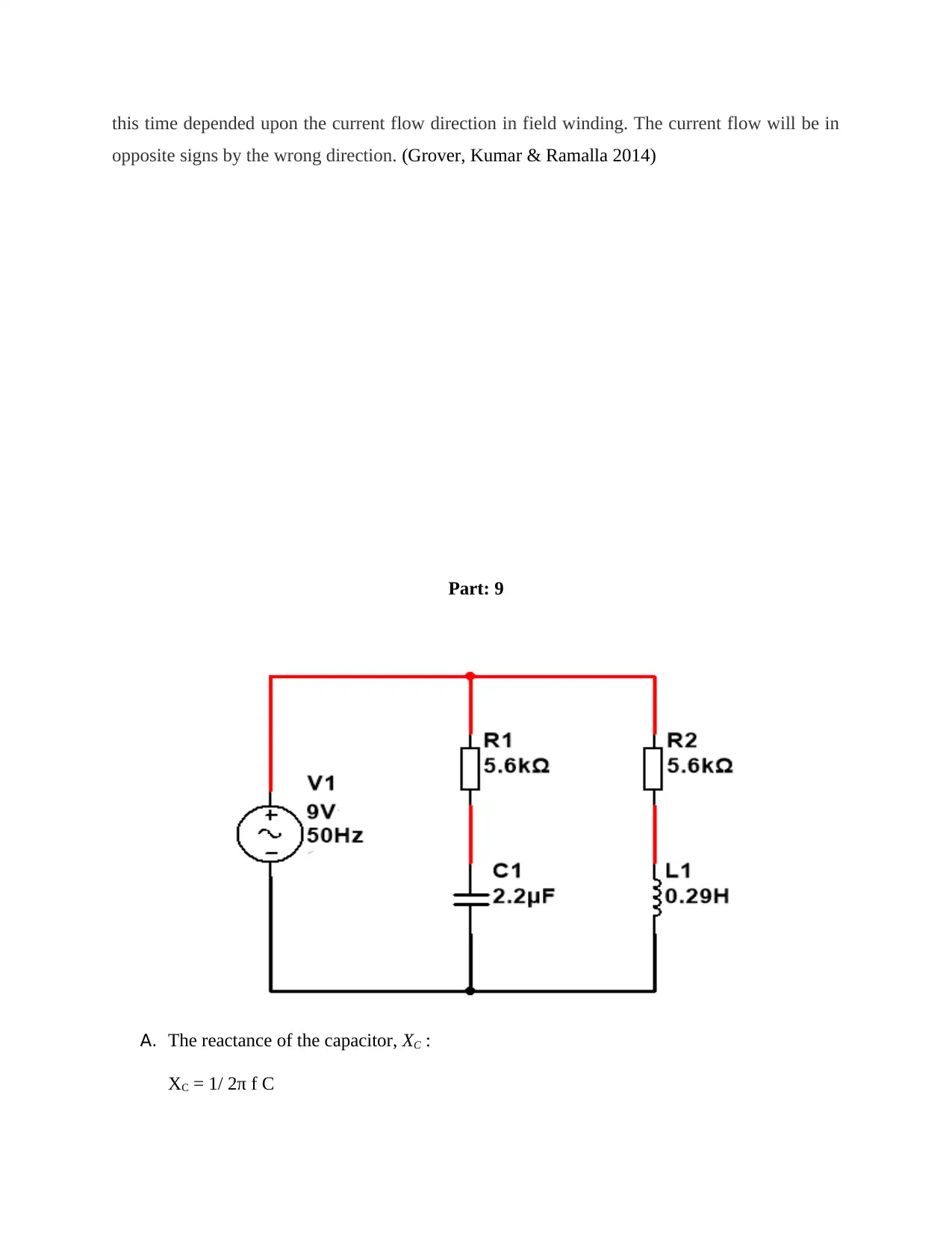
A. The reactance of the capacitor, XC :
XC = 1/ 2π f C
opposite signs by the wrong direction. (Grover, Kumar & Ramalla 2014)
Part: 9
A. The reactance of the capacitor, XC :
XC = 1/ 2π f C

XC = 1/ 2π × 50 × 2.2× 10-6
XC = 3225.80 Ω
B. The impedance of the Resistor-Capacitor branch, ZRC :
ZRC = √R2 + XC2
ZRC = √56002 + 3225.802
ZRC = 6462.64 Ω
C. The resultant phase angle of the current relative to the supply voltage in the Resistor-
Capacitor branch,
RC :RC = tan−1 Xc/ RRC = tan−1 ( 3225.80
5600 ) = 0.5226
D. The current flowing in the Resistor-Capacitor branch, IRC :
IRC = V/ ZRC
IRC = 9 / 6462.64 = 0.0013A
E. The reactance of the inductor, XL :
XL = 2π f L = 2π × 50 × 0.29 = 91.10 Ω
F. The Impedance of the Resistor-Inductor Branch, ZRL :
ZRL = √R2 + XL2
ZRL = √ 56002 + 91.10 2
ZRL = 5600.74 Ω
G. The resultant phase angle of the current relative to the supply voltage in the Resistor-
Inductor branch,
RL :
XC = 3225.80 Ω
B. The impedance of the Resistor-Capacitor branch, ZRC :
ZRC = √R2 + XC2
ZRC = √56002 + 3225.802
ZRC = 6462.64 Ω
C. The resultant phase angle of the current relative to the supply voltage in the Resistor-
Capacitor branch,
RC :RC = tan−1 Xc/ RRC = tan−1 ( 3225.80
5600 ) = 0.5226
D. The current flowing in the Resistor-Capacitor branch, IRC :
IRC = V/ ZRC
IRC = 9 / 6462.64 = 0.0013A
E. The reactance of the inductor, XL :
XL = 2π f L = 2π × 50 × 0.29 = 91.10 Ω
F. The Impedance of the Resistor-Inductor Branch, ZRL :
ZRL = √R2 + XL2
ZRL = √ 56002 + 91.10 2
ZRL = 5600.74 Ω
G. The resultant phase angle of the current relative to the supply voltage in the Resistor-
Inductor branch,
RL :

tan∅ = XL / R
tan∅ = 91.10 / 5600
tan∅ = 0.0162
H. The current flowing in the Resistor-Inductor Branch, IRL :
I = V/ ZRL
I = 9/ 5600.74 = 0.0016 A
I. The resultant current of the circuit flowing from the supply, I :
I = V/ Z = 9 / 3000.44 = 0.0029A
J. The total impedance of the circuit, Z :
Z = ZRL. ZRC /(ZRL + ZRC)
Z =5600.74 × 6462.64 / (5600.74 + 6462.64)
Z = 3000.44 Ω
tan∅ = 91.10 / 5600
tan∅ = 0.0162
H. The current flowing in the Resistor-Inductor Branch, IRL :
I = V/ ZRL
I = 9/ 5600.74 = 0.0016 A
I. The resultant current of the circuit flowing from the supply, I :
I = V/ Z = 9 / 3000.44 = 0.0029A
J. The total impedance of the circuit, Z :
Z = ZRL. ZRC /(ZRL + ZRC)
Z =5600.74 × 6462.64 / (5600.74 + 6462.64)
Z = 3000.44 Ω
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

REFERENCES
Mukhituly, M. (2016). LAWS OR EQUALITY. International Journal of Education and
Research. 4(1). pp. 203-210. Available from https://www.ijern.com/journal/2016/January-
2016/17.pdf [Accessed on 12 september 2019. ]
Seiger, H. (2011). The ScientificWorld Journal. The Confluence of Faraday’s and Kirchoff’s
Laws in Bioelectrochemical Systems. 2012(838756). pp. 1-3. Available from
https://www.hindawi.com/journals/tswj/2012/838756/ [Accessed on 13 september 2019. ]
Rajput, P., Upadhyaya, H. and Asthana, D. (2017). International Research Journal of
Engineering and Technology (IRJET). Free Energy Generator. 4(4). pp. 1832-1834. Available
from https://www.irjet.net/archives/V4/i4/IRJET-V4I4382.pdf [Accessed on 13 september
2019. ]
Grover, M., Kumar, B. and Ramalla, I. (2014). International Journal of Scientific and Research
Publications,. The Free Energy Generator. 4(12). pp. 1-4. Available from www.ijsrp.org
[Accessed on 13 september 2019. ]
Kumar, A., Dutt, A. and Saini, G. (2014). Single Phase Induction Motor. International Journal
of Research (IJR). 1(11). pp. 39-43. Available from
https://pdfs.semanticscholar.org/32db/368d213209d4841537dc4d0ac79fcda0637f.pdf [Accessed
on 13 september 2019. ]
Laakam, M., Dhaoui, M. and Sbita, L. (2014). STUDY OF INDUCTION GENERATOR
ISOLATED MODE. IJREAT International Journal of Research in Engineering & Advanced
Technology. 2(1). pp. 1-14. Available from www.ijreat.org [Accessed on 13 september 2019. ]
Mukhituly, M. (2016). LAWS OR EQUALITY. International Journal of Education and
Research. 4(1). pp. 203-210. Available from https://www.ijern.com/journal/2016/January-
2016/17.pdf [Accessed on 12 september 2019. ]
Seiger, H. (2011). The ScientificWorld Journal. The Confluence of Faraday’s and Kirchoff’s
Laws in Bioelectrochemical Systems. 2012(838756). pp. 1-3. Available from
https://www.hindawi.com/journals/tswj/2012/838756/ [Accessed on 13 september 2019. ]
Rajput, P., Upadhyaya, H. and Asthana, D. (2017). International Research Journal of
Engineering and Technology (IRJET). Free Energy Generator. 4(4). pp. 1832-1834. Available
from https://www.irjet.net/archives/V4/i4/IRJET-V4I4382.pdf [Accessed on 13 september
2019. ]
Grover, M., Kumar, B. and Ramalla, I. (2014). International Journal of Scientific and Research
Publications,. The Free Energy Generator. 4(12). pp. 1-4. Available from www.ijsrp.org
[Accessed on 13 september 2019. ]
Kumar, A., Dutt, A. and Saini, G. (2014). Single Phase Induction Motor. International Journal
of Research (IJR). 1(11). pp. 39-43. Available from
https://pdfs.semanticscholar.org/32db/368d213209d4841537dc4d0ac79fcda0637f.pdf [Accessed
on 13 september 2019. ]
Laakam, M., Dhaoui, M. and Sbita, L. (2014). STUDY OF INDUCTION GENERATOR
ISOLATED MODE. IJREAT International Journal of Research in Engineering & Advanced
Technology. 2(1). pp. 1-14. Available from www.ijreat.org [Accessed on 13 september 2019. ]

1 out of 33
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.