MATH2000 Assignment 1: Solutions to Differential Equations (18-19)

This assignment solution provides detailed, step-by-step answers to a range of problems from MATH2000 Assignment 1. It covers solving initial value problems for differential equations, including both homogeneous and non-homogeneous cases with methods like finding complementary functions and particular integrals. The solution demonstrates how to determine if an equation is exact and how to find integrating factors when it is not. It also includes the evaluation of integrals, including those involving inverse hyperbolic functions and the use of substitutions like sech(t). Furthermore, the assignment addresses double integrals, including sketching the domain of integration and evaluating iterated integrals, along with changing the order of integration where necessary. The problems cover a range of calculus and analysis techniques relevant to the course.

(1) Solve the given initial value problem
(a) y’’−6y’ + 13y = 4ex, y (0) = 2, y’ (0) = 4.
Solution:
y’’−6y’ + 13y = 4ex
D2−6D + 13 = 0
D= 6 ∓ √ 36−52
2 =3 ∓ 2 i
CF=C1e3+2i+C2e3-2i
PI= 4 e x
D2−6 D+13
D=1
PI= 4 ex
1−6+13 = ex
2
y= CF+PI= C1e3+2i+C2e3-2i+ ex
2
y (0) = 2
2=C1+C2
+ 1
2
C1+C2¿ 3
2 (1)
y’= C1 (3+2i) e3+2i+C2 (3-2i) e3-2i+ ex
2
y’ (0) = 4
y’ (0) = C1 (3+2i) +C2 (3-2i) + 1
2
C1 (3+2i) +C2 (3-2i) = 7
2 (2)
(1) × (3+2i)
C1(3+2 i)+(3+2 i)C2¿ 3
2(3+2i) (3)
equating ( 2 ) ∧(3)
we get
C2 = 1+3i
4 i

Substituting value of C2 in (2) we get
C1 (3+2i) + 1+ 3i
4 i (3-2i) = 7
2
C1 (3+2i) = 7
2 −1+3 i
4 i (3-2i)
C1 = 7
2(3+2 i) − 1+ 3i
4 i(3+2 i) (3-2i)
=
7
2 − 9
4 i− 7 i
4
(3+2 i)
= 3+i
2(3+2 i)
Hence,
y= 3+i
2(3+2 i)e(3+2i)+ 1+ 3i
4 i e3-2i+ex
2
(b) y’’−4y’ + 5y = e2x sec(x), y (0) = 1, y’ (0) = 0.
Solution:
y’’−4y’ + 5y = e2x sec(x)
D2−4D + 5 = 0
D= 4 ∓ √ 16−20
2 =2∓ i
CF=C1e(2+i) x+C2e(2-i) x
PI= e2 x sec (x )
D2−4 D+ 5
PI= e2 x sec ( x )
( D+2)2−4 ( D+2)+5
= e2 x sec(x)
D2 +1
= e2 x real part of 1
( D¿¿ 2+1)cos (x )¿
= e2 x real part of e−ix
( D¿¿ 2+1)¿
= e2 x real part of e−ix
(( D+i)¿¿ 2+1)¿

= e2 x real part of e−ix
D2−2 Di
= e2 x real part of e−ix 1
2 Di ¿
= e2 x real part of e−ix 1
2 Di [1+ D
2 i + ( D
2i )
2
+…]
= e2 x real part of e−ix (−1
2 i )∫1 dx
= e2 x real part of e−ix (−1
2 i ) x
= e2 x real part of ( cos ( x ) −isin ( x ) )(−1
2i ) x
¿ e2 x x sin ( x )
2
y= CF+PI= C1e(2+i) x+C2e(2-i) x+ e2 x x sin ( x )
2
y (0) = 1
1= C1+C2 (1)
y’ (0) = 0.
y’= (2+i) e(2+i) x+(2-i) e(2-i) x+ ¿ ¿ ¿
0= (2+i) e(2+i) x+(2-i) e(2-i) x (2)
(1) × (2+i)
(2+i) =(2+i) C1+(2+i) C2 (3)
equating ( 2 )∧(3)
we get
C2 = 2+i
2 i
Substituting value of C2 in (1) we get
C1+ 2+ i
2 i =1
C1=1- 2+ i
2 i
C1= i−2
2i

Hence,
y= i−2
2i e(2+i) x+ 2+ i
2 i e(2-i) x+ e2 x x sin ( x )
2
(2) (a) Show that any equation of the form
M’(x)N (y) + M(x)N’(y) dy
dx =0
is exact.
Show that the equation
exp ( x2 ) sin ( y2)
y + exp ( x2 ) cos ( y2 )
x
dy
dx =0
is not exact. Find a separable function T(x,y) = g(x)h(y) such that
T ( x , y ) exp ( x2 ) sin ( y2 )
y +T ( x , y ) exp ( x2 ) cos ( y2)
x
dy
dx =0
is exact and solve it.
Solution:
M’(x)N (y) + M(x)N’(y) dy
dx =0
du =M’(x)N (y) dx + M(x)N’(y)dy =0 (1)
du= ∂ u
∂ x dx += ∂u
∂ y dy (2)
∂ u
∂ x =M’(x)N (y) (3)
∂u
∂ y = M(x)N’(y) (4)
From (3) and (4)
∂(M ' ( x) N ( y ))
∂ y = ∂(M ( x) N ' ( y ))
∂ x
∂(M ' ( x) N ( y ))
∂ y = exp ( x2 ) sin ( y2)
y
=ex2 (2 y¿ ¿2 cosy 2−siny2 )
y2 ¿
∂(M (x) N ' ( y ))
∂ x = exp ( x2 ) cos ( y2 )
x

=cosy2 (2 x¿ ¿2 ex2
−ex2
)
x2 ¿
Multiplying both sides by I.F,
I.F=
e∫
∂ (M ( x)N ' (y ))
∂ x − ∂(M ' (x)N ( y))
∂ y
M ’(x)N ( y)
=
e
∫
ex2
cos y2(2 x2−1)
x2 − ex2
(2 y2 cos y2−sin y2 )
y2
ex2
sin y2
y
=
e
∫
y2 (e¿¿ x2 cos y2(2 x2−1))− x2 ex2
(2 y2 cos y2−sin y2)
x2 y2
ex2
sin y2
y
¿
=e∫( 1
y ¿− ycot y2)dy ¿
Put y2=t ;2 ydy =dt
=elogydy−log √ sint dt
= y
√sin y2
There fore, T(x,y)= y
√sin y2
(3) (a) Show that;
arcoth(x) = 1
2 ln (x +1)
( x−1),|x|>1.
Solution:
arcoth(x) = tanh-1x = 1
2 ln (x +1)
( x−1),|x|>1.
tanh-1x = y
x = tanh(y)
x = e y−e− y
e y+ e− y
( e y +e− y ¿ x = e y−e− y
x ey + x e− y = e y−e− y
x e2 y+ x
e y = e2 y −1
e y
x e2 y + x=e2 y−1

x e2 y + x−e2 y +1= 0
¿
( e2 y )=−(x+1)
(x−1)
( e2 y )= (1+ x)
(1−x)
2y = ln ( 1+x )
( 1−x )
y = 1
2ln ( 1+ x )
( 1−x )
tanh-1x = y = 1
2ln ( 1+ x )
( 1−x )
hence
arcoth(x) = tanh-1x = 1
2 ln ( x +1)
( x−1)
(b) Evaluate the integrals
∫
2
3
1
1−x2 dx ,and ∫ cosh ( √ x)
√ x dx .
Show all working.
Solution:∫
2
3
1
1−x2 dx ,= −∫
2
3
1
x2 −1 dx ,
=∫
2
3
1
( x −1)(x +1) dx
= 1
2∫
2
3
1
x−1 dx- 1
2∫
2
3
1
x +1 dx (1)
Solving 1
2∫
2
3
1
x−1 dx
Substitute u=x-1 , dx=du
= 1
2∫
1
2
1
u du
= 1
2 ln u = 1
2 ln ( x−1) (2)

Solving 1
2∫
2
3
1
x +1 dx
Substitute v=x+1 , dx=dv
= 1
2∫
1
2
1
v dv
= 1
2 ln v = 1
2 ln ( x+1) (3)
From equation we get
∫
2
3
1
1−x2 dx= 1
2 ln ( x+ 1 )− 1
2 ln ¿)
= ln ( 4 )−ln ( 3 )−ln (2)
2 = -0.2027325.
solve∫ cosh (√ x)
√ x dx .
Solution: Substitute u= √ x , dx = 2 √ x du
∫ cosh ( √x )
√ x dx =2∫ cosh ( u ) dx
¿ 2 sinh ¿)
¿ 2 sinh ¿)+C
(4) Determine the existence and uniqueness of a solution to the initial value problem
y’= cos(xy )
y √ 1−x2 , y (0) =2
Solution:
y’= cos(xy )
y √ 1−x2 , y (0) =2
f(x,y)= cos( xy )
y √ 1−x2
when x=0,y=2 apply values in f(x,y)
f(x,y)= cos( 0)
2 √ 1 = 1
2
hence f(x,y) is continuous at (0,2)

∂ f (x , y)
∂ y = ∂
∂ y ( cos ( xy )
y √ 1−x2 )
¿ 1
√1−x2
∂
∂ x
cos (xy )
y
¿ 1
√1−x2 [
−sin ( xy ) ∂ xy
∂ y . y −cos ( xy )
y2 ]
¿ 1
√ 1−x2 [−xysin ( xy ) −cos ( xy )
y2 ]
¿ −xysin ( xy ) −cos ( xy )
y2 √ 1−x2
x=0,y=2 apply values in f’(x,y)
f’(x,y) ¿ 0−cos ( 0 )
22 √ 1−0 =−1
4
hence f’(x,y) is continuous at (0,2)
Hence this equation has unique solution.
(5) Express the inverse hyperbolic secant function (usually written sech−1, arsech or arcsech) in
terms of the natural logarithm. Note that the domain is (0,1] while the range is [0,∞].
Solution:
sech (x)= 1
cosh ( x) = 2
ex+ e−x
y= sech−1 (x)
x= sech (y)= 1
cosh ¿ ¿= 2
e y+ e− y
1
x = e y+ e− y
2
0=e y +e− y− 2
x
=¿)e y
=e2 y+ e0− 2e y
x
=(e y )2−2 ( e¿¿ y )
x +1 ¿

e y= 1
x + √1−x2
x
ln (e y ¿=ln ( 1
x + √1−x2
x )
y=ln ( 1
x + √1−x2
x )
sech−1 (x)¿ ln ( 1
x + √1−x2
x )
(6) Evaluate the integral;
∫
−0.5
−0.2
1
x √ 1−x2 dx
by making a substitution involving sech(t). Use your answer to question (5) to give the final
answer correct to 4 decimal places. (Hint, why can you not make the simple substitution x =
sech(t) over this domain?)
Solution:
∫
−0.5
−0.2
1
x √ 1−x2 dx
Put x=sech (t), dx = - sech(t)tanh(t) dt
∫
−0.5
−0.2 −sech ( t) tan (t )
sech (t ) √1−sech (t)2 dt
√1−sech ( t)2=√ tanh (t)2 =tan (t )
∫
−0.5
−0.2 −sech (t )tan (t )
sech (t ) tan (t ) dt
∫−1 dt= -t =- sech-1 (x) =−ln ( 1
x + √1−x2
x )
∫
−0.5
−0.2
1
x √ 1−x2 dx=ln ( 1
−0.5 + √1−0.52
−0.5 )−ln ( 1
−0.2 + √1−0.22
−0.2 )
¿ ln (−3.73 ) −ln (−9.899 ) =ln 3.73
9.899
¿−¿0.9760
(7) Consider the double integrals;
∫
0
3 π
4
∫
1
2
er2
rdrdθand∫
0
4
∫
√ y
2
ex3
dxdy

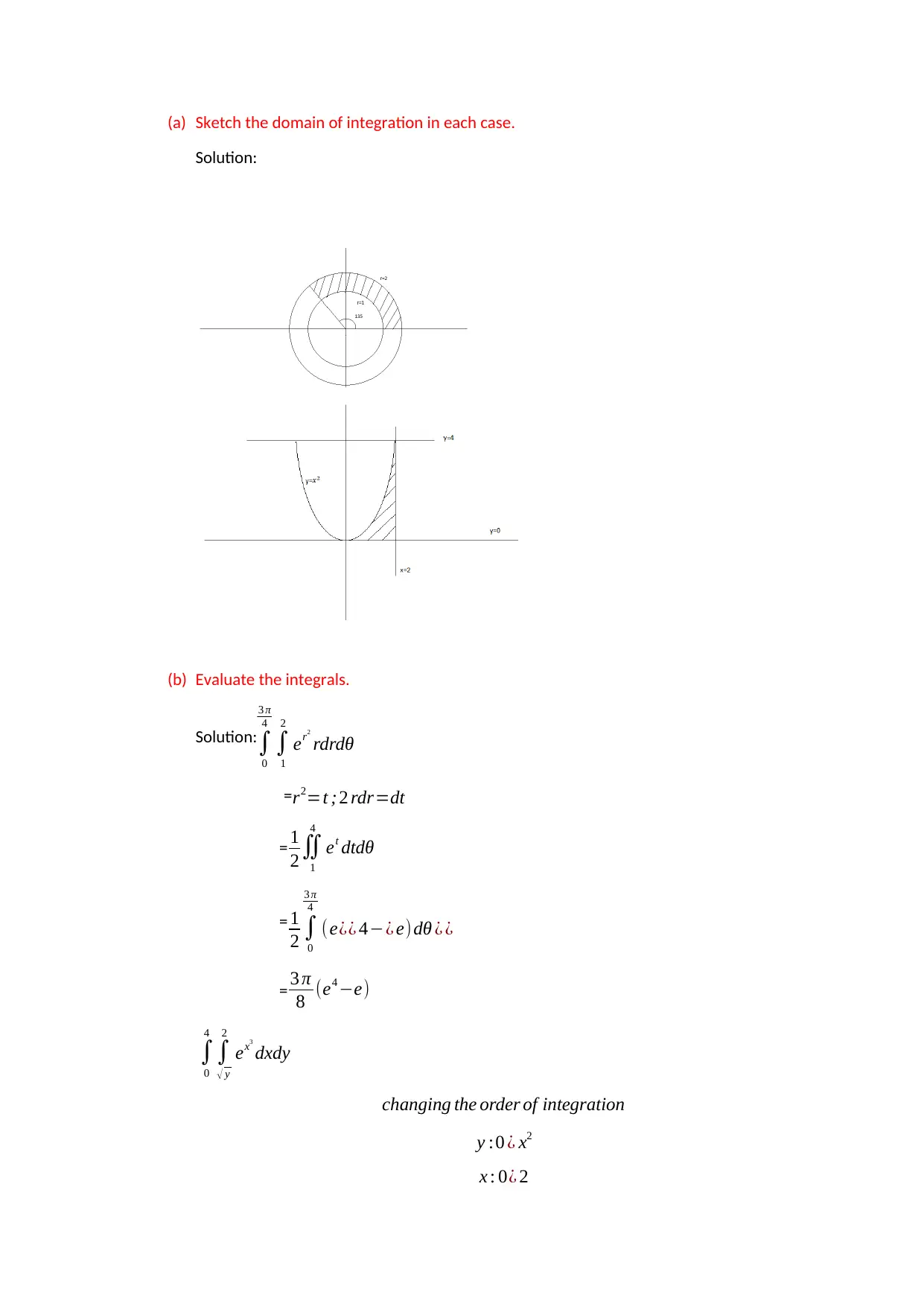
(a) Sketch the domain of integration in each case.
Solution:
(b) Evaluate the integrals.
Solution:
∫
0
3 π
4
∫
1
2
er2
rdrdθ
= r2=t ; 2 rdr=dt
= 1
2∬
1
4
et dtdθ
= 1
2 ∫
0
3 π
4
(e¿¿ 4−¿ e) dθ ¿ ¿
= 3 π
8 (e4 −e)
∫
0
4
∫
√ y
2
ex3
dxdy
changing the order of integration
y :0 ¿ x2
x : 0¿ 2

=∫
0
2
∫
0
x2
ex3
dydx
¿∫
0
2
ex3
y , 0 , x2 dx
¿∫
0
2
ex3
x2 dx; put x3=t ,3 x2 dx =dt
¿ 1
3 ∫
0
8
et dt
= 1
3 ( e8−1)
(8) Consider the expression
I= ∫
0
1
∫
0
1− z2
∫
0
z
dxdydz +∫
0
1
∫
1− z2
1
∫
0
√ 1− y
dxdydz
(a) Determine the value of I by evaluating the iterated integrals given.
Solution:
I= ∫
0
1
∫
0
1− z2
∫
0
z
dxdydz +∫
0
1
∫
1− z2
1
∫
0
√ 1− y
dxdydz
∫
0
1
∫
0
1− z2
∫
0
z
dxdydz= ∫
0
1
∫
0
1− z2
z dydz
=∫
0
1
z (1−z2 ¿) dz ¿
=∫
0
1
z2−z3 dz
= 1
2 − 1
4 = 1
4
∫
0
1
∫
1− z2
1
∫
0
√ 1− y
dxdydz=∫
0
1
∫
1− z2
1
√1− y dydz
Put 1-y =u
∫ √1− y dy =−∫ √u du
2u
3
2
3
= 2(1− y )
3
2
3

∫
0
1
∫
1− z2
1
∫
0
√ 1− y
dxdydz= 2
3 ∫
0
1
z3 dz
= 1
6
I= ∫
0
1
∫
0
1− z2
∫
0
z
dxdydz +∫
0
1
∫
1− z2
1
∫
0
√ 1− y
dxdydz = 5
12
(b) Rewrite I using the order of integration dy dx dz and evaluate the new expression.
Solution:
I= ∫
0
1
∫
0
z
∫
0
1− z2
dydxdz +∫
0
1
∫
0
√ 1− y
∫
1− z2
1
dydxdz
∫
0
1
∫
0
z
∫
0
1− z2
dydxdz = ∫
0
1
∫
0
z
(¿¿1−z2 ) dxdz ¿ ¿
= ∫
0
1
(1−z2 )z dz
=∫
0
1
z2−z3 dz
= 1
2 − 1
4 = 1
4
∫
0
1
∫
0
√ 1− y
∫
1− z2
1
dydxdz=∫
0
1
∫
0
√ 1− y
z2 dxdz
= ∫
0
1
z2 ( √ 1− y ) dz
= 1
3 √1− y
I= ∫
0
1
∫
0
z
∫
0
1− z2
dydxdz +∫
0
1
∫
0
√ 1− y
∫
1− z2
1
dydxdz = 1
4 + 1
3 √1− y
(9) Find the volume of the solid enclosed by the paraboloid z − x2 − y2 = −1 and the hemisphere
z=√ 1−x2− y2
Solution:
z − x2 − y2 = −1
x2 + y2 = z +1…………. (1)
z=√ 1−x2− y2