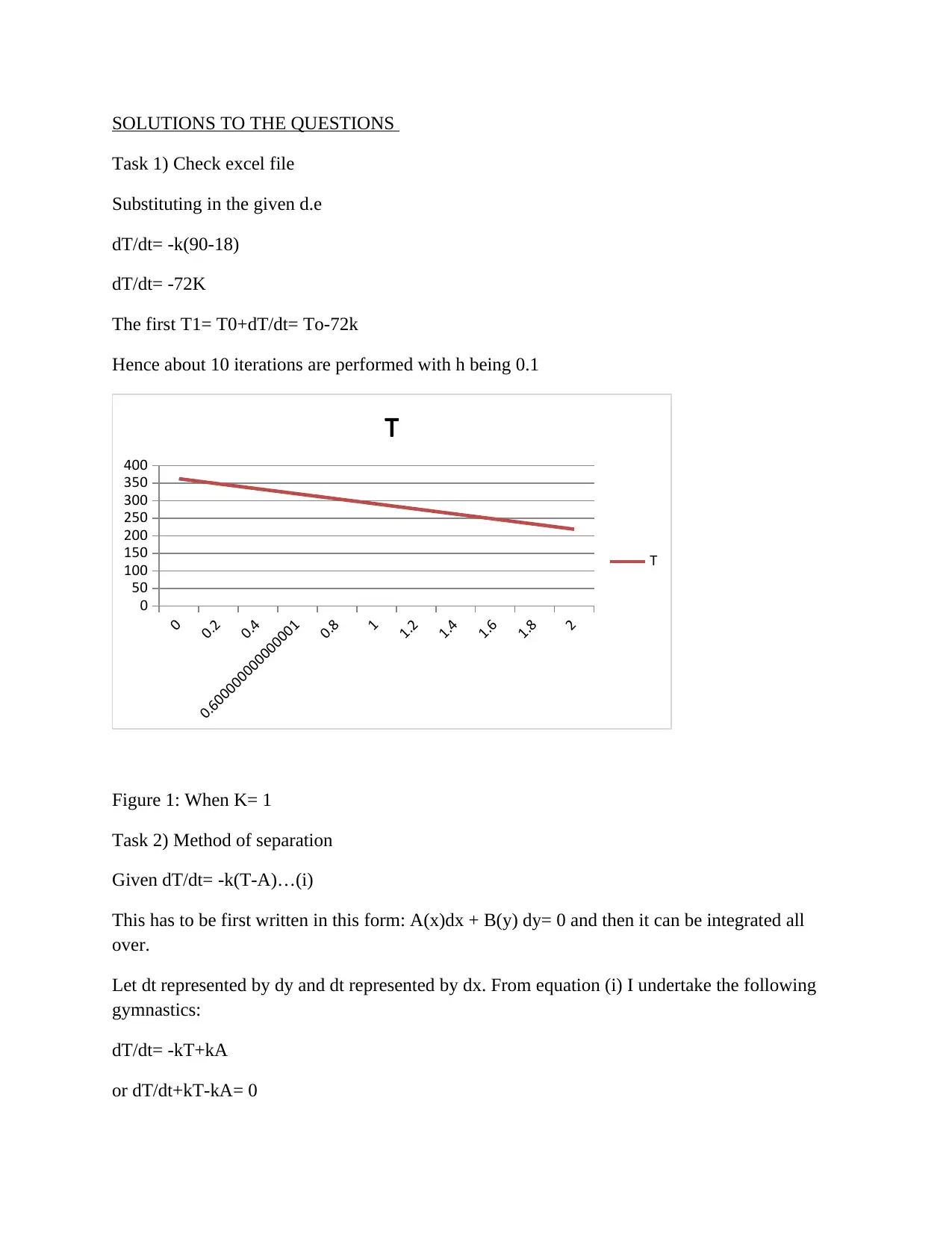
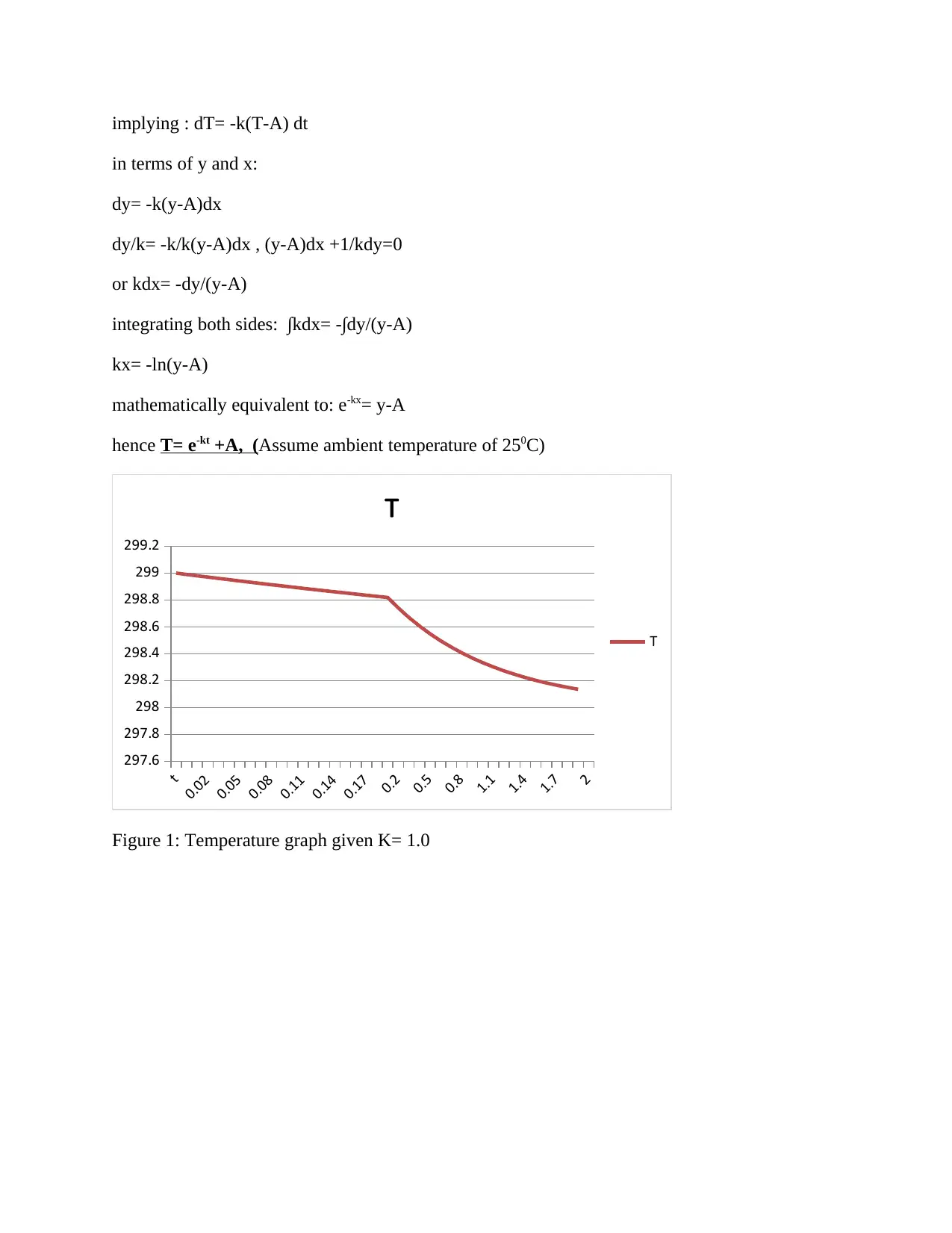
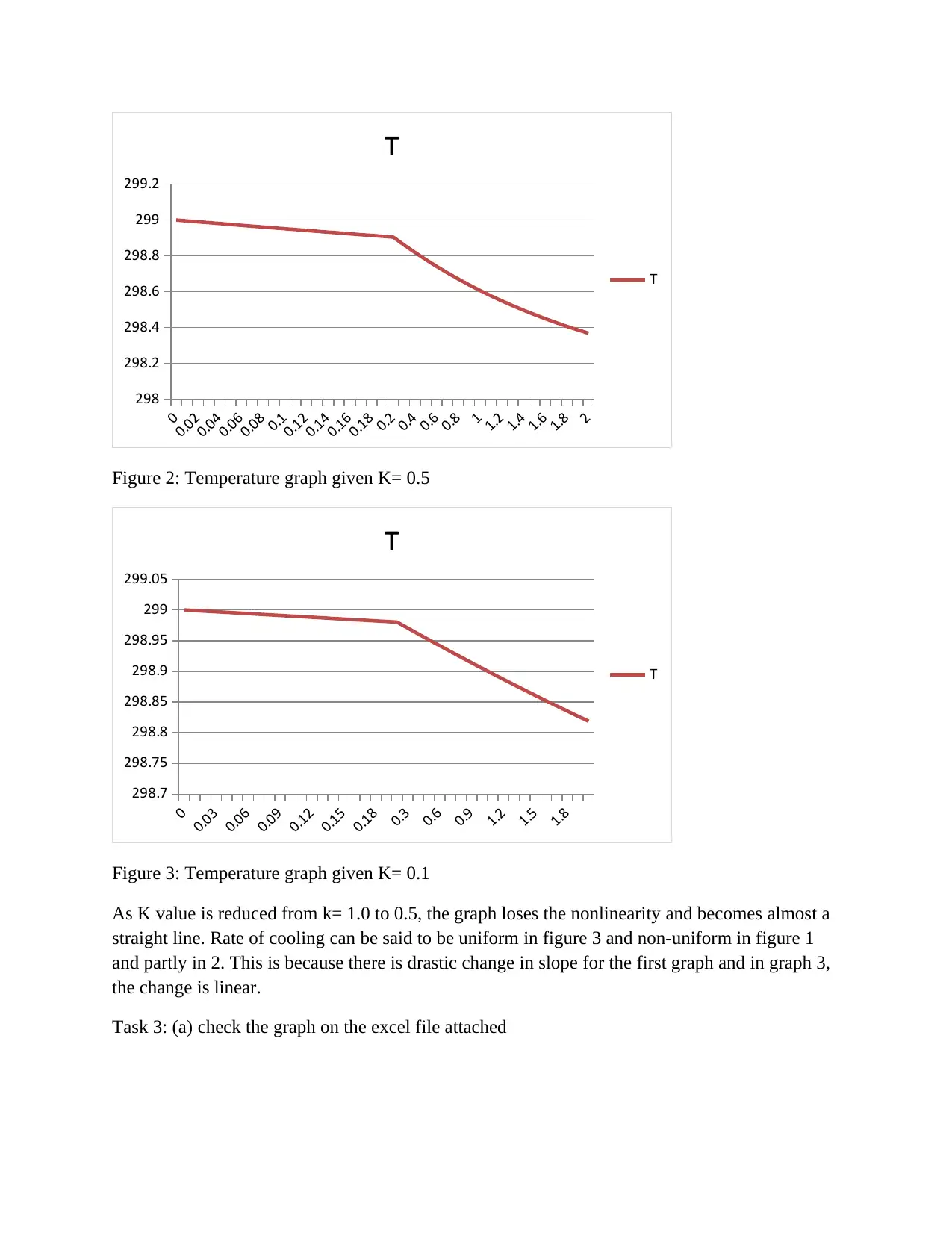
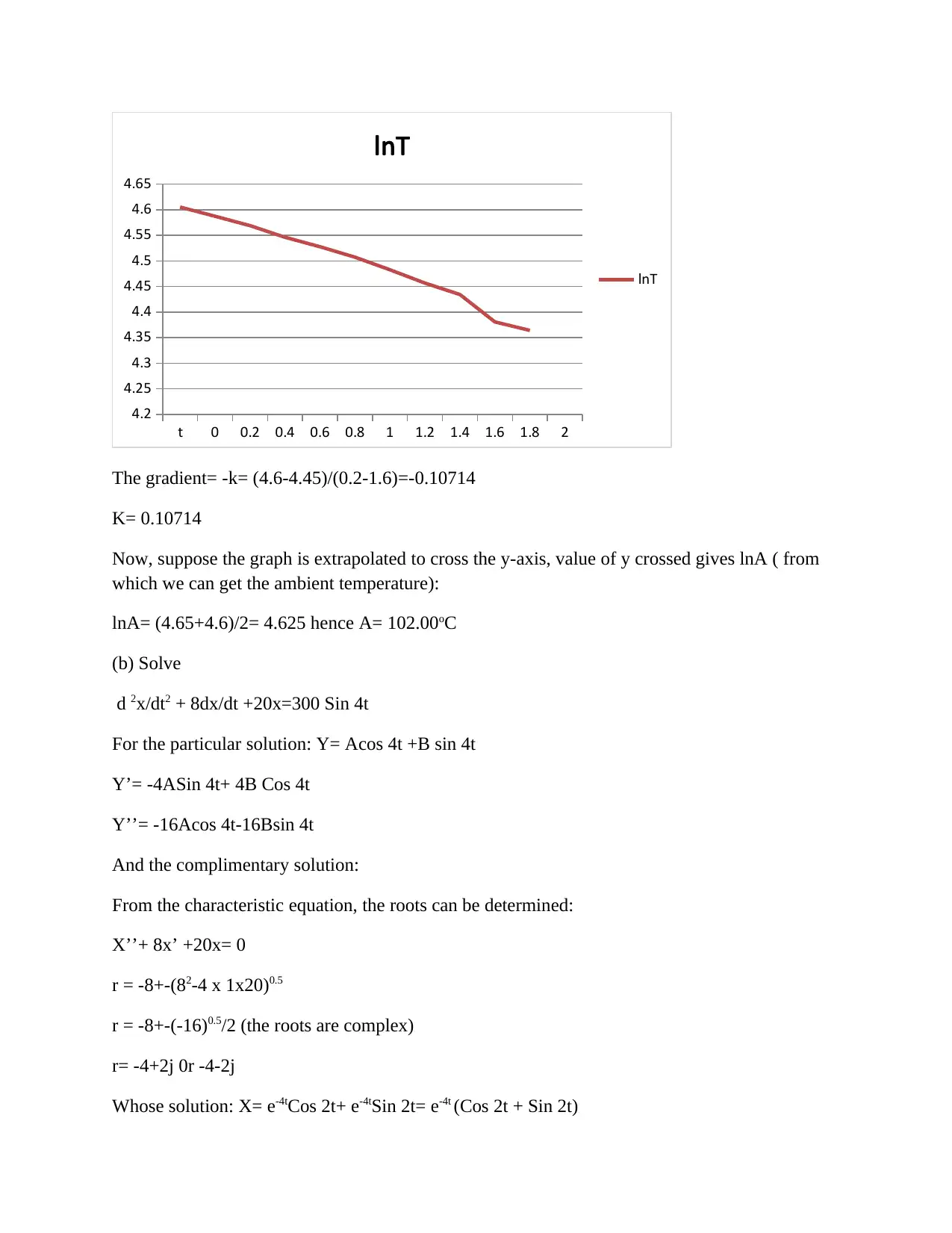
Solving Transcendental Functions using Euler's Method

The provided assignment consists of seven tasks that involve solving transcendental functions using Euler's method. The tasks include finding the general solution for a damped wave equation, determining the particular solution when initial conditions are given, and improving Euler's method by making intervals infinitesimally close. Additionally, an experiment is discussed to improve recording accuracy in temperature measurements. A reference section provides links to relevant online resources.

SOLUTIONS TO THE QUESTIONS
Task 1) Check excel file
Substituting in the given d.e
dT/dt= -k(90-18)
dT/dt= -72K
The first T1= T0+dT/dt= To-72k
Hence about 10 iterations are performed with h being 0.1
0
0.2
0.4
0.600000000000001
0.8
1
1.2
1.4
1.6
1.8
2
0
50
100
150
200
250
300
350
400
T
T
Figure 1: When K= 1
Task 2) Method of separation
Given dT/dt= -k(T-A)…(i)
This has to be first written in this form: A(x)dx + B(y) dy= 0 and then it can be integrated all
over.
Let dt represented by dy and dt represented by dx. From equation (i) I undertake the following
gymnastics:
dT/dt= -kT+kA
or dT/dt+kT-kA= 0

implying : dT= -k(T-A) dt
in terms of y and x:
dy= -k(y-A)dx
dy/k= -k/k(y-A)dx , (y-A)dx +1/kdy=0
or kdx= -dy/(y-A)
integrating both sides: ∫kdx= -∫dy/(y-A)
kx= -ln(y-A)
mathematically equivalent to: e-kx= y-A
hence T= e-kt +A, (Assume ambient temperature of 250C)
t
0.02
0.05
0.08
0.11
0.14
0.17
0.2
0.5
0.8
1.1
1.4
1.7
2
297.6
297.8
298
298.2
298.4
298.6
298.8
299
299.2
T
T
Figure 1: Temperature graph given K= 1.0

0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0.4
0.6
0.8 1
1.2
1.4
1.6
1.8 2
298
298.2
298.4
298.6
298.8
299
299.2
T
T
Figure 2: Temperature graph given K= 0.5
0
0.03
0.06
0.09
0.12
0.15
0.18
0.3
0.6
0.9
1.2
1.5
1.8
298.7
298.75
298.8
298.85
298.9
298.95
299
299.05
T
T
Figure 3: Temperature graph given K= 0.1
As K value is reduced from k= 1.0 to 0.5, the graph loses the nonlinearity and becomes almost a
straight line. Rate of cooling can be said to be uniform in figure 3 and non-uniform in figure 1
and partly in 2. This is because there is drastic change in slope for the first graph and in graph 3,
the change is linear.
Task 3: (a) check the graph on the excel file attached

t 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
4.2
4.25
4.3
4.35
4.4
4.45
4.5
4.55
4.6
4.65
lnT
lnT
The gradient= -k= (4.6-4.45)/(0.2-1.6)=-0.10714
K= 0.10714
Now, suppose the graph is extrapolated to cross the y-axis, value of y crossed gives lnA ( from
which we can get the ambient temperature):
lnA= (4.65+4.6)/2= 4.625 hence A= 102.00oC
(b) Solve
d 2x/dt2 + 8dx/dt +20x=300 Sin 4t
For the particular solution: Y= Acos 4t +B sin 4t
Y’= -4ASin 4t+ 4B Cos 4t
Y’’= -16Acos 4t-16Bsin 4t
And the complimentary solution:
From the characteristic equation, the roots can be determined:
X’’+ 8x’ +20x= 0
r = -8+-(82-4 x 1x20)0.5
r = -8+-(-16)0.5/2 (the roots are complex)
r= -4+2j 0r -4-2j
Whose solution: X= e-4tCos 2t+ e-4tSin 2t= e-4t (Cos 2t + Sin 2t)

Back to the particular solution, putting them back in the given de:
-16Acos 4t-16Bsin 4t +8(-4ASin 4t+ 4B Cos 4t) +20(Acos 4t +B sin 4t) =
(-32A- 16B +20 B) Sin 4t + (32 B-16A +20 A) Cos 4t
(-32A-4B) Sin 4t +(32B + 4B) Cos 4t + e-4tCos 2t + e-4t Sin 2t
Which on further simplification, we obtain:
X= e-4t (A Cos 2t + B sin 2t) +15/13(sin 4t -8 Cos 4t)
Task 4) let the characteristic equation be:
X’’+ 7x’ +12 x = 0
Whose roots are:
r = -7 +-(72- 4 x1 x12)0.5/2
r= -3.5 0r 3.5
hence the general solution is : X= C1e3.5t+ C2e-3.5t
For particular solution, the boundary conditions: t=0, x= 3 and x’= -7
C1= 3, X= 3e3.5t
X’= 12.25e3.5t + 3.5 C2e-3.5t
Substituting: -7=12.25 + 3.5 C2
C2= -19.25/3.5= -5.5
Hence the particular solution: X= 3.5e3.5t-5.5 e-3.5t
(b) 9x’’-12x’ + 4x= 3t-1
General solution
From the characteristic equation: 9x’’-12x’+4x= 0
The roots are: r= 12+-(122-4x9x4)/2x9
r = 12/18=2/3 (roots are repetitive)
hence general solution: X= C1e2/3t + C2te2/3t

For the complimentary solution:
f(t) = 3t-1
the accompanying Xp= Ct+ D
X’ = C
X= 0
Subtituting in the de:
-12(C) +4(Ct+D)=3t-1
Comparing the coefficients:
4C= 3, C= ¾
-12C +4D=-1
-9+ 4D=-1
4D= 8
D= 2
Hence X= Xc+Xp= Ce2/3t + Cte2/3t+ 3/4t+ 2
Task 5: Particular solution when
t = 0, x= 0, dx/dt=-4/3
Note: putting the conditions above in the equation: 0 = C+2, C= -2
Hence: X= -2e2/3t-2te2/3t+3/4t+2
Task 6: Euler’s method and how it could be improved
This is among the numerical methods used to solve transcendental functions; in other words
those functions with no defined method of determining their exact solutions
(Rosettacode.org. ,2018). It is based on iterations such that a number of solutions are undertaken
until solution obtained nears the exact one. Euler’s method can be improved by making the

intervals infinitesimally close. This can be implemented using developed computational software
such as mat lab or one can develop an app to implement the improved Euler Method. This should
actually be an improvement project if one possesses coding skills and is greatly interested in
making Engineering Mathematics a lot more interesting.
Task 7: Comment on experiment and how it could be improved further
The recording accuracy needs to be improved by providing a temperature sensor that accurately
measures real time temperature without any error entertained as it will combine time at which
this is taken such that say the device is set at 2mins interval, it will exactly record the
temperature after every 2 minutes without delay. For this case, error could have arisen due to
delay in recording temperature at close intervals.
References
Bing.com. (2018). Differential Equations - Separable Equations. [online] Available at:
http://www.bing.com/cr?
IG=0A79AF121C53421697E009AFA17D2E9B&CID=1B6B7CC9DAFD64DF01D97762DB52
65C7&rd=1&h=G9zuZQfSQ0LwPup0Lce7sGSrnhsoVyQEbGL0rBvOol4&v=1&r=http%3a%2f
%2ftutorial.math.lamar.edu%2fclasses%2fde%2fseparable.aspx&p=DevEx,5086.1 [Accessed 7
Mar. 2018]
Mathworld.wolfram.com. (2018). Homogeneous Ordinary Differential Equation -- from
Wolfram MathWorld. [online] Available at:
http://mathworld.wolfram.com/HomogeneousOrdinaryDifferentialEquation.html [Accessed 7
Mar. 2018].
Rosettacode.org. (2018). Euler method - Rosetta Code. [online] Available at:
https://rosettacode.org/wiki/Euler_method [Accessed 7 Mar. 2018].
Takeda, H. (2015). Higher-order expansion of solutions for a damped wave equation. Asymptotic
Analysis, 94(1-2), pp.1-31.
Vlab.amrita.edu. (2018). Newton's Law of Cooling (Theory) : Heat & Thermodynamics Virtual
Lab : Physical Sciences : Amrita Vishwa Vidyapeetham Virtual Lab. [online] Available at:
http://vlab.amrita.edu/?sub=1&brch=194&sim=354&cnt=1 [Accessed 7 Mar. 2018].
YouTube. (2018). Second-Order Non-Homogeneous Differential (KristaKingMath). [online]
Available at: https://www.youtube.com/watch?v=h3SCtTtlCKU [Accessed 7 Mar. 2018].