General Physics I Assignment: Mechanics and Motion Problem Set
VerifiedAdded on 2023/06/03
|8
|1855
|151
Homework Assignment
AI Summary
This General Physics I assignment from Fall 2018 focuses on mechanics and motion problems. It includes questions on projectile motion involving a tennis ball, analyzing its maximum height, flight time, and range. Another problem examines the motion of a car along a highway, requiring the creation of acceleration and velocity graphs, as well as the calculation of average velocity. The assignment further explores force and motion through a truck acceleration problem, including calculations of required force and skidding distance. Gravitational forces between masses are also investigated, along with a problem on dropping supplies from a rescue plane. Finally, the assignment concludes with a problem analyzing the forces acting on a block on an inclined plane, determining the maximum frictional force and the angle at which the block begins to slide. Desklib offers a wide range of solved assignments and study resources for students.

GENERAL PHYSICS I Fall, 2018
ASSIGNMENT I DATE DUE: 2/10/2018
Show all working: An answer without narrative and methodical calculations is without merit. Provide a
sketch, where appropriate or as directed. Give at least one detailed reference for each question.
1. A tennis ball is struck by a tennis racket in such a manner that the ball can be viewed as a
projectile. If the ball was struck at an angle of 35° above the horizontal with a velocity of 50 m/s
by a player who is 2 m tall, find:
a. The maximum height that the ball will reach above the tennis court.
Figure 1: Path followed by the ball
The maximum height reached by the ball is given by:
H= v0
2 sin2 ( α )
2 g
Where v0 is the initial velocity [m/s], αstruck at an angle [degrees] and g is the earth’s
gravitational acceleration (g=9.80665 )[N/kg]. Therefore,
H=
v0
2 sin2 ( α ) [ m
s ]
2
2 g [ m
s2 ] =
502 sin2 ( 35 ) [ m
s ]
2
2× 9.80665 [ m
s2 ] ¿ 43.9345 m
The maximum height reached by the ball is 43.9345 meters
b. The time it will take for the ball to reach its maximum height.
He flight time, t: The time taken for the ball to hit the ground for the first time is given
by:
ASSIGNMENT I DATE DUE: 2/10/2018
Show all working: An answer without narrative and methodical calculations is without merit. Provide a
sketch, where appropriate or as directed. Give at least one detailed reference for each question.
1. A tennis ball is struck by a tennis racket in such a manner that the ball can be viewed as a
projectile. If the ball was struck at an angle of 35° above the horizontal with a velocity of 50 m/s
by a player who is 2 m tall, find:
a. The maximum height that the ball will reach above the tennis court.
Figure 1: Path followed by the ball
The maximum height reached by the ball is given by:
H= v0
2 sin2 ( α )
2 g
Where v0 is the initial velocity [m/s], αstruck at an angle [degrees] and g is the earth’s
gravitational acceleration (g=9.80665 )[N/kg]. Therefore,
H=
v0
2 sin2 ( α ) [ m
s ]
2
2 g [ m
s2 ] =
502 sin2 ( 35 ) [ m
s ]
2
2× 9.80665 [ m
s2 ] ¿ 43.9345 m
The maximum height reached by the ball is 43.9345 meters
b. The time it will take for the ball to reach its maximum height.
He flight time, t: The time taken for the ball to hit the ground for the first time is given
by:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

GENERAL PHYSICS I Fall, 2018
ASSIGNMENT I DATE DUE: 2/10/2018
t=
2 v0 sin ( α ) [ m
s ]
g [ m
s2 ]
Thus, the time it will take to reach to a maximum height is t
2, so
t
2 =2 v0 sin ( α )
g × 1
2 =t= v0 sin ( α )
g ¿
50 si n (35 ) [ m
s ]
9.80665 [ m
s2 ] =3.9244 s
Thus, the time taken the ball to reach maximum height is 2.9244 second
c. How far away will the ball be from the player when it hits the ground on the other side
of the net?
The horizontal distance i.e. Range, R is given by;
R= v0
2 sin ( 2 α )
g
Thus:
R= v0
2 sin ( 2 α )
g =
502 ×sin ( 2 ×35 ) [ m
s ] 2
9.80665 [ m
s2 ] ¿ 239.5550 m
The distance the ball hits the ground is 239.5550 meters away
d. Will a second player standing 15m away from the first be able to return this ball if she
can reach a height of 4 m above the ground with her racket?
The range at given time, t is
R=v0 t sin ( α )− 1
2 g t2
15=50t .sin ( 35 ) [ m
s ]−
9.80665 t2
[ m
s2 ]
2
4.903325 t2−28.6788282 t+15=0
ASSIGNMENT I DATE DUE: 2/10/2018
t=
2 v0 sin ( α ) [ m
s ]
g [ m
s2 ]
Thus, the time it will take to reach to a maximum height is t
2, so
t
2 =2 v0 sin ( α )
g × 1
2 =t= v0 sin ( α )
g ¿
50 si n (35 ) [ m
s ]
9.80665 [ m
s2 ] =3.9244 s
Thus, the time taken the ball to reach maximum height is 2.9244 second
c. How far away will the ball be from the player when it hits the ground on the other side
of the net?
The horizontal distance i.e. Range, R is given by;
R= v0
2 sin ( 2 α )
g
Thus:
R= v0
2 sin ( 2 α )
g =
502 ×sin ( 2 ×35 ) [ m
s ] 2
9.80665 [ m
s2 ] ¿ 239.5550 m
The distance the ball hits the ground is 239.5550 meters away
d. Will a second player standing 15m away from the first be able to return this ball if she
can reach a height of 4 m above the ground with her racket?
The range at given time, t is
R=v0 t sin ( α )− 1
2 g t2
15=50t .sin ( 35 ) [ m
s ]−
9.80665 t2
[ m
s2 ]
2
4.903325 t2−28.6788282 t+15=0

GENERAL PHYSICS I Fall, 2018
ASSIGNMENT I DATE DUE: 2/10/2018
When the horizontal distance is 15, the time t is:
t= ( 28.6788282 ± √ 28.67882822− ( 4 ×15 × 4.903325 ) )
2 ( 4.903325 ) s¿ 0.5806856685 seconds
The height at t=0.5806856685 seconds is:
h=V 0 t . cos ( α )¿ 50 [ m
s ] ×0.5806856685 [ s ] × cos ( 35 ) ¿ 23.7835 m
The second player standing 15m away, will not be able to return the ball since the ball
is 23.7835 meter above the ground, and the maximum height he can reach is 4 meters
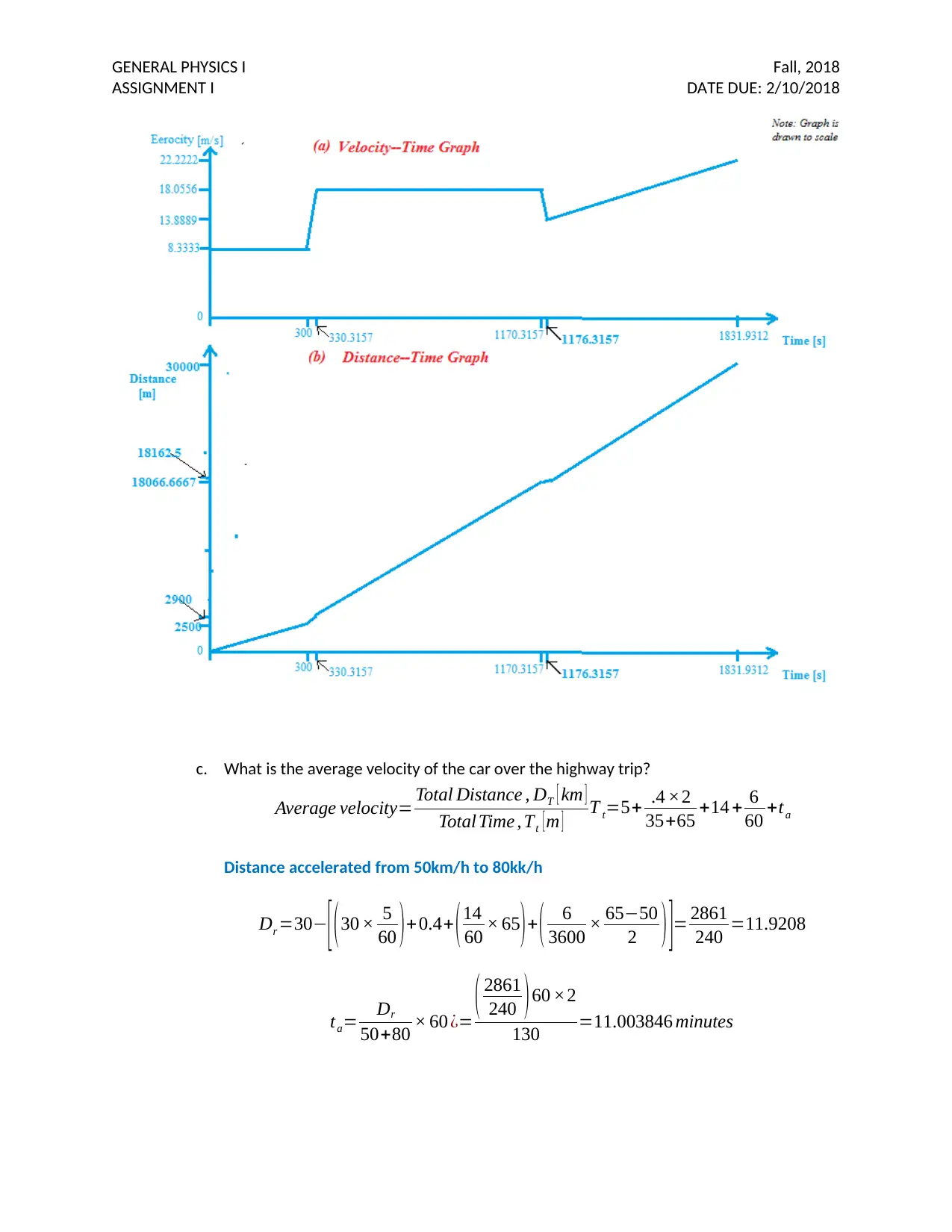
2. A car is travelling along a relatively straight highway 30 km long. For the first 5 minutes of the
journey, the car travels at a constant velocity of 30 km/h. After this, the car accelerates to 65
km/h within a 400 m stretch, and stays at this velocity for 14 minutes. The car slows to 50 km/h
very quickly (in about 6 seconds) in order to avoid running into a car in front, and slowly sped up
to 80 km/h over the remainder of the length of the highway (i.e. reached 80 km/h at the end of
the highway)
a. Draw a graph showing the acceleration of the car on the highway (v vs. t graph)
b. Draw a graph showing the velocity of the car on the highway (x vs t graph)
ASSIGNMENT I DATE DUE: 2/10/2018
When the horizontal distance is 15, the time t is:
t= ( 28.6788282 ± √ 28.67882822− ( 4 ×15 × 4.903325 ) )
2 ( 4.903325 ) s¿ 0.5806856685 seconds
The height at t=0.5806856685 seconds is:
h=V 0 t . cos ( α )¿ 50 [ m
s ] ×0.5806856685 [ s ] × cos ( 35 ) ¿ 23.7835 m
The second player standing 15m away, will not be able to return the ball since the ball
is 23.7835 meter above the ground, and the maximum height he can reach is 4 meters
2. A car is travelling along a relatively straight highway 30 km long. For the first 5 minutes of the
journey, the car travels at a constant velocity of 30 km/h. After this, the car accelerates to 65
km/h within a 400 m stretch, and stays at this velocity for 14 minutes. The car slows to 50 km/h
very quickly (in about 6 seconds) in order to avoid running into a car in front, and slowly sped up
to 80 km/h over the remainder of the length of the highway (i.e. reached 80 km/h at the end of
the highway)
a. Draw a graph showing the acceleration of the car on the highway (v vs. t graph)
b. Draw a graph showing the velocity of the car on the highway (x vs t graph)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
GENERAL PHYSICS I Fall, 2018
ASSIGNMENT I DATE DUE: 2/10/2018
c. What is the average velocity of the car over the highway trip?
Average velocity= Total Distance , DT [ km ]
Total Time , Tt [ m ] T t=5+ .4 ×2
35+65 +14 + 6
60 +ta
Distance accelerated from 50km/h to 80kk/h
Dr =30− [ ( 30 × 5
60 ) +0.4+ ( 14
60 × 65 ) + ( 6
3600 × 65−50
2 ) ]= 2861
240 =11.9208
ta= Dr
50+80 × 60 ¿= ( 2861
240 )60 ×2
130 =11.003846 minutes
ASSIGNMENT I DATE DUE: 2/10/2018
c. What is the average velocity of the car over the highway trip?
Average velocity= Total Distance , DT [ km ]
Total Time , Tt [ m ] T t=5+ .4 ×2
35+65 +14 + 6
60 +ta
Distance accelerated from 50km/h to 80kk/h
Dr =30− [ ( 30 × 5
60 ) +0.4+ ( 14
60 × 65 ) + ( 6
3600 × 65−50
2 ) ]= 2861
240 =11.9208
ta= Dr
50+80 × 60 ¿= ( 2861
240 )60 ×2
130 =11.003846 minutes
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

GENERAL PHYSICS I Fall, 2018
ASSIGNMENT I DATE DUE: 2/10/2018
T t= 745
38 +11.003=30.609109 minuts=0.5101518219 hours
vaverage= DT [ km ]
Tt [ hours ] = 30 [ km ]
0.51015 [ h ] =58.8060 km/h
The average speed is 58.8060 km/h
3. A truck of mass 4000 kg is travelling along the road. If the truck is travelling at a velocity of 60
km/h and accelerates to 85 km/h in 14 seconds.
a. How much force would the tires need to exert on the road in order for the truck to
change its speed?
From newton’s law of motion:
F=ma
Where F is the force,
m is the mass and
a is the acceleration
a= ∆ v
t =
( 85 km × 1000 m
1 km
1 h× 3600 s
1 h )−
( 60 km× 1000 m
1km
1 h × 3600 s
1 h )14 [ s ] =0.496031746 m/ s2
∴ F=4000 kg × 0.496031746 m
s =1984.126984 kg m
s2 ¿ 1984.1270 N
b. If the truck slams on the brakes travelling at 85 km/h, causing the wheels to stop rolling
and instead skid, how far will the truck skid before coming to a stop (μs = 0.7 between
tires and road surface) Hint: truck is decelerating in a constant manner.
Speed in m/s is:
v=
85 km× 1000 m
1km
1 h × 3600 s
1 h
=23.611111 m/s
The skidding distance is:
From the conservation of energy law,
ASSIGNMENT I DATE DUE: 2/10/2018
T t= 745
38 +11.003=30.609109 minuts=0.5101518219 hours
vaverage= DT [ km ]
Tt [ hours ] = 30 [ km ]
0.51015 [ h ] =58.8060 km/h
The average speed is 58.8060 km/h
3. A truck of mass 4000 kg is travelling along the road. If the truck is travelling at a velocity of 60
km/h and accelerates to 85 km/h in 14 seconds.
a. How much force would the tires need to exert on the road in order for the truck to
change its speed?
From newton’s law of motion:
F=ma
Where F is the force,
m is the mass and
a is the acceleration
a= ∆ v
t =
( 85 km × 1000 m
1 km
1 h× 3600 s
1 h )−
( 60 km× 1000 m
1km
1 h × 3600 s
1 h )14 [ s ] =0.496031746 m/ s2
∴ F=4000 kg × 0.496031746 m
s =1984.126984 kg m
s2 ¿ 1984.1270 N
b. If the truck slams on the brakes travelling at 85 km/h, causing the wheels to stop rolling
and instead skid, how far will the truck skid before coming to a stop (μs = 0.7 between
tires and road surface) Hint: truck is decelerating in a constant manner.
Speed in m/s is:
v=
85 km× 1000 m
1km
1 h × 3600 s
1 h
=23.611111 m/s
The skidding distance is:
From the conservation of energy law,

GENERAL PHYSICS I Fall, 2018
ASSIGNMENT I DATE DUE: 2/10/2018
WE=KE=Fd=kmg dskid =1
2 m v2
dskid = v2
2 μsg
¿
23.611111 m
s
2× 0.7 ×9.80665 m
s2
=1.719759486 m ¿ 1.92 m
4. Two masses, 2 kg and 4 kg are separated by a distance of 2.5 m.
a. What is the gravitational force of each mass on the other?
Using Newton's Gravitation Equation
FG= G M 1 M2
D2
Where:
FG is the gravitational force
Gis the universal gravitation constant=6.673 x 10−11
M 1∧M 2is the two masses
D is the distance between the masses
Thus,
FG= G M 1 M2
D2 =
6.673 x 10−11 N m2
k g2 ×2 kg × 4 kg
2.52 m2
¿ 8.54144 × 10−11 N
b. If a third mass of 3.2 kg is placed directly between the two initial masses, at what
distance from the smaller mass will the gravitational force on the third mass from the
two masses be equal?
Let the distance from 2 kg mass to 3.2 kg mass bed, so the distance from 3.2 kg mass
to 4 kg mass is 2.5−d
G M 1 M 3
d2 = G M 3 M 2
( 2.5−d ) 2
( 2.5−d ) 2
d2 = G M 2 M3
G M 1 M3
= M 2
M 1
( 2.5−d ) 2
d2 = 4
2 =2
2 d2=6.25−5 d+ d2d2 +5 d−6.25=0Finding d using quadratic equation is:
ASSIGNMENT I DATE DUE: 2/10/2018
WE=KE=Fd=kmg dskid =1
2 m v2
dskid = v2
2 μsg
¿
23.611111 m
s
2× 0.7 ×9.80665 m
s2
=1.719759486 m ¿ 1.92 m
4. Two masses, 2 kg and 4 kg are separated by a distance of 2.5 m.
a. What is the gravitational force of each mass on the other?
Using Newton's Gravitation Equation
FG= G M 1 M2
D2
Where:
FG is the gravitational force
Gis the universal gravitation constant=6.673 x 10−11
M 1∧M 2is the two masses
D is the distance between the masses
Thus,
FG= G M 1 M2
D2 =
6.673 x 10−11 N m2
k g2 ×2 kg × 4 kg
2.52 m2
¿ 8.54144 × 10−11 N
b. If a third mass of 3.2 kg is placed directly between the two initial masses, at what
distance from the smaller mass will the gravitational force on the third mass from the
two masses be equal?
Let the distance from 2 kg mass to 3.2 kg mass bed, so the distance from 3.2 kg mass
to 4 kg mass is 2.5−d
G M 1 M 3
d2 = G M 3 M 2
( 2.5−d ) 2
( 2.5−d ) 2
d2 = G M 2 M3
G M 1 M3
= M 2
M 1
( 2.5−d ) 2
d2 = 4
2 =2
2 d2=6.25−5 d+ d2d2 +5 d−6.25=0Finding d using quadratic equation is:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

GENERAL PHYSICS I Fall, 2018
ASSIGNMENT I DATE DUE: 2/10/2018
d= (−5± √25− ( 4 ×6.25 ) )
2 =1.035533906∨−6.035533906
Distance cannot be negative, so the distance is 1.035533906 meters, from smaller
mass that will make the gravitational force on the third mass equal into the two
masses from be equal
5. A rescue plane wants to drop supplies to isolated mountain climbers on a rocky ridge 235 m
below. If the plane is travelling horizontally with a speed of 250 km/h how far in advance of the
recipients (horizontal distance) must the goods be dropped?
The time required to fall 235 m at V 0 x=0h= g t2
2
∴ t= √ 2 h
g =
√ 2 ×235 m
9.80665 m
s2
=6.9229 seconds
Speed of the plane V 0 y=250 km
h =
250 km× 1000 m
1 km
1 h × 3600 s
1 h
=69.444444 m/ s¿ 69.4444 m
s
In 6.9229 seconds, the plane will travel:
d0 x=69.44444 m
s ×6.9229 s=480.7575343m
So the package has to be dropped 480.7575343meters before the target
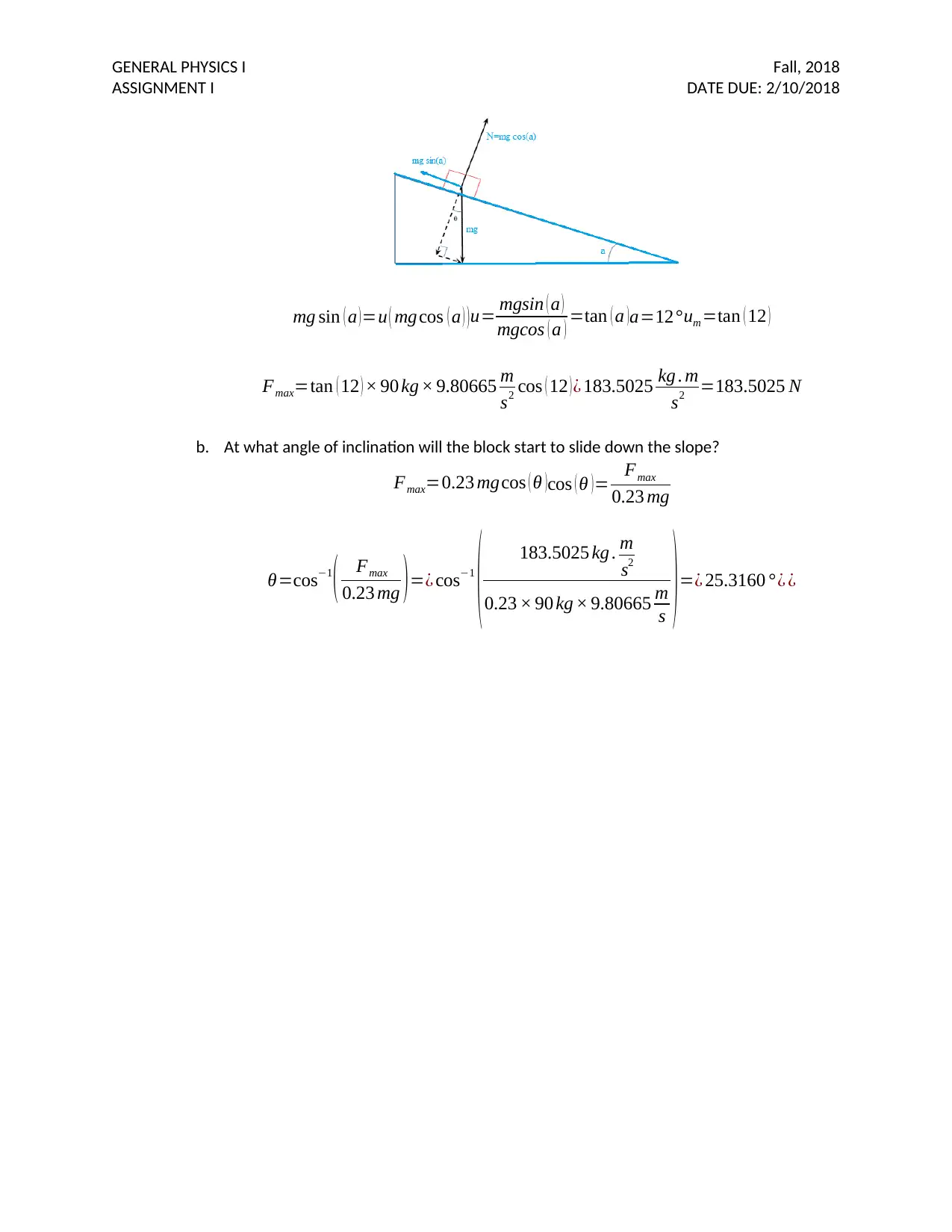
6. A block of mass 90 kg sits on a slope with an angle of inclination 12° above the horizontal. The
coefficients of friction between the block and the slope are μk = 0.03 and μs = 0.2.
a. What is the maximum frictional force that will allow the block to stay in place?
The free body diagram is given below
ASSIGNMENT I DATE DUE: 2/10/2018
d= (−5± √25− ( 4 ×6.25 ) )
2 =1.035533906∨−6.035533906
Distance cannot be negative, so the distance is 1.035533906 meters, from smaller
mass that will make the gravitational force on the third mass equal into the two
masses from be equal
5. A rescue plane wants to drop supplies to isolated mountain climbers on a rocky ridge 235 m
below. If the plane is travelling horizontally with a speed of 250 km/h how far in advance of the
recipients (horizontal distance) must the goods be dropped?
The time required to fall 235 m at V 0 x=0h= g t2
2
∴ t= √ 2 h
g =
√ 2 ×235 m
9.80665 m
s2
=6.9229 seconds
Speed of the plane V 0 y=250 km
h =
250 km× 1000 m
1 km
1 h × 3600 s
1 h
=69.444444 m/ s¿ 69.4444 m
s
In 6.9229 seconds, the plane will travel:
d0 x=69.44444 m
s ×6.9229 s=480.7575343m
So the package has to be dropped 480.7575343meters before the target
6. A block of mass 90 kg sits on a slope with an angle of inclination 12° above the horizontal. The
coefficients of friction between the block and the slope are μk = 0.03 and μs = 0.2.
a. What is the maximum frictional force that will allow the block to stay in place?
The free body diagram is given below
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
GENERAL PHYSICS I Fall, 2018
ASSIGNMENT I DATE DUE: 2/10/2018
mg sin ( a )=u ( mgcos ( a ) ) u= mgsin ( a )
mgcos ( a ) =tan ( a )a=12° um =tan ( 12 )
Fmax=tan ( 12 ) × 90 kg × 9.80665 m
s2 cos ( 12 )¿ 183.5025 kg . m
s2 =183.5025 N
b. At what angle of inclination will the block start to slide down the slope?
Fmax=0.23 mgcos ( θ )cos ( θ )= Fmax
0.23 mg
θ=cos−1
( Fmax
0.23 mg )=¿ cos−1
( 183.5025 kg . m
s2
0.23 × 90 kg × 9.80665 m
s )=¿ 25.3160 °¿ ¿
ASSIGNMENT I DATE DUE: 2/10/2018
mg sin ( a )=u ( mgcos ( a ) ) u= mgsin ( a )
mgcos ( a ) =tan ( a )a=12° um =tan ( 12 )
Fmax=tan ( 12 ) × 90 kg × 9.80665 m
s2 cos ( 12 )¿ 183.5025 kg . m
s2 =183.5025 N
b. At what angle of inclination will the block start to slide down the slope?
Fmax=0.23 mgcos ( θ )cos ( θ )= Fmax
0.23 mg
θ=cos−1
( Fmax
0.23 mg )=¿ cos−1
( 183.5025 kg . m
s2
0.23 × 90 kg × 9.80665 m
s )=¿ 25.3160 °¿ ¿
1 out of 8
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





