Kinematics, Kinetics, and Vibrations: Solved Problems

This article provides solutions to problems related to Kinematics, Kinetics, and Vibrations. It covers topics such as angular velocity, acceleration, equations of motion, damping ratio, undamped natural frequency, and damped natural frequency. The solutions are provided in a step-by-step manner with diagrams and equations. The problems are solved using the principles of physics and mechanics.

Part 1 – Kinematics
A series of small machine components being moved by a conveyor belt pass over a 120 mm
radius idler pulley, as shown in Figure 1. At the instant shown, the velocity of Point A is 300
mm/s to the left and it acceleration is 180 mm/s2 to the right. Determine
Task 1A: The angular velocity of the idler pulley
Task 1B: The angular acceleration of the idler pulley
Task 1C: The total acceleration of the machine component at B
Task 1D: The direction of the angular acceleration vector
Solution:
Task 1A: The angular velocity of the idler pulley
Radius of the idler pulley rB = 120 mm
Linear Velocity at A, V A =300 m/s=¿ Linear Velocity at B,V B (towards left)
Linear velocity V =radius× angular velocity=r × ω
ω= V
r
Therefore, angular velocity of the idler pulley at B, ω= V B
r B
= 300
120 =2.5 rad /s (anti-clockwise)
Task 1B: The angular acceleration of the idler pulley
Linear acceleration, aA = aB = 180 mm/s2 (towards right)

Linear acceleration a=angular acceration ×radius=αr
α= a
r
Therefore, angular acceleration of idler pulley in tangential direction at B,
α = aB
rB
=180
120 =1.5rad /s (clockwise direction)
Task 1C: The total acceleration of the machine component at B
Total acceleration aB= √ (a¿¿ B)t
2 +( a¿¿ B)n
2 ¿ ¿
(a ¿¿ B)n=rB ω2 = ( 120 ) ( 2.5 )2=750 mm/s2 ¿
Therefore, total acceleration aB= √1802 +7502=771 mm /s2
Task 1D: The direction of the angular acceleration vector
The direction of angular acceleration vector tanβ = (a¿¿ B)n
(a¿¿ B)t= 750
180 ¿
¿
β=Ta n−1
( 750
180 )=76.50
Part 2 – Kinetics
A. A sphere of radius r and mass m is projected along a rough horizontal surface with an initial
linear initial velocity v0 and initial angular velocity ω0 , as shown in Figure 2; the final velocity
of the sphere zero as it will stop moving.
Task 2AA: Draw the Free Body Diagram and Resultant Force Diagram for the sphere.
Task 2AB: Write the equations of motion for the sphere.

G
W
N
= G
r
Solution:
Task 2AA: Draw the Free Body Diagram and Resultant Force Diagram for the sphere.
Step 1:
Free body diagram:
Fig. 1.1 Free-body-diagram
Task 2AB: Write the equations of motion for the sphere.
Step 2:
Solve the equilibrium equations with the following conventions:
Rotation: Clockwise +ve Forces: Towards right +ve Upward +ve
Anti-clockwise −ve Towards left −ve Downward −ve
1. Algebraic sum of horizontal forces ∑ F x=0
m a=−μk mg
a=−μk g
2. Algebraic sum of vertical forces ∑ F y=0
N−W =0
N−mg=0
N=mg
3. Algebraic sum of all the moments ∑ M G =0
Fr−I α=0

μk mg− ( 2
3 m r2
)α=0
α= 5 μk g
2 r
4. Kinematic relations for a rigid body with no sliding condition are given by
v=v0 +a t
Where a=−μk g
Therefore, v=v0 +(−μk g)t
Angular velocity ω=ω0 +αt
Where, α= 5 μk g
2 r
Therefore,ω=0+ ( 5 μk g
2r )t
Since v1 =r ω1,
v0+ ( −μk g ) t1=r ( 5 μk g
2 r ) t1
t1= 2 v0
7 μk g
Since ω1=( 5 μk g
2 r )t1,
ω1=5 v0
7 r
Therefore, v1 =r ( 5 v0
7 r )
v1 =5 v0
7
B. A 240-mm-radius cylinder of mass 8 kg rests on a 3-kg carriage. The system is at rest when a
force P of magnitude 10 N is applied as shown in Figure 3. The cylinder rolls without sliding on
the carriage; and the mass of the wheels of the carriage can be neglected.
Task 2BA: Draw the Impulse and Momenta Diagram for the cylinder.
Task 2BB: Write the equation of motion for the cylinder.

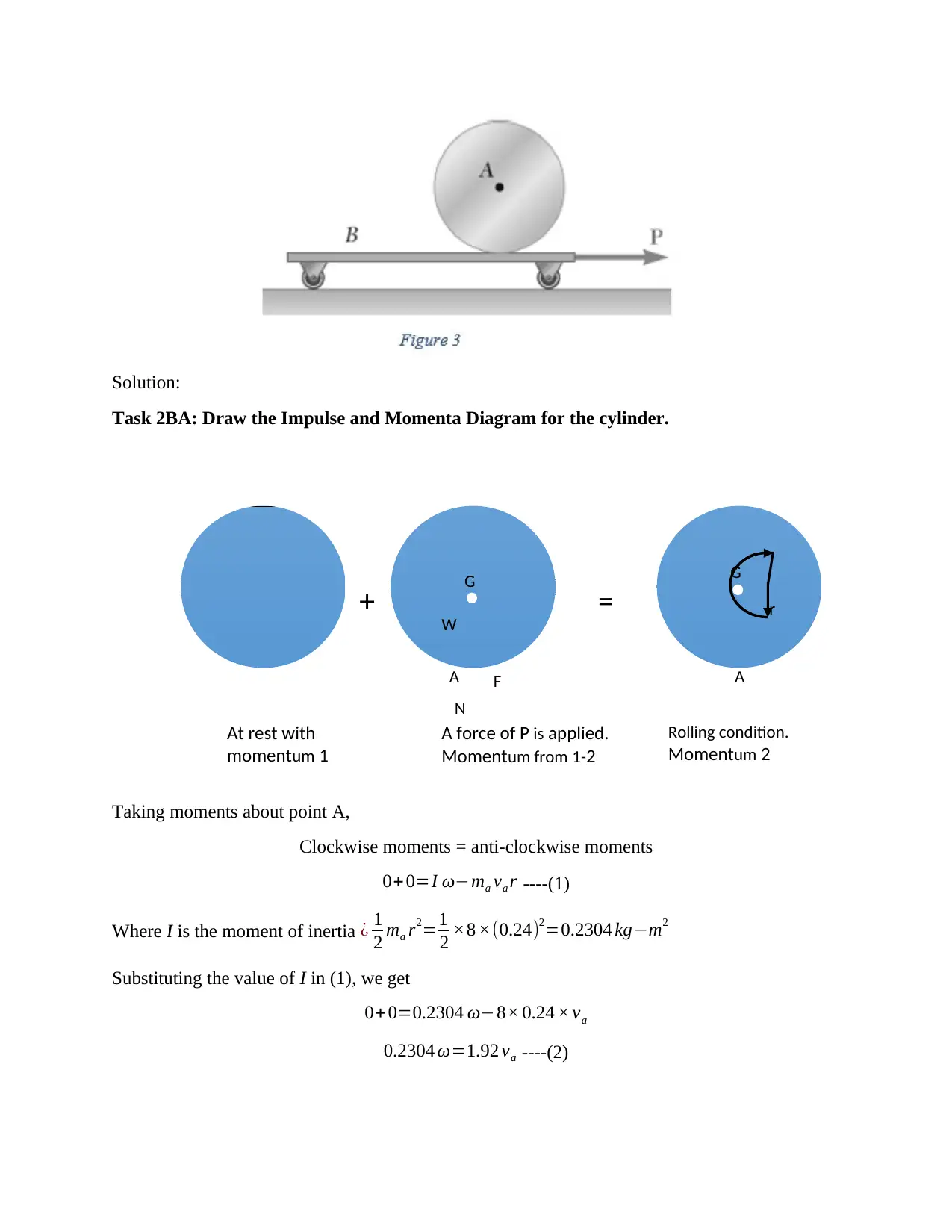
At rest with
momentum 1
A force of P is applied.
Momentum from 1-2
Rolling condition.
Momentum 2
G
W
FA
=
G
r+
A
N
Solution:
Task 2BA: Draw the Impulse and Momenta Diagram for the cylinder.
Taking moments about point A,
Clockwise moments = anti-clockwise moments
0+0=I ω−ma va r ----(1)
Where I is the moment of inertia ¿ 1
2 ma r2=1
2 ×8 ×(0.24)2=0.2304 kg−m2
Substituting the value of I in (1), we get
0+ 0=0.2304 ω−8× 0.24 × va
0.2304 ω=1.92 va ----(2)

A force of P is applied for
1.2 sec. Impulse from 1-2
G
W
=
G
r+
At rest with
momentum 1
Rolling condition.
Momentum 2
APt
Resolving the components along horizontal direction, we get
0+ Pt =ma va +mb vb
0+10 ×1.2=8 va +3 vb ----(3)
Task 2BB: Write the equation of motion for the cylinder.
For a rigid body rolling without slipping, velocity va=vb−rω
va=vb−0.24 ω ----(4)
To get the values of velocities, solve equations (2), (3), and (4).
Therefore, angular velocity ω=5.68 rad /s
Velocity of the cylinder va=0.706 m/s
Velocity of the carriage vb=2.12 m/s
Part 3 – Vibrations
In the system shown in Figure 4 a mass m is attached to a light rigid arm OA freely pivoted at O,
and makes small damped angular oscillations in the horizontal plane when displaced with a small
angular displacement θ and then released.
Task 3A: Show that the motion can be described by the following differential equation:
¨θ+ 4 c
9 m ˙θ+ 16 k
9 m θ=0

Given that the standard form is ˙θ+2 ζ ωn ˙θ+ ωn
2 θ=0 and taking the values for the parameters of
the system given in Figure 4, determine:
Task 3B: The undamped natural frequency 𝜔𝑛 in rad/s and hence its equivalent 𝑓𝑛 in Hz
Task 3C: The damping ratio ζ
Task 3D: The damped natural frequency 𝜔𝑑 in rad/s and hence its equivalent 𝑓𝑑 in Hz
Solution:
Task 3A:
The equation of motion of spring-mas-damper vibratory system is given by
m ¨x + c ˙x+ kx=0 ----(1)
Displacement of the spring x=lθ
From Figure 4, Inertia force ¿ m ¨x =m ( 3 l )2 ¨θ ----(2)
Damping force¿ c ˙x=c ( ( 2 l ) ˙θ) ----(3)
spring force ¿ kx =k ( 4 lθ ) ----(4)
About point O, using equations (1), (2), (3), and (4) we get
m ¿
m ¿ ----(5)

¨θ+ 4 c
9 m ˙θ+ 16 k
9 m θ=0
Task 3B: The undamped natural frequency 𝜔𝑛 in rad/s and hence its equivalent 𝑓𝑛 in Hz
Undamped natural frequency, ωn= √ k
m rad /s
ωn= √ 1.5 ×103
6 =15.81rad / s
Frequency, f n= ωn
2 π
f n= 15.81
2 π =2.52 Hz .
Task 3C: The damping ratio ζ
Damping ratio ζ = Damping coefficient c
critical dampingCc
Critical damping cc=2 √km=2 √1.5 × 103 × 6=94.87 N −sec/m
Damping ratio ζ = 200
94.87 =2.108
System is overdamped since the damping ratio is more than unity.
Task 3D: The damped natural frequency 𝜔𝑑 in rad/s and hence its equivalent 𝑓𝑑 in Hz
Damped natural frequency ωd=ωn √ ζ2−1
ωd=15.81 √ 2.1082−1
ωd=29.34 rad /s
f n= ωd
2 π = 29.34
2 π =4.67 Hz .