Mechanics and Kinematics Problems

This physics assignment focuses on solving problems related to mechanics and kinematics. It involves analyzing forces acting on objects, calculating velocities and accelerations in different directions, and applying concepts like equilibrium and Newton's laws of motion. The solutions are provided step-by-step with clear explanations for each calculation.

1 Theoretical question
a)
Spring constant
F= KE
Taking a single point from the line graph, say (20,56), where we have a force of 20N and
extension of 58 mm.
Converting the extension into meter = 56/1000 = 0.056 m
Spring constant (K) = force/extension
K= 20/0.056
K = 357.14 N/M
b)
Energy stores in the spring at any certain point of force application = PE = KE2
The application of 25N coincides with an extension of 70mm (0.07m)
Therefore energy at this point will be;
PE = ½*357.24*0.072
= 0.875 J
c)
Force required to extend the spring 300cm (3m)
F =KE
F= 357.14 * 3
= 1071.42 N
d) Assumptions made at c) above
 The spring extension limit is not achieved and that the spring extends uniformly
 The force and extension are one dimensional vector meaning they are acting in the same
direction
 The Hookes law is obeyed
2) Experiment task

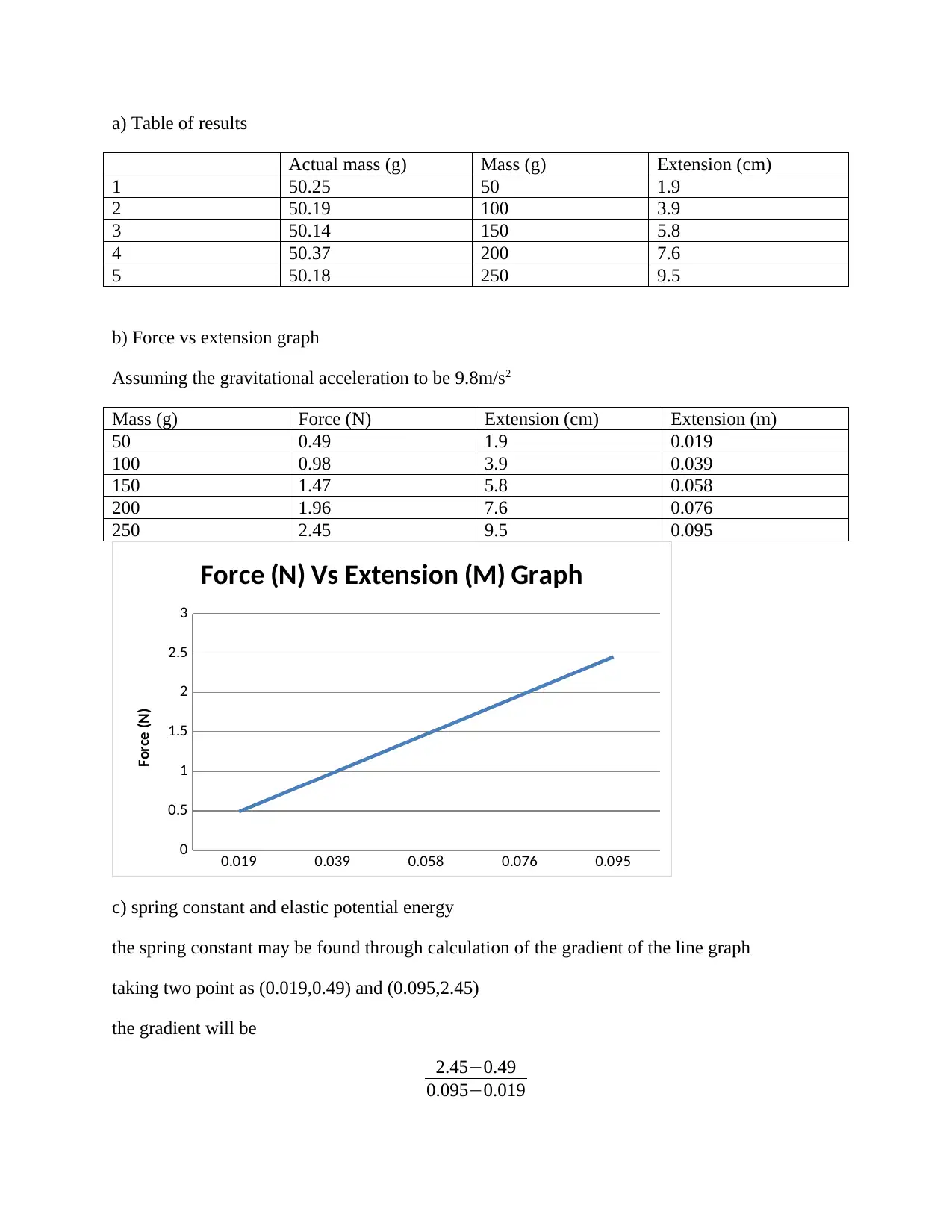
a) Table of results
Actual mass (g) Mass (g) Extension (cm)
1 50.25 50 1.9
2 50.19 100 3.9
3 50.14 150 5.8
4 50.37 200 7.6
5 50.18 250 9.5
b) Force vs extension graph
Assuming the gravitational acceleration to be 9.8m/s2
Mass (g) Force (N) Extension (cm) Extension (m)
50 0.49 1.9 0.019
100 0.98 3.9 0.039
150 1.47 5.8 0.058
200 1.96 7.6 0.076
250 2.45 9.5 0.095
0.019 0.039 0.058 0.076 0.095
0
0.5
1
1.5
2
2.5
3
Force (N) Vs Extension (M) Graph
Force (N)
c) spring constant and elastic potential energy
the spring constant may be found through calculation of the gradient of the line graph
taking two point as (0.019,0.49) and (0.095,2.45)
the gradient will be
2.45−0.49
0.095−0.019

= 1.96/0.076 = 25.79 N/m
PE = ½*K*extionsion2
PE = ½*25.79*0.0952
= 0.116375 J
d)
The spring is a Hookean. From the graph plotted, it is clear that the spring is able to obey the
Hookes law. The graph is a straight line showing that force is directly related to extension.
According to Hookes law, F =KE, where K is a constant known as the spring constant. This
spring is able to obey this rule and therefore can be regarded as a Hookean.
3) Theoretical question
a) Mass and weight of the beam
Assuming that the weight of the beam is x N/m
Taking the moments about the pivot to create the equilibrium situation
(1.5*0.15)+ (x *0.3*0.3/2) = (x*0.4*0.4/2) – (0.4*1.5)
0.225 + 0.045x = 0.08x – 0.6
Collecting like terms together
0.035x = 0.825
X = 23.57 N/m
The weight of the beam will be 23.57 N/m * 0.7 m = 16.5N
Assuming gravitational acceleration to be 10m/s2
Mass = 16.5/10 = 1.65 kg
b) Assumption on part a)
 the assumption is that the beam has weight which affects the equilibrium state
c) Reaction at pivot
The reaction at the pivot will be

Beam weight at section 1 + 1.5 N mass – Reaction at Pivot + Beams weight at section 2 – 1.5
force = 0
= (23.57 *0.3) + 1.5 – R + (23.57 * 0.4) – 1.5 = 0
= 7.07 + 1.5 – R + 9.43 – 1.5 = 0
R = 16.5 N
d) Distance of 150g when 1.5N is reduced to 1.1N
Taking moments about the pivot
(1.5*x) + (0.15*7.07) = (0.2*9.43) – (0.4*1.1)
1.5x + 1.0605= 1.886 - 0.44
= 1.5x = 1.886 – 0.44 -1.0605
= 1.5x = 0.3855
X = 0.257 m
The mass of 150g should move 25.7 cm from the pivot to maintain the equilibrium
4) Theoretical question
a)
Assuming that the weight of the beam is x N/m
Converting the mass into weight
(15+5)*10 = 200N
Taking the moments about the pivot to create the equilibrium situation
(200*1)+ (x *1.4*1.4/2) = (x*1.6*1.6/2) + (12*1.6*1.6/2)
200 + 0.98x = 1.28x – 15.36
Collecting like terms together
184.64 =0.3x
X = 615.47 N/m
The weight of the beam will be 615.47 N/m * 3 m = 1846.4N

Assuming gravitational pull to be 10kg
Mass = 1846.4/10 = 184.64 kg
b)
The reaction will all be equal to zero
The reaction of two masses + section 1beam self weight – reaction at pivot + UDL Load +
section 2 beam self weight = 0
= 200 + 615.47*0.7 – R + 615.47*0.8 + (12*1.6) =0
200+420.83- R + 492.37 +19.2 =
R = 1132.4 N
3)
a) Are forces vector or scalar?
Forces are vector quantities. From definition, force is a product of mass and acceleration. Mass is
a scalar quantity while acceleration is a vector quantity. The product of a vector and a scalar
quantity results to a vector quantity. Additionally, force has both magnitude and direction and
therefore making it a scalar quantity.
b)
658N
239N
700N
Solving the same using trigonometric functions of each force,
Force Horizontal component Vertical component
239 0 239
700 Cos(210) *700 = 606 to the
left
Sin(210) *700 = 350N down
ward
658 658 0
The sum of the horizontal and vertical forces nearly comes to zero. The small difference may be
due to the estimation error done on the initial values used.

c)
using trigonometry rules, and the following arrangement, we can find the extra force
380N
250N
XN
2502 + 3802 = X2
X = 454.86N
resultant force drawing
250N
33.30 380N
d)
F =MA
Vertical force = plane weight – Lcos(a) – D(sin(b)
= 325 x107 – 3.45x107cos(58) – 1.85x107sin(28)
= 325 x107 -18282214.62 - 8685223.91
= 3.22 x109N
A =F/M =3.22 x109/3.25 x108
Vertical acceleration = 9.93m/s
Horizontal acceleration
H= Dcos(b) – Lsin(a)
= 1.85x107 cos(28) –3.45x107 sin(58)

= 1.63 x107 – 2.93 x107
= -1.3 x107N
4)
a)
The standard unit of distance is meters and that of time is seconds. And since the speed and
velocity are changes in velocity per unit time, their SI unit results to m/s which is a combination
of the SI units of distances and time. The ST unit for acceleration will result from the SI unit of
velocity and that of time. Since acceleration is change in velocity per unit time, the SIunit will be
m/s divided by s resulting to m/s2.
b)
The SI units are important since they provide a key base of representing quantities uniformly.
These units are accepted in all parts and therefore offer uniformity when expressing quantities.
c)
88mph to m/s
= (88*1609)/ (60*60)
= 141592/ 3600
= 39.33 m/s
d)
Converting 85mph into m/s
= (85*1609)/3600
= 37.99 m/s
Resolving the northward and eastward velocities
37.99 m/s
180
Using trigonometry to resolve
The eastward velocity

Cos(18) *37.99 = 36.1 m/s to the right
The northward direction
sin(18) *37.99 = 11.74 m/s upward
e)
The southern velocity will be -11.74 m/s
f)
Northward velocity = 11.74 m/s
11.74m/s = 1174cm/s
1174*164/8.08 = 23827.8 Bobs/Mo