Engineering Science TMA: Analysis of Beams, Columns in Static Systems
VerifiedAdded on 2023/04/22
|13
|1584
|317
Homework Assignment
AI Summary
This document presents a detailed solution to an engineering assignment focused on static engineering systems. It includes calculations for vertical reactions at supports, shear force diagrams, bending moment calculations at 1m intervals, and bending moment diagrams for a loaded beam. The solution also covers the determination of maximum bending moment, maximum stress in a beam, and stress distribution through the beam's thickness. Furthermore, it addresses column buckling, including determining the minimum column length for buckling to occur, identifying the mode of failure, and calculating the expected failure load under different conditions. The document concludes with a bibliography, citing relevant resources on dynamics and control in mechanical engineering systems.

Engineering Systems 1
STATIC ENGINEERING SYSTEMS
A Research Paper on Engineering Systems By
Student’s Name
Name of the Professor
Institutional Affiliation
City/State
Year/Month/Day
STATIC ENGINEERING SYSTEMS
A Research Paper on Engineering Systems By
Student’s Name
Name of the Professor
Institutional Affiliation
City/State
Year/Month/Day
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Engineering Systems 2
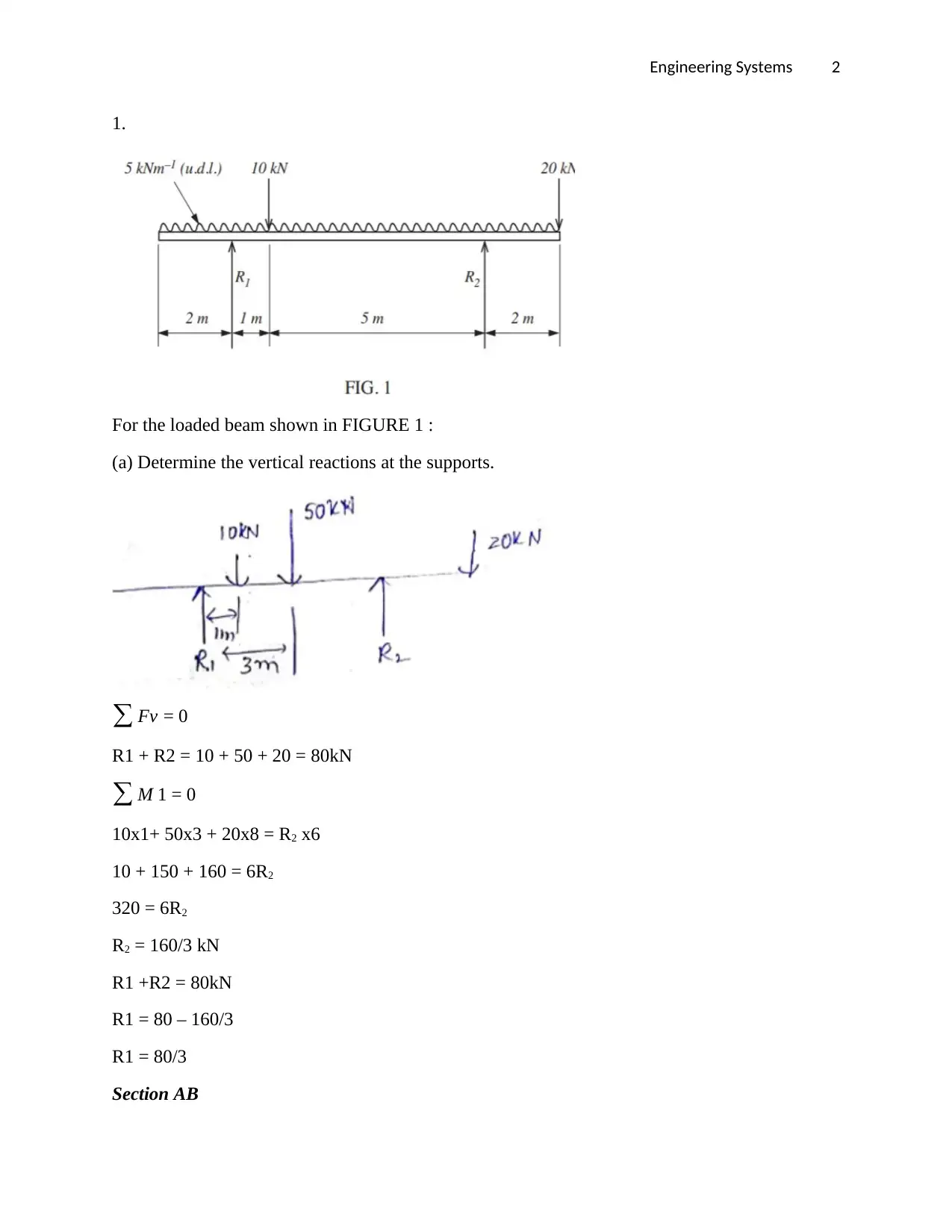
1.
For the loaded beam shown in FIGURE 1 :
(a) Determine the vertical reactions at the supports.
∑ Fv = 0
R1 + R2 = 10 + 50 + 20 = 80kN
∑ M 1 = 0
10x1+ 50x3 + 20x8 = R2 x6
10 + 150 + 160 = 6R2
320 = 6R2
R2 = 160/3 kN
R1 +R2 = 80kN
R1 = 80 – 160/3
R1 = 80/3
Section AB
1.
For the loaded beam shown in FIGURE 1 :
(a) Determine the vertical reactions at the supports.
∑ Fv = 0
R1 + R2 = 10 + 50 + 20 = 80kN
∑ M 1 = 0
10x1+ 50x3 + 20x8 = R2 x6
10 + 150 + 160 = 6R2
320 = 6R2
R2 = 160/3 kN
R1 +R2 = 80kN
R1 = 80 – 160/3
R1 = 80/3
Section AB

Engineering Systems 3
Fx = 20 + 5x; FA = 20
x = 2
FB = 20 + 5x2
FB = 30kN
Section AC
Fx = 20 – 160/3 + 5x; x = 2
FB = 20 – 160/3 + 10
= -70/3
(x = 7)
Fc = 20 – 100/3 + 5x7
= 55 – 160/3 = +85/3
Section CD
Fx = 20 – 160/3 + 10 + 5x
Fx = 20 + 5x; FA = 20
x = 2
FB = 20 + 5x2
FB = 30kN
Section AC
Fx = 20 – 160/3 + 5x; x = 2
FB = 20 – 160/3 + 10
= -70/3
(x = 7)
Fc = 20 – 100/3 + 5x7
= 55 – 160/3 = +85/3
Section CD
Fx = 20 – 160/3 + 10 + 5x
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Engineering Systems 4
(x = 7)
Fc = 20 – 160/3 + 10 + 35
= 65 – 160/3
= 35/3
(x = 8)
FD = 20 – 160/3 + 10 + 40
= 70 – 160/3
= 50/3 kN
Section DE
Fx = 20 – 160/3 + 10 -80/3 +5x
(x = 8)
FA = 20 – 80 + 10 + 40
= -10kN
(x = 10)
FA = 20 – 80 + 10 + 50
FA = 0
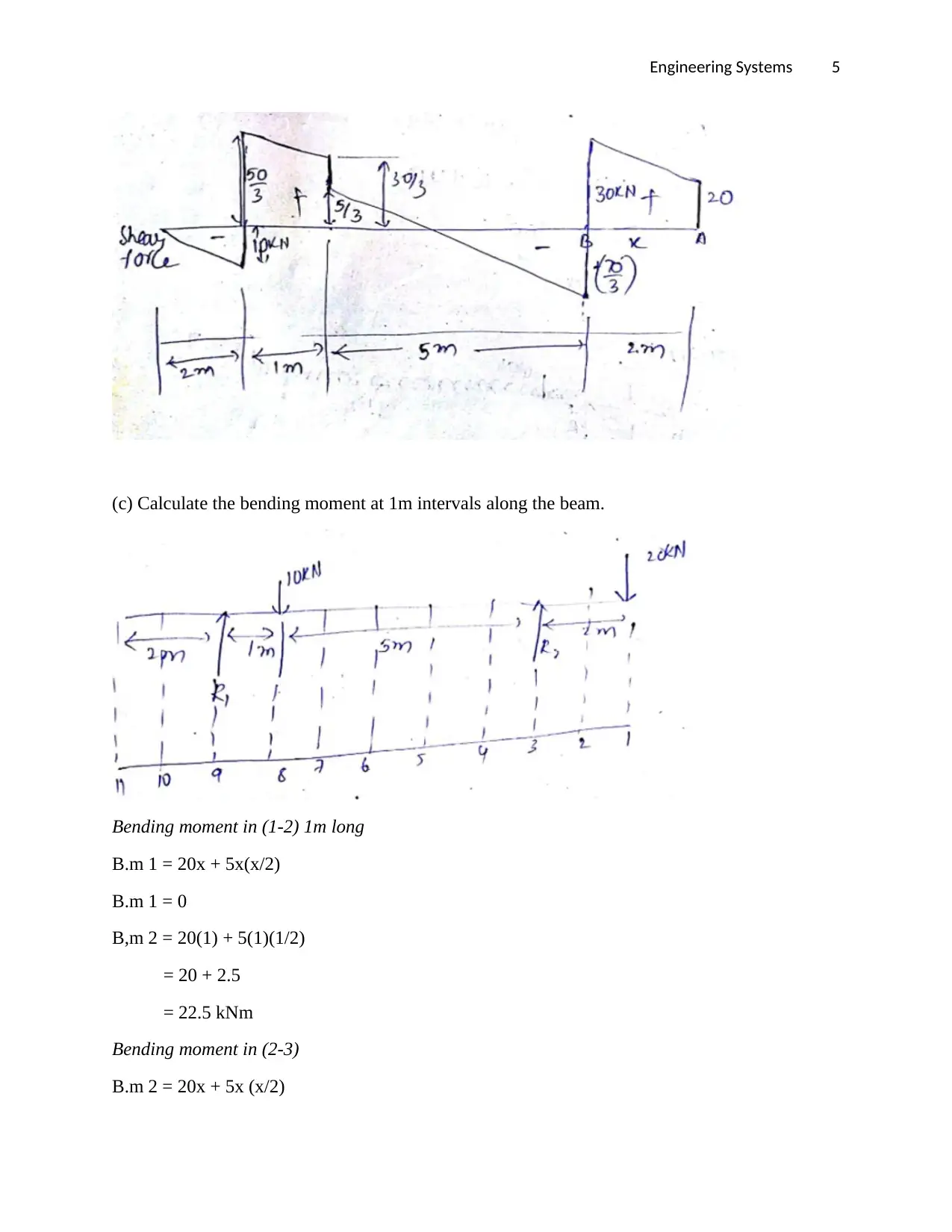
(b) Sketch the shear force diagram for the beam.
(x = 7)
Fc = 20 – 160/3 + 10 + 35
= 65 – 160/3
= 35/3
(x = 8)
FD = 20 – 160/3 + 10 + 40
= 70 – 160/3
= 50/3 kN
Section DE
Fx = 20 – 160/3 + 10 -80/3 +5x
(x = 8)
FA = 20 – 80 + 10 + 40
= -10kN
(x = 10)
FA = 20 – 80 + 10 + 50
FA = 0
(b) Sketch the shear force diagram for the beam.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Engineering Systems 5
(c) Calculate the bending moment at 1m intervals along the beam.
Bending moment in (1-2) 1m long
B.m 1 = 20x + 5x(x/2)
B.m 1 = 0
B,m 2 = 20(1) + 5(1)(1/2)
= 20 + 2.5
= 22.5 kNm
Bending moment in (2-3)
B.m 2 = 20x + 5x (x/2)
(c) Calculate the bending moment at 1m intervals along the beam.
Bending moment in (1-2) 1m long
B.m 1 = 20x + 5x(x/2)
B.m 1 = 0
B,m 2 = 20(1) + 5(1)(1/2)
= 20 + 2.5
= 22.5 kNm
Bending moment in (2-3)
B.m 2 = 20x + 5x (x/2)

Engineering Systems 6
(x=1)
B.m 2 = 20(1) + 5/2
= 22.5 kNm
(x = 2)
B.m 3 = 20x2 + 5(2)
= 40 + 10
= 50 kNm
Bending moment (3-4)
B. m x = 20x – 160/3(x - 2) + (5x)(x/2)
(x=2)
B.m 3 = 20(2) – 160/3(2-2) + 5(2)
= 10 + 10
= 50kNm
(x = 3)
B.m 4 = 20(3) – 160/3 (3-2) + 5(3)(3/2)
= 60 – 160/3 + 5x1.5
= 29.16 kNm
For 3-4, 4-5, 5-6, 6-7, and 7-8, Bending moment equation is the same
B.m x = 20x – 160/3 (x-2) + 5(x)(x/2)
(x=4)
B.m 5 = 20(4) – 160/3(2) + 5(4)(4/2)
= 80 – 320/3 + 40
= 66.67 kNm
(x=1)
B.m 2 = 20(1) + 5/2
= 22.5 kNm
(x = 2)
B.m 3 = 20x2 + 5(2)
= 40 + 10
= 50 kNm
Bending moment (3-4)
B. m x = 20x – 160/3(x - 2) + (5x)(x/2)
(x=2)
B.m 3 = 20(2) – 160/3(2-2) + 5(2)
= 10 + 10
= 50kNm
(x = 3)
B.m 4 = 20(3) – 160/3 (3-2) + 5(3)(3/2)
= 60 – 160/3 + 5x1.5
= 29.16 kNm
For 3-4, 4-5, 5-6, 6-7, and 7-8, Bending moment equation is the same
B.m x = 20x – 160/3 (x-2) + 5(x)(x/2)
(x=4)
B.m 5 = 20(4) – 160/3(2) + 5(4)(4/2)
= 80 – 320/3 + 40
= 66.67 kNm
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Engineering Systems 7
(x=5)
B. m 6 = 20(5) – 160/3(5-2) + 5(5)(5/2)
= 62.5 kNm
(x=6)
B.m 7 = 20(6) – 160/3(6-2) + 5(7)(7/2)
= -4.167kNm
Bending moment (8-9)
B.m x = 20x – 160/3 (x-2) + 10(x-7) + 5x(x/2)
(x=7)
B.m 8 = 20(7) – 160/3(5) + 0 + 5(7)(7/2)
= -4.167
(x = 8)
B.m 9 = 20(8) – 160/3(8-2) + 10(8-7) + 5(8)(8/2)
= 160 – 160/3 x 6 + 10 + 160
= 10kNm
Bending moment (9-10)
B.m x = 20x – 160/3(x*2) + 5x(x/2) – 80/3(x-8)
(x= 8)
B. m 9 = 10kNm
(x= 9)
B.m 10 = 2x9 – 160/3(7) + 20 + 5x81/2 – 80/3(1)
= 2.5kNm
(x=10)
(x=5)
B. m 6 = 20(5) – 160/3(5-2) + 5(5)(5/2)
= 62.5 kNm
(x=6)
B.m 7 = 20(6) – 160/3(6-2) + 5(7)(7/2)
= -4.167kNm
Bending moment (8-9)
B.m x = 20x – 160/3 (x-2) + 10(x-7) + 5x(x/2)
(x=7)
B.m 8 = 20(7) – 160/3(5) + 0 + 5(7)(7/2)
= -4.167
(x = 8)
B.m 9 = 20(8) – 160/3(8-2) + 10(8-7) + 5(8)(8/2)
= 160 – 160/3 x 6 + 10 + 160
= 10kNm
Bending moment (9-10)
B.m x = 20x – 160/3(x*2) + 5x(x/2) – 80/3(x-8)
(x= 8)
B. m 9 = 10kNm
(x= 9)
B.m 10 = 2x9 – 160/3(7) + 20 + 5x81/2 – 80/3(1)
= 2.5kNm
(x=10)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Engineering Systems 8
B.m 11 = 20x10 – 160/3x8 + 30 + 5x100/2 – 80/3x2
= 200 + 30 + 250 – 100x9/3
= 480-480
= 0
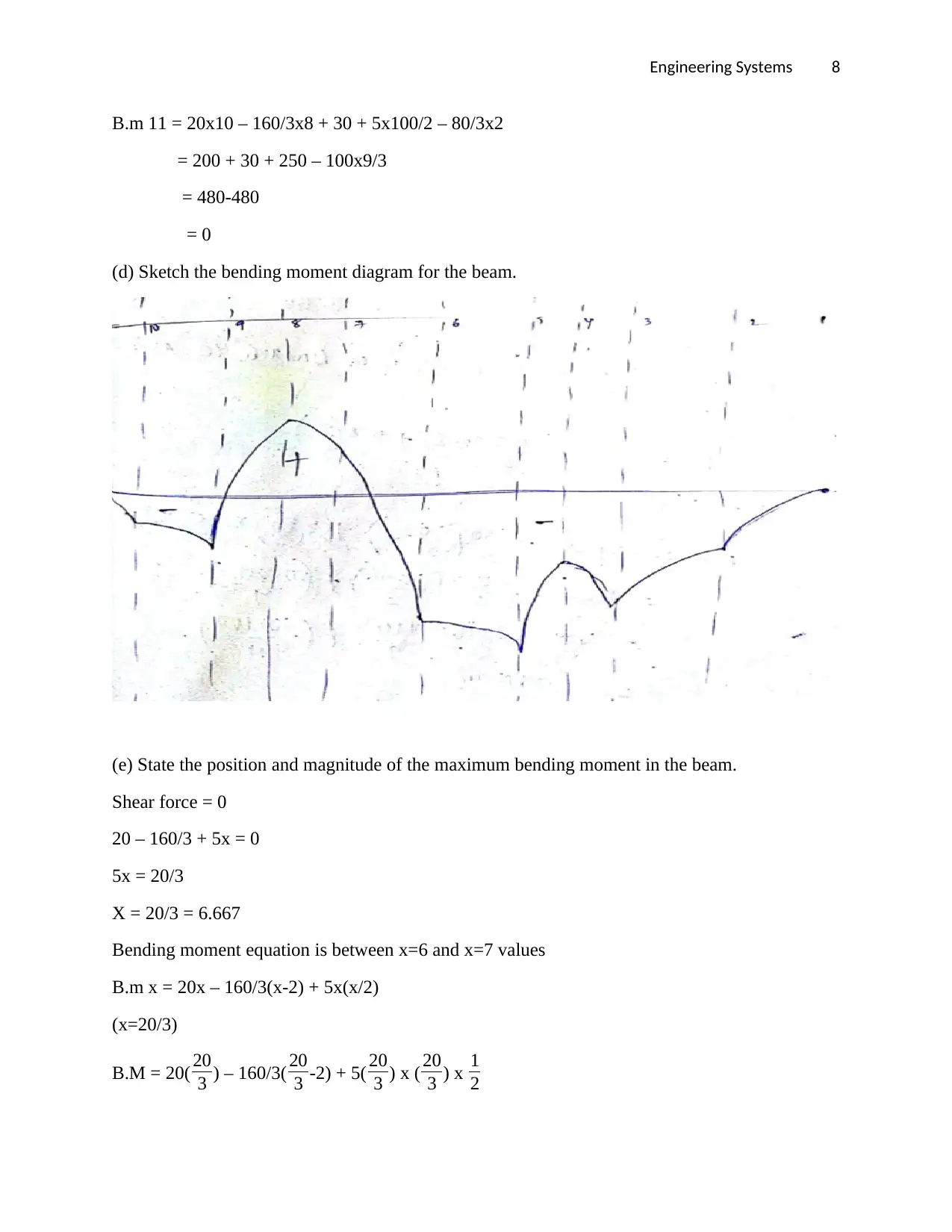
(d) Sketch the bending moment diagram for the beam.
(e) State the position and magnitude of the maximum bending moment in the beam.
Shear force = 0
20 – 160/3 + 5x = 0
5x = 20/3
X = 20/3 = 6.667
Bending moment equation is between x=6 and x=7 values
B.m x = 20x – 160/3(x-2) + 5x(x/2)
(x=20/3)
B.M = 20( 20
3 ) – 160/3( 20
3 -2) + 5( 20
3 ) x ( 20
3 ) x 1
2
B.m 11 = 20x10 – 160/3x8 + 30 + 5x100/2 – 80/3x2
= 200 + 30 + 250 – 100x9/3
= 480-480
= 0
(d) Sketch the bending moment diagram for the beam.
(e) State the position and magnitude of the maximum bending moment in the beam.
Shear force = 0
20 – 160/3 + 5x = 0
5x = 20/3
X = 20/3 = 6.667
Bending moment equation is between x=6 and x=7 values
B.m x = 20x – 160/3(x-2) + 5x(x/2)
(x=20/3)
B.M = 20( 20
3 ) – 160/3( 20
3 -2) + 5( 20
3 ) x ( 20
3 ) x 1
2

Engineering Systems 9
= 400/3 – 160x14/9 + 10x100/9
= 68.5kNm
A beam of rectangular cross section 200 mm deep and 100 mm wide. If the beam is 3m long,
simply supported at either end and carries point loads as shown in FIGURE 2 (on page 4)
(a) Calculate the maximum bending moment
R1 + R2 = 15
R2 x 3 = 5 + (10 x 2)
R2 = 25/3
R1 = 15 – 25/3 = 20/3 kN
Bending moment at A = 0
B = 20/3 kNm
C = (20/3 x 2) – 5
= 8.33 kNm
The maximum bending moment = 8.33 kNm
(b) Calculate the maximum stress in the beam
Bending stress = 8.33 x (200/[100x2])2/{0.1x0.23/12}
= 12.49 mPa
(c) At the point of maximum stress sketch a graph of the stress distribution through the thickness
of the beam, indicating which tensile and compressive stresses are.
= 400/3 – 160x14/9 + 10x100/9
= 68.5kNm
A beam of rectangular cross section 200 mm deep and 100 mm wide. If the beam is 3m long,
simply supported at either end and carries point loads as shown in FIGURE 2 (on page 4)
(a) Calculate the maximum bending moment
R1 + R2 = 15
R2 x 3 = 5 + (10 x 2)
R2 = 25/3
R1 = 15 – 25/3 = 20/3 kN
Bending moment at A = 0
B = 20/3 kNm
C = (20/3 x 2) – 5
= 8.33 kNm
The maximum bending moment = 8.33 kNm
(b) Calculate the maximum stress in the beam
Bending stress = 8.33 x (200/[100x2])2/{0.1x0.23/12}
= 12.49 mPa
(c) At the point of maximum stress sketch a graph of the stress distribution through the thickness
of the beam, indicating which tensile and compressive stresses are.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Engineering Systems 10
(d) Determine the dimensions of the cross section which will minimize the maximum stress
value if:
• the cross sectional area of the beam can be increased by 20%
• the beam section is to remain a solid rectangle
• neither the breadth or depth of the beam section can be reduced below their original
dimensions.
120/100 x (200x100) = 2400mm2
b x d = 2400mm2
b =100mm and d = 240mm
y=120mm
I = (100x2403)/3 = 115.2 x106 mm4
F1 = 25/3 x 103 x 103 x120/(115.2 x106)
= 8.68 MPa
(e) Determine the percentage reduction of the maximum stress value when the new cross section
is used.
% Reduction of fmax = (12.5 – 8.68)/12.5 x 100
= 30.5%
(d) Determine the dimensions of the cross section which will minimize the maximum stress
value if:
• the cross sectional area of the beam can be increased by 20%
• the beam section is to remain a solid rectangle
• neither the breadth or depth of the beam section can be reduced below their original
dimensions.
120/100 x (200x100) = 2400mm2
b x d = 2400mm2
b =100mm and d = 240mm
y=120mm
I = (100x2403)/3 = 115.2 x106 mm4
F1 = 25/3 x 103 x 103 x120/(115.2 x106)
= 8.68 MPa
(e) Determine the percentage reduction of the maximum stress value when the new cross section
is used.
% Reduction of fmax = (12.5 – 8.68)/12.5 x 100
= 30.5%
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Engineering Systems 11
3. A column has the dimensions shown in the diagram below.
(a) What is the minimum length of the column at which buckling is likely to occur?
Young’s Modulus, E = 200GN/m2
Yield Stress, σ = 140 MN/m2
Di = 60mm
Do = 30mm
Moment of Inertia, I = π
64 (D04 – DL4) = 1.37 x 10-6
Cross Section Area, A = π
4 (D02 – DL2) = 2.2 x 10-3
Le =L/2
140 x 106 = π 2 x 200 x 109 x 1.37 x 10−6
2.2 x 10−3 x (l/2)2
L = 5.926m
(b) If the column is the length determined in (a),
(i) What will be the mode of failure?
The mode of failure will be compressive stress or crushing failure
(ii) At what load would you expect failure to occur?
P = π 2 EI
L2 = π 2 x 200 x 109 x 1.37 x 10−6
(2.963) 2
3. A column has the dimensions shown in the diagram below.
(a) What is the minimum length of the column at which buckling is likely to occur?
Young’s Modulus, E = 200GN/m2
Yield Stress, σ = 140 MN/m2
Di = 60mm
Do = 30mm
Moment of Inertia, I = π
64 (D04 – DL4) = 1.37 x 10-6
Cross Section Area, A = π
4 (D02 – DL2) = 2.2 x 10-3
Le =L/2
140 x 106 = π 2 x 200 x 109 x 1.37 x 10−6
2.2 x 10−3 x (l/2)2
L = 5.926m
(b) If the column is the length determined in (a),
(i) What will be the mode of failure?
The mode of failure will be compressive stress or crushing failure
(ii) At what load would you expect failure to occur?
P = π 2 EI
L2 = π 2 x 200 x 109 x 1.37 x 10−6
(2.963) 2

Engineering Systems 12
= 308kN
(c) If the column is half the length determined in (a)
L = l/2 = 5.926/2 = 2.963m
(i) What will be the mode of failure?
σc = π2 EI
A L 2 = π 2 x 200 x 109 x 1.37 x 10−6
2.2 x 10−3 x (2.963/2)2
= 560 MN/m2
Since σc > σy
Failure will occur through compressive stress or crushing only
(ii) At what load would you expect failure to occur?
Load, P = π 2 EI
Le2 = π 2 x 200 x 109 x 1.37 x 10−6
(1.4815)2
P = 1232.1 kN
= 308kN
(c) If the column is half the length determined in (a)
L = l/2 = 5.926/2 = 2.963m
(i) What will be the mode of failure?
σc = π2 EI
A L 2 = π 2 x 200 x 109 x 1.37 x 10−6
2.2 x 10−3 x (2.963/2)2
= 560 MN/m2
Since σc > σy
Failure will occur through compressive stress or crushing only
(ii) At what load would you expect failure to occur?
Load, P = π 2 EI
Le2 = π 2 x 200 x 109 x 1.37 x 10−6
(1.4815)2
P = 1232.1 kN
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 13
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





