ME1300 Statics Assignment: Engineering Systems & Static Equilibrium
VerifiedAdded on 2023/06/15
|7
|897
|359
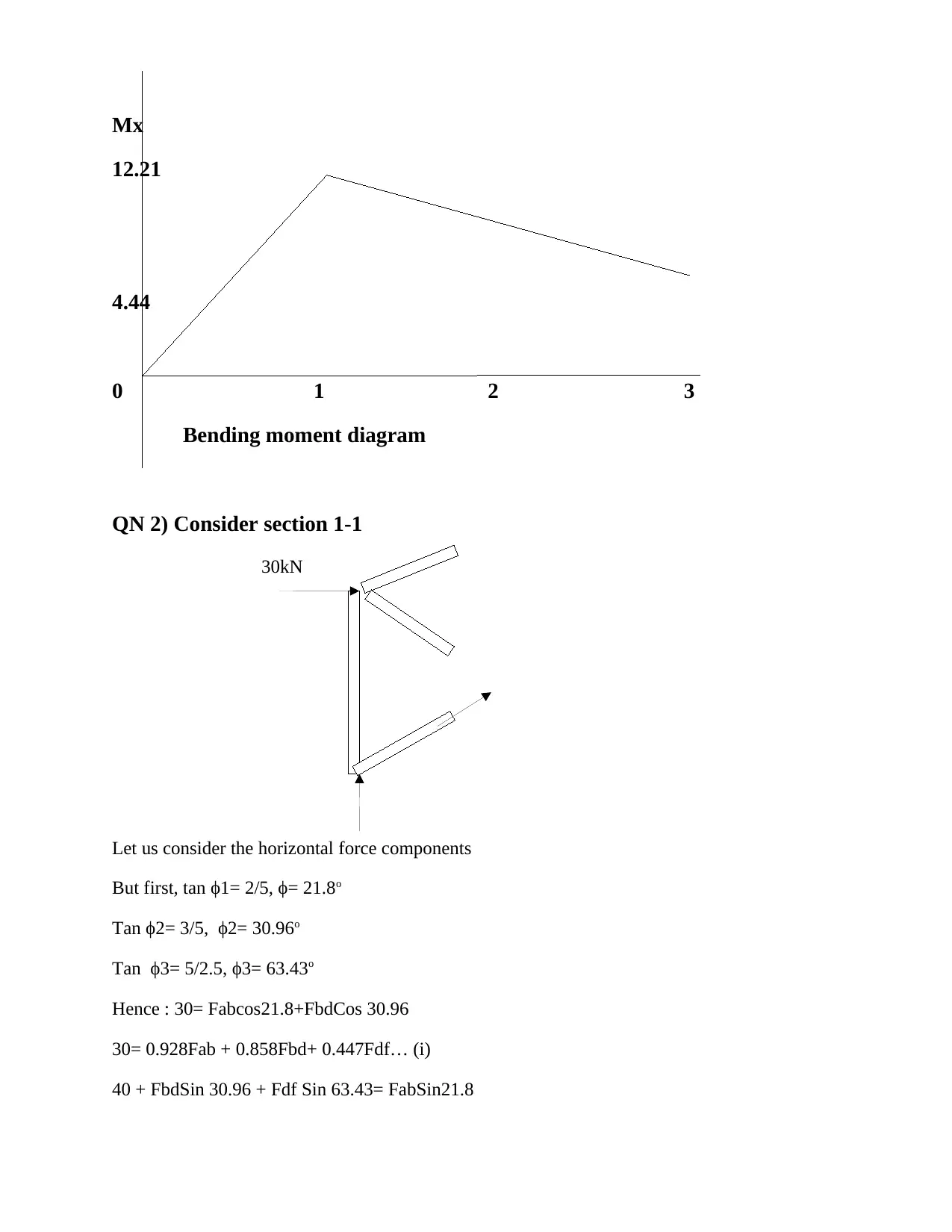
Homework Assignment
AI Summary
This document provides solutions to a statics assignment involving the analysis of engineering structures under static loads. It covers concepts such as free body diagrams, equilibrium equations, and the application of mathematical and engineering science methods to solve problems. The assignment includes questions related to clamping forces, reactions at hinges, strut forces, bending moment calculations, and shear force diagrams. Specific problems address the determination of reactions at supports, shear force and bending moment equations, and the analysis of forces in structural members. The solutions involve detailed calculations and explanations, demonstrating an understanding of static equilibrium principles and their application to engineering scenarios. Desklib provides a platform for students to access similar solved assignments and past papers for academic support.
1 out of 7









![[object Object]](/_next/static/media/star-bottom.7253800d.svg)