Statistical Analysis for Desklib

This text provides statistical analysis for various scenarios including hypothesis testing, ANOVA, t-tests and more. It explains the significance of p-value and critical values and how to draw conclusions from data.

STATISTICS
STUDENT NAME/ID
[Pick the date]

Question 1
(a) Null hypothesis H0: Hair colour and regional promotions are independent.
(b) Alternative hypothesis H1: Hair colour and regional promotions are dependent.
(c) The Type I error for this test is 5% which implies that there is a 0.05 probability that a true
null hypothesis may be rejected. This implies that even if statistical analysis suggests that the
complaints are valid, there is a 5% chance that the complaints may not be valid and the same
needs to be considered.
(d) The Type II error for this test would refer to a situation when the null hypothesis is indicated
to be true when it is false. For the company, it would describe a situation when even though
the allegations or complaints may be rejected but they may be valid. Hence, this error needs
to be minimised.
(e) Critical value of the test statistic
Chi square test statistic would be appropriate measured for the present case.
Degree of freedom = (n-1) (r-1) = (4– 1) (6-1) = 15
Level of significance = 0.05
The critical value of the chi square statistic = 24.9957
(f) The calculated value of test statistic
1

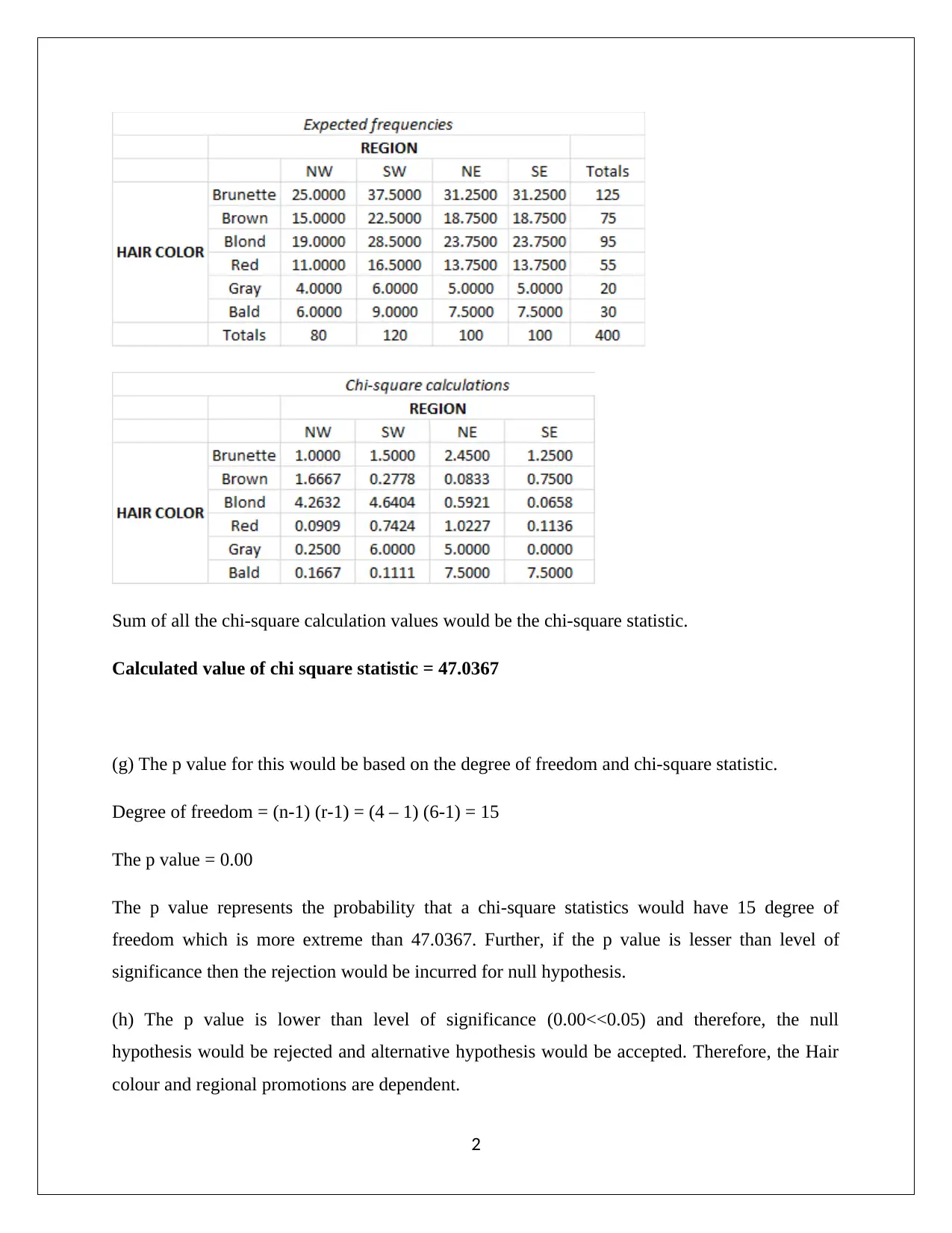
Sum of all the chi-square calculation values would be the chi-square statistic.
Calculated value of chi square statistic = 47.0367
(g) The p value for this would be based on the degree of freedom and chi-square statistic.
Degree of freedom = (n-1) (r-1) = (4 – 1) (6-1) = 15
The p value = 0.00
The p value represents the probability that a chi-square statistics would have 15 degree of
freedom which is more extreme than 47.0367. Further, if the p value is lesser than level of
significance then the rejection would be incurred for null hypothesis.
(h) The p value is lower than level of significance (0.00<<0.05) and therefore, the null
hypothesis would be rejected and alternative hypothesis would be accepted. Therefore, the Hair
colour and regional promotions are dependent.
2

(i) It is apparent that regional promotions seem to be linked to colour and hence a thorough
review of these promotions need to be conducted with focus on performance so as to make
necessary changes. Also, a strict action must be taken against those managers who have
discriminated.
Question 2
(a) Null hypothesis H0: Distribution of demographics of total sales force and regional
promotions are independent.
(b) Alternative hypothesis H1: Distribution of demographics of total sales force and regional
promotions are dependent.
(c) The Type I error for this test is 5% which implies that there is a 0.05 probability that a true
null hypothesis may be rejected. This implies that even if statistical analysis suggests that
discrimination has been observed, there is a 5% chance that the company should not be
accused by ACLU with regards to practising discrimination.
(d) The Type II error for this test would refer to a situation when the null hypothesis is indicated
to be true when it is false. For the company, it would describe a situation when even though
the allegations or complaints may be rejected but they may be valid. As a result, the company
should conduct an internal enquiry even if ACLU rejects the discrimination charges.
(e) Expected number of promotions
Expected frequency
Total number of promotions = 400
3

(f) Critical value of test statistic
Chi square test statistic would be appropriate measured for the present case.
Degree of freedom = (n-1) (r-1) = (2 – 1) (6-1) = 5
Level of significance = 0.05
The critical value of the chi square statistic = 11.070
(g) Calculated value of test statistic
Calculated value of chi square statistic = 0.2948
(h) The p value for this would be based on the degree of freedom and chi-square statistic.
Degree of freedom = (n-1) (r-1) = (2 – 1) (6-1) = 5
The p value = 0.997
The p value represents the probability that a chi-square statistics would have 5 degree of freedom
which does not exceed than 0.2948. Further, if the p value is lesser than level of significance then
the rejection would be incurred for null hypothesis.
4

(i) The p value is higher than level of significance (0.997<<0.05) and therefore, the null
hypothesis would not be rejected and alternative hypothesis would not be accepted.
Therefore, distribution of demographics of total sales force and regional promotions are
independent.
(j) Based on the above, it is apparent that no action is required to be undertaken with regards to
regional promotions being biased. However, considering the possibility of Type II error, any
future allegation in this regards should be looked into promptly.
Question 3
(a) Null hypothesis H0: Quarterly sales and region are independent.
(b) Alternative hypothesis H1: Quarterly sales and region are dependent.
(c) The Type I error for this test is 5% which implies that there is a 0.05 probability that a true
null hypothesis may be rejected. This implies that even if the statistical analysis indicates that
the quarterly sales are determined by region, the same should be verified with additional
measures such as pilot studies.
(d) The Type II error for this test would refer to a situation when the null hypothesis is indicated
to be true when it is false. For the company, it would describe a situation when even though
statistical analysis may indicate no relation between region and sales, but still such a
relationship may exist and thus the company should be receptive to the idea if any favourable
data does arise.
(e) Critical value of test statistic
Chi square test statistic would be appropriate measured for the present case.
Degree of freedom = (n-1) (r-1) = (4 – 1) (4-1) = 9
Level of significance = 0.05
The critical value of the chi square statistic = 16.9189
(f) The calculated value of test statistic
5

Sum of all the chi-square calculation values would be the chi-square statistic.
Chi Square statistic = 3.2510
(g) The p value for this would be based on the degree of freedom and chi-square statistic.
Degree of freedom = (n-1) (r-1) = (4 – 1) (4-1) = 9
The p value = 0.9535
The p value represents the probability that a chi-square statistics would have 9 degree of freedom
which is more extreme than 3.2510. Further, if the p value is lesser than level of significance
then the rejection would be incurred for null hypothesis.
6

(k) The p value is higher than level of significance (0.9535>0.05) and therefore, the null
hypothesis would not be rejected and thus, alternative hypothesis would not be accepted.
Therefore, Quarterly sales and region are independent.
(l) Since, no particular region makes a higher contribution to quarterly sales, hence all the
regions should be given equal importance by the Vice President in terms of resources and
attention.
(j) The two regions that are most likely to be different are NE and SE.
Question 4
(a) Null hypothesis H0: μMewtwo=μMew
(b) Alternative hypothesis H1: μMewtwo< μMew
(c) The two sample t test for equal variance is the appropriate test to check the validity of the
claim.
(d) The Type I error for this test is 5% which implies that there is a 0.05 probability that a true
null hypothesis may be rejected Hence, this highlights that even though statistical analysis
may suggest that Mewtwo is the tougher opponent, but there is a 5% chance that the
conclusion drawn is incorrect.
(e) The Type II error for this test would refer to a situation when the null hypothesis is indicated
to be true when it is false. Thus, it might be possible that even though it might be indicated
that Mewtwo is not the tougher opponent, it is possible that this is indeed the case.
(f) Rejection region can be computed using the critical value. Considering the given
information, the rejection region would be for t<-1.68.
(g) Test statistic (for right tailed hypothesis test)
7

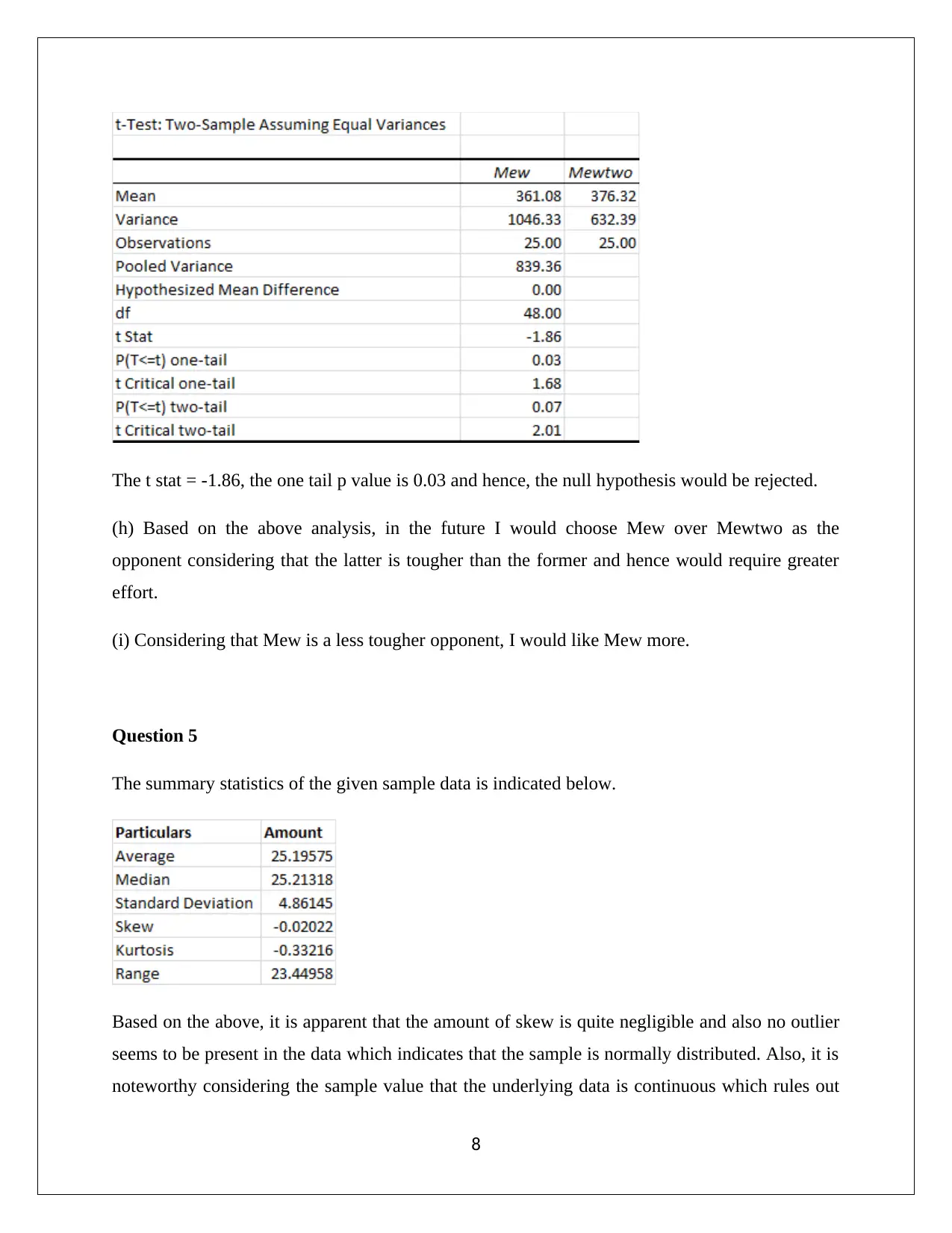
The t stat = -1.86, the one tail p value is 0.03 and hence, the null hypothesis would be rejected.
(h) Based on the above analysis, in the future I would choose Mew over Mewtwo as the
opponent considering that the latter is tougher than the former and hence would require greater
effort.
(i) Considering that Mew is a less tougher opponent, I would like Mew more.
Question 5
The summary statistics of the given sample data is indicated below.
Based on the above, it is apparent that the amount of skew is quite negligible and also no outlier
seems to be present in the data which indicates that the sample is normally distributed. Also, it is
noteworthy considering the sample value that the underlying data is continuous which rules out
8

discrete probability distributions such as binomial and discrete. Thus, with reasonable confidence
it can be stated that the underlying population is highly likely to be normally distributed only.
Question 6
(a) Null Hypothesis μ2007−μ2008=0
Alternative hypothesis: μ2007−μ2008 ≠ 0
Assuming level of significance = 0.05
The p value is lower than level of significance and hence, reject null hypothesis and hence,
sufficient evidence are present to conclude that market peaked in 2007 as compared with in
2008.
(b) In 2010 the market had returned to 2006
Null Hypothesis μ2010−μ2006=0
Alternative hypothesis: μ2010−μ2006 ≠ 0
9

Assuming level of significance = 0.05
The p value is lower than level of significance and hence, reject null hypothesis and hence,
sufficient evidence are present to conclude that market peaked in 2010 as compared with in
2006.
 In 2011 the market had returned to 2006
Null Hypothesis μ2011−μ2006=0
Alternative hypothesis: μ2011−μ2006 ≠ 0
10

Assuming level of significance = 0.05
The p value is higher than level of significance and hence, cannot reject null hypothesis and
hence, sufficient evidence are not present to conclude that market peaked in 2011 as compared
with in 2006.
(c) Market increase from 1995 to 2007
Null Hypothesis μ2011−μ1995=0
Alternative hypothesis: μ2007 > μ1995
11

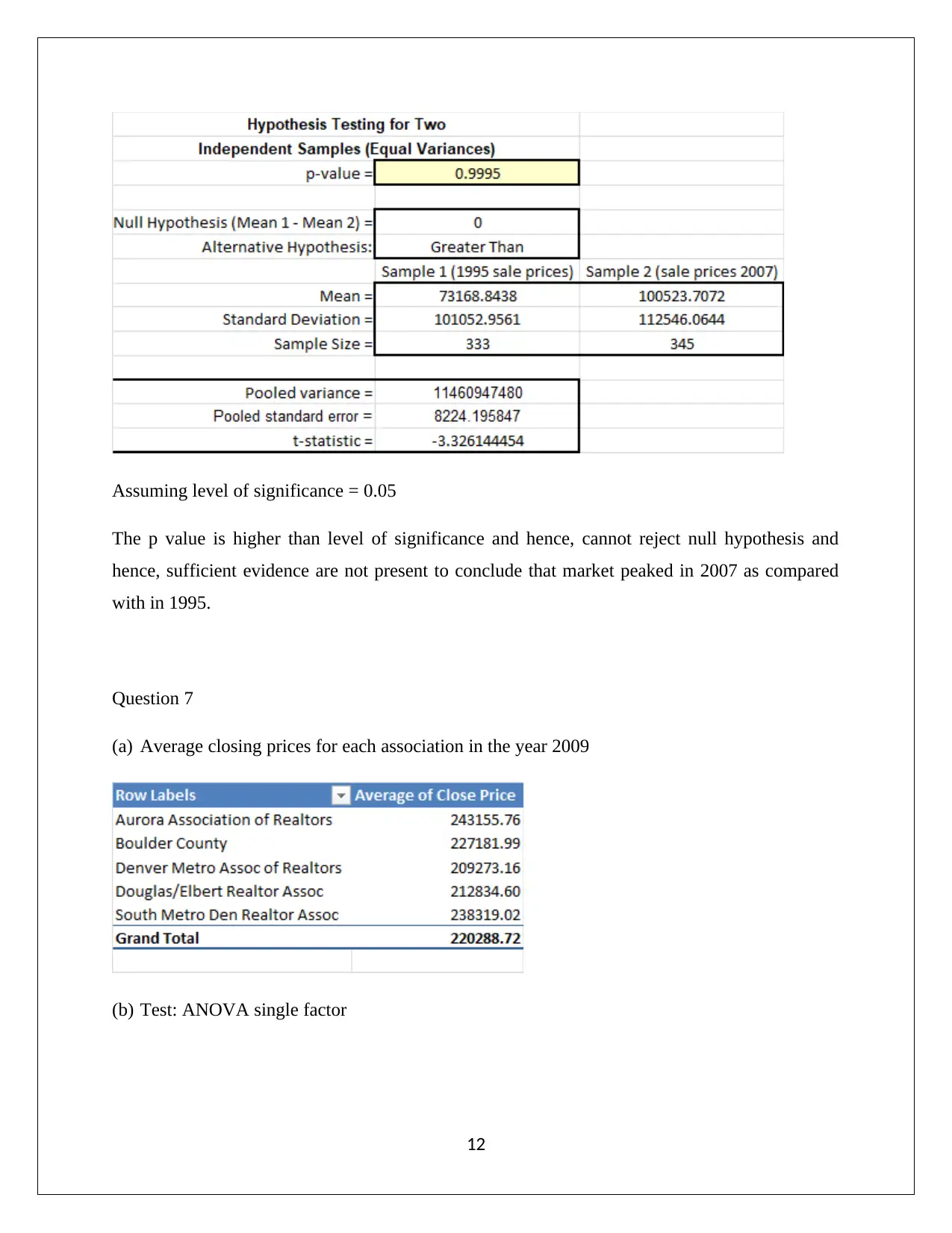
Assuming level of significance = 0.05
The p value is higher than level of significance and hence, cannot reject null hypothesis and
hence, sufficient evidence are not present to conclude that market peaked in 2007 as compared
with in 1995.
Question 7
(a) Average closing prices for each association in the year 2009
(b) Test: ANOVA single factor
12

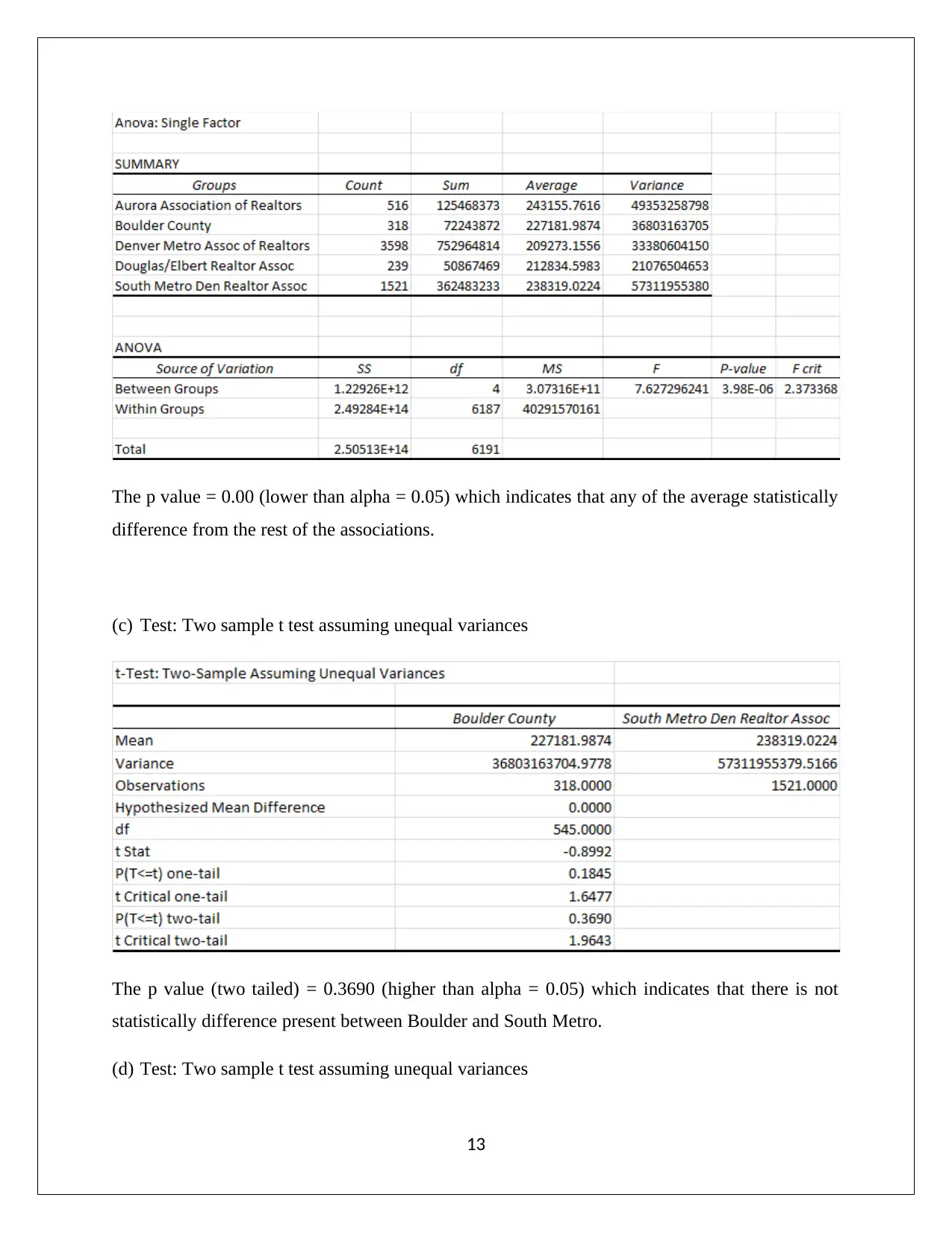
The p value = 0.00 (lower than alpha = 0.05) which indicates that any of the average statistically
difference from the rest of the associations.
(c) Test: Two sample t test assuming unequal variances
The p value (two tailed) = 0.3690 (higher than alpha = 0.05) which indicates that there is not
statistically difference present between Boulder and South Metro.
(d) Test: Two sample t test assuming unequal variances
13

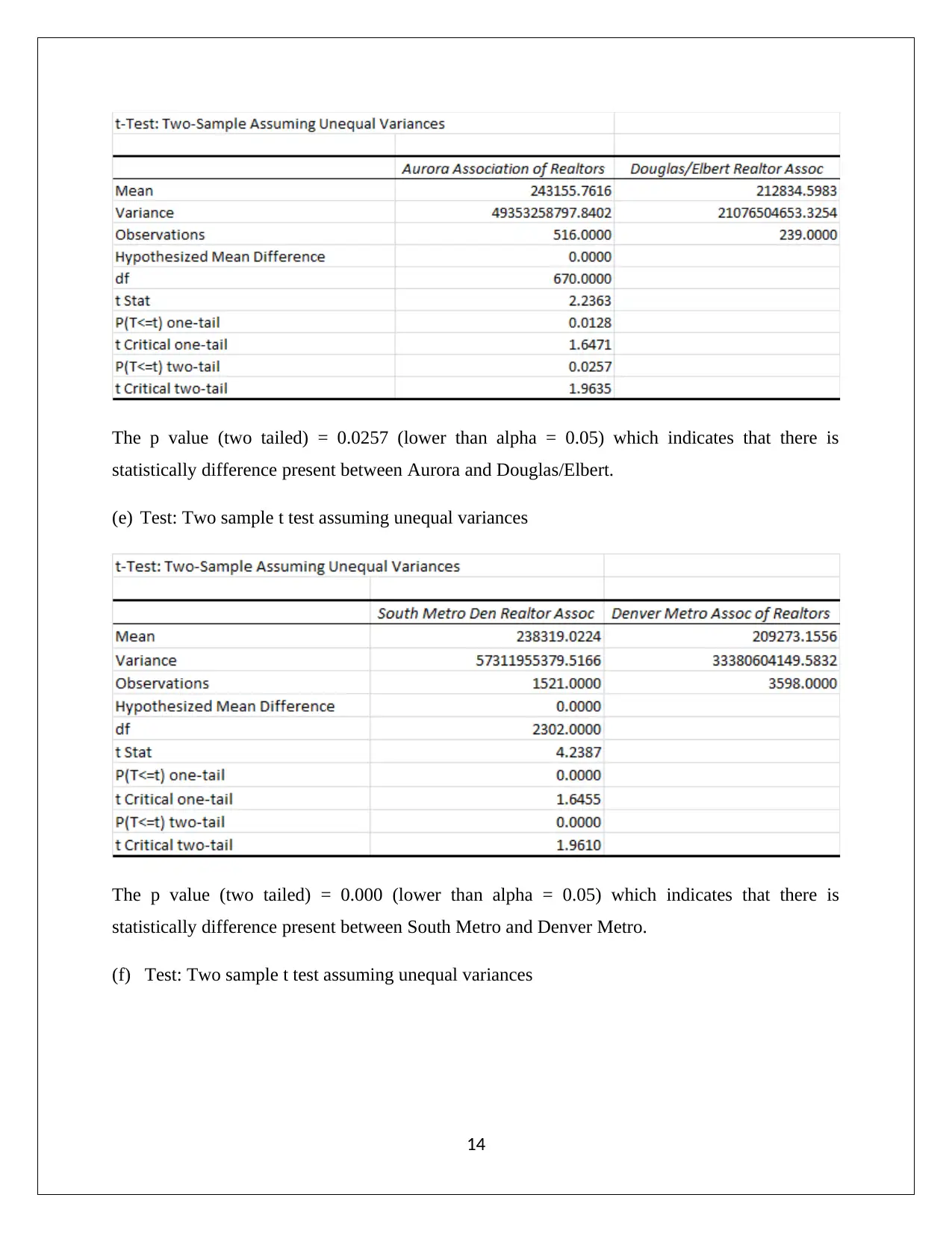
The p value (two tailed) = 0.0257 (lower than alpha = 0.05) which indicates that there is
statistically difference present between Aurora and Douglas/Elbert.
(e) Test: Two sample t test assuming unequal variances
The p value (two tailed) = 0.000 (lower than alpha = 0.05) which indicates that there is
statistically difference present between South Metro and Denver Metro.
(f) Test: Two sample t test assuming unequal variances
14

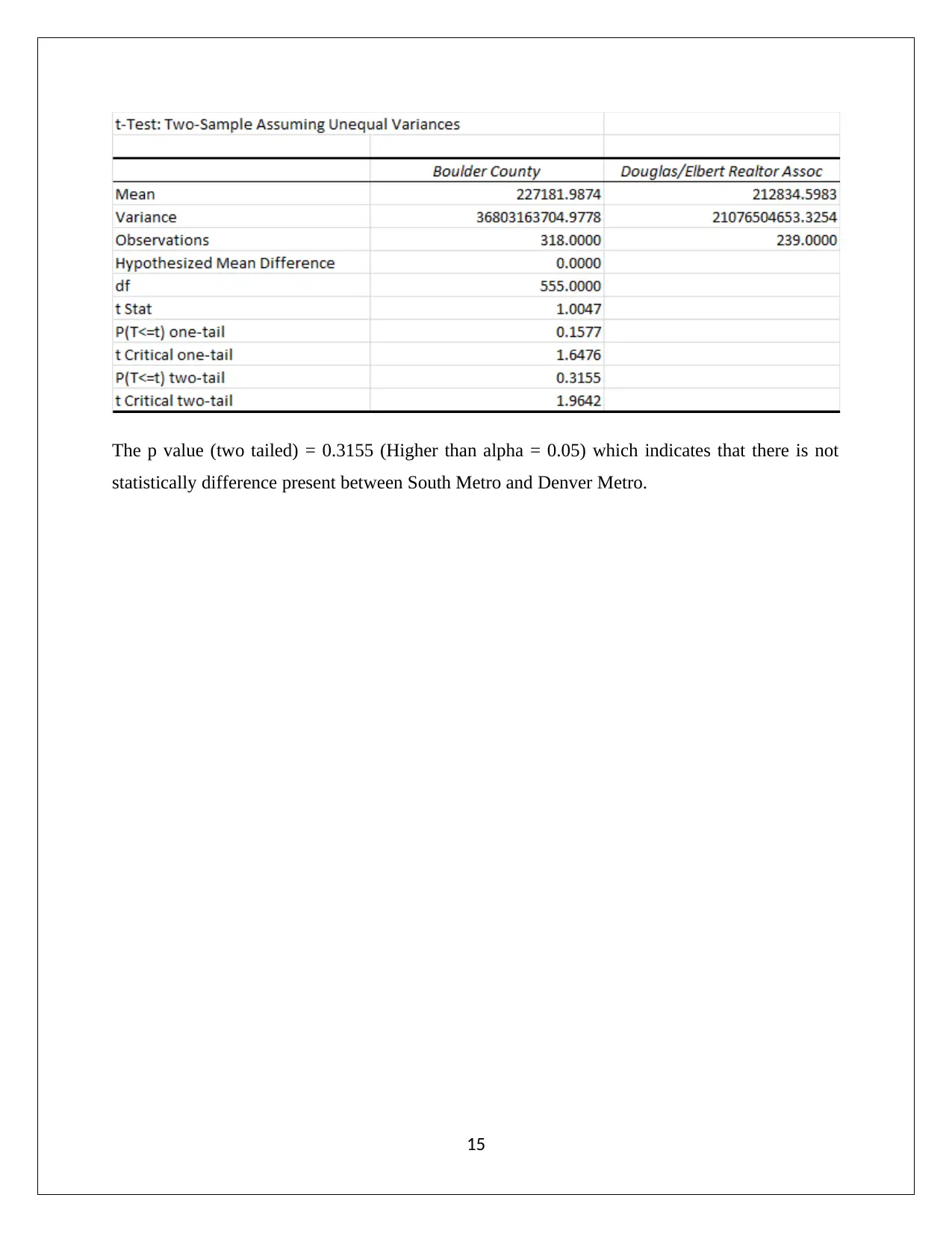
The p value (two tailed) = 0.3155 (Higher than alpha = 0.05) which indicates that there is not
statistically difference present between South Metro and Denver Metro.
15