Fuel Price Statistical Analysis Project Part C: MAT10251 Data
VerifiedAdded on 2023/06/03
|15
|2521
|395
Project
AI Summary
This assignment presents a statistical analysis of fuel price data, focusing on diesel and unleaded 91 prices in Queensland, Australia. It includes a hypothesis test to determine if there's a significant difference in diesel prices between regional cities and Brisbane, using a Z-test. Simple linear regression is employed to explore the relationship between unleaded 91 and diesel prices, with diesel price as the independent variable. Further, a multiple linear regression model incorporates location as a second independent variable to predict unleaded 91 prices, demonstrating an improved model fit compared to the simple linear regression. Appendices provide detailed statistical answers and justifications for the methods used, including assumptions, variable definitions, and interpretations of regression coefficients and correlation coefficients.

MAT10251 STATISTICAL ANALYSIS
Data Analysis Project – Part C
Please Include Part C Coversheet
1
Data Analysis Project – Part C
Please Include Part C Coversheet
1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Question 1: Statistical Inference Topic 7
Oz-Fuel-Watch wished to know if, on 1st August 2018, the mean the price of Diesel was less
in the capital city Brisbane, or elsewhere in the regional states.
Data was obtained from the petrol pumps in Queensland, both from regional and capital-
Brisbane areas in a random sample of 80 pumps. The sample consisted of 38 petrol pumps
from regional areas and 42 pumps from capital- Brisbane.
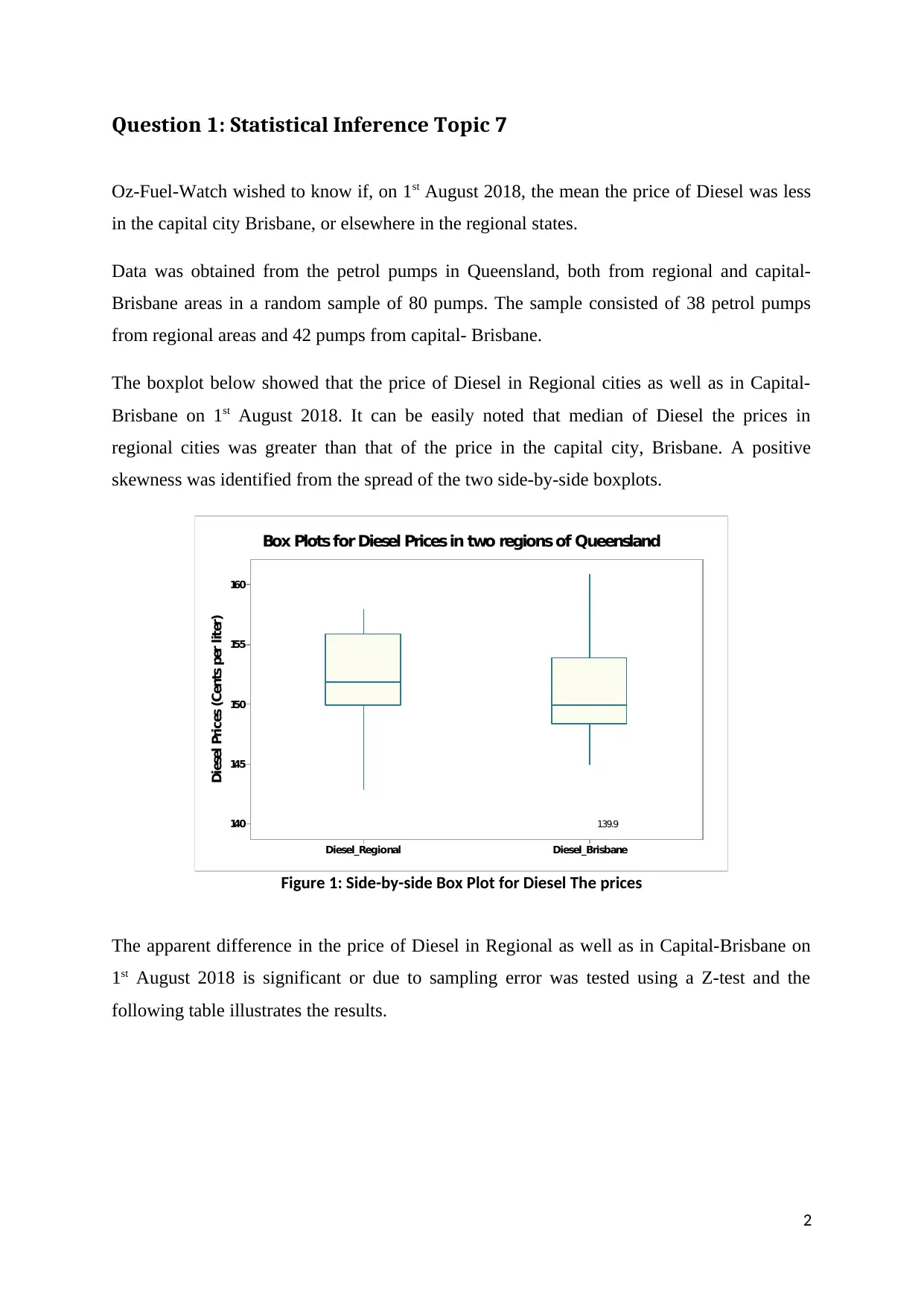
The boxplot below showed that the price of Diesel in Regional cities as well as in Capital-
Brisbane on 1st August 2018. It can be easily noted that median of Diesel the prices in
regional cities was greater than that of the price in the capital city, Brisbane. A positive
skewness was identified from the spread of the two side-by-side boxplots.
Diesel_BrisbaneDiesel_Regional
160
155
150
145
140
Diesel Prices (Cents per liter)
139.9
Box Plots for Diesel Prices in two regions of Queensland
Figure 1: Side-by-side Box Plot for Diesel The prices
The apparent difference in the price of Diesel in Regional as well as in Capital-Brisbane on
1st August 2018 is significant or due to sampling error was tested using a Z-test and the
following table illustrates the results.
2
Oz-Fuel-Watch wished to know if, on 1st August 2018, the mean the price of Diesel was less
in the capital city Brisbane, or elsewhere in the regional states.
Data was obtained from the petrol pumps in Queensland, both from regional and capital-
Brisbane areas in a random sample of 80 pumps. The sample consisted of 38 petrol pumps
from regional areas and 42 pumps from capital- Brisbane.
The boxplot below showed that the price of Diesel in Regional cities as well as in Capital-
Brisbane on 1st August 2018. It can be easily noted that median of Diesel the prices in
regional cities was greater than that of the price in the capital city, Brisbane. A positive
skewness was identified from the spread of the two side-by-side boxplots.
Diesel_BrisbaneDiesel_Regional
160
155
150
145
140
Diesel Prices (Cents per liter)
139.9
Box Plots for Diesel Prices in two regions of Queensland
Figure 1: Side-by-side Box Plot for Diesel The prices
The apparent difference in the price of Diesel in Regional as well as in Capital-Brisbane on
1st August 2018 is significant or due to sampling error was tested using a Z-test and the
following table illustrates the results.
2

Table 1: Z Test for Differences in Two Means
From the p-value, the probability that there was any difference in Diesel the prices between
the regional cities and the capital city Brisbane was 0.18. That is a realistic and likely event.
Hence, the sample provides no evidence that there was an actual difference in the average the
prices of Diesel between regional cities and the capital city on 1st August 2018. So, motorists
who bought Diesel from either a regional or the capital city paid approximately same the
price for his or her fuel.
3
From the p-value, the probability that there was any difference in Diesel the prices between
the regional cities and the capital city Brisbane was 0.18. That is a realistic and likely event.
Hence, the sample provides no evidence that there was an actual difference in the average the
prices of Diesel between regional cities and the capital city on 1st August 2018. So, motorists
who bought Diesel from either a regional or the capital city paid approximately same the
price for his or her fuel.
3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Questions 2: Simple Linear Regression
Oz-Fuel-Watch was interested in exploring the relationship between Unleaded 91 and
Diesel the prices. Expecting that Diesel the price would influence Unleaded 91 the prices,
the Diesel the price was as the independent variable and the price of Unleaded 91 as the
independent variable to predict the price of Unleaded 91 based on Diesel the prices. A
positive relationship between the two fuels was expected on 1st August 2018.
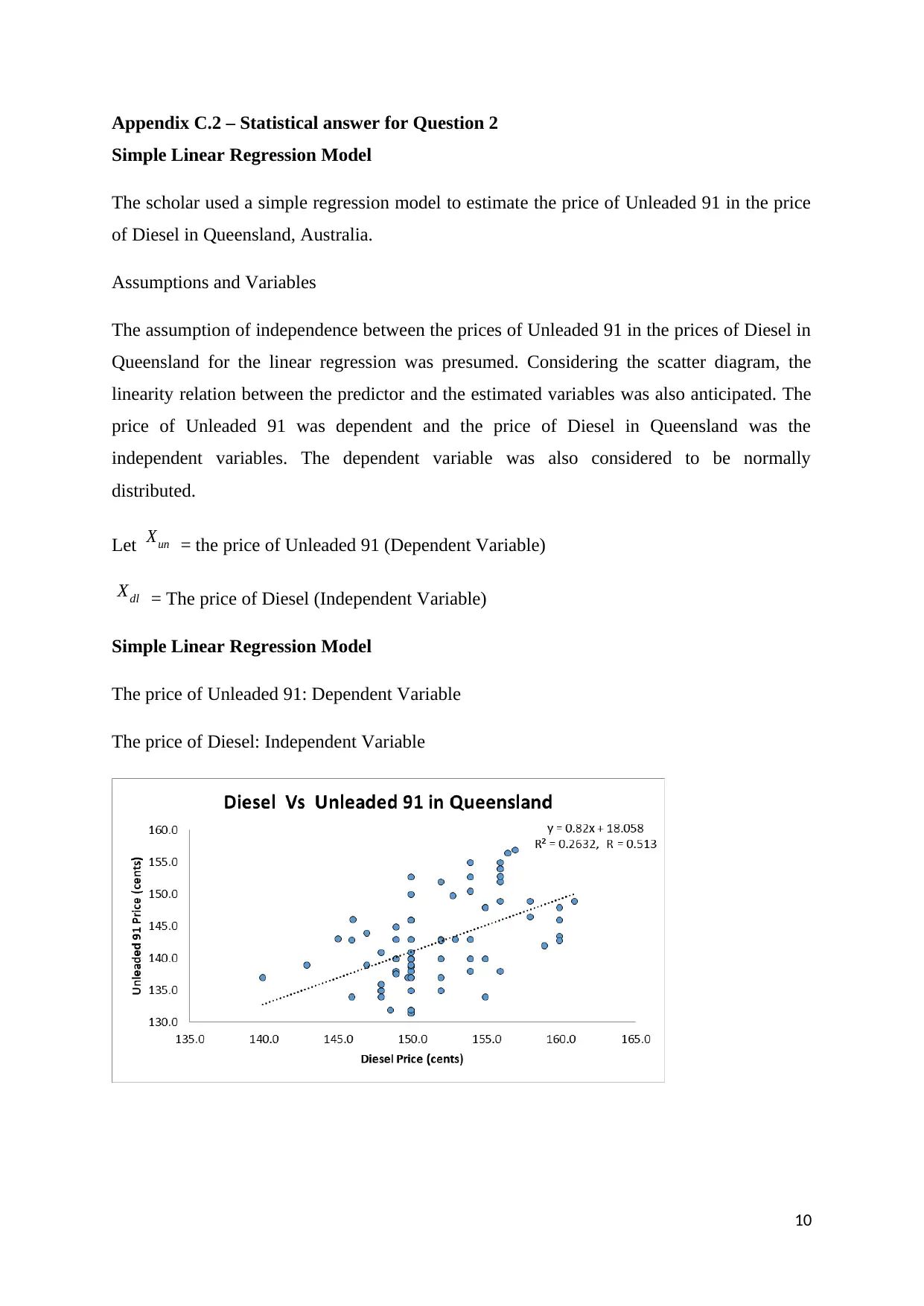
The regression equation was evaluated as Pr ice Unleaded 91=0 . 82∗Diesel Pr ice+18 .058 ,
where the correlation coefficient was 0.513 and the coefficient of determination was
evaluated to be 0.263.
As expected, the scatterplot shows that the price of Unleaded 91 was higher in cities,
where Diesel the prices were also comparatively higher than other places. However, while
this positive relationship was approximately linear it was also moderately strong. For one
cent the price increase in Diesel, then the price of Unleaded 91 was expected to increase
by 0.82 cents. Also, an initial price of 18.06 cents was identified for Unleaded 91, even if
the price of Diesel becomes zero. Therefore Unleaded 91 was expected to cost 18.06
cents even if Diesel became free in the market.
Figure 2: Scatter Plot for the prices of Unleaded 91 fuel on the prices of Diesel
4
Oz-Fuel-Watch was interested in exploring the relationship between Unleaded 91 and
Diesel the prices. Expecting that Diesel the price would influence Unleaded 91 the prices,
the Diesel the price was as the independent variable and the price of Unleaded 91 as the
independent variable to predict the price of Unleaded 91 based on Diesel the prices. A
positive relationship between the two fuels was expected on 1st August 2018.
The regression equation was evaluated as Pr ice Unleaded 91=0 . 82∗Diesel Pr ice+18 .058 ,
where the correlation coefficient was 0.513 and the coefficient of determination was
evaluated to be 0.263.
As expected, the scatterplot shows that the price of Unleaded 91 was higher in cities,
where Diesel the prices were also comparatively higher than other places. However, while
this positive relationship was approximately linear it was also moderately strong. For one
cent the price increase in Diesel, then the price of Unleaded 91 was expected to increase
by 0.82 cents. Also, an initial price of 18.06 cents was identified for Unleaded 91, even if
the price of Diesel becomes zero. Therefore Unleaded 91 was expected to cost 18.06
cents even if Diesel became free in the market.
Figure 2: Scatter Plot for the prices of Unleaded 91 fuel on the prices of Diesel
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

The correlation coefficient revealed a positive and strong relationship between the prices of
the two types of fuels. The price of diesel served as an independent variable to predict the
price of unleaded 91, and it was able to explain 26.3% variation or fluctuation in the price of
Unleaded 91. These values were in line with the trend of the scatter plot. The strength of the
relation between the variables proved out to be stronger than the scatter plot trend.
Table 2: Simple Regression Model
Question 3: Multiple Linear Regression Model Topic 9
Since the location of the pumps was also an important predictor for Unleaded 91, location
was introduced in the linear regression model as a second independent variable. The scholar
wanted to estimate the price of Unleaded 91 for petrol pumps in the capital-Brisbane,
Australia on 1st August 2006.
The following table gives the Excel output for this new model.
Table 3: Regression Statistics for Simple Linear Regression Model
The significance values or p-values were less than 0.05, for both independent variables in the
above table. This indicates that both Diesel the prices and location make a significant
5
the two types of fuels. The price of diesel served as an independent variable to predict the
price of unleaded 91, and it was able to explain 26.3% variation or fluctuation in the price of
Unleaded 91. These values were in line with the trend of the scatter plot. The strength of the
relation between the variables proved out to be stronger than the scatter plot trend.
Table 2: Simple Regression Model
Question 3: Multiple Linear Regression Model Topic 9
Since the location of the pumps was also an important predictor for Unleaded 91, location
was introduced in the linear regression model as a second independent variable. The scholar
wanted to estimate the price of Unleaded 91 for petrol pumps in the capital-Brisbane,
Australia on 1st August 2006.
The following table gives the Excel output for this new model.
Table 3: Regression Statistics for Simple Linear Regression Model
The significance values or p-values were less than 0.05, for both independent variables in the
above table. This indicates that both Diesel the prices and location make a significant
5

contribution to the model and should be included. Hence, adding location has resulted in a
stronger model.
Therefore, the Multiple Regression Model was evaluated as:
Price of Unleaded 91 = 31.91 + 0.75* Price of Diesel The price – 5.76 * Location Dummy
The coefficient of Diesel the price in this equation was 0.75, indicating that for the same
petrol pump (in a particular city), every additional cent spent in purchasing Diesel the
predicted the price of Unleaded 91 increase approximately by 0.75 cents. While the
coefficient of location (dummy) indicates that estimated the price of Unleaded 91 would
decrease by 5.76 cents if the fuel is bought from any pump in capital-Brisbane.
From the correlation coefficient the strength of the relationship was found to be moderately
strong. In particular, the coefficient of determination was 0.452, indicating that 45.2% of the
variation in the prices of Unleaded 91was explained by the variation in the price of Diesel
and location of the fuel pump. Hence, other factors, for example, the location of the pump
from where the Unleaded 91 was bought would also influence the final the price of the fuel.
The Multiple Regression Model was able to explain 45.2% variation in the price of Unleaded
91, whereas the simple regression model was able to explain 26.32% variation in fuel the
prices. Hence, the Multiple Regression Model was a better choice in estimating Unleaded 91
the prices.
6
stronger model.
Therefore, the Multiple Regression Model was evaluated as:
Price of Unleaded 91 = 31.91 + 0.75* Price of Diesel The price – 5.76 * Location Dummy
The coefficient of Diesel the price in this equation was 0.75, indicating that for the same
petrol pump (in a particular city), every additional cent spent in purchasing Diesel the
predicted the price of Unleaded 91 increase approximately by 0.75 cents. While the
coefficient of location (dummy) indicates that estimated the price of Unleaded 91 would
decrease by 5.76 cents if the fuel is bought from any pump in capital-Brisbane.
From the correlation coefficient the strength of the relationship was found to be moderately
strong. In particular, the coefficient of determination was 0.452, indicating that 45.2% of the
variation in the prices of Unleaded 91was explained by the variation in the price of Diesel
and location of the fuel pump. Hence, other factors, for example, the location of the pump
from where the Unleaded 91 was bought would also influence the final the price of the fuel.
The Multiple Regression Model was able to explain 45.2% variation in the price of Unleaded
91, whereas the simple regression model was able to explain 26.32% variation in fuel the
prices. Hence, the Multiple Regression Model was a better choice in estimating Unleaded 91
the prices.
6
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Appendix C
Appendix C1 – Statistical answer for Question 1
From the boxplots, it was also identified that there was some considerable number of petrol
pumps which sold Diesel for more than the median values, in both regional and capital city.
Hypothesis Test Difference Means Two Independent Samples
To answer Question 1 and to test whether there existed a difference in average the prices of
Diesel between regional cities and capital city Brisbane, the scholar used level of significance
of 5%.
Choice of technique
Technique: Hypothesis test for difference of two independent means
The petrol pumps in regional cities and the capital city were selected randomly. There were
no common petrol pumps in the two sub-samples. Therefore, the samples were considered to
be independent.
Random Variables
Let X R and X B denote the price of Diesel in regional and Brisbane (capital) areas.
Let μR and μB denote the average the price of Diesel in regional and Brisbane (capital) areas.
So, X R and X B were independent with sample size nR=38 and nB=42 with unknown
standard deviations.
Choice of test with justification
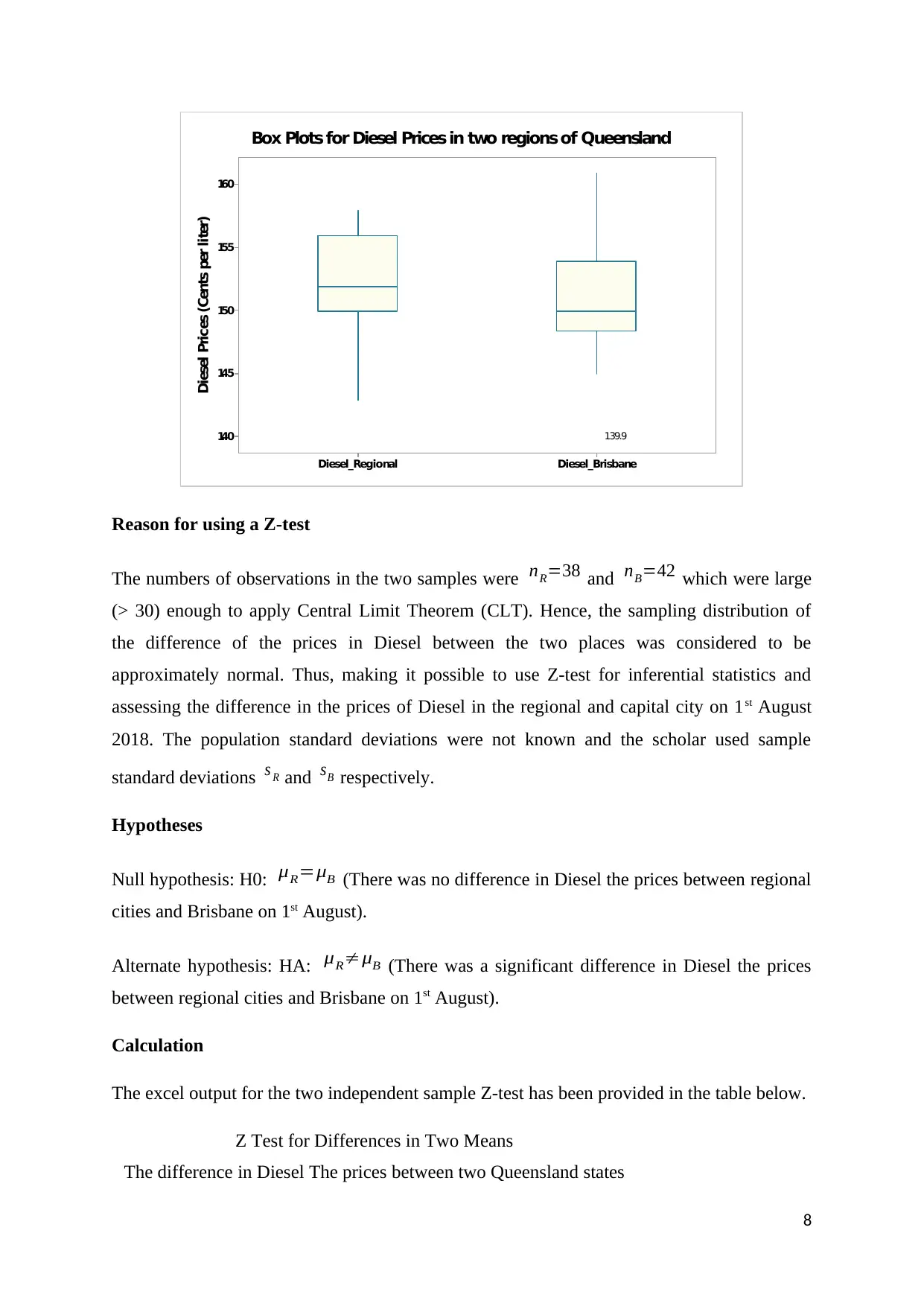
A side-by-side boxplot was used to indicate the distribution of Diesel the prices in regional
cities and capital city, Brisbane. Both the distributions were not normal and had small
positive skewness. This trend was in line with the histogram in Part A.
7
Appendix C1 – Statistical answer for Question 1
From the boxplots, it was also identified that there was some considerable number of petrol
pumps which sold Diesel for more than the median values, in both regional and capital city.
Hypothesis Test Difference Means Two Independent Samples
To answer Question 1 and to test whether there existed a difference in average the prices of
Diesel between regional cities and capital city Brisbane, the scholar used level of significance
of 5%.
Choice of technique
Technique: Hypothesis test for difference of two independent means
The petrol pumps in regional cities and the capital city were selected randomly. There were
no common petrol pumps in the two sub-samples. Therefore, the samples were considered to
be independent.
Random Variables
Let X R and X B denote the price of Diesel in regional and Brisbane (capital) areas.
Let μR and μB denote the average the price of Diesel in regional and Brisbane (capital) areas.
So, X R and X B were independent with sample size nR=38 and nB=42 with unknown
standard deviations.
Choice of test with justification
A side-by-side boxplot was used to indicate the distribution of Diesel the prices in regional
cities and capital city, Brisbane. Both the distributions were not normal and had small
positive skewness. This trend was in line with the histogram in Part A.
7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Diesel_BrisbaneDiesel_Regional
160
155
150
145
140
Diesel Prices (Cents per liter)
139.9
Box Plots for Diesel Prices in two regions of Queensland
Reason for using a Z-test
The numbers of observations in the two samples were nR=38 and nB=42 which were large
(> 30) enough to apply Central Limit Theorem (CLT). Hence, the sampling distribution of
the difference of the prices in Diesel between the two places was considered to be
approximately normal. Thus, making it possible to use Z-test for inferential statistics and
assessing the difference in the prices of Diesel in the regional and capital city on 1st August
2018. The population standard deviations were not known and the scholar used sample
standard deviations s R and sB respectively.
Hypotheses
Null hypothesis: H0: μR=μB (There was no difference in Diesel the prices between regional
cities and Brisbane on 1st August).
Alternate hypothesis: HA: μR≠μB (There was a significant difference in Diesel the prices
between regional cities and Brisbane on 1st August).
Calculation
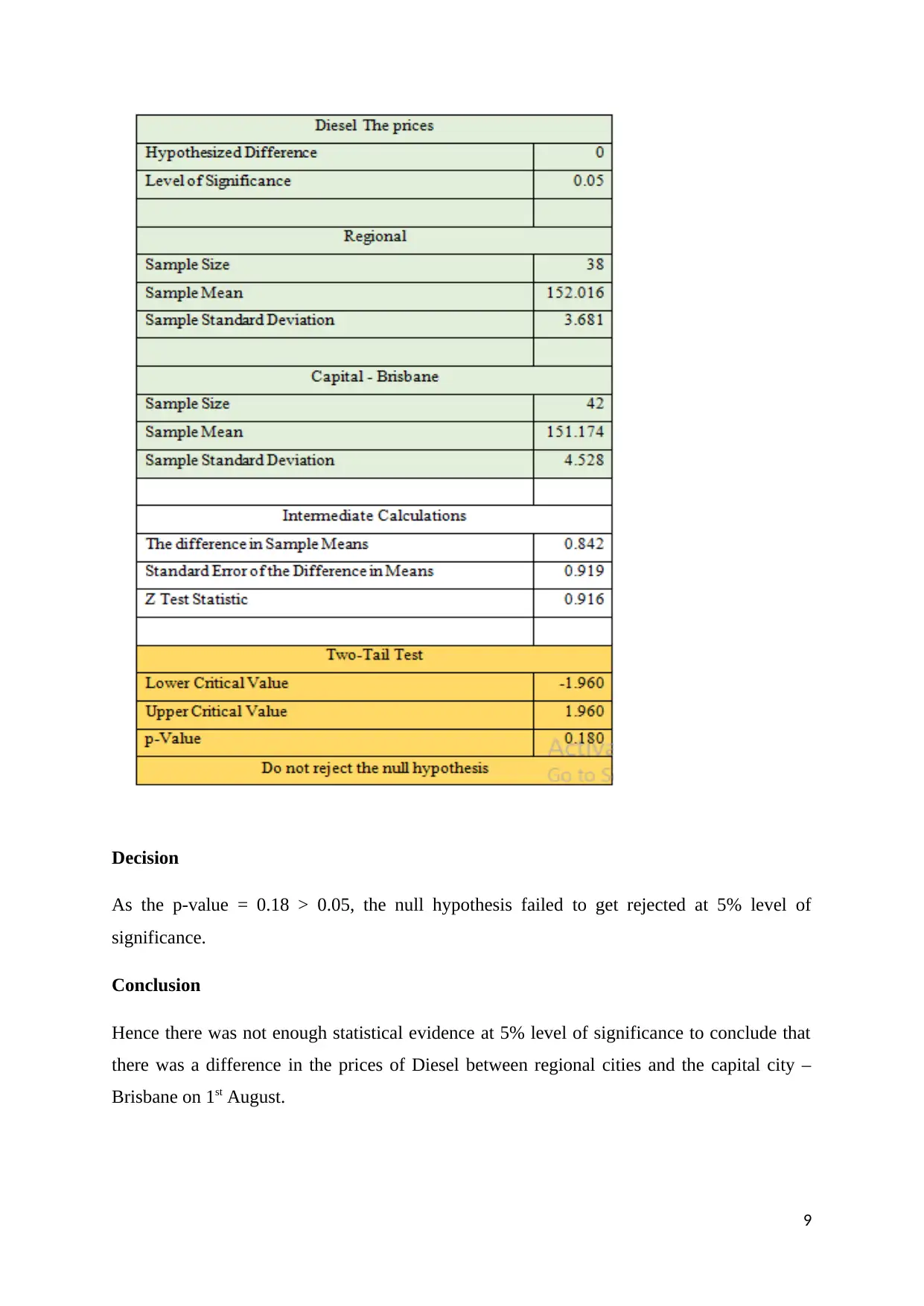
The excel output for the two independent sample Z-test has been provided in the table below.
Z Test for Differences in Two Means
The difference in Diesel The prices between two Queensland states
8
160
155
150
145
140
Diesel Prices (Cents per liter)
139.9
Box Plots for Diesel Prices in two regions of Queensland
Reason for using a Z-test
The numbers of observations in the two samples were nR=38 and nB=42 which were large
(> 30) enough to apply Central Limit Theorem (CLT). Hence, the sampling distribution of
the difference of the prices in Diesel between the two places was considered to be
approximately normal. Thus, making it possible to use Z-test for inferential statistics and
assessing the difference in the prices of Diesel in the regional and capital city on 1st August
2018. The population standard deviations were not known and the scholar used sample
standard deviations s R and sB respectively.
Hypotheses
Null hypothesis: H0: μR=μB (There was no difference in Diesel the prices between regional
cities and Brisbane on 1st August).
Alternate hypothesis: HA: μR≠μB (There was a significant difference in Diesel the prices
between regional cities and Brisbane on 1st August).
Calculation
The excel output for the two independent sample Z-test has been provided in the table below.
Z Test for Differences in Two Means
The difference in Diesel The prices between two Queensland states
8
Decision
As the p-value = 0.18 > 0.05, the null hypothesis failed to get rejected at 5% level of
significance.
Conclusion
Hence there was not enough statistical evidence at 5% level of significance to conclude that
there was a difference in the prices of Diesel between regional cities and the capital city –
Brisbane on 1st August.
9
As the p-value = 0.18 > 0.05, the null hypothesis failed to get rejected at 5% level of
significance.
Conclusion
Hence there was not enough statistical evidence at 5% level of significance to conclude that
there was a difference in the prices of Diesel between regional cities and the capital city –
Brisbane on 1st August.
9
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Appendix C.2 – Statistical answer for Question 2
Simple Linear Regression Model
The scholar used a simple regression model to estimate the price of Unleaded 91 in the price
of Diesel in Queensland, Australia.
Assumptions and Variables
The assumption of independence between the prices of Unleaded 91 in the prices of Diesel in
Queensland for the linear regression was presumed. Considering the scatter diagram, the
linearity relation between the predictor and the estimated variables was also anticipated. The
price of Unleaded 91 was dependent and the price of Diesel in Queensland was the
independent variables. The dependent variable was also considered to be normally
distributed.
Let Xun = the price of Unleaded 91 (Dependent Variable)
Xdl = The price of Diesel (Independent Variable)
Simple Linear Regression Model
The price of Unleaded 91: Dependent Variable
The price of Diesel: Independent Variable
10
Simple Linear Regression Model
The scholar used a simple regression model to estimate the price of Unleaded 91 in the price
of Diesel in Queensland, Australia.
Assumptions and Variables
The assumption of independence between the prices of Unleaded 91 in the prices of Diesel in
Queensland for the linear regression was presumed. Considering the scatter diagram, the
linearity relation between the predictor and the estimated variables was also anticipated. The
price of Unleaded 91 was dependent and the price of Diesel in Queensland was the
independent variables. The dependent variable was also considered to be normally
distributed.
Let Xun = the price of Unleaded 91 (Dependent Variable)
Xdl = The price of Diesel (Independent Variable)
Simple Linear Regression Model
The price of Unleaded 91: Dependent Variable
The price of Diesel: Independent Variable
10
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

The Scatterplot revealed a moderately strong linear relationship between the prices of
Unleaded 91 and Diesel, in Queensland.
Equation and Coefficients
Regression equation and coefficients
The price of Unleaded 91 = 0.82 * The price of Diesel + 18.06
Correlation coefficients
r = 0.513, r2
= 0.263
Interpretation of Regression Coefficients
The gradient of regression was b1 = 0.82, which indicated that for an increase in Diesel the
prices by 1 cent would also increase the price of Unleaded by 0.82 cents.
The vertical intercept was b0 = 18.06, which indicated that the price of Unleaded 91 fuel will
be 18.06 cents, even if the price of Diesel becomes zero.
11
Unleaded 91 and Diesel, in Queensland.
Equation and Coefficients
Regression equation and coefficients
The price of Unleaded 91 = 0.82 * The price of Diesel + 18.06
Correlation coefficients
r = 0.513, r2
= 0.263
Interpretation of Regression Coefficients
The gradient of regression was b1 = 0.82, which indicated that for an increase in Diesel the
prices by 1 cent would also increase the price of Unleaded by 0.82 cents.
The vertical intercept was b0 = 18.06, which indicated that the price of Unleaded 91 fuel will
be 18.06 cents, even if the price of Diesel becomes zero.
11

Interpretation of Correlation Coefficients
Correlation coefficient = 0.513, which indicated a moderately strong linear relation between
the prices of Diesel and Unleaded 91. This trend was in line with the scatter plot with the
price of Unleaded 91 as the dependent variable.
The coefficient of determination was evaluated as r2
= 0.263, indicating that approximately
26.3% variation in the prices of Unleaded 91 was explained by variation in the prices of
Diesel in Queensland.
12
Correlation coefficient = 0.513, which indicated a moderately strong linear relation between
the prices of Diesel and Unleaded 91. This trend was in line with the scatter plot with the
price of Unleaded 91 as the dependent variable.
The coefficient of determination was evaluated as r2
= 0.263, indicating that approximately
26.3% variation in the prices of Unleaded 91 was explained by variation in the prices of
Diesel in Queensland.
12
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
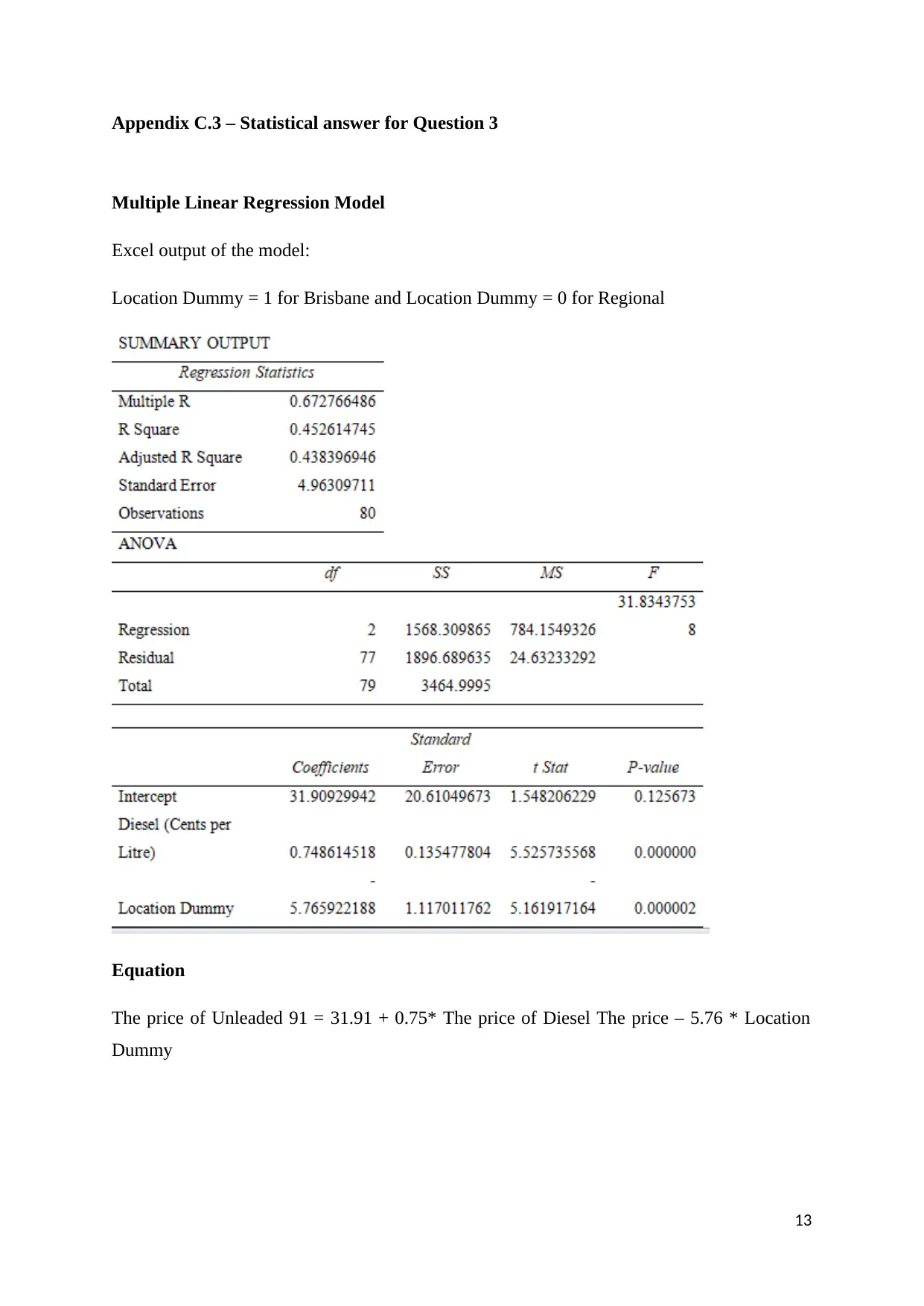
Appendix C.3 – Statistical answer for Question 3
Multiple Linear Regression Model
Excel output of the model:
Location Dummy = 1 for Brisbane and Location Dummy = 0 for Regional
Equation
The price of Unleaded 91 = 31.91 + 0.75* The price of Diesel The price – 5.76 * Location
Dummy
13
Multiple Linear Regression Model
Excel output of the model:
Location Dummy = 1 for Brisbane and Location Dummy = 0 for Regional
Equation
The price of Unleaded 91 = 31.91 + 0.75* The price of Diesel The price – 5.76 * Location
Dummy
13
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Interpretation of Regression Coefficients
The gradient of Diesel the price: b1 = 0.749, which indicated that for an increase in Diesel
the prices by 1 cent, the price of Unleaded 91 fuel would increase approximately by 0.749
cents.
The gradient of location dummy b2 = -5.766, which indicated that Unleaded 91 fuel was less
costly by 5.766 cents in Brisbane compared to regional area petrol pumps.
The vertical intercept was b0 = 31.91, indicating that the price of Unleaded 91 fuel was 31.91
cents when the price of Diesel was zero in Regional areas of Queensland (location = 0).
Interpretation of Correlation Coefficients
Multiple correlation coefficient: r = 0.673, which indicated a moderately high linear
relationship between the price of Unleaded 91 fuel, the price of Diesel and location of a
petrol pump.
The coefficient of Determination: r2
= 0.453, indicating that variation in the prices of
Unleaded 91 was explained in 45.3% cases by variation of Diesel the price and location of
the petrol pump.
Comparison of the models
The multiple correlation coefficient was r = 0.673, whereas the correlation coefficient for the
simple regression model was r = 0.513. Hence, including a location in the model increased
the linear relationship between the variables.
The coefficient of determination was r2
= 0.453, whereas for simple regression model the
coefficient of determination was r2
= 0.263. Hence, including location as a variable increased
the predictability of the model by approximately 19%.
Therefore, adding a location in the regression model as an independent variable resulted in a
stronger estimation model that was able to explain more variation in the price of Unleaded 91
fuel.
14
The gradient of Diesel the price: b1 = 0.749, which indicated that for an increase in Diesel
the prices by 1 cent, the price of Unleaded 91 fuel would increase approximately by 0.749
cents.
The gradient of location dummy b2 = -5.766, which indicated that Unleaded 91 fuel was less
costly by 5.766 cents in Brisbane compared to regional area petrol pumps.
The vertical intercept was b0 = 31.91, indicating that the price of Unleaded 91 fuel was 31.91
cents when the price of Diesel was zero in Regional areas of Queensland (location = 0).
Interpretation of Correlation Coefficients
Multiple correlation coefficient: r = 0.673, which indicated a moderately high linear
relationship between the price of Unleaded 91 fuel, the price of Diesel and location of a
petrol pump.
The coefficient of Determination: r2
= 0.453, indicating that variation in the prices of
Unleaded 91 was explained in 45.3% cases by variation of Diesel the price and location of
the petrol pump.
Comparison of the models
The multiple correlation coefficient was r = 0.673, whereas the correlation coefficient for the
simple regression model was r = 0.513. Hence, including a location in the model increased
the linear relationship between the variables.
The coefficient of determination was r2
= 0.453, whereas for simple regression model the
coefficient of determination was r2
= 0.263. Hence, including location as a variable increased
the predictability of the model by approximately 19%.
Therefore, adding a location in the regression model as an independent variable resulted in a
stronger estimation model that was able to explain more variation in the price of Unleaded 91
fuel.
14

Statistical Inference
Assumptions and variables defined
Choice of technique
Technique: Hypothesis testing to test the significance of linearity of the independent
variables
Hypotheses
For Diesel: H0: βDiesel=0 (Diesel the price not significant) against H0A: βDiesel≠0 (Diesel
the price significant)
For location H1: βlocation=0 (Location not significant) against H1A: βlocation≠0 (Location
significant)
Level of significance used = 5%
Decision
Decisions were based on the p-values of the regression model at 5% level of significance.
i. P-value for Diesel the price = 0.000000 < 0.05: The null hypothesis H0 rejected and
H0A accepted.
ii. P-value for location = 0.000002 < 0.05: The null hypothesis H1 rejected and H1A
accepted.
The above decisions were also valid for 1% level of significance.
Preferred Regression Model
At 5% level of significance or even at 1% level of significance, Multiple Regression Model
with both Diesel the price and location of petrol pumps was the best choice to estimate the
price of Unleaded 91 fuel in Queensland, Australia.
15
Assumptions and variables defined
Choice of technique
Technique: Hypothesis testing to test the significance of linearity of the independent
variables
Hypotheses
For Diesel: H0: βDiesel=0 (Diesel the price not significant) against H0A: βDiesel≠0 (Diesel
the price significant)
For location H1: βlocation=0 (Location not significant) against H1A: βlocation≠0 (Location
significant)
Level of significance used = 5%
Decision
Decisions were based on the p-values of the regression model at 5% level of significance.
i. P-value for Diesel the price = 0.000000 < 0.05: The null hypothesis H0 rejected and
H0A accepted.
ii. P-value for location = 0.000002 < 0.05: The null hypothesis H1 rejected and H1A
accepted.
The above decisions were also valid for 1% level of significance.
Preferred Regression Model
At 5% level of significance or even at 1% level of significance, Multiple Regression Model
with both Diesel the price and location of petrol pumps was the best choice to estimate the
price of Unleaded 91 fuel in Queensland, Australia.
15
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 15
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.




