Statistical Problems and Analysis in Descriptive Statistics, Sampling, Regression and Hypothesis Testing

This article discusses statistical problems and analysis in descriptive statistics, sampling, regression and hypothesis testing. It includes tables, figures, and formulas to explain the concepts. The article also provides references for further reading.

Statistical Problems
Student Name: Student ID:
Unit Name: Unit ID:
Date Due: Professor Name:
1

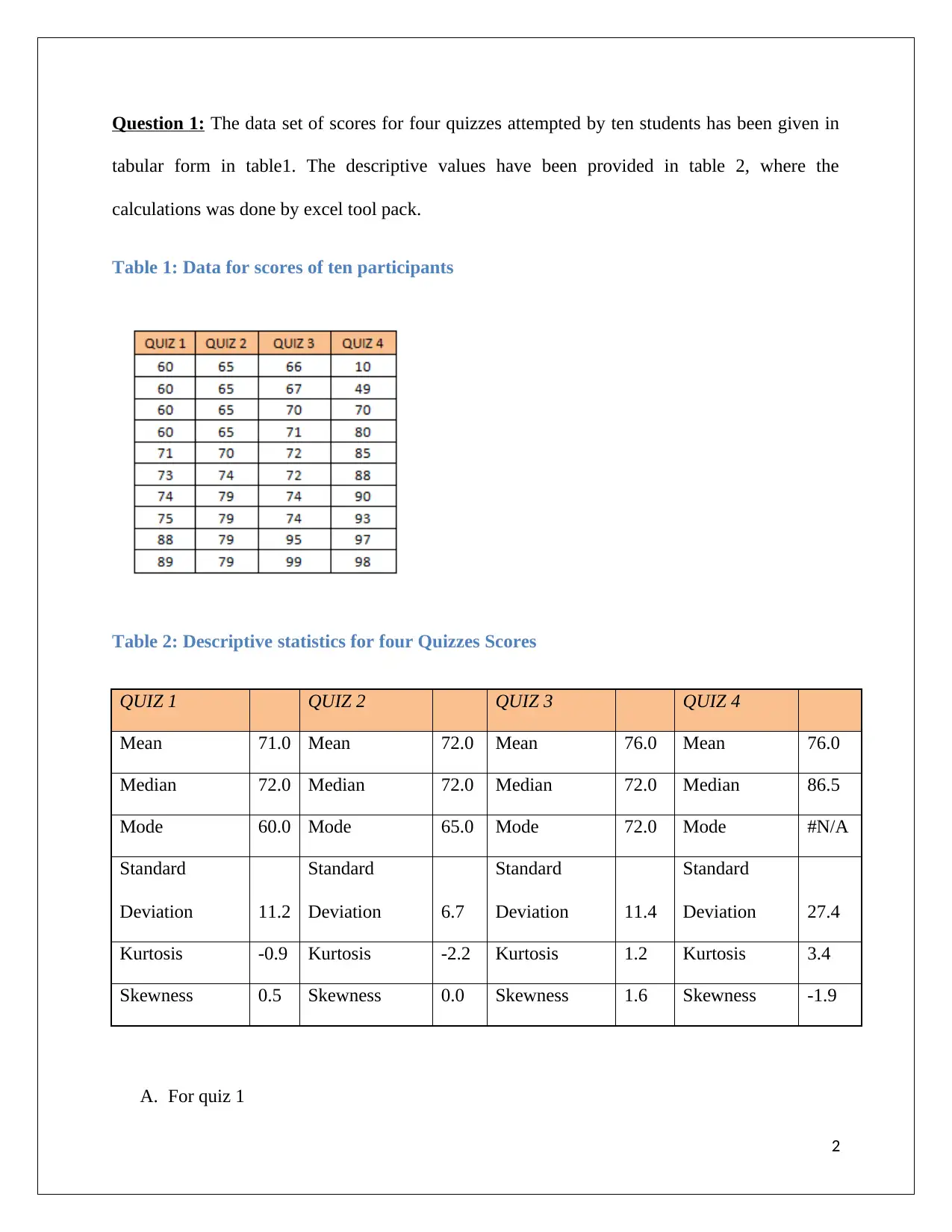
Question 1: The data set of scores for four quizzes attempted by ten students has been given in
tabular form in table1. The descriptive values have been provided in table 2, where the
calculations was done by excel tool pack.
Table 1: Data for scores of ten participants
Table 2: Descriptive statistics for four Quizzes Scores
QUIZ 1 QUIZ 2 QUIZ 3 QUIZ 4
Mean 71.0 Mean 72.0 Mean 76.0 Mean 76.0
Median 72.0 Median 72.0 Median 72.0 Median 86.5
Mode 60.0 Mode 65.0 Mode 72.0 Mode #N/A
Standard
Deviation 11.2
Standard
Deviation 6.7
Standard
Deviation 11.4
Standard
Deviation 27.4
Kurtosis -0.9 Kurtosis -2.2 Kurtosis 1.2 Kurtosis 3.4
Skewness 0.5 Skewness 0.0 Skewness 1.6 Skewness -1.9
A. For quiz 1
2

Mean =
∑ Quiz 1 scores
frequency =710
10 =71 . 0
Median =
10+1
2 =5 . 5 th observation. So Median =
1
2∗ ( 71+73 ) =72. 0
Mode = Data with highest frequency = 60.0
For Quiz 2
Mean =
∑ Quiz 2 scores
frequency =720
10 =72 . 0
Median =
10+1
2 =5 . 5 th observation. So Median =
1
2∗ ( 70+ 74 ) =72. 0
Mode = Data with highest frequency = 65.0
For Quiz 3
Mean =
∑ Quiz 3 scores
frequency =760
10 =76 .0
Median =
10+1
2 =5 . 5 th observation. So Median =
1
2∗ ( 72+72 ) =72. 0
Mode = Data with highest frequency = 72.0
For Quiz 3
Mean =
∑ Quiz 4 scores
frequency =760
10 =76 . 0
3

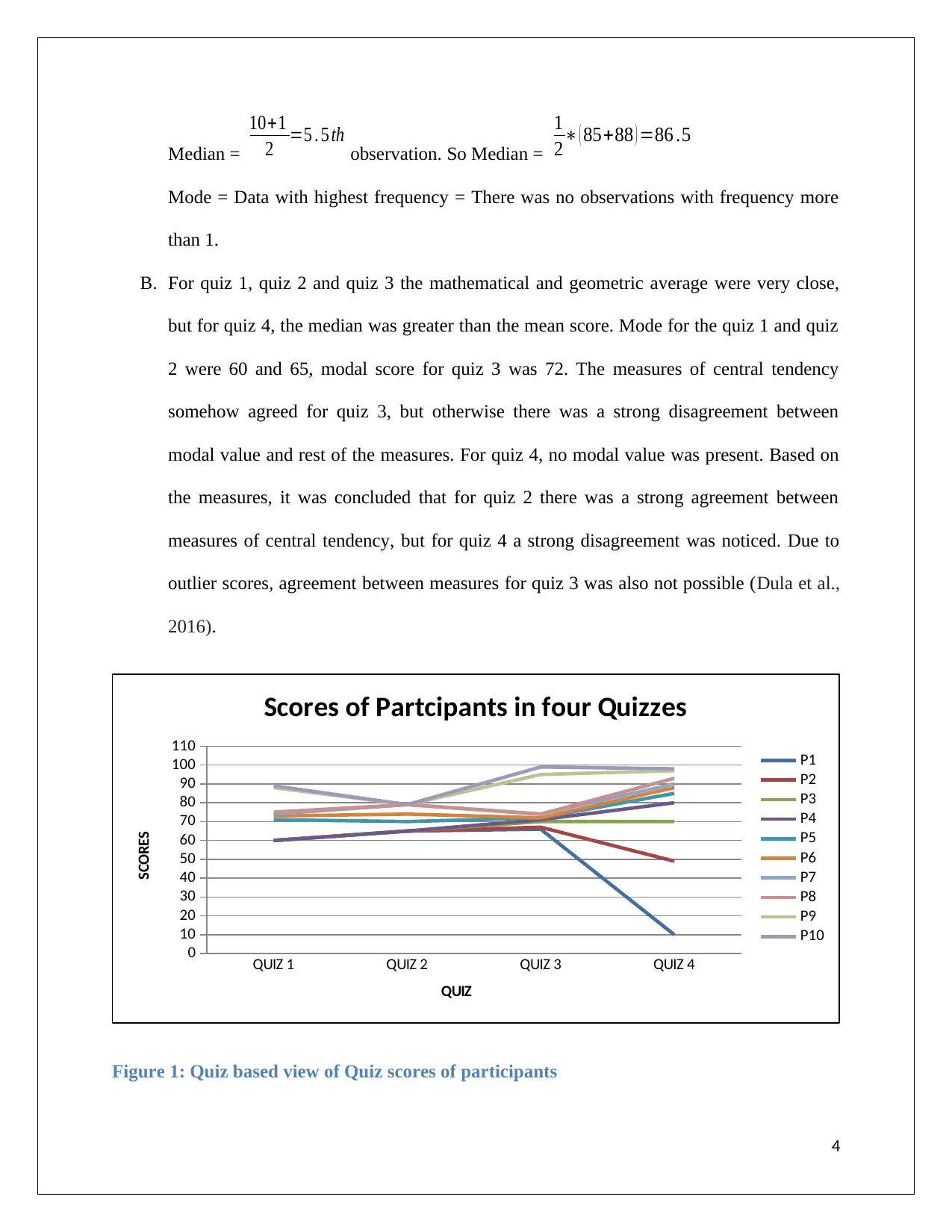
Median =
10+1
2 =5 . 5 th observation. So Median =
1
2∗ ( 85+88 ) =86 .5
Mode = Data with highest frequency = There was no observations with frequency more
than 1.
B. For quiz 1, quiz 2 and quiz 3 the mathematical and geometric average were very close,
but for quiz 4, the median was greater than the mean score. Mode for the quiz 1 and quiz
2 were 60 and 65, modal score for quiz 3 was 72. The measures of central tendency
somehow agreed for quiz 3, but otherwise there was a strong disagreement between
modal value and rest of the measures. For quiz 4, no modal value was present. Based on
the measures, it was concluded that for quiz 2 there was a strong agreement between
measures of central tendency, but for quiz 4 a strong disagreement was noticed. Due to
outlier scores, agreement between measures for quiz 3 was also not possible (Dula et al.,
2016).
QUIZ 1 QUIZ 2 QUIZ 3 QUIZ 4
0
10
20
30
40
50
60
70
80
90
100
110
Scores of Partcipants in four Quizzes
P1
P2
P3
P4
P5
P6
P7
P8
P9
P10
QUIZ
SCORES
Figure 1: Quiz based view of Quiz scores of participants
4

1 2 3 4 5 6 7 8 9 10
0
20
40
60
80
100
120
Comparison of Quiz Scores
QUIZ 1
QUIZ 2
QUIZ 3
QUIZ 4
PARTICIPANTS
SCORES
Figure 2: Participant view of Quiz scores
C. For quiz 1, the measure statistics were almost equal other than the mode. The modal value
was very deceptive in quiz 1 score. It was easy to get carried away by the highest frequency
measure, but in reality it was a weak estimate of the data. Quiz 2 scores were the most
accumulated scores compared to other three quizzes. All the three measures agreed in this case.
For the third quiz, due to few outlier values, the mean value was affected. Hence, for quiz 3,
mean was not an exact measure of central tendency. Quiz 4 was the most interesting one with
high variability due to scattered data. Outliers affected the mean, and its value was far less than
the geometrical measure. Mead and mode, both were inappropriate for this case.
5

Figure 3: Normality of quiz 1
Figure 4: Quiz2 normality check
6

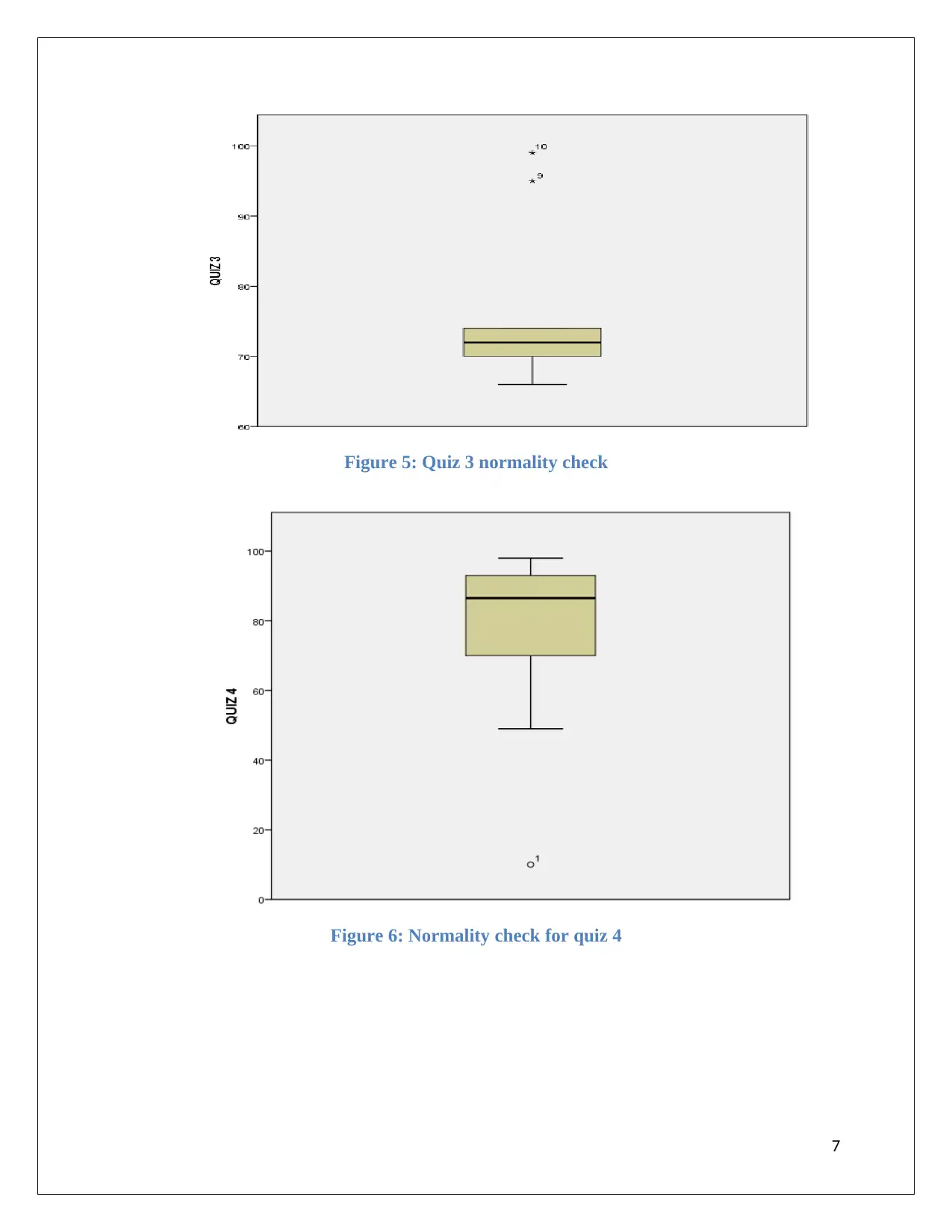
Figure 5: Quiz 3 normality check
Figure 6: Normality check for quiz 4
7

D. The data were skewed in nature. For quiz 1 and quiz 3 the distributions were positively
skewed, whereas for the last quiz data distributions, skewness was high negative. Quiz 4
data were highly skewed with kurtosis of 3.4. The distribution was leptokurtic in nature
for quiz 3, whereas platykurtic for quiz 1 and 2.
E. From figure 1 the performance of ten participants in four quizzes was clear. Figure 2 was
more appropriate in graphical representation of scores of each participant. Participant 1
performed very poorly in quiz four, but was consistent in other three quizzes.
Performance of the third participant was consistent throughout all the quizzes.
Participants 4 to 8 performed consistently well in quiz 4, whereas scores for participant 9
and 10 for quiz 4 and quiz 3 were better than other two quizzes. Consistent and average
performance was noticed for quiz 2 and 3 for all of the candidates (Mertler & Reinhart,
2016).
Question 2:
A. Here proportion for almonds, p
^¿
¿ was 19/100=0.19. hence the confidence interval was
calculated using the formula, p
^¿ ± z∗ √ p
^¿ ¿¿
¿¿ ¿¿
¿ where n is the sample size. So, for 90%
confidence interval, z=1 .645 and the confidence interval was
019±1 . 645∗ √ 0 .19∗0 . 81
100 =0 .19±1. 645∗0 .04=[0 . 124 . 0 .260 ]
8

B. As the sample size was 100 (greater than 30), normality of the data can be assumed,
based on the assistance of central limit theorem. For sample size greater than 30, any
sampling distribution under limitations condition can approach towards a normal
distribution.
C. Error is calculated as ±z∗√ p
^¿ ¿¿
¿ ¿ ¿ ¿ . If ±z∗√ p
^¿ ¿¿
¿ ¿ ¿ ¿ then the following
calculations can be done,
±z∗√ p
^¿ ¿¿
¿ ¿ ¿ ¿
√ 0 . 19∗0 . 81
n = 0 . 03
1. 645 =0 . 18=> 0. 154
0 .18∗0 .18 =n=> n=4 . 75≃5 . Hence sample of 5 will
be sufficient to obtain such errors.
D. Quality control manager’s job is to smoothly run the manufacturing process within the
control limits of the process. Without knowledge of sampling, choice of sample size,
technique of sample selection, assessment of sample proportion will not be possible.
Without assessing the descriptive, confidence interval construction will be impossible.
Then it will be difficult to construct control limits for the process. Hence knowledge of
sampling is a must for quality control manager at Planter’s (Konieczka & Namiesnik,
2016).
Question 3
9

A. As the p-value was greater than 0.05, coefficient of price was insignificant in the
regression model, and at α = 0.05, the coefficient was not significantly different from
zero (Breiman, 2017).
B. R-square is the coefficient of determination, it signified that the independent factor
(price) of the model was able to define or explain merely 1% variation of the dependent
variable (sound quality) (Mitra, 2016).
C. Coefficient of price in regression model was negative, but the value was statistically
insignificant. Hence sound quality and price were almost independent of each other. So
higher price did not guarantee higher sound quality (Chatterjee & Hadi, 2015).
Question 4
A. Let μ denotes the average number of days for package delivery. Then the hypotheses are
as follows,
Null hypothesis: H0: ( μ=2 ) and alternate hypothesis was HA: ( μ>2 )
B. Wrongly accepting the null hypothesis when it is wrong is type II error. Hence, wrongly
accepting company’s claim about delivery timing will generate type II error.
C. Rejecting a true null hypothesis creates type I error. Hence, wrongly establishing
company’s delivery timing as more than two days will generate type I error.
D. From the company’s point of view, type I error is more dangerous. As type I error will
destroy company’s goodwill, increase total cost and will cause overall adverse effect on
the balance sheet, company will take type I error more seriously than type II error.
E. From customer point of view timely delivery is more important than reputation of the
company. Type II error will misguide the customers about the exact delivery time of the
10

packages, and hence will create a state of confusion and disbelief. Hence from customer
point of view, type II error is more heinous (Hopkins, 2017).
References
Breiman, L., 2017. Classification and regression trees. Routledge.
Chatterjee, S. and Hadi, A.S., 2015. Regression analysis by example. John Wiley & Sons.
Dula, M., Mogusu, E., Strasser, S., Liu, Y. and Zheng, S., 2016. Median and Mode
Approximation for Skewed Unimodal Continuous Distributions using Taylor Series Expansion.
Hopkins, W.G., 2017. A Spreadsheet for Deriving a Confidence Interval, Mechanistic Inference
and Clinical Inference from a P Value. Sportscience, 21.
Konieczka, P. and Namiesnik, J., 2016. Quality assurance and quality control in the analytical
chemical laboratory: a practical approach. CRC Press.
Mertler, C.A. and Reinhart, R.V., 2016. Advanced and multivariate statistical methods:
Practical application and interpretation. Taylor & Francis.
Mitra, A., 2016. Fundamentals of quality control and improvement. John Wiley & Sons.
11