BSCS 11053 Statistics Assignment: Data Analysis and Interpretation
VerifiedAdded on 2023/06/11
|10
|1653
|58
Homework Assignment
AI Summary
This statistics assignment solution covers various aspects of data analysis and interpretation. It includes analyzing pie charts, bar charts, and frequency tables, assessing whether graphs are clearly labeled and adhere to the area principle, and interpreting data from articles. The solution also involves describing data distributions, identifying potential factors influencing data shape, and discussing the appropriateness of statistical measures like mean and standard deviation for skewed data. Furthermore, it explores the relationship between physical activity and BMI using graphical displays and addresses the limitations of inferring causation. The assignment also includes constructing and interpreting histograms, boxplots, and stem-and-leaf displays, along with identifying outliers and choosing appropriate summary statistics for skewed distributions. Finally, it involves applying the empirical rule to a normal distribution to determine probabilities and intervals for battery life, providing a comprehensive overview of statistical concepts and their practical applications. Desklib provides similar solved assignments and past papers.

Statistics
Name:
Institution:
30th May 2018
Name:
Institution:
30th May 2018
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
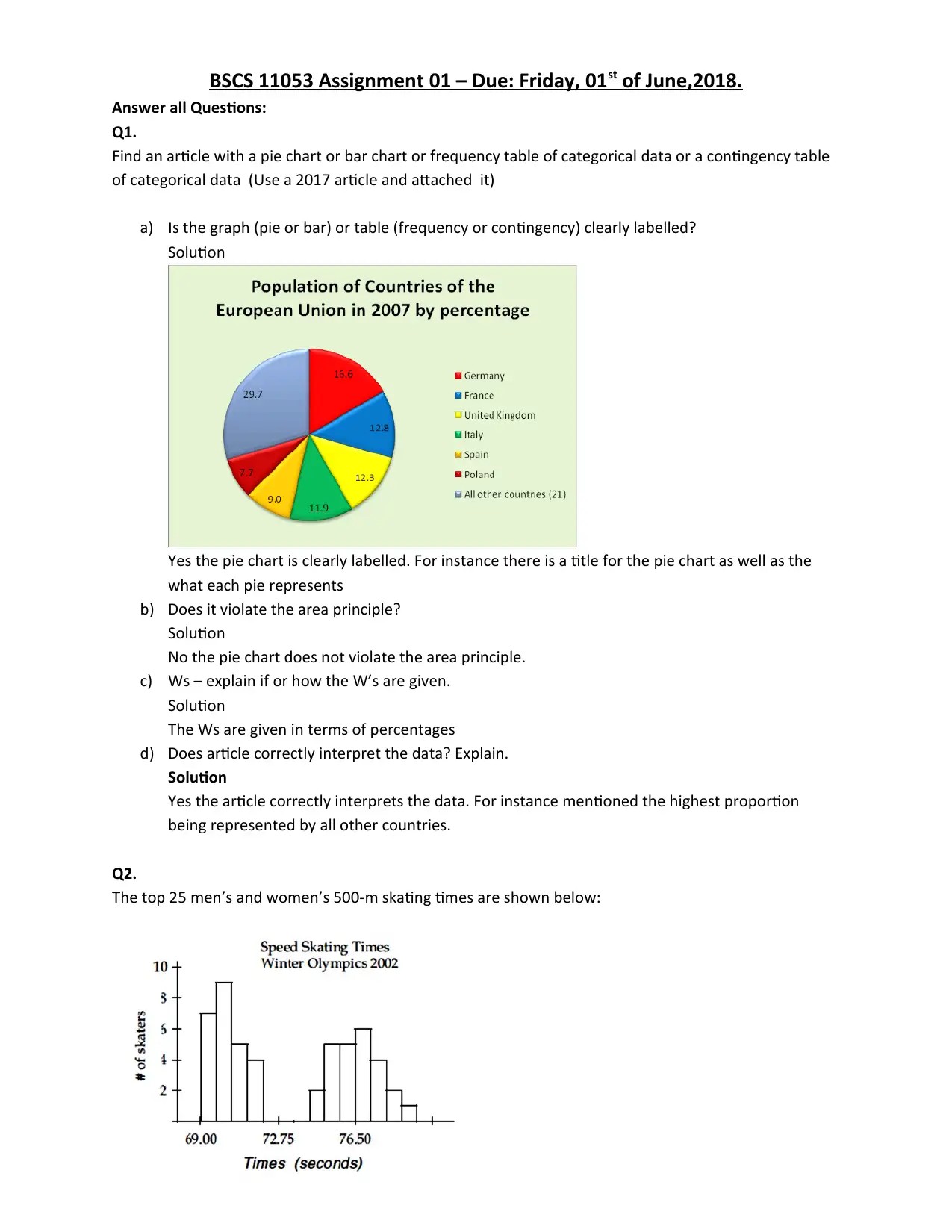
BSCS 11053 Assignment 01 – Due: Friday, 01st of June,2018.
Answer all Questions:
Q1.
Find an article with a pie chart or bar chart or frequency table of categorical data or a contingency table
of categorical data (Use a 2017 article and attached it)
a) Is the graph (pie or bar) or table (frequency or contingency) clearly labelled?
Solution
Yes the pie chart is clearly labelled. For instance there is a title for the pie chart as well as the
what each pie represents
b) Does it violate the area principle?
Solution
No the pie chart does not violate the area principle.
c) Ws – explain if or how the W’s are given.
Solution
The Ws are given in terms of percentages
d) Does article correctly interpret the data? Explain.
Solution
Yes the article correctly interprets the data. For instance mentioned the highest proportion
being represented by all other countries.
Q2.
The top 25 men’s and women’s 500-m skating times are shown below:
Answer all Questions:
Q1.
Find an article with a pie chart or bar chart or frequency table of categorical data or a contingency table
of categorical data (Use a 2017 article and attached it)
a) Is the graph (pie or bar) or table (frequency or contingency) clearly labelled?
Solution
Yes the pie chart is clearly labelled. For instance there is a title for the pie chart as well as the
what each pie represents
b) Does it violate the area principle?
Solution
No the pie chart does not violate the area principle.
c) Ws – explain if or how the W’s are given.
Solution
The Ws are given in terms of percentages
d) Does article correctly interpret the data? Explain.
Solution
Yes the article correctly interprets the data. For instance mentioned the highest proportion
being represented by all other countries.
Q2.
The top 25 men’s and women’s 500-m skating times are shown below:

a) What type of graph has been constructed for these skating times?
Solution
This is a histogram
b) Describe the distribution.
Solution
The distribution is seems to be skewed to the right (i.e. longer tail to the right).
c) What do you think might account for this shape?
Solution
Variation in the speed during different times for instance presence of snow might reduce the
skating speed. So the speed when there is snow and when there is no snow would vary greatly
bringing about the outliers in the data.
d) A statistics student used this skating data to find a mean of 73.46 seconds with a standard
deviation of 3.33 seconds. Why are these measures of center and spread not particularly
meaningful for these data? Explain.
Solution
Because the data is skewed and in a skewed data mean or standard deviation does not have a
meaningful interpretation.
Q3.
Obesity and exercise. The centers for Disease Control and Prevention (CDC) has estimated that 19.8% of
Americans over 15 years old are obese. The CDC conducts a survey on obesity and various behaviors.
Here is a table on self-reported exercise classified by body mass index (BMI):
Body Mass Index
Physical Activity Normal
%
Overweight
%
Obese
%
Inactive 23.8 26.0 35.6
Irregularly active 27.8 28.7 28.1
Regular, not intense 31.6 31.1 27.2
Regular, intense 16.8 14.2 9.1
a) Are these percentages column percentages, row percentages, or table percentages?
Solution
The percentages are given as column percentages
b) Use graphical displays to show different percentages of physical activities for the three BMI
groups (Use SPSS).
Solution
Solution
This is a histogram
b) Describe the distribution.
Solution
The distribution is seems to be skewed to the right (i.e. longer tail to the right).
c) What do you think might account for this shape?
Solution
Variation in the speed during different times for instance presence of snow might reduce the
skating speed. So the speed when there is snow and when there is no snow would vary greatly
bringing about the outliers in the data.
d) A statistics student used this skating data to find a mean of 73.46 seconds with a standard
deviation of 3.33 seconds. Why are these measures of center and spread not particularly
meaningful for these data? Explain.
Solution
Because the data is skewed and in a skewed data mean or standard deviation does not have a
meaningful interpretation.
Q3.
Obesity and exercise. The centers for Disease Control and Prevention (CDC) has estimated that 19.8% of
Americans over 15 years old are obese. The CDC conducts a survey on obesity and various behaviors.
Here is a table on self-reported exercise classified by body mass index (BMI):
Body Mass Index
Physical Activity Normal
%
Overweight
%
Obese
%
Inactive 23.8 26.0 35.6
Irregularly active 27.8 28.7 28.1
Regular, not intense 31.6 31.1 27.2
Regular, intense 16.8 14.2 9.1
a) Are these percentages column percentages, row percentages, or table percentages?
Solution
The percentages are given as column percentages
b) Use graphical displays to show different percentages of physical activities for the three BMI
groups (Use SPSS).
Solution
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
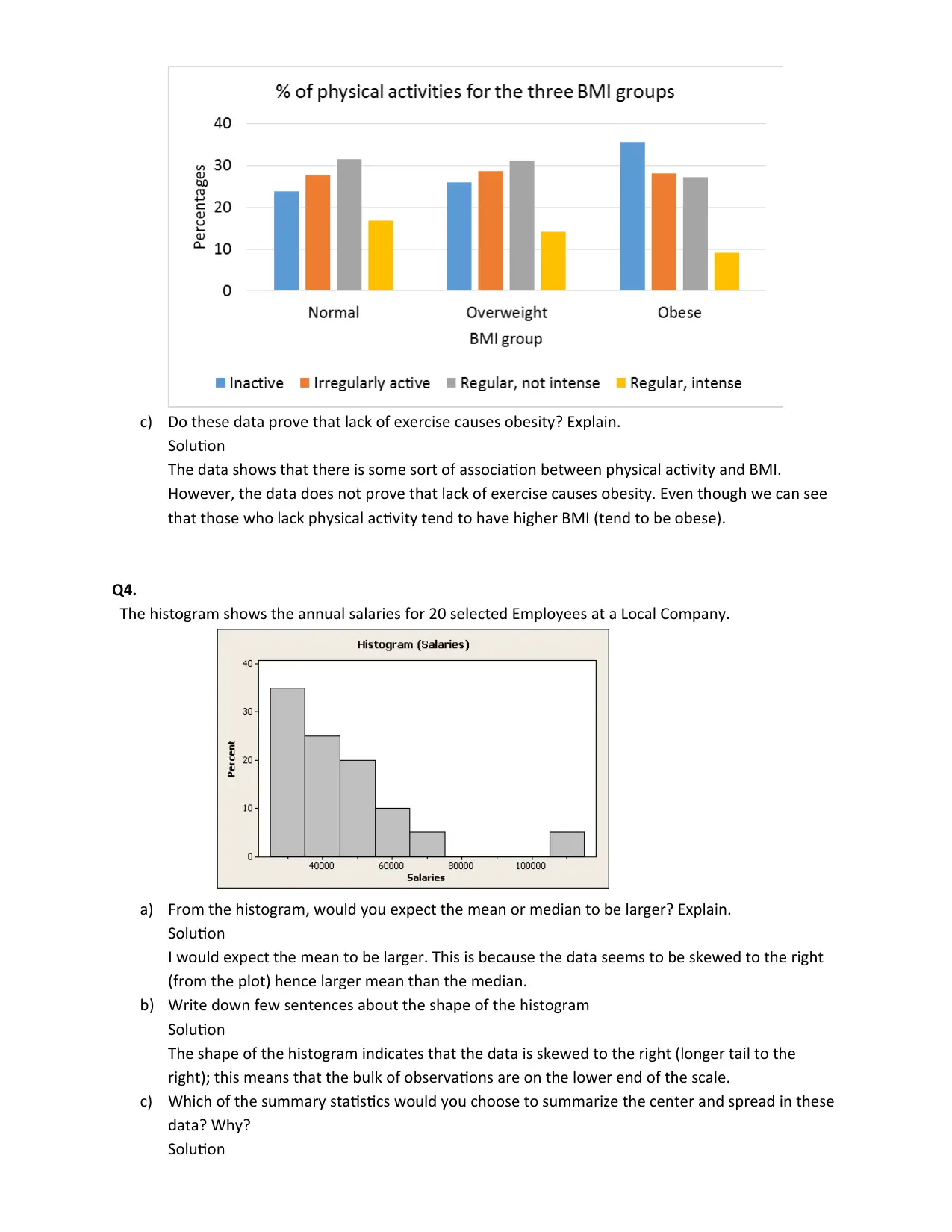
c) Do these data prove that lack of exercise causes obesity? Explain.
Solution
The data shows that there is some sort of association between physical activity and BMI.
However, the data does not prove that lack of exercise causes obesity. Even though we can see
that those who lack physical activity tend to have higher BMI (tend to be obese).
Q4.
The histogram shows the annual salaries for 20 selected Employees at a Local Company.
a) From the histogram, would you expect the mean or median to be larger? Explain.
Solution
I would expect the mean to be larger. This is because the data seems to be skewed to the right
(from the plot) hence larger mean than the median.
b) Write down few sentences about the shape of the histogram
Solution
The shape of the histogram indicates that the data is skewed to the right (longer tail to the
right); this means that the bulk of observations are on the lower end of the scale.
c) Which of the summary statistics would you choose to summarize the center and spread in these
data? Why?
Solution
Solution
The data shows that there is some sort of association between physical activity and BMI.
However, the data does not prove that lack of exercise causes obesity. Even though we can see
that those who lack physical activity tend to have higher BMI (tend to be obese).
Q4.
The histogram shows the annual salaries for 20 selected Employees at a Local Company.
a) From the histogram, would you expect the mean or median to be larger? Explain.
Solution
I would expect the mean to be larger. This is because the data seems to be skewed to the right
(from the plot) hence larger mean than the median.
b) Write down few sentences about the shape of the histogram
Solution
The shape of the histogram indicates that the data is skewed to the right (longer tail to the
right); this means that the bulk of observations are on the lower end of the scale.
c) Which of the summary statistics would you choose to summarize the center and spread in these
data? Why?
Solution
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Median would be ideal to summarize the center while for the spread Quartiles would be ideal.
The two have be chosen since they are less affected by outliers or by a skewed dataset like the
one above.
Q5.
The following data give the number of workers (in thousand) employed by a small companies in all 50
states of USA.
786 128 930 476 6800 981 759 171 2900 1500
253 259 2600 1300 642 588 734 853 292 1100
1500 2000 1200 452 1200 210 383 402 302 1800
319 3800 1600 161 2300 645 736 2500 238 739
189 1000 3800 430 162 1400 1200 303 1300 123
For the above data, answer the following questions by hand or using SPSS. Include your calculations or
the SPSS output.
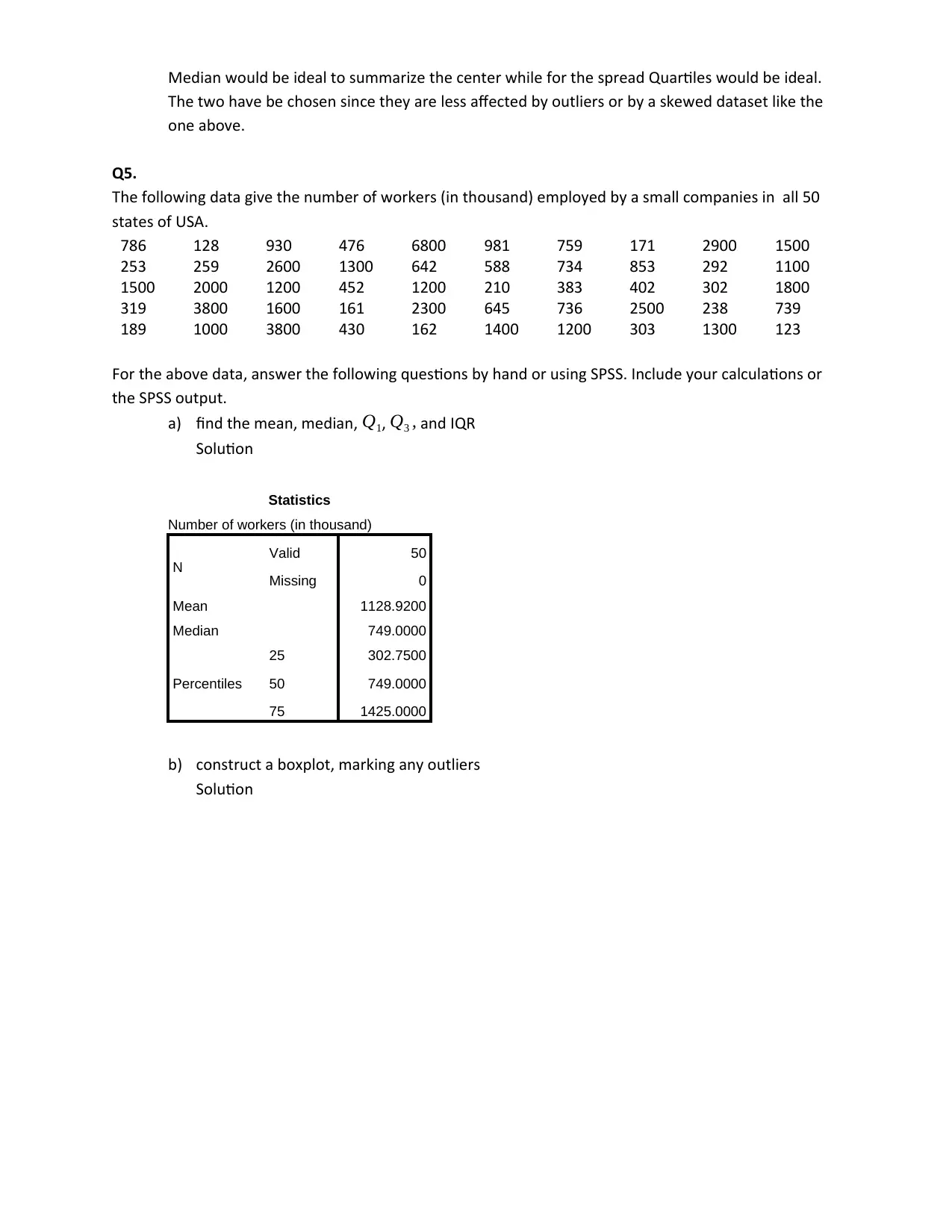
a) find the mean, median, Q1, Q3 , and IQR
Solution
Statistics
Number of workers (in thousand)
N Valid 50
Missing 0
Mean 1128.9200
Median 749.0000
Percentiles
25 302.7500
50 749.0000
75 1425.0000
b) construct a boxplot, marking any outliers
Solution
The two have be chosen since they are less affected by outliers or by a skewed dataset like the
one above.
Q5.
The following data give the number of workers (in thousand) employed by a small companies in all 50
states of USA.
786 128 930 476 6800 981 759 171 2900 1500
253 259 2600 1300 642 588 734 853 292 1100
1500 2000 1200 452 1200 210 383 402 302 1800
319 3800 1600 161 2300 645 736 2500 238 739
189 1000 3800 430 162 1400 1200 303 1300 123
For the above data, answer the following questions by hand or using SPSS. Include your calculations or
the SPSS output.
a) find the mean, median, Q1, Q3 , and IQR
Solution
Statistics
Number of workers (in thousand)
N Valid 50
Missing 0
Mean 1128.9200
Median 749.0000
Percentiles
25 302.7500
50 749.0000
75 1425.0000
b) construct a boxplot, marking any outliers
Solution
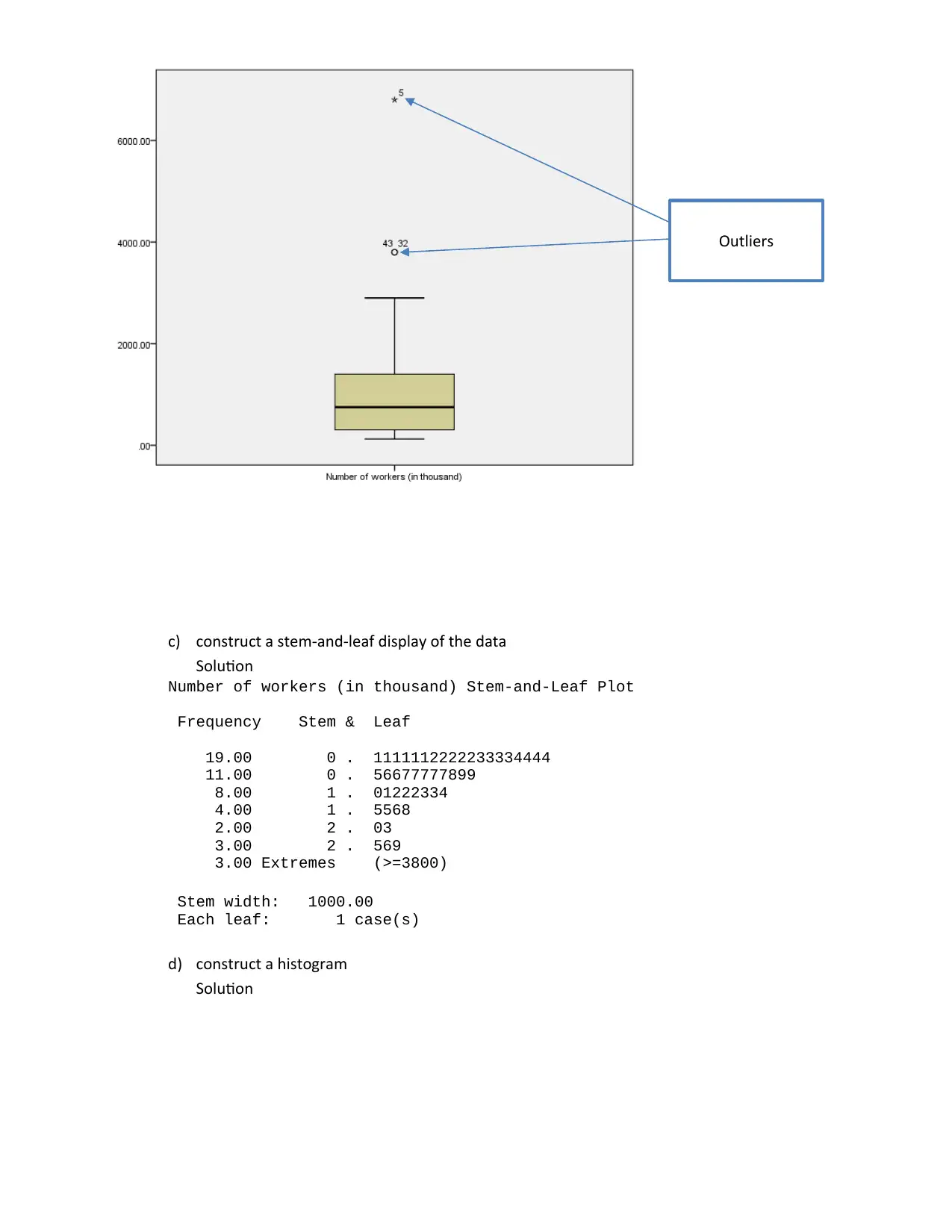
c) construct a stem-and-leaf display of the data
Solution
Number of workers (in thousand) Stem-and-Leaf Plot
Frequency Stem & Leaf
19.00 0 . 1111112222233334444
11.00 0 . 56677777899
8.00 1 . 01222334
4.00 1 . 5568
2.00 2 . 03
3.00 2 . 569
3.00 Extremes (>=3800)
Stem width: 1000.00
Each leaf: 1 case(s)
d) construct a histogram
Solution
Outliers
Solution
Number of workers (in thousand) Stem-and-Leaf Plot
Frequency Stem & Leaf
19.00 0 . 1111112222233334444
11.00 0 . 56677777899
8.00 1 . 01222334
4.00 1 . 5568
2.00 2 . 03
3.00 2 . 569
3.00 Extremes (>=3800)
Stem width: 1000.00
Each leaf: 1 case(s)
d) construct a histogram
Solution
Outliers
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
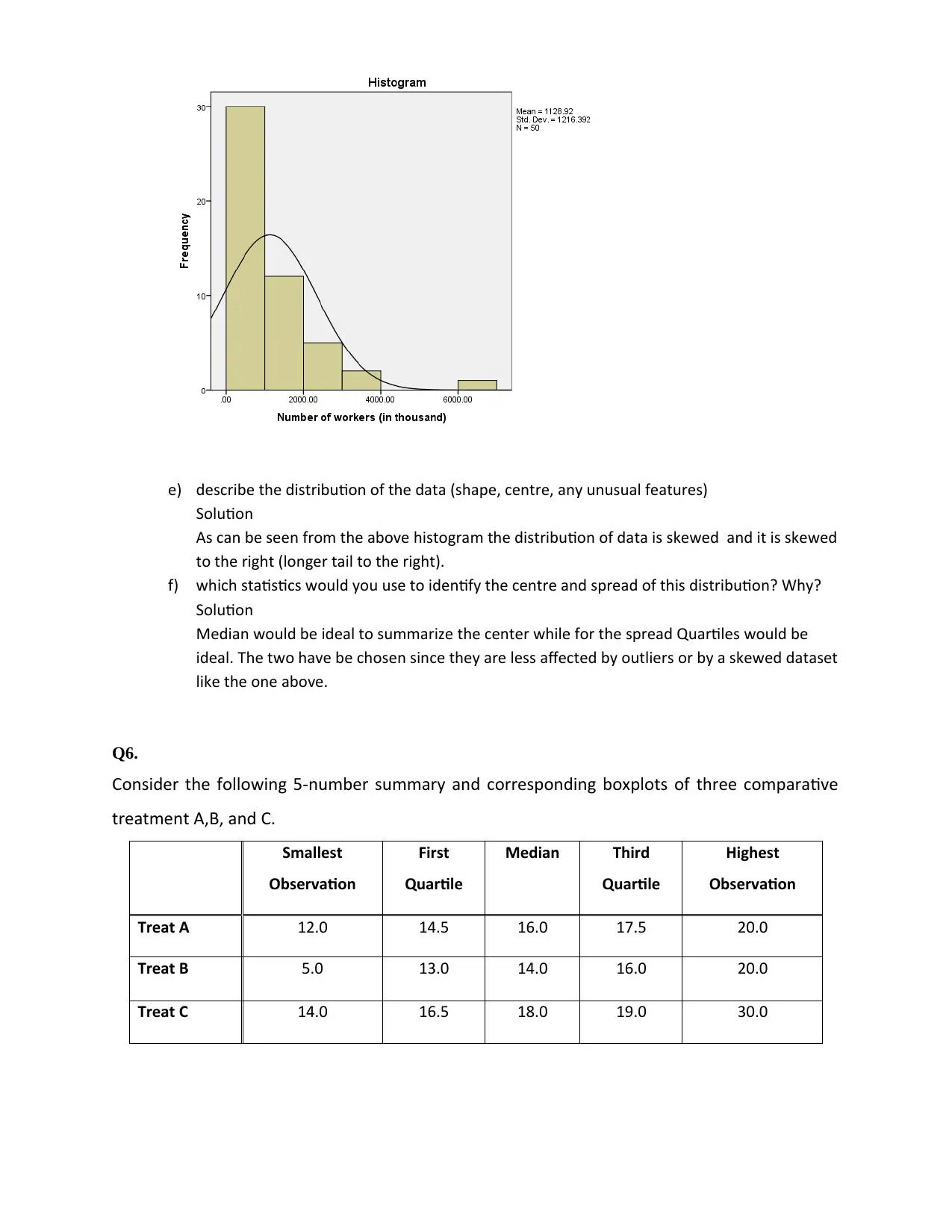
e) describe the distribution of the data (shape, centre, any unusual features)
Solution
As can be seen from the above histogram the distribution of data is skewed and it is skewed
to the right (longer tail to the right).
f) which statistics would you use to identify the centre and spread of this distribution? Why?
Solution
Median would be ideal to summarize the center while for the spread Quartiles would be
ideal. The two have be chosen since they are less affected by outliers or by a skewed dataset
like the one above.
Q6.
Consider the following 5-number summary and corresponding boxplots of three comparative
treatment A,B, and C.
Smallest
Observation
First
Quartile
Median Third
Quartile
Highest
Observation
Treat A 12.0 14.5 16.0 17.5 20.0
Treat B 5.0 13.0 14.0 16.0 20.0
Treat C 14.0 16.5 18.0 19.0 30.0
Solution
As can be seen from the above histogram the distribution of data is skewed and it is skewed
to the right (longer tail to the right).
f) which statistics would you use to identify the centre and spread of this distribution? Why?
Solution
Median would be ideal to summarize the center while for the spread Quartiles would be
ideal. The two have be chosen since they are less affected by outliers or by a skewed dataset
like the one above.
Q6.
Consider the following 5-number summary and corresponding boxplots of three comparative
treatment A,B, and C.
Smallest
Observation
First
Quartile
Median Third
Quartile
Highest
Observation
Treat A 12.0 14.5 16.0 17.5 20.0
Treat B 5.0 13.0 14.0 16.0 20.0
Treat C 14.0 16.5 18.0 19.0 30.0
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

A B C
5 10 15 20 25 30
Figure 1: Response of Three Treatments
Treatment Groups
Response
L
L
L
M
M
M
T
T
T
Outlier
Outlier
L=First quartile
M=Median
T=Third Quartile
Write few sentences (about shapes and outliers) of these boxplots.
Solution
About A
The median for A is about 16; there are no outliers in A and the distribution for A seems to follow a
normal distribution.
About B
The median for B is about 14; there are few outliers at the lower end in B and the distribution for B
seems to be skewed to the right (positively skewed).
About C
The median for C is about 18; there are no outliers in C and the distribution for C seems to be skewed to
the left (negatively skewed).
Q7.
The mean life of a certain brand of auto batteries is 44 months with a standard deviation of 3 months.
Assume that a Normal model can be applied.
a) Draw the model for the life of the auto batteries. Clearly label it, showing what the 68-95-99.7
rule predicts.
Solution
Let X denote the battery life that follow the normal distribution with mean 44 and the
standard deviation 3. That is, μ=44∧σ =3.
The values of the X-scores are obtained below:
According to the 68-95-99.7 rule,
The x-scores within one standard deviation of the mean is,
[ μ−σ , μ+ σ ] = [ 44−3 , 44+3 ]= [ 41 , 47 ]
The x-scores within two standard deviations of the mean is,
5 10 15 20 25 30
Figure 1: Response of Three Treatments
Treatment Groups
Response
L
L
L
M
M
M
T
T
T
Outlier
Outlier
L=First quartile
M=Median
T=Third Quartile
Write few sentences (about shapes and outliers) of these boxplots.
Solution
About A
The median for A is about 16; there are no outliers in A and the distribution for A seems to follow a
normal distribution.
About B
The median for B is about 14; there are few outliers at the lower end in B and the distribution for B
seems to be skewed to the right (positively skewed).
About C
The median for C is about 18; there are no outliers in C and the distribution for C seems to be skewed to
the left (negatively skewed).
Q7.
The mean life of a certain brand of auto batteries is 44 months with a standard deviation of 3 months.
Assume that a Normal model can be applied.
a) Draw the model for the life of the auto batteries. Clearly label it, showing what the 68-95-99.7
rule predicts.
Solution
Let X denote the battery life that follow the normal distribution with mean 44 and the
standard deviation 3. That is, μ=44∧σ =3.
The values of the X-scores are obtained below:
According to the 68-95-99.7 rule,
The x-scores within one standard deviation of the mean is,
[ μ−σ , μ+ σ ] = [ 44−3 , 44+3 ]= [ 41 , 47 ]
The x-scores within two standard deviations of the mean is,
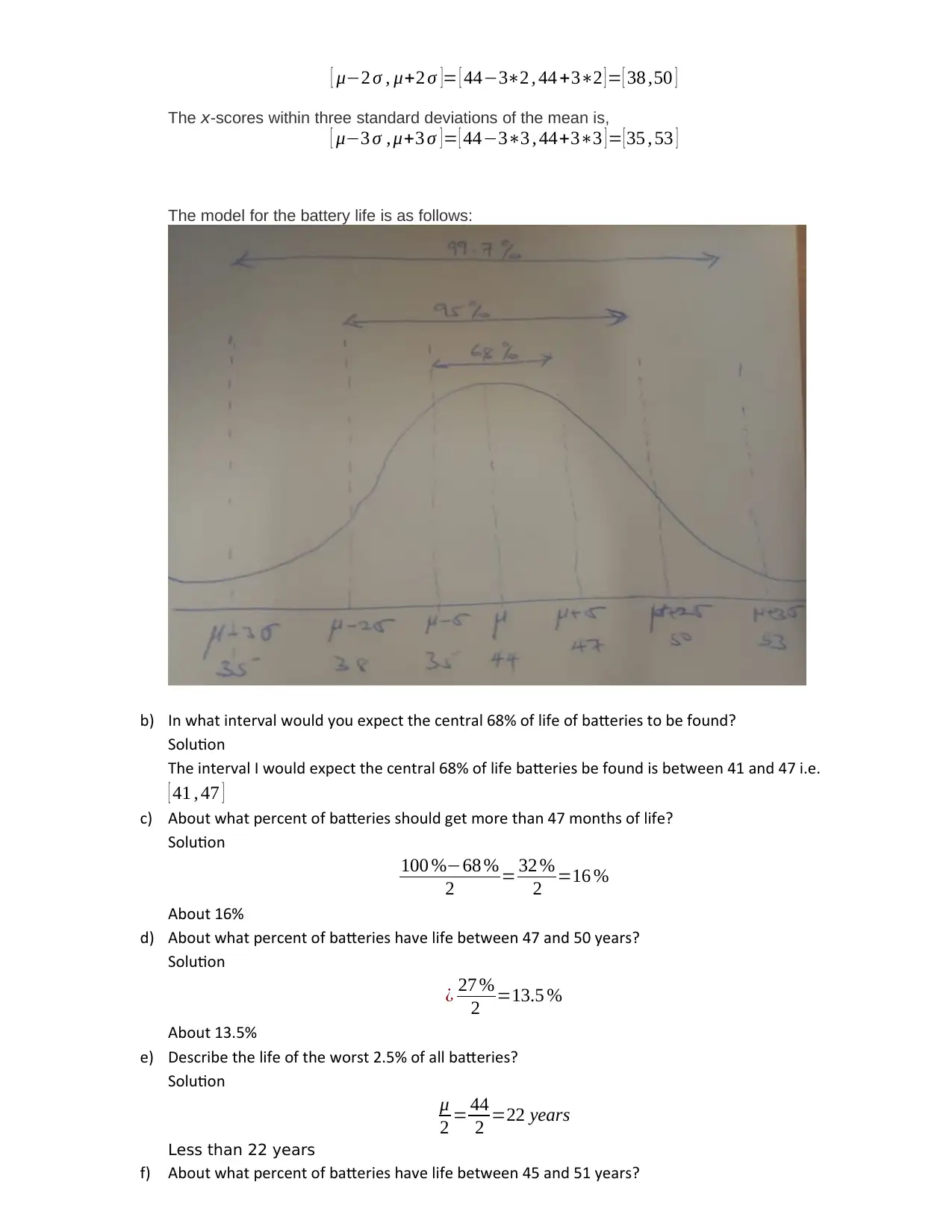
[ μ−2 σ , μ+2 σ ]= [ 44−3∗2 , 44 +3∗2 ] = [ 38 ,50 ]
The x-scores within three standard deviations of the mean is,
[ μ−3 σ , μ+3 σ ]= [ 44−3∗3 , 44+3∗3 ] = [ 35 , 53 ]
The model for the battery life is as follows:
b) In what interval would you expect the central 68% of life of batteries to be found?
Solution
The interval I would expect the central 68% of life batteries be found is between 41 and 47 i.e.
[ 41 , 47 ]
c) About what percent of batteries should get more than 47 months of life?
Solution
100 %−68 %
2 = 32 %
2 =16 %
About 16%
d) About what percent of batteries have life between 47 and 50 years?
Solution
¿ 27 %
2 =13.5 %
About 13.5%
e) Describe the life of the worst 2.5% of all batteries?
Solution
μ
2 = 44
2 =22 years
Less than 22 years
f) About what percent of batteries have life between 45 and 51 years?
The x-scores within three standard deviations of the mean is,
[ μ−3 σ , μ+3 σ ]= [ 44−3∗3 , 44+3∗3 ] = [ 35 , 53 ]
The model for the battery life is as follows:
b) In what interval would you expect the central 68% of life of batteries to be found?
Solution
The interval I would expect the central 68% of life batteries be found is between 41 and 47 i.e.
[ 41 , 47 ]
c) About what percent of batteries should get more than 47 months of life?
Solution
100 %−68 %
2 = 32 %
2 =16 %
About 16%
d) About what percent of batteries have life between 47 and 50 years?
Solution
¿ 27 %
2 =13.5 %
About 13.5%
e) Describe the life of the worst 2.5% of all batteries?
Solution
μ
2 = 44
2 =22 years
Less than 22 years
f) About what percent of batteries have life between 45 and 51 years?
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Solution
About 15%
¿ 30 %
2 =15 %
g) Find the life of the best 7% of all batteries?
Solution
μ+6=44 +6 50 years
50 years
About 15%
¿ 30 %
2 =15 %
g) Find the life of the best 7% of all batteries?
Solution
μ+6=44 +6 50 years
50 years
1 out of 10
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.
