Statistics Assignment 4 with Solutions and Answers

Get Statistics Assignment 4 with solutions and answers for STAT-101 course. Includes multiple choice questions, essay type questions, and one-way ANOVA table. Download now from Desklib.

Assignment NO. 4
STATISTICS (STAT-101)
Answer all the Questions on the same question paper.
Section-I
State whether the following statements are True or False.
1. The hypothesis that an analyst is trying to prove is called the alternative hypothesis.
TRUE
2. One-way ANOVA is used when analyzing the difference between more than two
population means. TRUE
3. If r = 0.9, then r 2 = 0.81, which means that 19% of the total variation in y remains
unexplained. TRUE
4. The chi-square goodness-of-fit test cannot be used to test for normality. FALSE
5. If x and y have a strong positive linear correlation, r is close to 0. FALSE
6. A test of independence CHI-SQUARE tests the null hypothesis that in a contingency
table, the row and column variables are independent. TRUE
Section-II
Multiple choice questions.
1. Which of the following is true of the null and alternative hypotheses?
a. Exactly one hypothesis must be true - TRUE
b. both hypotheses must be true
c. It is possible for both hypotheses to be true
d. It is possible for neither hypothesis to be true
2. The form of the alternative hypothesis can be:
a. one-tailed
b. two-tailed
c. neither one nor two-tailed
d. one or two-tailed - TRUE
3. The value set for is known as:
a. the rejection level
b. the acceptance level

c. the significance level - TRUE
d. the error in the hypothesis test
4. The ANOVA test is based on which assumptions?
I. the sample are randomly selected
II. the population variances are all equal to some common variance
III. the populations are normally distributed
IV. the populations are statistically significant
a. All of the above
b. II and III only
c. I, II, and III only
d. I, and III only
5. The variance within samples (S2p) for the variances 4, 2, and 6 is equal to:
a. 4
b. 5
c. 6
d. None -TRUE
6. A regression between foot length (response variable in cm) and height (explanatory
variable in inches) for 33 students resulted in the following regression equation: yˆ =
10.9 + 0.23 x. One student in the sample was 73 inches tall then the predicted foot
length for this student is. [y^ = 10.9 + 0.23 *(73)]
a. 17.57 cm
b. 27.69 cm - TRUE
c. 29 cm
d. 33 cm
Page 2 of 7

Section-III
Answer the following Essay Type Question
1. The time x in years that an employee spent at a company and the employee’s hourly pay,
y, for 5 employees are listed in the table below.
A-Calculate and interpret the correlation coefficient r.
B-Find the Regression equation. Include a plot of the data in your discussion.
X Y
5 25
3 20
4 21
10 35
15 38
A. Solution:
Correlation coefficient [r ]= 1
n−1 [ ∑ ∑ ( x−xmean )∗( y− ymean)
sx∗s y ]
n=5
Mean of X =5+ 3+4 +10+15
5 =7.4
Mean of Y =25+20+ 21+ 35+38
5 =27.8
X Y X-X_mean Y-Y_mean Squared X
deviations
Squared Y
deviations
(X-X_mean) * (Y-
Y_mean)
5 25 -2.4 -2.8 5.76 7.84 6.72
3 20 -4.4 -7.8 19.36 60.84 34.32
4 21 -3.4 -6.8 11.56 46.24 23.12
10 35 2.6 7.2 6.76 51.84 18.72
15 38 7.6 10.2 57.76 104.04 77.52
7.4 27.8 SUM 101.2 270.8 160.4
Standard deviation of X (sX )= √ ∑ ( X −Xmean )2
5−1
¿ √ 101.2
4 =5.03
Standard deviation of Y (sY )= √∑ ( Y −Y mean )2
5−1
¿ √ 270.8
4 =8.23
Correlation ( r )= 1
4 [ 160.4
5.03∗8.23 ] Page 3 of 7

¿ 0.9689
There is a very strong correlation (0.9689) between the time (in years) employees spend in a
company and their hourly pay.
B. Solution
The regression equation is y=bx+a
Where
a=¿ ¿
b=n ¿ ¿
X Y X^2 Y^2 XY
1 5 25 25 625 125
2 3 20 9 400 60
3 4 21 16 441 84
4 10 35 100 1225 350
5 15 38 225 1444 570
Total 37 139 375 4135 1189
a= ( 139∗375 ) −(37∗1189)
5(375−372 )
¿−1.6362
b= ( 5∗1189 ) −(37∗139)
( 5∗375 ) −372
¿ 1.585
y=1585 x−1.6362
2 4 6 8 10 12 14 16
0
5
10
15
20
25
30
35
40
Time in Years
Hourly Pay
Page 4 of 7

2. A- Use a 0.01 significance level to test the claim that the proportion of men who plan to
vote in the next election is the same as the proportion of women who plan to vote. 300
men and 300 women were randomly selected and asked whether they planned to vote in
the next election. The result is shown below:
Proportion of men( p1 )=170
300 =0.567
Proportion of women ( p2)=185
300 =0.617
overall proportion ¿
Null hypothesis: No difference in proportions between males and females (P1=P2)
Alternative hypothesis: There is a significant difference in proportions between males
and females. (P1 ≠ P2)
Z statistic= ( p1−p2)
√ p¿ (1− p¿)∗(n 1+n 2)
n 1 n 2
¿ 0.567−0.617
√0.592 ( 0.408 )∗( 600
90000 )
¿ −0.05
0.04012 =−1.24626
The p−value=0.1056
The p-value is greater than the significance level (0.01), hence concluding that there is no
difference in proportions for males and females who plan to vote in the next elections.
B- According to Benford's law, a variety of different data sets includes numbers with leading
(first) digits that follow the distribution shown in the nine row of Table 1. The bottom row
lists the frequencies of leading digits of the populations of all 120 countries from New York
and California combined. Test the claim that those 120 countries have populations with
leading digits that follow Benford’s law.
Leading Benford’slaw: CA and
Page 5 of 7
Men women Total
Plan to vote 170 185 355
Do not plan to vote 130 115 245
Total 300 300 600

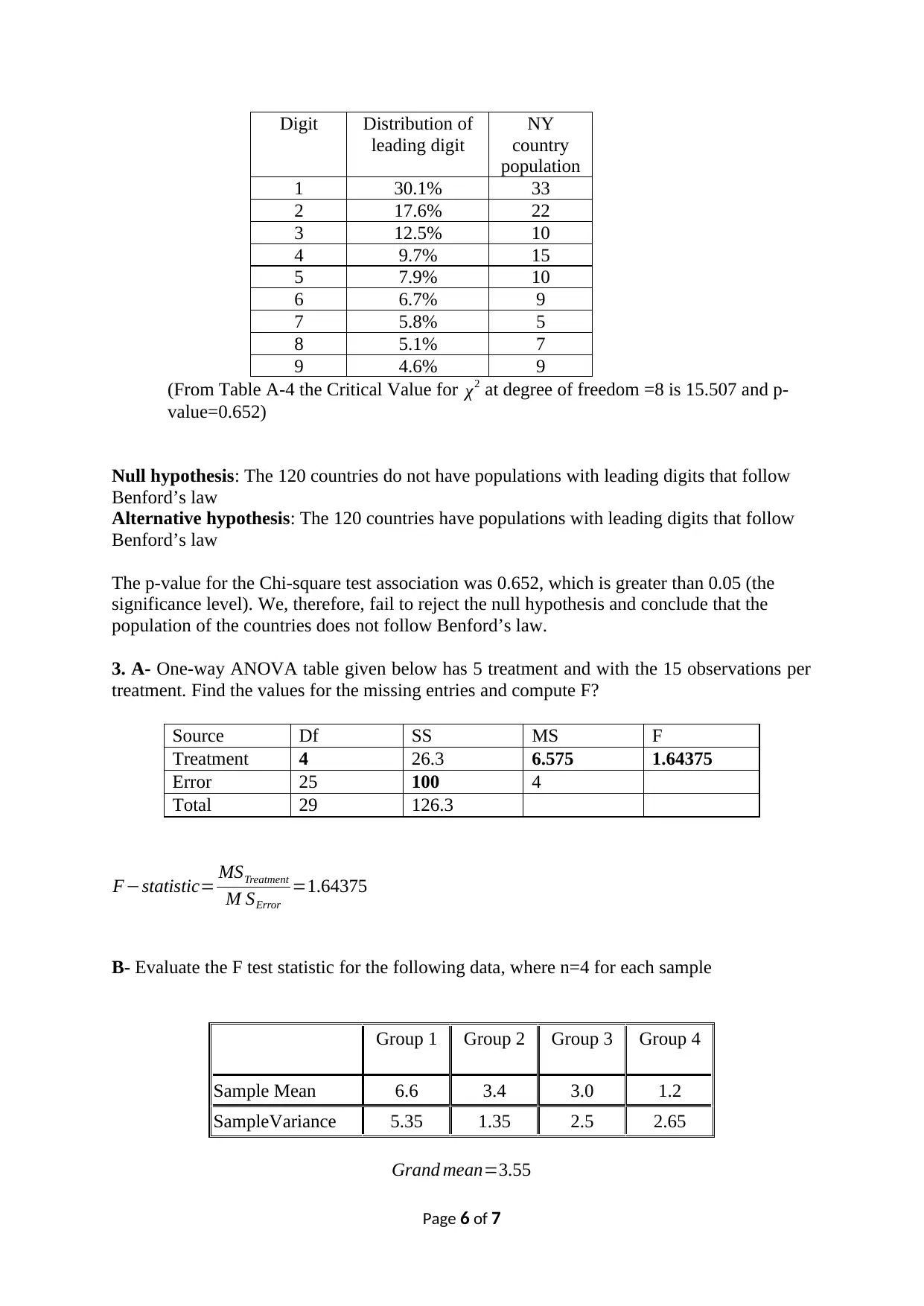
Digit Distribution of
leading digit
NY
country
population
1 30.1% 33
2 17.6% 22
3 12.5% 10
4 9.7% 15
5 7.9% 10
6 6.7% 9
7 5.8% 5
8 5.1% 7
9 4.6% 9
(From Table A-4 the Critical Value for χ2 at degree of freedom =8 is 15.507 and p-
value=0.652)
Null hypothesis: The 120 countries do not have populations with leading digits that follow
Benford’s law
Alternative hypothesis: The 120 countries have populations with leading digits that follow
Benford’s law
The p-value for the Chi-square test association was 0.652, which is greater than 0.05 (the
significance level). We, therefore, fail to reject the null hypothesis and conclude that the
population of the countries does not follow Benford’s law.
3. A- One-way ANOVA table given below has 5 treatment and with the 15 observations per
treatment. Find the values for the missing entries and compute F?
Source Df SS MS F
Treatment 4 26.3 6.575 1.64375
Error 25 100 4
Total 29 126.3
F−statistic= MSTreatment
M SError
=1.64375
B- Evaluate the F test statistic for the following data, where n=4 for each sample
Group 1 Group 2 Group 3 Group 4
Sample Mean 6.6 3.4 3.0 1.2
SampleVariance 5.35 1.35 2.5 2.65
Grand mean=3.55
Page 6 of 7

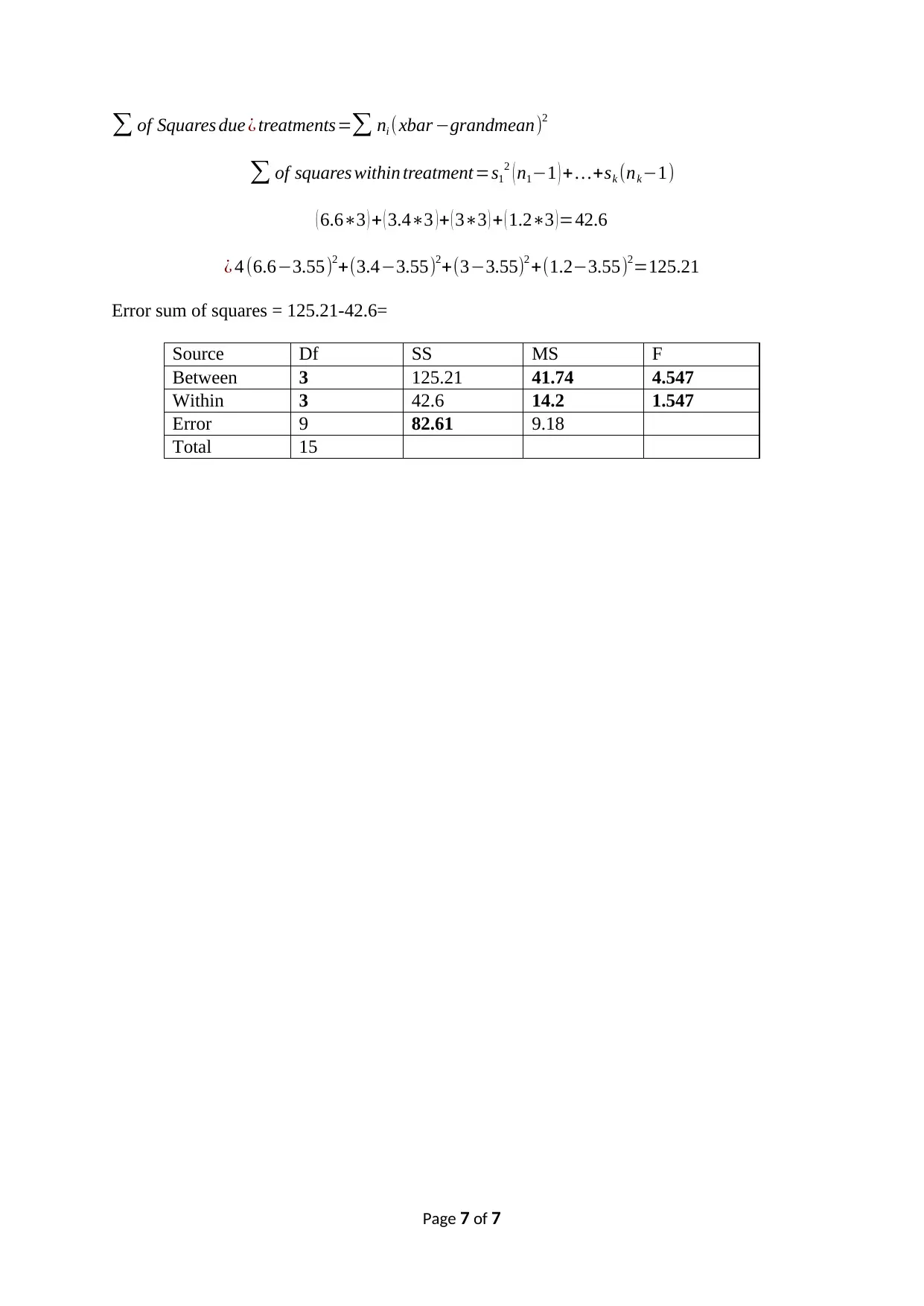
∑ of Squares due ¿ treatments=∑ ni (xbar −grandmean)2
∑ of squares within treatment=s1
2 ( n1−1 ) +…+sk (nk−1)
( 6.6∗3 ) + ( 3.4∗3 )+ ( 3∗3 ) + ( 1.2∗3 )=42.6
¿ 4 (6.6−3.55)2+(3.4−3.55)2+(3−3.55)2 +(1.2−3.55)2=125.21
Error sum of squares = 125.21-42.6=
Source Df SS MS F
Between 3 125.21 41.74 4.547
Within 3 42.6 14.2 1.547
Error 9 82.61 9.18
Total 15
Page 7 of 7