Statistical Analysis and Regression

The provided document is a collection of statistical analyses performed on various data sets related to yearly growth percentage across different geographic regions. It includes an independent sample t-test, one-way ANOVA with Tukey HSD, normality tests using Kolmogorov-Smirnova and Shapiro-Wilk methods, regression analysis with correlation between specific gravity and osmolarity, and further normality testing. The results provide insights into the mean differences across regions, homogeneity of subsets, significance of correlations, and the standard error of the estimate for the regression model.

STATISTICS
1

Table of Contents
QUESTION 1.......................................................................................................................................1
A. Justifying type of samples...........................................................................................................1
B. Appropriate test to examine 1-carat effect..................................................................................1
C. Reporting 95% confidence interval for difference in average prices..........................................1
D. Stating and checking assumptions..............................................................................................1
QUESTION 2.......................................................................................................................................4
A. Examining significant difference in the yearly growth percentage across three regions............4
B. Perform post-hoc tests.................................................................................................................5
C. 95% pair-wise CI for mean difference in yearly growth % in Antarctic Peninsula and
Himalayas........................................................................................................................................5
D. Stating and checking the assumptions for analysis.....................................................................5
QUESTION 3.......................................................................................................................................9
A. Scatter Plot with fitted regression line........................................................................................9
B. Assessing linear relationship between Osmolality and specific gravity.....................................9
C. Assumptions for regression.......................................................................................................10
D. Equation for estimated regression line and interpreting slope coefficient................................10
E. Predicting osmolality for USG value of 1.025..........................................................................11
F. Write down R2 value for regression and interpretation..............................................................11
G. Sensible or not to use R2 value to predict osmolality...............................................................11
REFERENCES...................................................................................................................................12
APPENDIX....................................................................................................................................13
Appendix: 1. Independent sample t-test........................................................................................13
Appendix: 2. Normality Test..........................................................................................................13
Appendix: 3. One-Way ANOVA....................................................................................................13
Appendix: 4. Post Hoc tests...........................................................................................................14
Appendix: 5. Normality test...........................................................................................................14
Appendix: 6. Regression & Correlation........................................................................................15
Appendix: 7. Normality Test..........................................................................................................16
2

QUESTION 1
A. Justifying type of samples
Drawing out a random sample of 30 diamonds less than 1 carat and 30 diamonds above 1-
carat weight are independent samples because in both of these, different units had selected with
having different carat weight.
B. Appropriate test to examine 1-carat effect
μ0: Average price of carat diamond is not higher than sub-carat diamonds.
μ1: Average price of carat diamond is higher than sub-carat diamonds.
Test significance: 0.05 or 5%
Independent sample T-test
Null distribution: F distribution
Results:
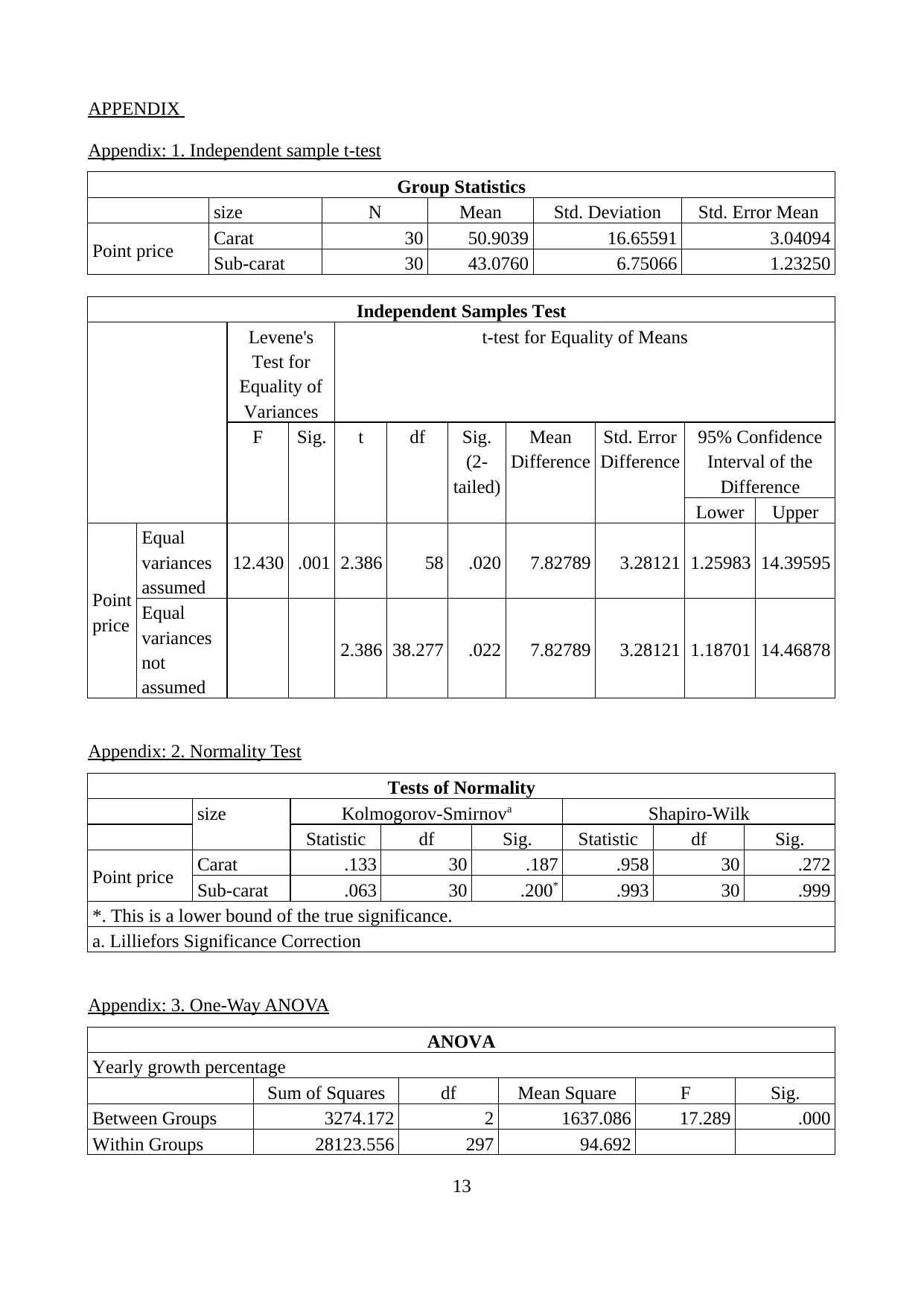
Appendix 1
Group Statistics table reflect that Carat size diamond’s average price is 50.90 greater than
the price of ‘Sub Carat’ diamond size with an average price of just 43.07. The statistical
significance of looked difference is tested through independent sample t-test. In this, Leneve’s test
statistics reflect sig value of 0.001<0.05 which states that popular variance in both the groups are
not equal and found sig. level t(38.27) = 2.386, p = 0.022<0.05 that reflects significant difference
exists in the diamond price of “carat’ and ‘Sub Carat’ size. Thus, alternative hypothesis accepted
that demonstrates that point price of carat diamonds is higher than sub-carat diamonds due to
existence of 1 carat effect (Koch, 2013).
C. Reporting 95% confidence interval for difference in average prices
The output shows that at 95%, confidence interval for the equal variance not assumed series
is found 1.18 – 14.46 which evident that difference exists in the price of carat and sub-carat
diamond sizes. Thus, the difference in average price between Carat and Sub-carat lies in the range
of 1.18 -14.46. The findings are in line with the lower P value of 0.022 than test statistics of 0.05,
hence, it can be said that CI supports acceptance of alternative hypothesis evidencing the presence
of 1-carat effect (De Winter, 2013).
D. Stating and checking assumptions
 Dependent variable must be measured on continuous scale (ratio or interval). Here point
price satisfies the conditions.
 Independent variable must be independent group that are ‘carat’ and ‘sub-carat’ sizes.
1

 There is no relationship exists between both the samples.
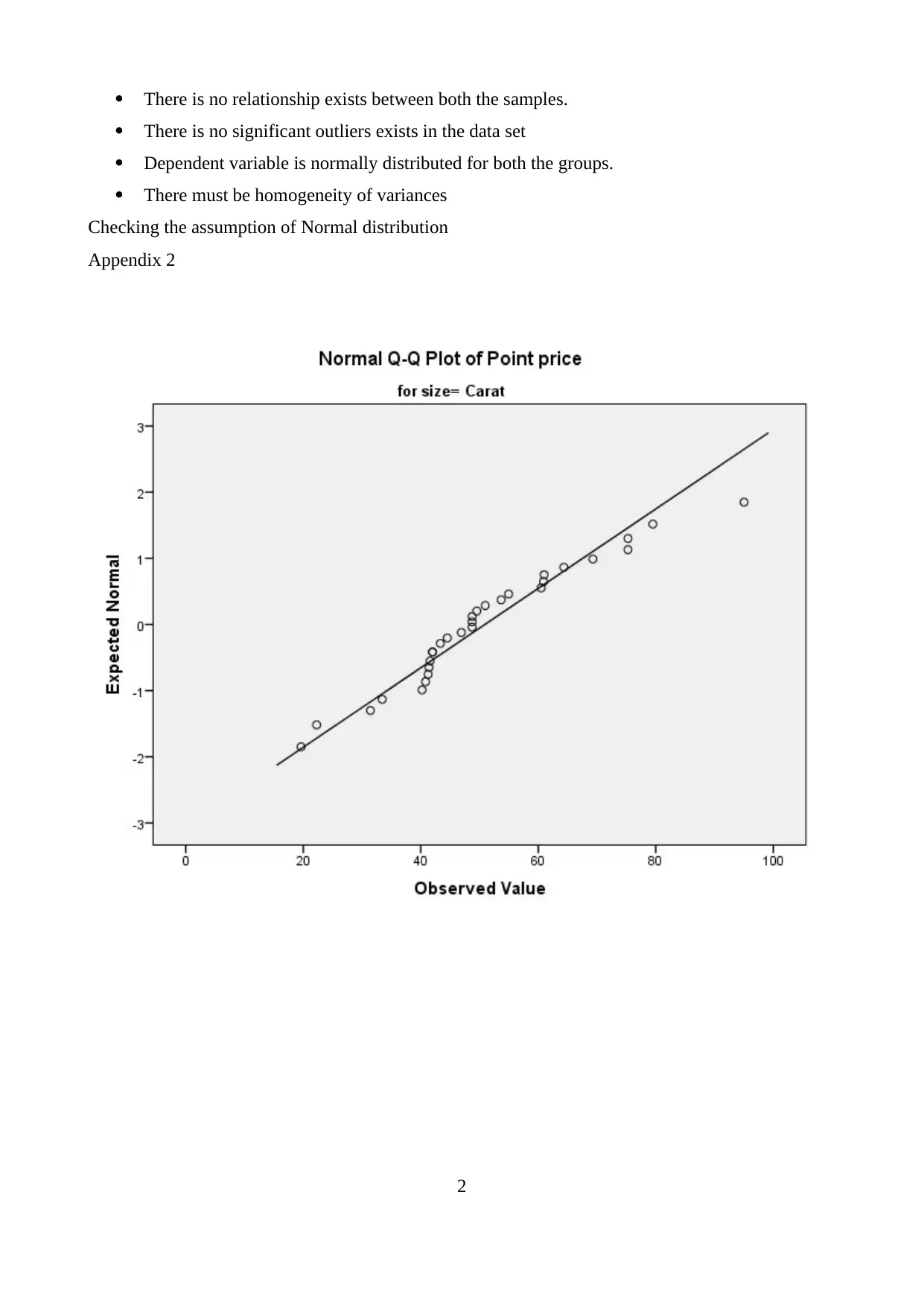
 There is no significant outliers exists in the data set
 Dependent variable is normally distributed for both the groups.
 There must be homogeneity of variances
Checking the assumption of Normal distribution
Appendix 2
2

As the sample size is 30<50, therefore, SW test found more appropriate that found sig. value
(P) of 0.272 and 0.999>0.05 satisfies the assumption of normal distribution data set of Carat and
Sub-carat. Moreover, diagram does not reflect any outliers in the given data set (Jaggia and et.al.,
2016).
3

QUESTION 2
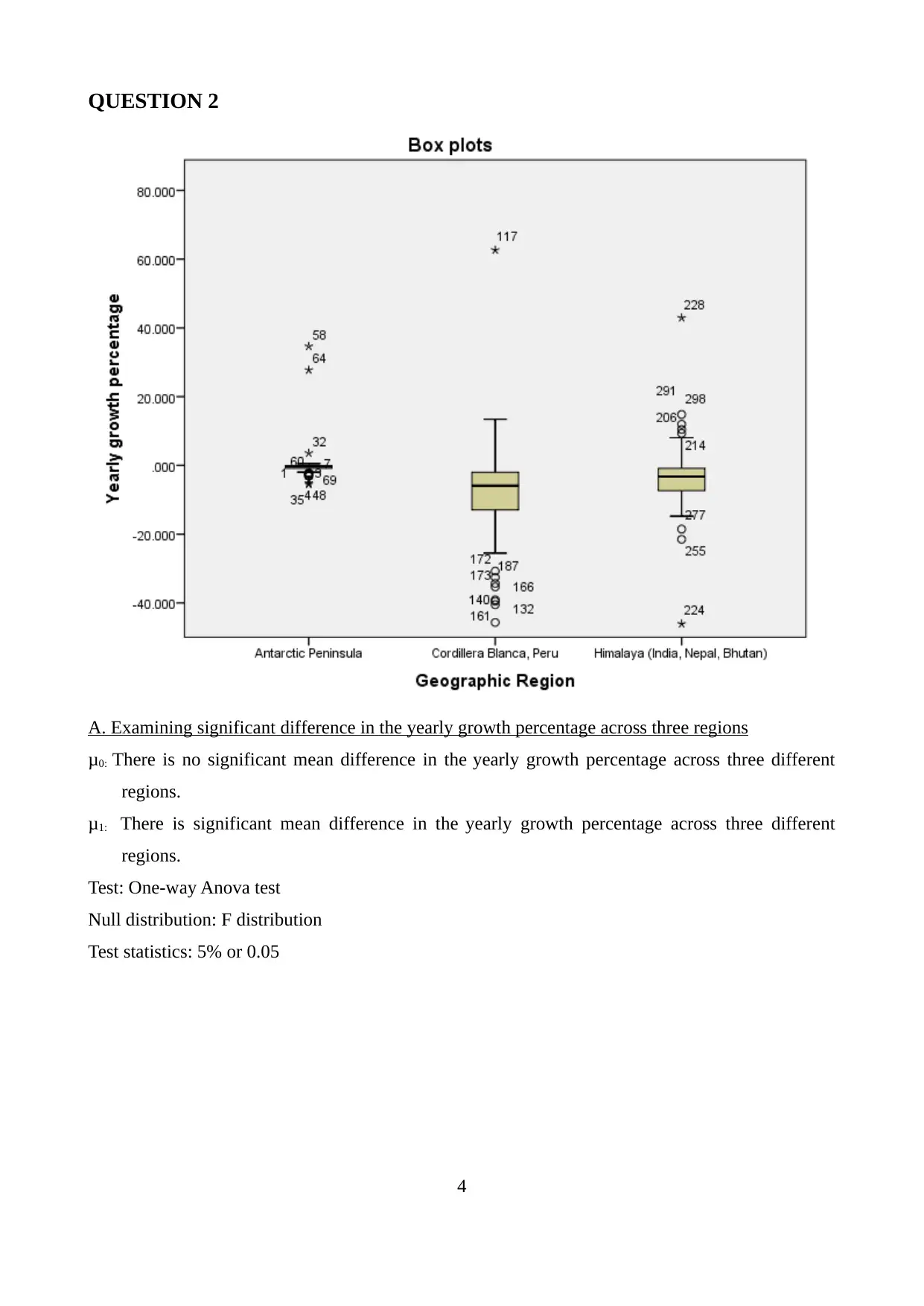
A. Examining significant difference in the yearly growth percentage across three regions
μ0: There is no significant mean difference in the yearly growth percentage across three different
regions.
μ1: There is significant mean difference in the yearly growth percentage across three different
regions.
Test: One-way Anova test
Null distribution: F distribution
Test statistics: 5% or 0.05
4

Appendix 4.
Above results found that sig. value is 0.000<0.05 therefore, alternative hypothesis is true and
there is significant statistical difference exists in the average yearly growth percentage across three
different regions (Siegel, 2016).
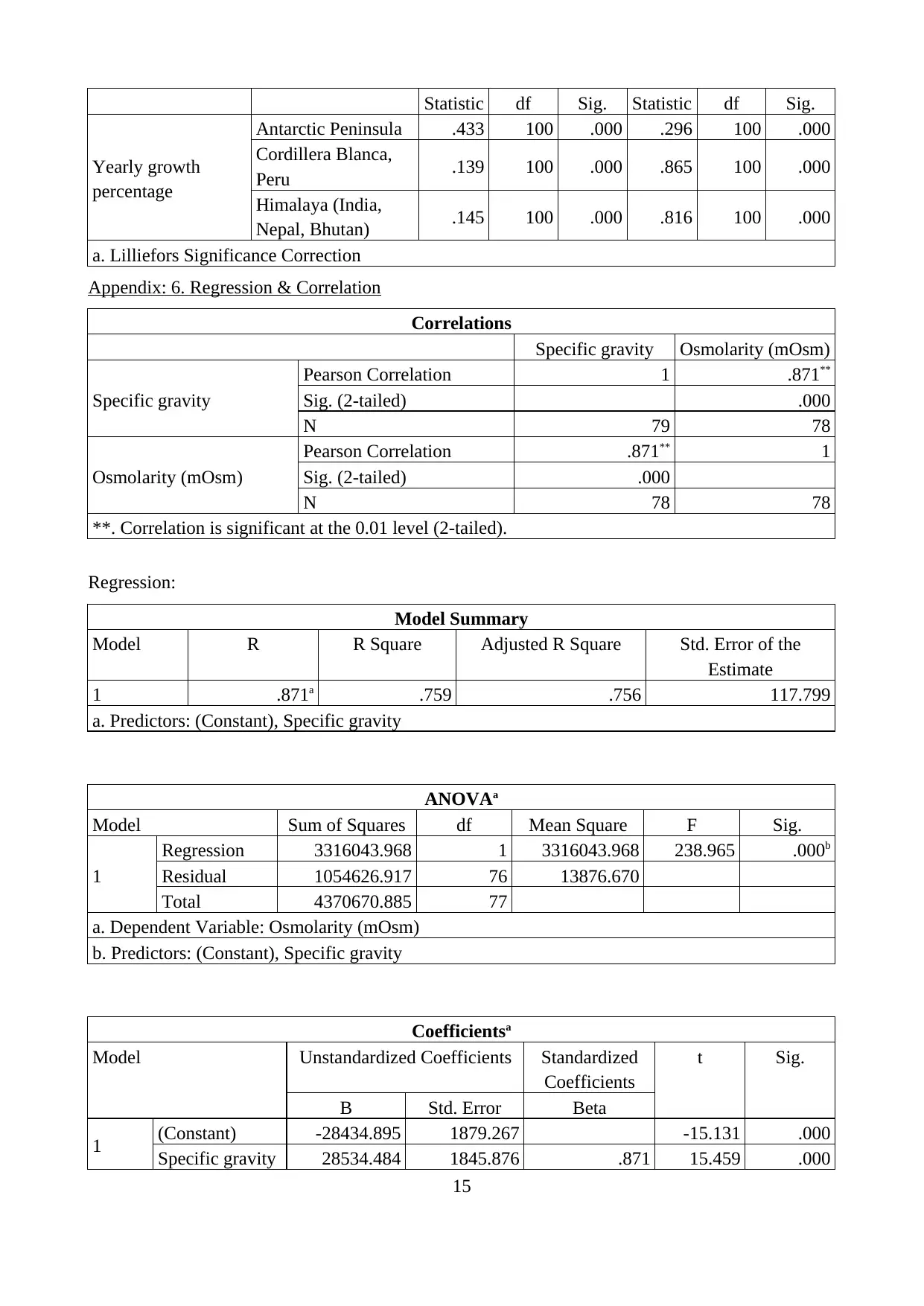
B. Perform post-hoc tests
After looking to the Post Hoc Test results, it is discovered that mean difference in the
average yearly growth percentage in Antarctic Peninsula and Cordillera Blanca, Peru is very high to
8.07 at sig. value of 0.00<0.05 shows higher significant statistical mean difference. Similarly, other
series also reflects significant mean difference as Himalaya and Cordillera Blanca indicates mean
difference of 4.53 at sig value of 0.03<0.05 and Antarctic and Himalaya reflect mean difference of
3.54 at sig value of 0.028<0.05, still, the difference is comparatively lower than that of Antarctic
Peninsula and Cordillera Blanca, Peru.
C. 95% pair-wise CI for mean difference in yearly growth % in Antarctic Peninsula and Himalayas
At 95%, pair-wise confidence interval for mean difference in the yearly growth percentage
in Antarctic Peninsula and Himalayas is found to 0.29873-6.78194 comparatively lower than
difference between Himalaya and Cordillera Blanca, Peru at CI of 1.28-7.77 and Antarctica and
Cordillera Blanca, Peru with CI of 4.83 – 11.31 shows less significant difference.
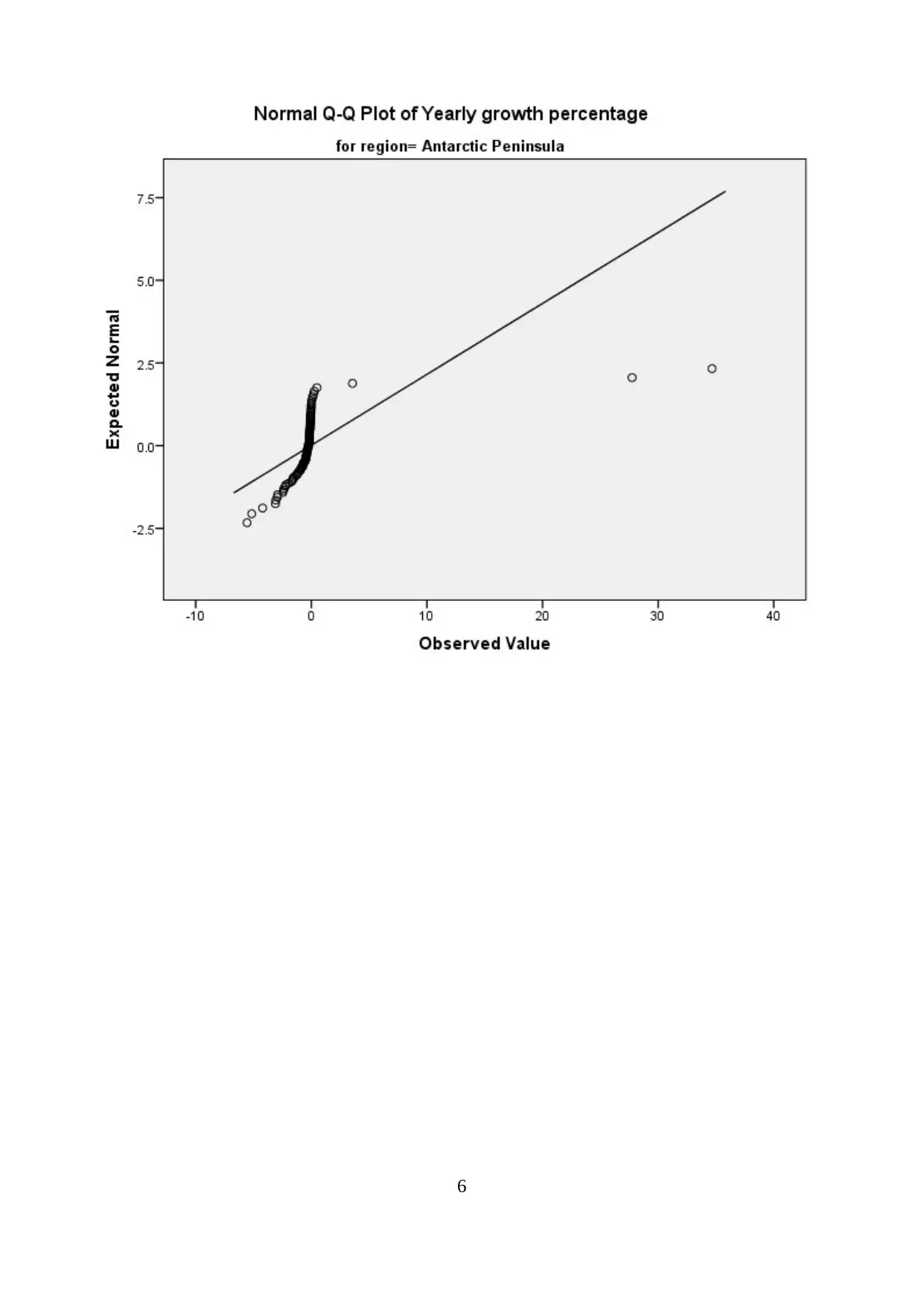
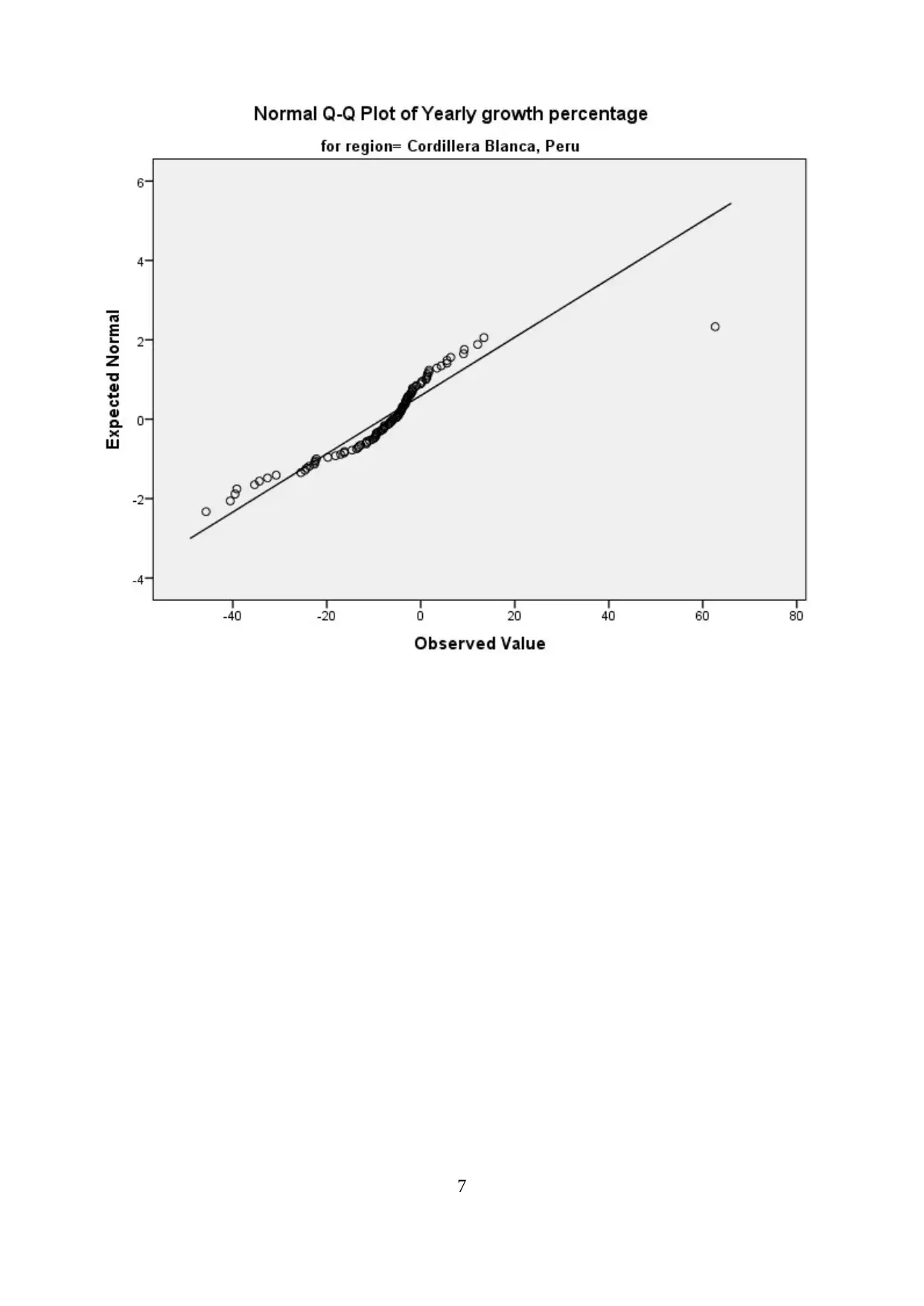
D. Stating and checking the assumptions for analysis
 Dependent variable that is yearly growth percentage is a continuous variable.
 Independent variable that is three different region is categorical variable.
 There is no relationship exists between different random observation of 100 sample unit from
all the regions.
 No significant outliers exist.
 Dependent variable is normally distributed across all the independent series.
Normality Test
Appendix 5.
5

6

7

As per the results, assumption of normal distribution does not found true as KS test reflect
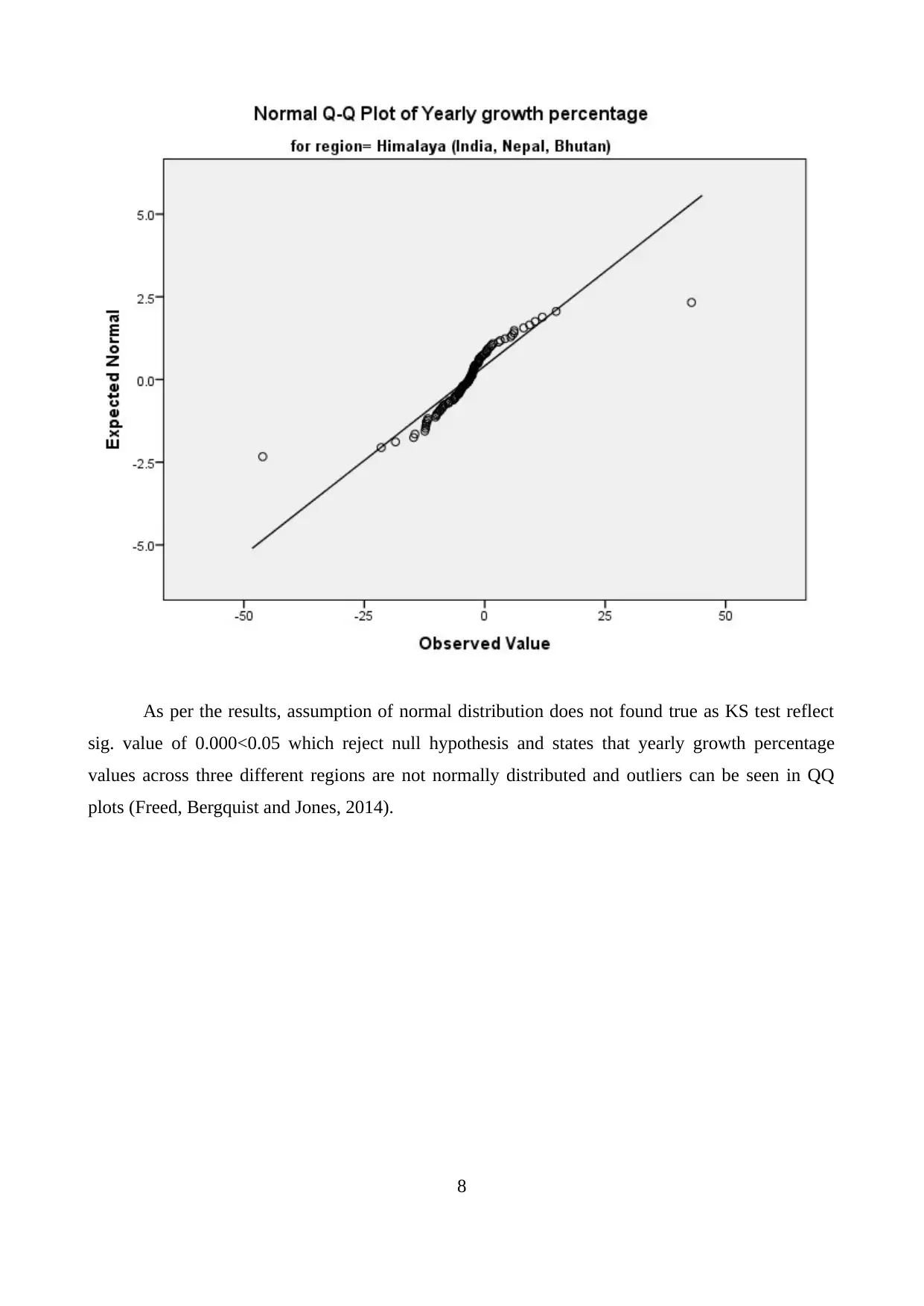
sig. value of 0.000<0.05 which reject null hypothesis and states that yearly growth percentage
values across three different regions are not normally distributed and outliers can be seen in QQ
plots (Freed, Bergquist and Jones, 2014).
8

QUESTION 3
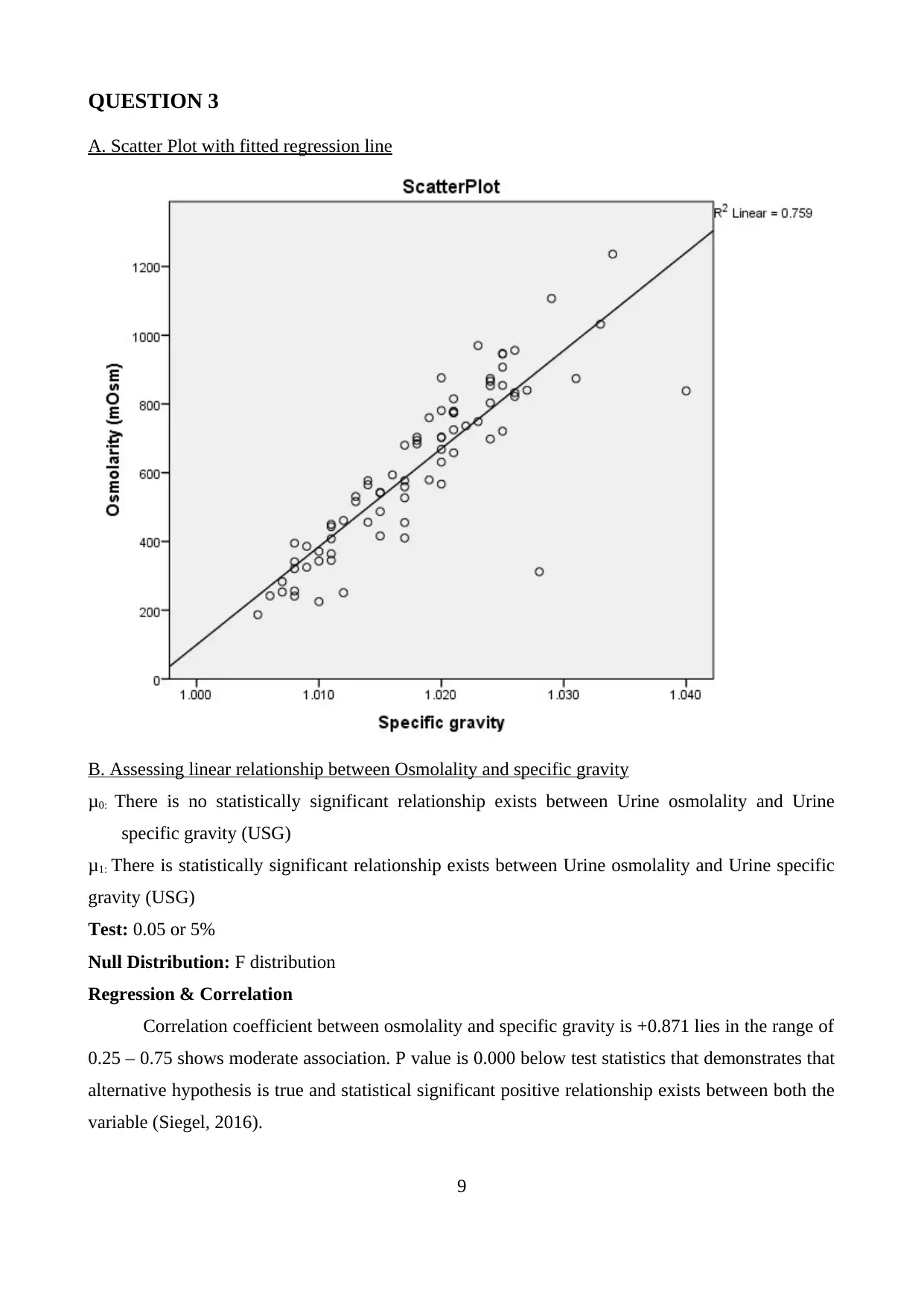
A. Scatter Plot with fitted regression line
B. Assessing linear relationship between Osmolality and specific gravity
μ0: There is no statistically significant relationship exists between Urine osmolality and Urine
specific gravity (USG)
μ1: There is statistically significant relationship exists between Urine osmolality and Urine specific
gravity (USG)
Test: 0.05 or 5%
Null Distribution: F distribution
Regression & Correlation
Correlation coefficient between osmolality and specific gravity is +0.871 lies in the range of
0.25 – 0.75 shows moderate association. P value is 0.000 below test statistics that demonstrates that
alternative hypothesis is true and statistical significant positive relationship exists between both the
variable (Siegel, 2016).
9

C. Assumptions for regression
 Both the variables that are osomolality and specific gravity are measured at continuous level.
 Linear relationship exists between variables
 All the observations are independent from each other.
 There is no significant outliers exists in the dependent variable.
Above QQ plot did not show any outliers.
 Data set is normally distributed
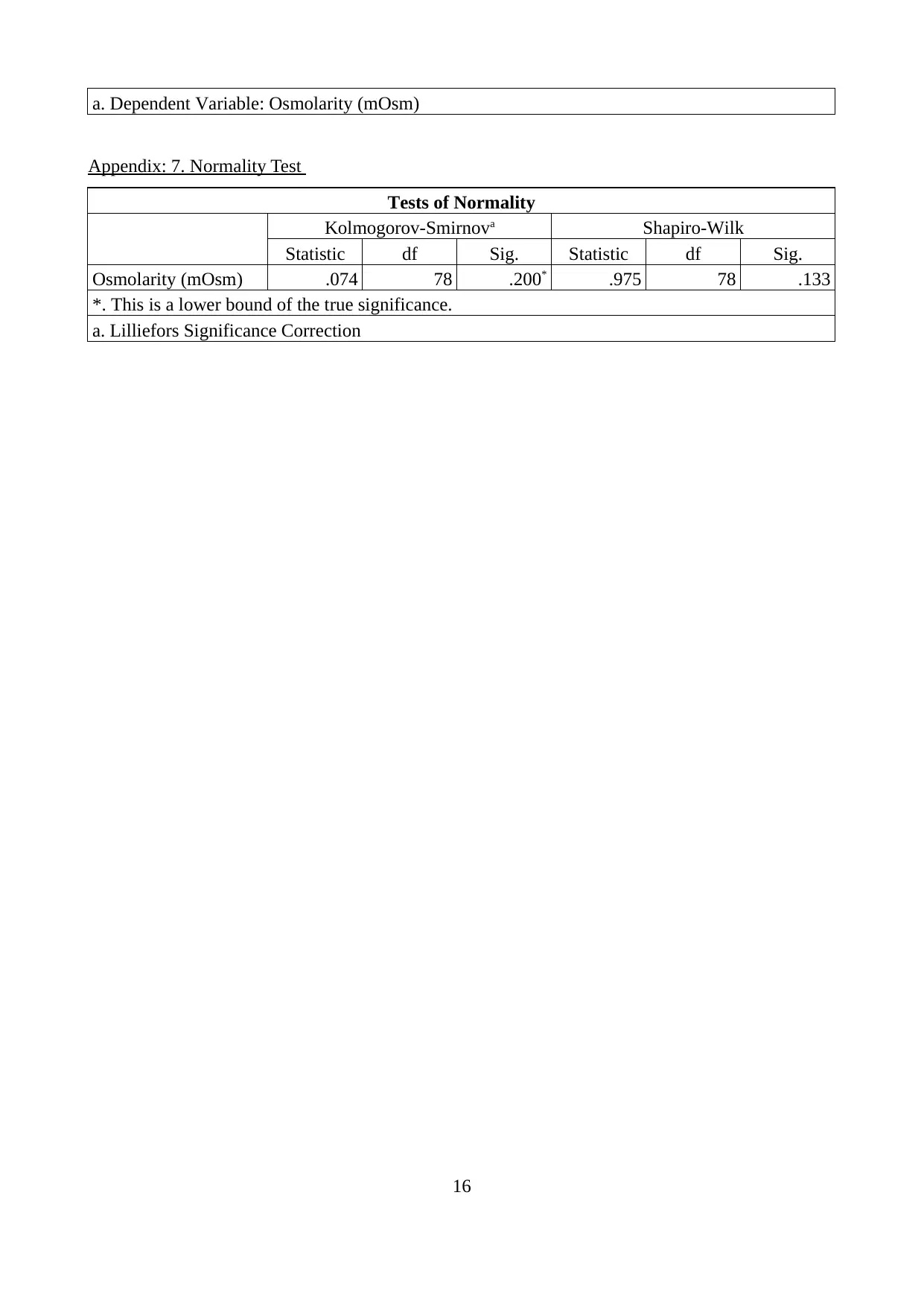
Appendix 7
KS test reflect sig. value of 0.200>0.05 hence, normal distribution assumption proven true.
D. Equation for estimated regression line and interpreting slope coefficient
Regression Equation Y = a + bx
= 28434.895 + 28534.484(USG)
Slope coefficient shows steeepness of regression line. Here, it is found to 28534.484 that
represent that per unit change in independent or predictor variable will bring change in the
10

dependent variable, osmolality by 28534.484.
E. Predicting osmolality for USG value of 1.025
= -28434.895 + 28534.484(USG)
= -28434.895 + 28534.484(1.025)
= 812.95
F. Write down R2 value for regression and interpretation
R2 is a statistical measurement that helps to determine that how close a data set is to the
fitted regression line, called coefficient of determination (Frost, 2013). Regression results present R
square value of 0.759, higher the value always shows that model fits the data set well whereas lower
the value of R2 is problematic and questioned the regression results.
G. Sensible or not to use R2 value to predict osmolality
Here, R2 value is 0.759 that indicates that there it is justifiable to use USG to predict
osmolality and the results will provide approximation of osmolality near around 75.9% values.
11

REFERENCES
Books and Journals
Jaggia, S. and et.al., 2016. Essentials of business statistics: communicating with numbers. McGraw-
Hill Education.
Koch, K.R., 2013. Parameter estimation and hypothesis testing in linear models. Springer Science
& Business Media.
De Winter, J.C., 2013. Using the Student’s t-test with extremely small sample sizes. Practical
Assessment, Research & Evaluation. 18(10). pp.1-12.
Freed, N., Bergquist, T. and Jones, S., 2014. Understanding business statistics. John Wiley & Sons.
Siegel, A., 2016. Practical business statistics. Academic Press.
Online
Frost, J., 2013. Regression Analysis. [Online]. Available through: <
http://blog.minitab.com/blog/adventures-in-statistics-2/regression-analysis-how-do-i-
interpret-r-squared-and-assess-the-goodness-of-fit>.
12

APPENDIX
Appendix: 1. Independent sample t-test
Group Statistics
size N Mean Std. Deviation Std. Error Mean
Point price Carat 30 50.9039 16.65591 3.04094
Sub-carat 30 43.0760 6.75066 1.23250
Independent Samples Test
Levene's
Test for
Equality of
Variances
t-test for Equality of Means
F Sig. t df Sig.
(2-
tailed)
Mean
Difference
Std. Error
Difference
95% Confidence
Interval of the
Difference
Lower Upper
Point
price
Equal
variances
assumed
12.430 .001 2.386 58 .020 7.82789 3.28121 1.25983 14.39595
Equal
variances
not
assumed
2.386 38.277 .022 7.82789 3.28121 1.18701 14.46878
Appendix: 2. Normality Test
Tests of Normality
size Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
Point price Carat .133 30 .187 .958 30 .272
Sub-carat .063 30 .200* .993 30 .999
*. This is a lower bound of the true significance.
a. Lilliefors Significance Correction
Appendix: 3. One-Way ANOVA
ANOVA
Yearly growth percentage
Sum of Squares df Mean Square F Sig.
Between Groups 3274.172 2 1637.086 17.289 .000
Within Groups 28123.556 297 94.692
13

Total 31397.728 299
Appendix: 4. Post Hoc tests
Post Hoc Tests
Multiple Comparisons
Dependent Variable: Yearly growth percentage
Tukey HSD
(I) Geographic
Region
(J) Geographic
Region
Mean
Difference (I-
J)
Std.
Error
Sig. 95% Confidence
Interval
Lower
Bound
Upper
Bound
Antarctic Peninsula
Cordillera Blanca,
Peru 8.071922* 1.376169 .000 4.83032 11.31352
Himalaya (India,
Nepal, Bhutan) 3.540336* 1.376169 .028 .29873 6.78194
Cordillera Blanca,
Peru
Antarctic Peninsula -8.071922* 1.376169 .000 -
11.31352 -4.83032
Himalaya (India,
Nepal, Bhutan) -4.531586* 1.376169 .003 -7.77319 -1.28999
Himalaya (India,
Nepal, Bhutan)
Antarctic Peninsula -3.540336* 1.376169 .028 -6.78194 -.29873
Cordillera Blanca,
Peru 4.531586* 1.376169 .003 1.28999 7.77319
*. The mean difference is significant at the 0.05 level.
Homogeneous Subsets
Yearly growth percentage
Tukey HSD
Geographic Region N Subset for alpha = 0.05
1 2 3
Cordillera Blanca, Peru 100 -8.12758
Himalaya (India, Nepal, Bhutan) 100 -3.59600
Antarctic Peninsula 100 -.05566
Sig. 1.000 1.000 1.000
Means for groups in homogeneous subsets are displayed
a. Uses Harmonic Mean Sample Size = 100.000.
Appendix: 5. Normality test
Tests of Normality
Geographic Region Kolmogorov-Smirnova Shapiro-Wilk
14

Statistic df Sig. Statistic df Sig.
Yearly growth
percentage
Antarctic Peninsula .433 100 .000 .296 100 .000
Cordillera Blanca,
Peru .139 100 .000 .865 100 .000
Himalaya (India,
Nepal, Bhutan) .145 100 .000 .816 100 .000
a. Lilliefors Significance Correction
Appendix: 6. Regression & Correlation
Correlations
Specific gravity Osmolarity (mOsm)
Specific gravity
Pearson Correlation 1 .871**
Sig. (2-tailed) .000
N 79 78
Osmolarity (mOsm)
Pearson Correlation .871** 1
Sig. (2-tailed) .000
N 78 78
**. Correlation is significant at the 0.01 level (2-tailed).
Regression:
Model Summary
Model R R Square Adjusted R Square Std. Error of the
Estimate
1 .871a .759 .756 117.799
a. Predictors: (Constant), Specific gravity
ANOVAa
Model Sum of Squares df Mean Square F Sig.
1
Regression 3316043.968 1 3316043.968 238.965 .000b
Residual 1054626.917 76 13876.670
Total 4370670.885 77
a. Dependent Variable: Osmolarity (mOsm)
b. Predictors: (Constant), Specific gravity
Coefficientsa
Model Unstandardized Coefficients Standardized
Coefficients
t Sig.
B Std. Error Beta
1 (Constant) -28434.895 1879.267 -15.131 .000
Specific gravity 28534.484 1845.876 .871 15.459 .000
15

a. Dependent Variable: Osmolarity (mOsm)
Appendix: 7. Normality Test
Tests of Normality
Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
Osmolarity (mOsm) .074 78 .200* .975 78 .133
*. This is a lower bound of the true significance.
a. Lilliefors Significance Correction
16