Business Math Portfolio: Module on Numerical Skills, Calculations

This portfolio assignment assesses numerical skills, concepts, and techniques in a business context. It is divided into four sections, with Sections 1, 2, and 3 focusing on topics like BODMAS, fractions, ratios, decimals, percentages, and index numbers, incorporating skills audits, in-class activities, and online quizzes. Section 4, worth 55% of the marks, comprises 10 questions. The assignment requires students to demonstrate their ability to apply mathematical concepts to real-life problems, calculate and interpret statistical values including mean, median, mode, and range, and represent data graphically. Students are expected to reflect on their learning experiences and provide evidence of completing online activities. The portfolio emphasizes practical application and understanding of mathematical principles in a business environment.

Coursework/Portfolio Brief
Learning outcomes assessed:
 Apply numerical skills, concepts and techniques in a variety of
business and academic contexts.
 Demonstrate an ability to calculate and interpret statistical values.
 Be able to interpret and process mathematical problems in personal
and professional contexts.
This coursework is worth 100% of the total marks for this module.

MATI3006- Numeracy1 Summer 2017 Coursework Brief
Coursework Instructions
Please read carefully
• Carefully read the module handbook, the marking criteria and the
grade descriptors.
Academic Misconduct
You are responsible for ensuring you understand the policy and
regulations about academic misconduct. You must:
• Complete this work alone except where required or allowed by this
assignment briefing paper and ensure it has not been written or
composed by or with the assistance of any other person.
• Make sure all sentences or passages quoted from other people’s
work in this assignment (with or without trivial changes) are in
quotation marks, and are specifically acknowledged by reference
to the author, work and page.
This portfolio consists of four sections:
Sections 1, 2 and 3 are assessed in ‘pass/fail’ criteria. Sections 1, 2
and 3 combined are worth 45% of the final mark.
For example, if a student completes and passes 5 out of 9 tasks
outlined in Sections 1, 2 and 3 he/she will be given the following
marks:
5 / 9 x 45 = 25
Sections 1, 2 and 3 each consist of 3 tasks:
Task 1 – Skills Audit
Task 2 – In class Activity
Task 3 – Online Activity - students are expected to complete and pass
(40%) relevant online activity/quiz. The results page will need to be
saved (screenshot) and inserted under a relevant area of the
portfolio.

MATI3006- Numeracy1 Summer 2017 Coursework Brief
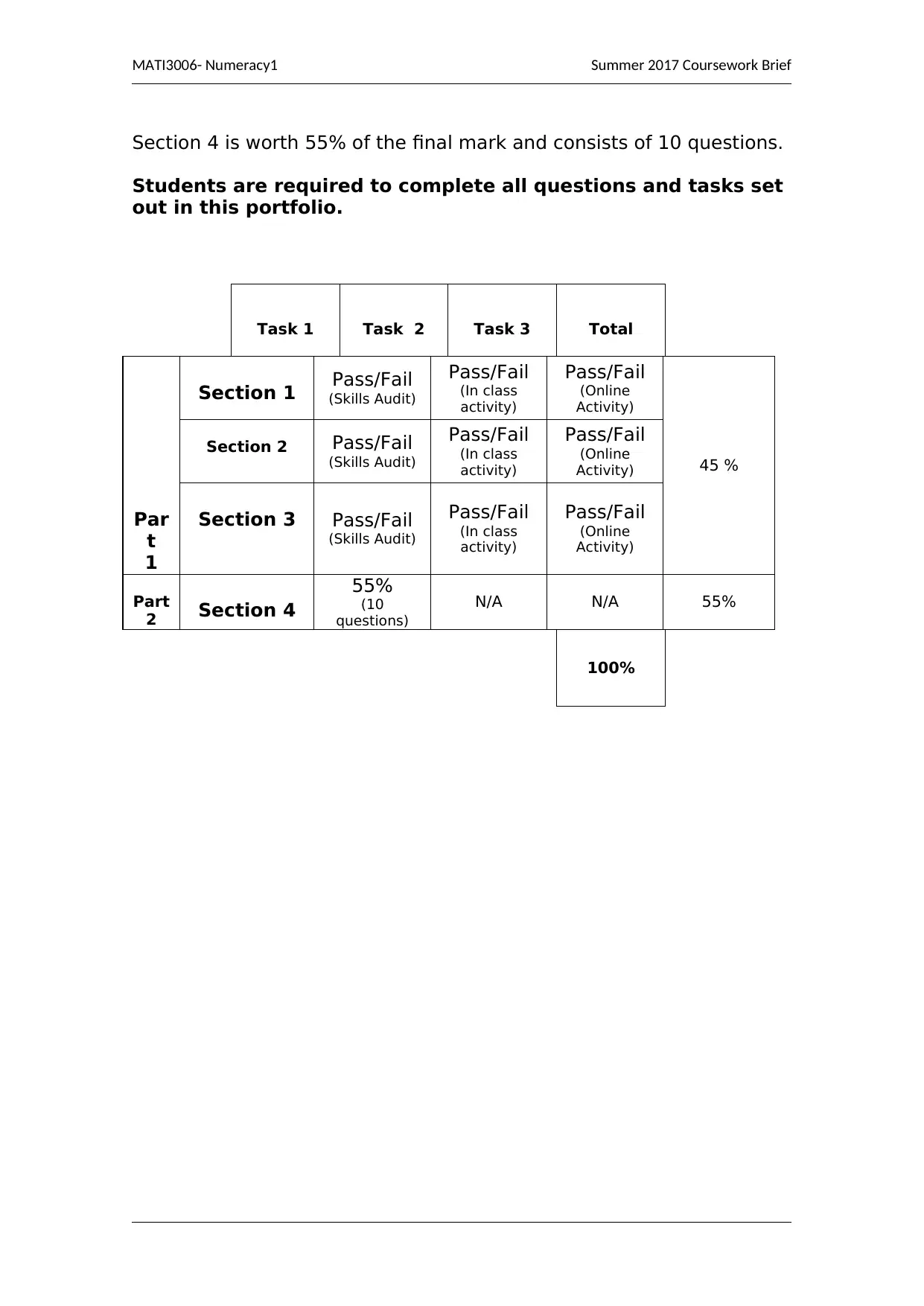
Section 4 is worth 55% of the final mark and consists of 10 questions.
Students are required to complete all questions and tasks set
out in this portfolio.
Task 1 Task 2 Task 3 Total
Par
t
1
Section 1 Pass/Fail
(Skills Audit)
Pass/Fail
(In class
activity)
Pass/Fail
(Online
Activity)
45 %
Section 2 Pass/Fail
(Skills Audit)
Pass/Fail
(In class
activity)
Pass/Fail
(Online
Activity)
Section 3 Pass/Fail
(Skills Audit)
Pass/Fail
(In class
activity)
Pass/Fail
(Online
Activity)
Part
2 Section 4
55%
(10
questions)
N/A N/A 55%
100%

MATI3006- Numeracy1 Summer 2017 Coursework Brief

MATI3006- Numeracy1 Summer 2017 Coursework Brief
Blank

MATI3006- Numeracy1 Summer 2017 Coursework Brief
SECTION 1
This section will focus on order of operations (BODMAS); operations on
positive and negative numbers; fractions and ratios.
Task 1: Skills Audit
Tick the appropriate column for each skill in the list below.
Please note that there is no right or wrong answer. Your
answers should show good reflection and awareness of your
strengths and areas for improvement.
I know how to…. I can
do well
I need
practic
e
I’m not
sure
I can’t
do
1. I know what BODMAS stands for. ☐ ☐ ☐ ☐
2. I can apply BODMAS to a variety of
calculations.
☐ ☐ ☐ ☐
3. I can define a fraction, numerator
and denominator.
☐ ☐ ☐ ☐
4. I can define proper fraction,
improper fraction and a mixed
number.
☐ ☐ ☐ ☐
5. I can convert a mixed number to
an improper fraction.
☐ ☐ ☐ ☐
6. I can convert improper fraction to a
mixed number.
☐ ☐ ☐ ☐
7. I can add, subtract, multiply and
divide fractions.
☐ ☐ ☐ ☐
8. I can explain the meaning of a
ratio.
☐ ☐ ☐ ☐
9. I can work with simple ratios. ☐ ☐ ☐ ☐
Task 2: In class Activity
QUESTION 1
Reflection
Write a short reflection (approximately 100-150 words) about your personal
learning experience of the topics covered in this section.
You can use the Skills Audit above to facilitate your answer. You may also
consider the following points:
 Reflect on your learning
 How did you contribute in the class?
 What went well?
 Are there any areas for improvement?

MATI3006- Numeracy1 Summer 2017 Coursework Brief
I have learnt the about how operators can be operated. This can be
done by using BODMAS method. I also understood clearly different
operations on positive and negative numbers. Like addition of positive
number with positive number, addition of positive to negative
number, etc. I also what is the definition of fractions and ratios and
their use in practical life also.
QUESTION 2
Give one example of a ‘real-life’ problem or situation that involves one (or
more) of the following topics:
 Order of operations
 Operations on positive and negative numbers
 Fractions
 Ratios
Also, please find a solution to the problem you described.
Order of operations (BODMAS)
Order of operations can be defined as the methods through which
mathematical calculation are done. BODMAS stands for Brackets, Order,
Division, Multiplication, Addition, Subtraction. Any of the mathematical sum
is solved according to the priorities of the operations that is discussed
below:
 Brackets > Of > Division > Multiplication > Addition > Subtraction
For example, problems like 7 + (5^2 * 6 + 3) is solved as following:
Brackets is solved first as follow:
Brackets is solved first as follow:
 First step: 6 * (5 + 3) = 6 * 8 = 48 (Correct)
 6 * (5 + 3) = 30 + 3 = 33 (wrong)
Then exponents ( power , roots) is solved before multiply, divide, add or subtract.
 Second step: 5 * 2^2= 5 * 4 = 20 (correct)
 5 * 2^2 =10^2 = 100 (wrong)
Then multiplication or division is performed before addition or subtraction
 Third step: 2+ 5 * 3 = 2 + 15 = 17 (correct)
 2 + 5 * 3 = 7 * 3 = 21 (wrong)
Otherwise just going left to right
 Fourth step : 30 / 5 + 3 = 6 * 3 = 18 (correct)
 30 / 5 * 3 = 30 / 15 = 2 (wrong)
Note: Order can be followed as :
B brackets first
O Orders (power and square roots)

MATI3006- Numeracy1 Summer 2017 Coursework Brief
DM Division and Multiplication (Left to right)
AS Addition and Subtraction (left to right)
Operations on positive and negative numbers
There are four operations that are applicable on positive and negative
numbers. This is explained below:
1. Additive rules:
 Addition of two positive numbers results in a positive number. For
example: 3+ 4 = 7.
 Addition of two negative number results in a negative number. For
example : (-6) + (-5) = -11.
 when a negative number is added with a positive number then sign of
greater number is taken and subtraction is performed here. For
example: (-8) + 5 = -3.
2. Subtracting rules:
 Negative - positive = Negative. e.g. (-6) - (-4) = -6 + 4 = -10.
 Positive - Negative = Positive + Positive = Positive. e.g. 5- (-5)
= 5 + 5 = 10.
 Negative - Negative = Negative + Positive = Here sign of larger
number is taken and subtraction is performed. e.g. (-5) - (-7) =
(-5) + 7 = -2; (-4) - (-6) = (-4) + 6 = 2, etc.
3. Multiplying rules:
 Positive * Positive = Positive. e.g. 45* 5= 25.
 Negative * Negative = Negative. e.g. (-6) * (-2) = -12.
 Negative * Positive = Negative. e.g. (-5) * 3 = -15.
 Positive * Negative = Negative. e.g. 3 * (-6) = -18.
4. Dividing rules:
 Positive / Positive = Positive. e.g. 21 / 7 = 3.
 Negative / Negative = Positive. e.g. (-14) / (-2) = 7.
 Negative / Positive = Negative. e.g. (-24) / 8 = -3.
 Positive / Negative = Negative. e.g. 16 / (-4) = -4.
Fractions : A mathematical expression showing the division of two whole
numbers are known as fractions. It is commonly used to indicate a part of
the whole number or a ratio between two numbers. Example of real life:
Suppose Ram has only one guava so he has to share with her sister. Then

MATI3006- Numeracy1 Summer 2017 Coursework Brief
he will cut that guava into two equal parts and give half ( ½) of this to her
sister.
Ratios: In mathematics, ratio shows the relationship between two numerals
denoting how many times the first number contains the other number. Real
life example of ratio: If a bowl of fruits contains four apples and five
mangoes, then the ratio of apple to mangoes will be written as 4 : 5.
Task 3: Online Activity
Evidence (screenshot) of completing and passing relevant online
quiz/activity.
Instruction:
1. Complete your online quiz/activity, (GSM Learn).
2. Take a screenshot.
3. Copy and paste the screenshot here..
SECTION 2
This section will focus on decimals, percentages and index numbers.

MATI3006- Numeracy1 Summer 2017 Coursework Brief
Task 1: Skills Audit
Tick the appropriate column for each skill in the list below.
Please note that there is no right or wrong answer. Your
answers should show good reflection and awareness of your
strengths and areas for improvement.
I know how to…. I can
do well
I need
practic
e
I’m not
sure
I can’t
do
10.I can describe the relationship
between fractions, decimals and
percentages.
☐ ☐ ☐ ☐
11.I can identify the decimal
equivalent of a percent.
☐ ☐ ☐ ☐
12.I can identify the fractional
equivalent of a percent.
☐ ☐ ☐ ☐
13.I can determine which concepts
and procedures are needed to
complete each practice exercise.
☐ ☐ ☐ ☐
14.I can compute answers by applying
appropriate formulas and
procedures.
☐ ☐ ☐ ☐
15.I can construct a simple index. ☐ ☐ ☐ ☐
16.I can interpret indexes to identify
trends in a data set.
☐ ☐ ☐ ☐
Task 2: In class Activity
QUESTION 1

MATI3006- Numeracy1 Summer 2017 Coursework Brief
Reflection
Write a short reflection (approximately 100-150 words) about your personal
learning experience of the topics covered in this section.
You can use the Skills Audit above to facilitate your answer. You may also
consider the following points:
 Reflect on your learning
 How did you contribute in the class?
 What went well?
 Are there any areas for improvement?
QUESTION 2
Give one example of a ‘real-life’ problem or situation that involves one (or
more) of the following topics:
 Decimals
 Percentages
 Index numbers
Also, please find a solution to the problem you described.
Decimals: A decimal is any number in the base ten system of
maths. Decimal point is used to denote isolation of once place from
the tenths place in decimal. Example : 46.89, 47. 35, etc.
Percentage: In maths, percentage is a number or ratio that is stated
as a fraction of 100. Its sign is %. Real life example: If 40 % of the
total number of students in a class is girl. This shows that 40 out of all
100 students are girls.
Index number: This is defined as a number that show how many
times the number is used in multiplication. This is also known as
power. Example: 3^2 * 4 = 9 * 4= 36.
Task 3: Online Activity
Evidence (screenshot) of completing and passing relevant online
quiz/activity
Instruction:
4. Complete your online quiz/activity, (GSM Learn).
5. Take a screenshot.
6. Copy and paste the screenshot here.

MATI3006- Numeracy1 Summer 2017 Coursework Brief
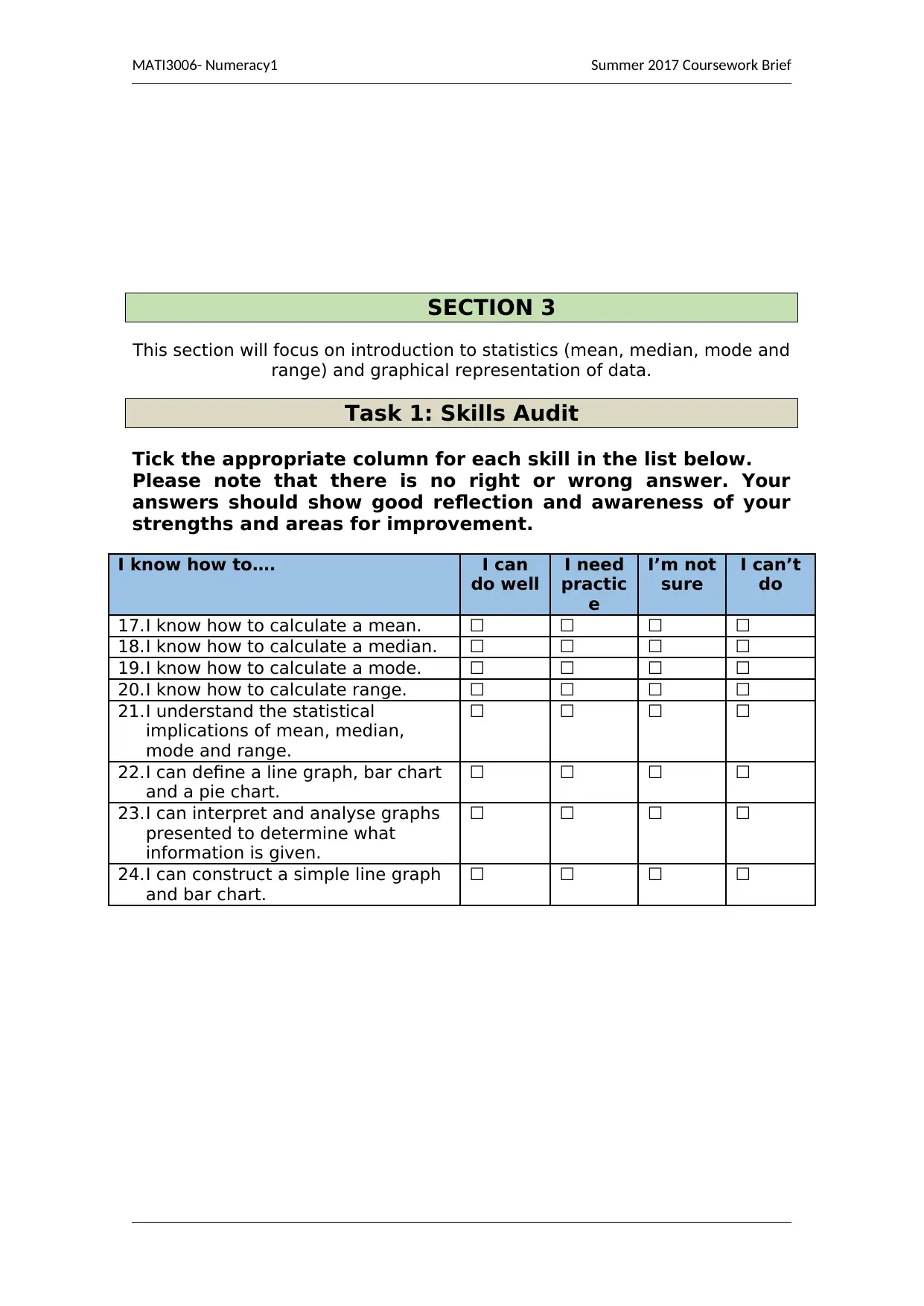
SECTION 3
This section will focus on introduction to statistics (mean, median, mode and
range) and graphical representation of data.
Task 1: Skills Audit
Tick the appropriate column for each skill in the list below.
Please note that there is no right or wrong answer. Your
answers should show good reflection and awareness of your
strengths and areas for improvement.
I know how to…. I can
do well
I need
practic
e
I’m not
sure
I can’t
do
17.I know how to calculate a mean. ☐ ☐ ☐ ☐
18.I know how to calculate a median. ☐ ☐ ☐ ☐
19.I know how to calculate a mode. ☐ ☐ ☐ ☐
20.I know how to calculate range. ☐ ☐ ☐ ☐
21.I understand the statistical
implications of mean, median,
mode and range.
☐ ☐ ☐ ☐
22.I can define a line graph, bar chart
and a pie chart.
☐ ☐ ☐ ☐
23.I can interpret and analyse graphs
presented to determine what
information is given.
☐ ☐ ☐ ☐
24.I can construct a simple line graph
and bar chart.
☐ ☐ ☐ ☐