Statistics Assignment Solutions

This document contains solutions to various questions related to statistics, including probability, binomial distribution, and expected value. The solutions are provided in a step-by-step manner, making it easy for students to understand. The document also includes relevant screenshots and tables to support the solutions.

STATISTICS
STUDENT ID:
[Pick the date]

Question 1
a) Value of π = 0.8
b) Value of q = 1-0.8 =0.2
c) Value of n =12 which indicates the number of trials
d) The relevant screenshot is indicated as follows.
e) The relevant screenshot is indicated below.

Question 2
a) Value of p = 0.95
b) Value of q = 1-0.95 = 0.05
c) The relevant details have been fed into the binomial calculator.
d) The expected probability would be zero considering the high probability of the guests
turning up when reservation is made.
e) Yes, the answer also comes out as zero from the use of the binomial calculator.

f) The requisite number is N = 412.
Question 3
a) Requisite probability = (69-5)/69 = 64/69
b) The white balls are drawn without replacement, hence there are 63 non-winning white
balls in the bag and a total of 68 balls.
Requisite probability = 63/68
c) The white balls are drawn without replacement, hence there are 62 non-winning white
balls in the bag and a total of 67 balls.
Requisite probability = 62/67
d) The white balls are drawn without replacement, hence there are 61 non-winning white
balls in the bag and a total of 66 balls.
Requisite probability = 61/66
e) The white balls are drawn without replacement, hence there are 60 non-winning white
balls in the bag and a total of 65 balls.
Requisite probability = 60/65 = 12/13
f) Probability of picking the winning red ball from the other bag = (1/26)
g) Probability of winning the Power Ball lowest prize =
(64/69)*(63/68)*(62/67)*(61/66)*(60/65)*(1/26) = 1/38.32

Question 4
The requisite values based on the given data are indicated below.
AAAA = 0.55
BBBB- 0.45
CCCC = 0.2
DDDD = 0.8
EEEE = 0.75
FFFF = 0.25
GGGG = 0.55*0.2 = 0.11
HHHH = 0.55*0.8 = 0.44
IIII = 0.45*0.75 = 0.3375
JJJJ = 0.45*0.25 = 0.1125
a) P(Safe) = GGGG + IIII = 0.11+0.3375 = 0.4475
b) P(safe|curve ball) = EEEE = 0.75
c) P(curve ball| safe)= P(Curve ball & Safe) /P(Safe) = IIII/(GGGG+IIII) = 0.3375/0.4475 =
0.7542
Question 5
a) Requisite probability = 13C1*(4/52) = 1 as there are 13 possible options for X and hence 1
value of X ought to be selected.
b) Since, there is no replacement of cards, hence there are now three X in the deck and total
of 51 cards.

Requisite probability = (3/51) = (1/17) = 0.0588
c) Since, there is no replacement of cards, hence there are now 2 X in the deck and total of 50
cards.
Requisite probability = (2/50) = (1/25) = 0.04
d) Since, there is no replacement of cards, hence there are now 4Z in the deck and total of 49
cards. Further, 12 possible values of Z are possible out of which 1 needs to selected.
Requisite probability =12C1*(4/49) = (48/49) =0.9796
e) Since, there is no replacement of cards, hence there are now 3Z in the deck and total of 48
cards.
Requisite probability = (3/48) = (1/16) = 0.0625
f) The multiplication factor is F = 5 !
3!∗2 ! as multiple arrangements are possible which need to
be considered.
g) Final probability = (1)*(1/17)*(1/25)*(48/49)*(1/16)* 5 !
3!∗2 ! = (1/694.167)
Question 6
a) Value of area ‘3’ is 300 since these students have both maths and classics.
b) Value of area ‘2’ = 1000-300 = 700 since ‘2’ represents area which is only maths
c) Value of area ‘4’ = 800-300 = 500 since ‘4’ represents area which is only classics.
d) Value of area’1’ = Total students – Value of area ‘2’ - Value of area ‘3’ - Value of area ‘4’
= 2000 – 300-700-500 = 500
e) Value of area “2+3” = 700 + 300 = 1000
Hence, P(A) = 1000/2000 = 0.5
f) Value of area “3+4” = 300 + 500 = 800

Hence, P(B) = 800/2000 = 0.4
g) P(A ∩ B) = Value of area ‘3’/Total number of students = 300/2000 = 0.15
h) P(A U B) = P(A) + P(B) - P(A ∩ B) = 0.5 + 0.4 -0.15 = 0.75
i)No, A and B are not mutually exclusive as there are common elements which occur in both
A and B and are captured by area ‘3’
j) P(A)*P(B) = 0.5*0.4 = 0.2
Clearly, the above is not equal to P(A ∩ B) which has been computed as 0.15 and hence A
and B are not independent events.
k) P(A|B) = P(A∩B)/P(B) = 0.15/0.4 = 0.375
l) P(B|A) = P(B∩A)/P(A) = 0.15/0.5 = 0.3
Question 7
a) The relevant labelling of the box is indicated below.
Particulars 1(2nd roll) 2 3 4 5 6
1(1st roll)
2
3 A A A A A A
4
5
6 A A A A A A
b) The relevant labelling of the box is indicated below.
Particulars 1(2nd roll) 2 3 4 5 6
1(1st roll) B
2 B
3 A A AB A A A
4 B

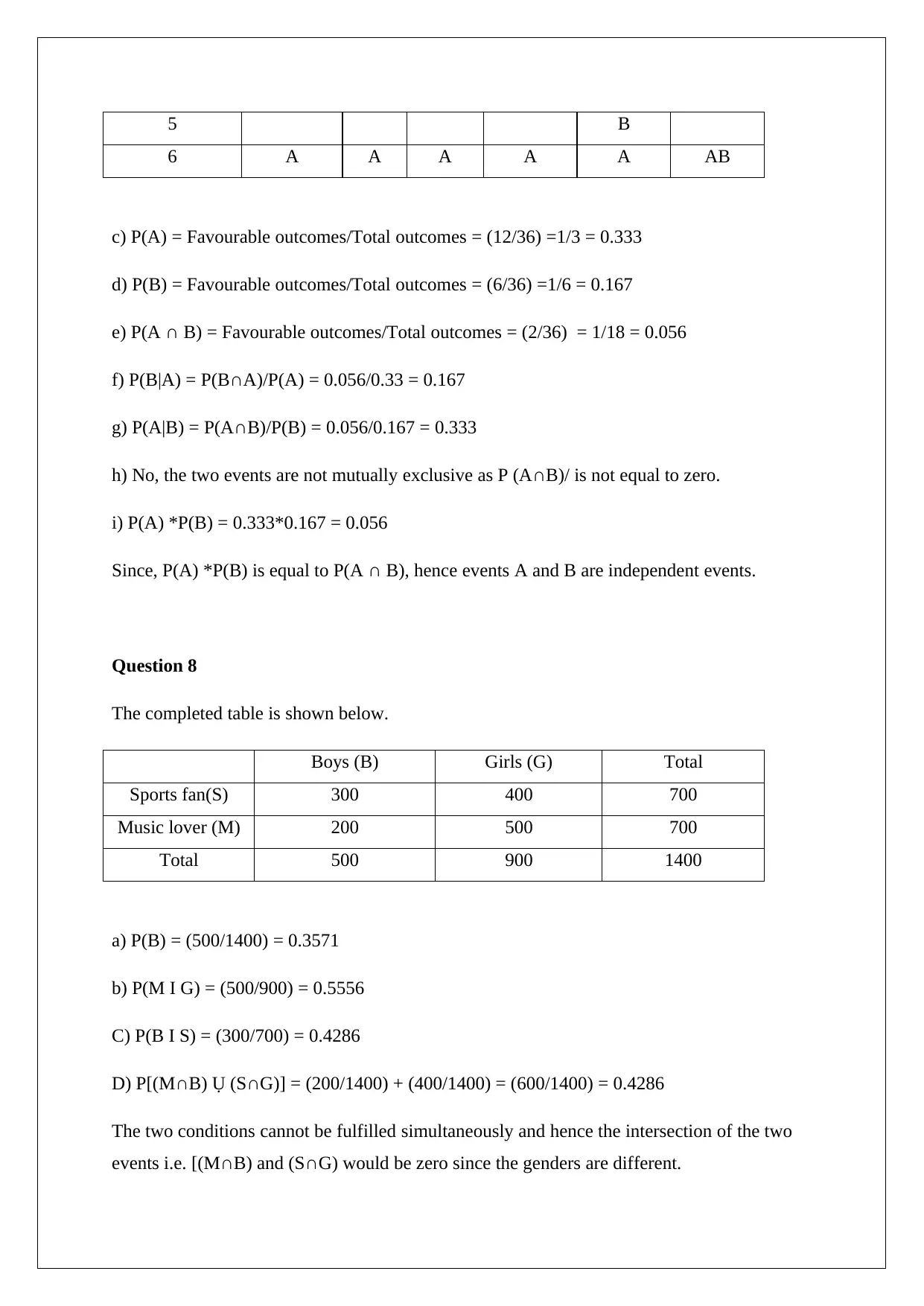
5 B
6 A A A A A AB
c) P(A) = Favourable outcomes/Total outcomes = (12/36) =1/3 = 0.333
d) P(B) = Favourable outcomes/Total outcomes = (6/36) =1/6 = 0.167
e) P(A ∩ B) = Favourable outcomes/Total outcomes = (2/36) = 1/18 = 0.056
f) P(B|A) = P(B∩A)/P(A) = 0.056/0.33 = 0.167
g) P(A|B) = P(A∩B)/P(B) = 0.056/0.167 = 0.333
h) No, the two events are not mutually exclusive as P (A∩B)/ is not equal to zero.
i) P(A) *P(B) = 0.333*0.167 = 0.056
Since, P(A) *P(B) is equal to P(A ∩ B), hence events A and B are independent events.
Question 8
The completed table is shown below.
Boys (B) Girls (G) Total
Sports fan(S) 300 400 700
Music lover (M) 200 500 700
Total 500 900 1400
a) P(B) = (500/1400) = 0.3571
b) P(M I G) = (500/900) = 0.5556
C) P(B I S) = (300/700) = 0.4286
D) P[(M∩B) Ụ (S∩G)] = (200/1400) + (400/1400) = (600/1400) = 0.4286
The two conditions cannot be fulfilled simultaneously and hence the intersection of the two
events i.e. [(M∩B) and (S∩G) would be zero since the genders are different.

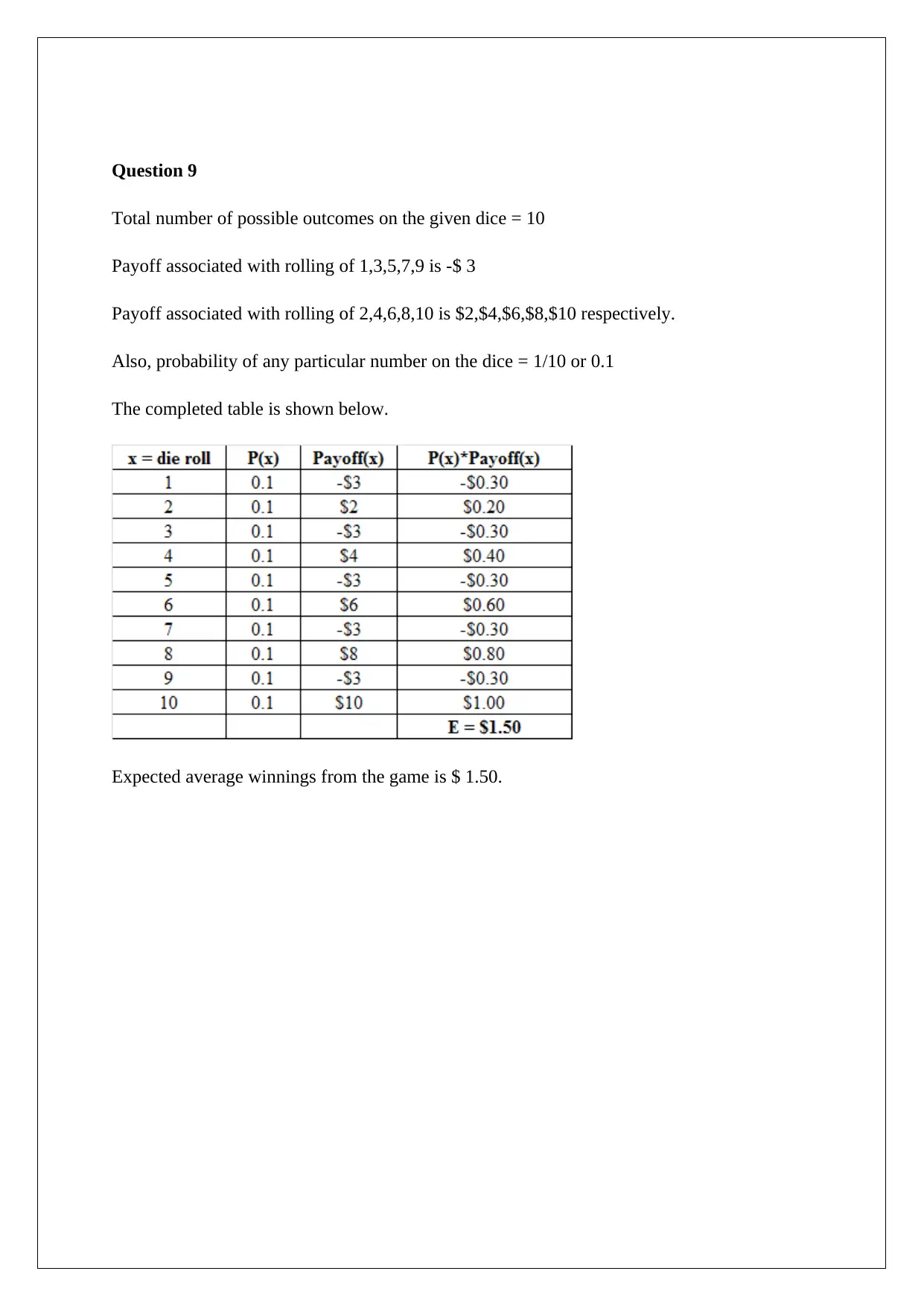
Question 9
Total number of possible outcomes on the given dice = 10
Payoff associated with rolling of 1,3,5,7,9 is -$ 3
Payoff associated with rolling of 2,4,6,8,10 is $2,$4,$6,$8,$10 respectively.
Also, probability of any particular number on the dice = 1/10 or 0.1
The completed table is shown below.
Expected average winnings from the game is $ 1.50.