Statistics for Business and Finance Assignment

This article discusses the results of data analysis for Statistics for Business and Finance Assignment. It covers topics such as computation of stock prices, hypothesis testing, CAPM model, and more. The analysis was done using Microsoft Excel and SPSS software.

Running Head: STATISTICS FOR BUSINESS AND FINANCE ASSIGNMENT
STATISTICS FOR BUSINESS AND FINANCE ASSIGNMENT
Student’s Name
Institution Affiliation

2 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
Contents
1. Computation of the return of the three series of stock prices...............................................................3
1.1. Jarque-Berra test: Are GD and Boeing Stocks’ Returns normally distributed or not?................3
1.2. Risk–return relationship...............................................................................................................4
2. Hypothesis test at 0.05% significant level: Is average returns of GD stock is equal to 2.8% or
different?.....................................................................................................................................................5
3. Hypothesis test at 0.05% significant level: Are the variances of GD and Boeing (BA) stocks similar
or different?.................................................................................................................................................5
4. Hypothesis test at 0.05% significant level: Are the average returns of GD and BA stocks equal or
not?..............................................................................................................................................................6
5. CAPM Model..........................................................................................................................................7
5.0. Computation of excess return of GD and excess market return........................................................7
5.1. CAPM Estimation.............................................................................................................................7
5.2. Interpretation of CAPM Beta............................................................................................................8
5.3. Interpretation of R 2.........................................................................................................................8
5.4. Interpretation of confidence interval for CAPM Beta.......................................................................8
6. Hypothesis test using confidence interval approach at 0.05% significant level: Is GD stock a neutral
stock or not?................................................................................................................................................8
7. Hypothesis test at 0.05% significant level: Is error term in ordinary least squares normally distributed
or not?.........................................................................................................................................................9
Reference...................................................................................................................................................10
APPENDIX...............................................................................................................................................10
Table 1: Computed Returns for GSPC, GD and BA stock prices..........................................................10
Table 2: Computed Excess Returns for GD...........................................................................................12

3 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
Data Analysis
The analysis and calculating were done in Microsoft Excel and SPSS software. Below are the
results of the results of data analysis as per the Task.
1. Computation of the return of the three series of stock prices
The following formula was used: rt=100∗ln(Pt / Pt−1)
The results of computation are presented in table 1 at the appendix shows
1.1. Jarque-Berra test: Are GD and Boeing Stocks’ Returns normally
distributed or not?
This test was partly done on SPSS.
The table is a summary of the results Skewness and Kurtosis for the Jarque-Berra test
Descriptive Statistics
N Mean Std.
Deviation
Skewness Kurtosis
Statistic Statistic Statistic Statistic Std.
Error
Statistic Std.
Error
GD 60 1.77685 4.497032 .221 .309 .370 .608
BA 60 1.66947 5.927002 -.628 .309 1.277 .608
Valid N
(listwise) 60
Form the Skewness and Kurtosis the Jarque-Berra test will be given by
JB=n { S2
6 + K2
24 }, where S=skewness∧K =kurtosis , n=sample

4 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
GD Stock
JB=60 { ( 0.221 )2
6 + ( 0.37 )2
24 }=0.83
Boeing Stock (BA)
JB=60 { (−0.628)2
6 + (1.277)2
24 }=0.1285
The two JB obtained were compared with the critical value of Chi-Square χα =0.05∧df =2
2 =9.192.
Since the JB for the GD and Boeing Stocks are less than the critical value, the null hypothesis
that the returns of GD and Boeing are normally distributed will be accepted. This suggests that
the return of the G and Boeing are normally distributed.
1.2. Risk–return relationship
According to Bhat (2009), in finance risk is measured using the standard deviation of returns of
assets. He urges that the high standard deviation indicates high level risk whereas a small
standard deviation indicates low risk level. From the table in 1.1 above standard deviation of GD
and Boeing stocks are 4.5 and 5.9 respectively. Since the standard deviation of Boeing is higher
than that of GD, its returns are said to be associated with a high level of risk compared to that of
GD stock. This suggests that GD stock is a better investment than Boeing stock.

5 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
2. Hypothesis test at 0.05% significant level: Is average returns of GD
stock is equal to 2.8% or different?
The test statistic used to perform the test is z-statistic as the sample size of GD is greater than 30
(Francis, 2004). This test was performed in SPPS software. Results are presented in the table
below. From the table, P-value of the test is 0.083, which is greater than 0.05 significant level.
This implies that null hypothesis ( H0=2.8) will be adopted as large P- values indicates that data
supports the null hypothesis (Ruppert, 2014). This reveals that that the average returns of GD
is not significantly different from 2.8% at 0.05 significant level.
One-Sample Test
Test Value = 2.8
t df Sig. (2-
tailed)
Mean
Difference
95% Confidence Interval
of the Difference
Lower Upper
GD -1.762 59 .083 -1.023209 -2.18493 .13851
3. Hypothesis test at 0.05% significant level: Are the variances of GD and
Boeing (BA) stocks similar or different?
The F- statistic was used to perform the test. This test was performed in Microsoft Excel software.
The results are shown in the table below.
The P- value of
the test is 0.0179,
which is less than
0.05 significant levels. This implies that there’s a significant difference between the variance
F-Test Two-Sample for Variances
GD BA
Mean 1.77679051 1.669380116
Variance 20.223707 35.12921694
Observations 60 60
df 59 59
F 0.57569478
P(F<=f) one-tail 0.01792698
F Critical one-tail 0.64936895

6 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
returns of GD and BA stock, which has been revealed by respective variances of the 20.22 and
96.47. High variance value an indicator of high risk while variance indicates low risks (Ehrhardt
& Brigham 2016). This implies that the returns of GD are associated with low risks due to
smaller variance whereas returns will be associated with higher risks.
4. Hypothesis test at 0.05% significant level: Are the average returns of
GD and BA stocks equal or not?
The ANOVA test was conducted using Microsoft excel, to determine whether there is difference
between the average returns of GD and Boeing Stock. The results are present in the below.
Anova: Single
Factor
SUMMARY
Groups Count Sum Average Variance
GD 60 106.6074 1.7768 20.2237
BA 60 100.1628 1.6694 35.1292
ANOVA
Source of Variation SS df MS F P-value F crit
Between Groups 0.34611 1 0.3461 0.0125 0.9111 3.9215
Within Groups
3265.822
5 118 27.6765
Total 3266.169 119
The P-value of the test is 0.911, which is greater than 0.05 significant level, therefore null
hypothesis will be accepted . This implies that there is no significant difference between the
average returns of GD and BA stocks at 0.05 significant levels.

7 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
5. CAPM Model
5.0. Computation of excess return of GD and excess market return.
The excess market return of GD was computed by the formula: yt=rt−rf ,t and excess market
return by XM =rM , t−rf , t on Microsoft Excel. The results are presented in table 2 at the
appendix.
5.1. CAPM Estimation
The of regression analysis of excess return of GD ( yt) stock on excess return market ( X M) was
performed in Microsoft Excel. The result presented in the table below. From the result below,
CAPM estimate will be given by the equation: yt =0.55+0.71 X M
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.4689
R Square 0.2199
Adjusted R
Square 0.2065
Standard
Error 3.9351
Observation
s 60
ANOVA
df SS MS F
Significa
nce F
Regression 1 253.177
253.17
661
16.35
004 0.00016
Residual 58 898.117
15.484
8
Total 59 1151.293
Coeffic
ients
Standard
Error t Stat
P-
value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 0.5499 0.5541 0.9924
0.325
1 -0.5592 1.6590 -0.5592 1.6590
Xm 0.7104 0.1757 4.0435 0.002 0.3587 1.0620 0.3587 1.0620

8 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
5.2. Interpretation of CAPM Beta
The CAPM Beta is given by the coefficient of excess market return (X M ), 0.71. This beta is less
than, indicating that the price of GD stock is less volatile than the market price (Feibel 2003).
This is an indicator of minimal risks associated with GD returns.
5.3. Interpretation of R2
The value of R2 is 0.2199%. R2 measures the variation of between the variable data and the
fitted values, R2 closer to 100% indicates that the model explains all the variations between
them (Jackson, 2013 ) . Since 0.2199 % is not close to 100% all the variations of excess return
of GD stock are not well fitted by the regression model.
5.4. Interpretation of confidence interval for CAPM Beta
From the table above the 95% confidence interval of CAPM Beta is (0.3587, 1.062). This
indicates that the volatility of the price of GD in the stock markets ranges between 0.3587 and
1.062
6. Hypothesis test using confidence interval approach at 0.05%
significant level: Is GD stock a neutral stock or not?
According to Barmish& Primbs (2012), the stock is said to be neutral if the associate beta value
is equal to 1. The test was conducted using regression analysis in SPSS, for the excess return of
GD on excess market returns. The following table represents the analytical result.
Coefficients a
Model 95.0% Confidence Interval for B
Lower Bound Upper Bound
1 (Constant) -.559 1.659
Xm .359 1.062

9 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
From the table above the confidence interval of the beta, the coefficient is (0.359, 1.062). Since
1 is within the confidence interval, then the null hypothesis that the stock GD is a neutral stock
will be adopted. This clearly reveals that GD stock is neutral stock.
7. Hypothesis test at 0.05% significant level: Is error term in ordinary
least squares normally distributed or not?
The least square model yt =0.55+0.71 X M was used to obtain the Predicted values of excess
returns ( yt), which was then utilized in computing the unstandardized residual values together
with observed values of( y ¿¿ t) ¿. Kolmogorov-Smirnov and Shapiro-Wilk tests were later
performed using SPSS software to determine the normality of the residual and results are
presented in the table below.
Tests of Normality
Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
Unstandardized Residual .087 60 .972 60 .174
The P-values Kolmogorov-Smirnov and Shapiro-Wilk tests of are greater than 0.05 significant
levels. This implies that the null hypothesis will be adopted and therefore, the assumption of
normally distributed error in ordinary least squares is plausible.

10 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
Reference
Bhat, S., 2009. Security Analysis & Portfolio Management. Excel Books India.
Barmish, B.R. and Primbs, J.A., 2012, June. On market-neutral stock trading arbitrage via linear
feedback. In American Control Conference (ACC), 2012 (pp. 3693-3698). IEEE.
Ehrhardt, M.C., and Brigham, E.F., 2016. Corporate finance: A focused approach. Cengage
Learning.
Francis, A., 2004. Business mathematics and statistics. Cengage Learning EMEA.
Feibel, B.J., 2003. Investment performance measurement(Vol. 116). John Wiley & Sons.
Jackson, S.L., 2013. Statistics plain and simple. Cengage Learning.
Ruppert, D. 2014. Statistics and finance: an introduction. Springer.
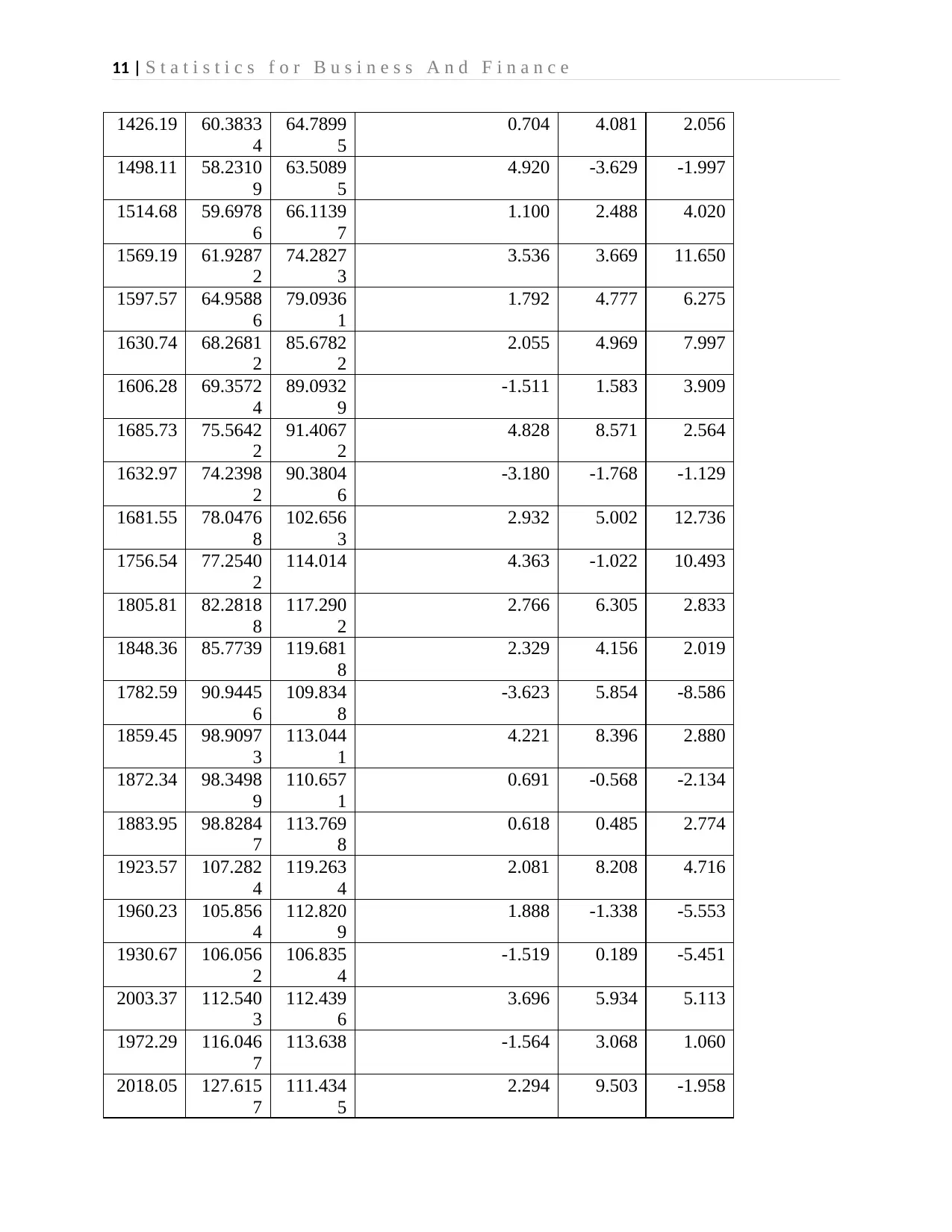
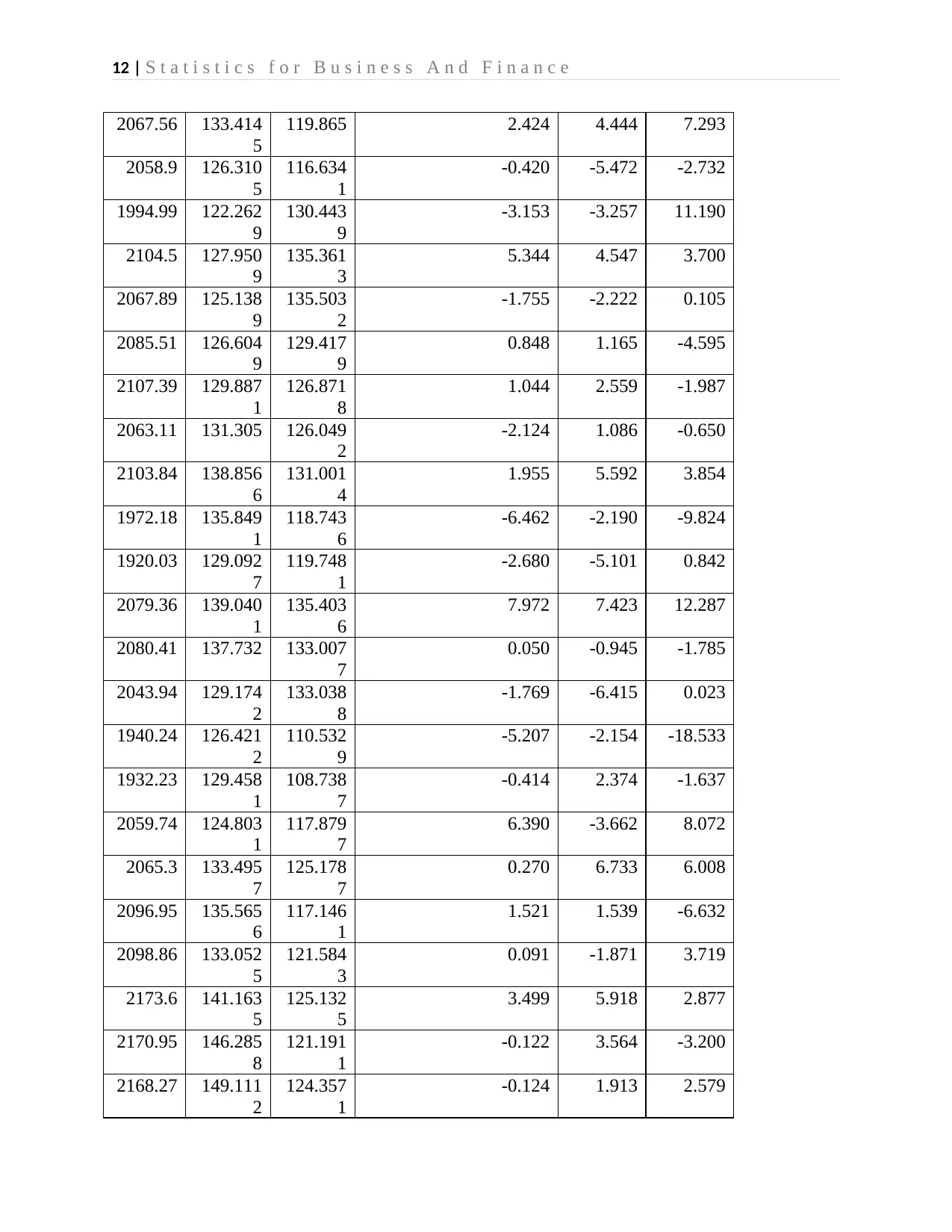
APPENDIX
Table 1: Computed Returns for GSPC, GD and BA stock prices
GSPC GD BA Returns= 100*LN(Pt/Pt-1)
1408.47 62.5288
7
62.8007
4
GSPC GD BA
1397.91 57.5183
8
64.8527
3
-0.753 -8.352 3.215
1310.33 54.9478 58.7812
2
-6.470 -4.572 -9.830
1362.16 56.6217
2
63.1099
1
3.879 3.001 7.106
1379.32 54.4584
9
62.7786
6
1.252 -3.895 -0.526
1406.58 56.6729
6
60.6466
6
1.957 3.986 -3.455
1440.67 57.2006
9
59.4722
8
2.395 0.927 -1.955
1412.16 58.8962
8
60.1900
7
-1.999 2.921 1.200
1416.18 57.9687 63.4712
8
0.284 -1.587 5.308

11 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
1426.19 60.3833
4
64.7899
5
0.704 4.081 2.056
1498.11 58.2310
9
63.5089
5
4.920 -3.629 -1.997
1514.68 59.6978
6
66.1139
7
1.100 2.488 4.020
1569.19 61.9287
2
74.2827
3
3.536 3.669 11.650
1597.57 64.9588
6
79.0936
1
1.792 4.777 6.275
1630.74 68.2681
2
85.6782
2
2.055 4.969 7.997
1606.28 69.3572
4
89.0932
9
-1.511 1.583 3.909
1685.73 75.5642
2
91.4067
2
4.828 8.571 2.564
1632.97 74.2398
2
90.3804
6
-3.180 -1.768 -1.129
1681.55 78.0476
8
102.656
3
2.932 5.002 12.736
1756.54 77.2540
2
114.014 4.363 -1.022 10.493
1805.81 82.2818
8
117.290
2
2.766 6.305 2.833
1848.36 85.7739 119.681
8
2.329 4.156 2.019
1782.59 90.9445
6
109.834
8
-3.623 5.854 -8.586
1859.45 98.9097
3
113.044
1
4.221 8.396 2.880
1872.34 98.3498
9
110.657
1
0.691 -0.568 -2.134
1883.95 98.8284
7
113.769
8
0.618 0.485 2.774
1923.57 107.282
4
119.263
4
2.081 8.208 4.716
1960.23 105.856
4
112.820
9
1.888 -1.338 -5.553
1930.67 106.056
2
106.835
4
-1.519 0.189 -5.451
2003.37 112.540
3
112.439
6
3.696 5.934 5.113
1972.29 116.046
7
113.638 -1.564 3.068 1.060
2018.05 127.615
7
111.434
5
2.294 9.503 -1.958

12 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
2067.56 133.414
5
119.865 2.424 4.444 7.293
2058.9 126.310
5
116.634
1
-0.420 -5.472 -2.732
1994.99 122.262
9
130.443
9
-3.153 -3.257 11.190
2104.5 127.950
9
135.361
3
5.344 4.547 3.700
2067.89 125.138
9
135.503
2
-1.755 -2.222 0.105
2085.51 126.604
9
129.417
9
0.848 1.165 -4.595
2107.39 129.887
1
126.871
8
1.044 2.559 -1.987
2063.11 131.305 126.049
2
-2.124 1.086 -0.650
2103.84 138.856
6
131.001
4
1.955 5.592 3.854
1972.18 135.849
1
118.743
6
-6.462 -2.190 -9.824
1920.03 129.092
7
119.748
1
-2.680 -5.101 0.842
2079.36 139.040
1
135.403
6
7.972 7.423 12.287
2080.41 137.732 133.007
7
0.050 -0.945 -1.785
2043.94 129.174
2
133.038
8
-1.769 -6.415 0.023
1940.24 126.421
2
110.532
9
-5.207 -2.154 -18.533
1932.23 129.458
1
108.738
7
-0.414 2.374 -1.637
2059.74 124.803
1
117.879
7
6.390 -3.662 8.072
2065.3 133.495
7
125.178
7
0.270 6.733 6.008
2096.95 135.565
6
117.146
1
1.521 1.539 -6.632
2098.86 133.052
5
121.584
3
0.091 -1.871 3.719
2173.6 141.163
5
125.132
5
3.499 5.918 2.877
2170.95 146.285
8
121.191
1
-0.122 3.564 -3.200
2168.27 149.111
2
124.357
1
-0.124 1.913 2.579

13 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
2126.15 144.863
4
134.448 -1.962 -2.890 7.802
2198.81 169.352
3
142.122
3
3.360 15.619 5.551
2238.83 169.390
9
149.227
8
1.804 0.023 4.879
2278.87 174.886
3
156.647 1.773 3.193 4.852
2363.64 184.112
8
172.760
3
3.652 5.141 9.791
2362.72 181.581
2
170.988
3
-0.039 -1.385 -1.031
Average 0.862 1.777 1.669
Varianc
e
8.556 20.224 35.129
Standard Deviation 2.925 4.497 5.927
Table 2: Computed Excess Returns for GD
rm rt rf
Excess Return of
GD
Excess Market
Return
GSPC GD TNX Yt= rt- rf Xm= rm- rf
-0.753 -8.352 1.915 -10.267 -2.668
-6.470 -4.572 1.581 -6.153 -8.051
3.879 3.001 1.659 1.342 2.220
1.252 -3.895 1.492 -5.387 -0.240
1.957 3.986 1.562 2.424 0.395
2.395 0.927 1.637 -0.710 0.758
-1.999 2.921 1.686 1.235 -3.685
0.284 -1.587 1.606 -3.193 -1.322
0.704 4.081 1.756 2.325 -1.052
4.920 -3.629 1.985 -5.614 2.935
1.100 2.488 1.888 0.600 -0.788
3.536 3.669 1.852 1.817 1.684
1.792 4.777 1.675 3.102 0.117
2.055 4.969 2.164 2.805 -0.109
-1.511 1.583 2.478 -0.895 -3.989
4.828 8.571 2.593 5.978 2.235
-3.180 -1.768 2.749 -4.517 -5.929
2.932 5.002 2.615 2.387 0.317
4.363 -1.022 2.542 -3.564 1.821
2.766 6.305 2.741 3.564 0.025

14 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e
2.329 4.156 3.026 1.130 -0.697
-3.623 5.854 2.668 3.186 -6.291
4.221 8.396 2.658 5.738 1.563
0.691 -0.568 2.723 -3.291 -2.032
0.618 0.485 2.648 -2.163 -2.030
2.081 8.208 2.457 5.751 -0.376
1.888 -1.338 2.516 -3.854 -0.628
-1.519 0.189 2.556 -2.367 -4.075
3.696 5.934 2.343 3.591 1.353
-1.564 3.068 2.508 0.560 -4.072
2.294 9.503 2.335 7.168 -0.041
2.424 4.444 2.194 2.250 0.230
-0.420 -5.472 2.17 -7.642 -2.590
-3.153 -3.257 1.675 -4.932 -4.828
5.344 4.547 2.002 2.545 3.342
-1.755 -2.222 1.934 -4.156 -3.689
0.848 1.165 2.046 -0.881 -1.198
1.044 2.559 2.095 0.464 -1.051
-2.124 1.086 2.335 -1.249 -4.459
1.955 5.592 2.205 3.387 -0.250
-6.462 -2.190 2.2 -4.390 -8.662
-2.680 -5.101 2.06 -7.161 -4.740
7.972 7.423 2.151 5.272 5.821
0.050 -0.945 2.218 -3.163 -2.168
-1.769 -6.415 2.269 -8.684 -4.038
-5.207 -2.154 1.931 -4.085 -7.138
-0.414 2.374 1.74 0.634 -2.154
6.390 -3.662 1.786 -5.448 4.604
0.270 6.733 1.819 4.914 -1.549
1.521 1.539 1.834 -0.295 -0.313
0.091 -1.871 1.488 -3.359 -1.397
3.499 5.918 1.458 4.460 2.041
-0.122 3.564 1.568 1.996 -1.690
-0.124 1.913 1.608 0.305 -1.732
-1.962 -2.890 1.834 -4.724 -3.796
3.360 15.619 2.368 13.251 0.992
1.804 0.023 2.479 -2.456 -0.675
1.773 3.193 2.451 0.742 -0.678
3.652 5.141 2.358 2.783 1.294
-0.039 -1.385 2.396 -3.781 -2.435

15 | S t a t i s t i c s f o r B u s i n e s s A n d F i n a n c e