Report: Statistics for Financial Decision Making Analysis
VerifiedAdded on 2021/01/02
|12
|2652
|122
Report
AI Summary
This report delves into the application of statistical tools, particularly regression analysis, in financial decision-making. It begins with an introduction to statistics and its importance in business, followed by an examination of a regression model involving market price as the dependent variable and several independent variables, including Sydney price index, annual percentage change, total number of square meters, and age of the house. The report presents the full model, the least squares regression equation, and interprets the coefficients, discussing their significance. The coefficient of determination is evaluated to assess the model's goodness of fit. Confidence intervals for each parameter are stated, and hypothesis testing is conducted to determine the significance of each independent variable. Finally, the original and re-estimated models are compared, and the market price of a house with 400 square meters is predicted. The report concludes by summarizing the findings and providing references.

STATISTICS FOR FINANCIAL
DECISION
DECISION
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

TABLE OF CONTENTS
INTRODUCTION...........................................................................................................................1
TASK 1............................................................................................................................................1
TASK 2............................................................................................................................................2
TASK 3............................................................................................................................................4
Presenting full model..................................................................................................................4
TASK 4............................................................................................................................................5
Least squares regression equation and interpreting the equation................................................5
TASK 5............................................................................................................................................5
Interpreting estimated coefficients of regression model with discussion of significance values
.....................................................................................................................................................5
TASK 6............................................................................................................................................7
Value of coefficient of determination for relationship among dependent and independent
variables......................................................................................................................................7
TASK 7............................................................................................................................................7
Stating 95% confidence interval for every parameter.................................................................7
TASK 8............................................................................................................................................8
TASK 9............................................................................................................................................8
Comparing original and re-estimated model...............................................................................8
TASK 10..........................................................................................................................................9
Predicting market price of house with 400 square meters..........................................................9
CONCLUSION................................................................................................................................9
REFERENCES..............................................................................................................................10
INTRODUCTION...........................................................................................................................1
TASK 1............................................................................................................................................1
TASK 2............................................................................................................................................2
TASK 3............................................................................................................................................4
Presenting full model..................................................................................................................4
TASK 4............................................................................................................................................5
Least squares regression equation and interpreting the equation................................................5
TASK 5............................................................................................................................................5
Interpreting estimated coefficients of regression model with discussion of significance values
.....................................................................................................................................................5
TASK 6............................................................................................................................................7
Value of coefficient of determination for relationship among dependent and independent
variables......................................................................................................................................7
TASK 7............................................................................................................................................7
Stating 95% confidence interval for every parameter.................................................................7
TASK 8............................................................................................................................................8
TASK 9............................................................................................................................................8
Comparing original and re-estimated model...............................................................................8
TASK 10..........................................................................................................................................9
Predicting market price of house with 400 square meters..........................................................9
CONCLUSION................................................................................................................................9
REFERENCES..............................................................................................................................10
INTRODUCTION
The term statistics is concerned with the process of numerical and data analysis of the
given data set values. By making correct and proper analysis, interpretation of the given data set,
sound and effective business and financial decision can be made for the betterment of business
operations. The present report is based on regression analysis, which is considered as one of the
most important statistical business tool. With the help of this statistical tool, relationship between
two variables can be studied. Influence of one or more independent variables on a dependent
variable can be examined. The report will contain plotting of dependent variable against
independent variable by using scatter plot or dot function and relationship from this plotting. It
will disclose concept of the least square regression equation along with interpretation. At last,
comparison and evaluation of goodness of fit between the original model and re estimated model
will be made.
TASK 1
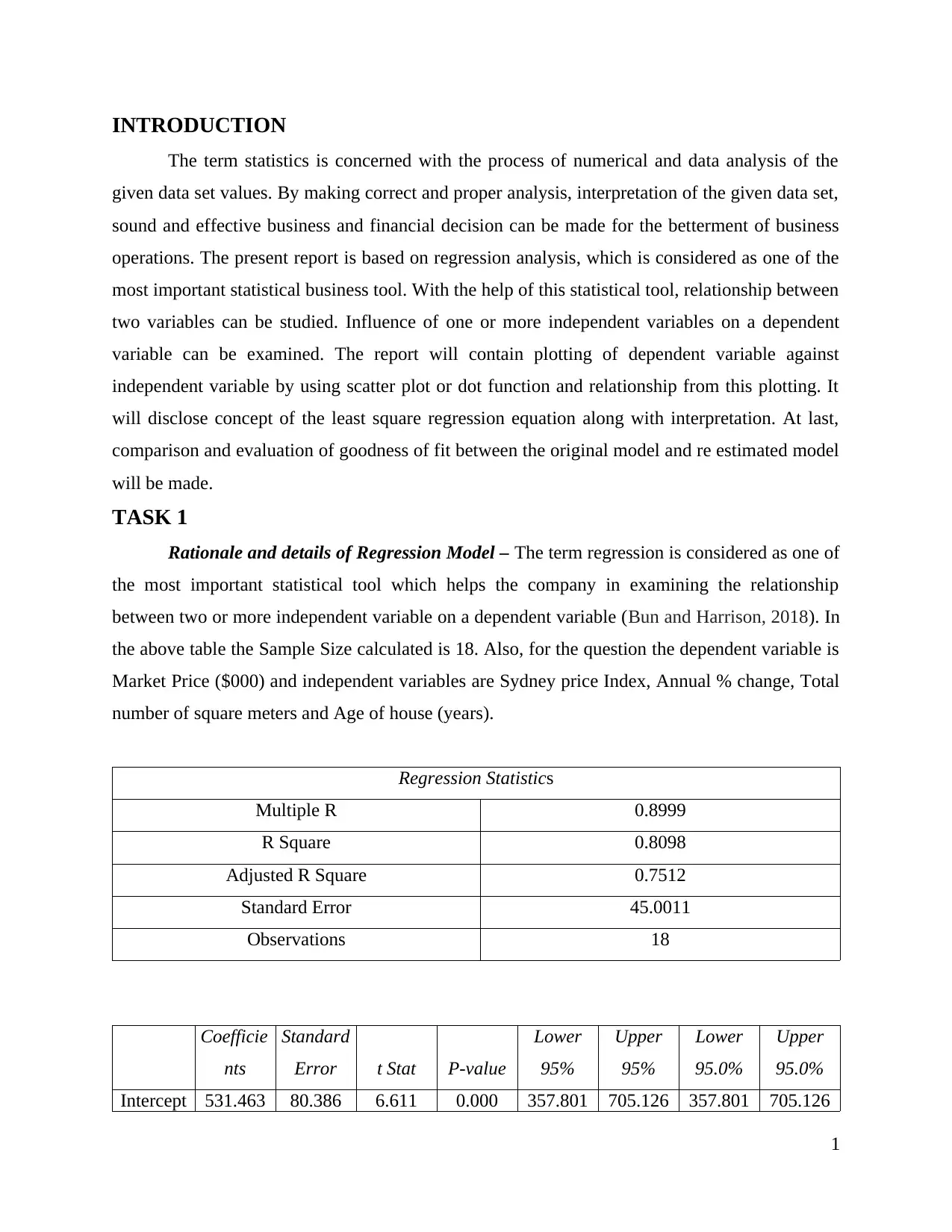
Rationale and details of Regression Model – The term regression is considered as one of
the most important statistical tool which helps the company in examining the relationship
between two or more independent variable on a dependent variable (Bun and Harrison, 2018). In
the above table the Sample Size calculated is 18. Also, for the question the dependent variable is
Market Price ($000) and independent variables are Sydney price Index, Annual % change, Total
number of square meters and Age of house (years).
Regression Statistics
Multiple R 0.8999
R Square 0.8098
Adjusted R Square 0.7512
Standard Error 45.0011
Observations 18
Coefficie
nts
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 531.463 80.386 6.611 0.000 357.801 705.126 357.801 705.126
1
The term statistics is concerned with the process of numerical and data analysis of the
given data set values. By making correct and proper analysis, interpretation of the given data set,
sound and effective business and financial decision can be made for the betterment of business
operations. The present report is based on regression analysis, which is considered as one of the
most important statistical business tool. With the help of this statistical tool, relationship between
two variables can be studied. Influence of one or more independent variables on a dependent
variable can be examined. The report will contain plotting of dependent variable against
independent variable by using scatter plot or dot function and relationship from this plotting. It
will disclose concept of the least square regression equation along with interpretation. At last,
comparison and evaluation of goodness of fit between the original model and re estimated model
will be made.
TASK 1
Rationale and details of Regression Model – The term regression is considered as one of
the most important statistical tool which helps the company in examining the relationship
between two or more independent variable on a dependent variable (Bun and Harrison, 2018). In
the above table the Sample Size calculated is 18. Also, for the question the dependent variable is
Market Price ($000) and independent variables are Sydney price Index, Annual % change, Total
number of square meters and Age of house (years).
Regression Statistics
Multiple R 0.8999
R Square 0.8098
Adjusted R Square 0.7512
Standard Error 45.0011
Observations 18
Coefficie
nts
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 531.463 80.386 6.611 0.000 357.801 705.126 357.801 705.126
1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
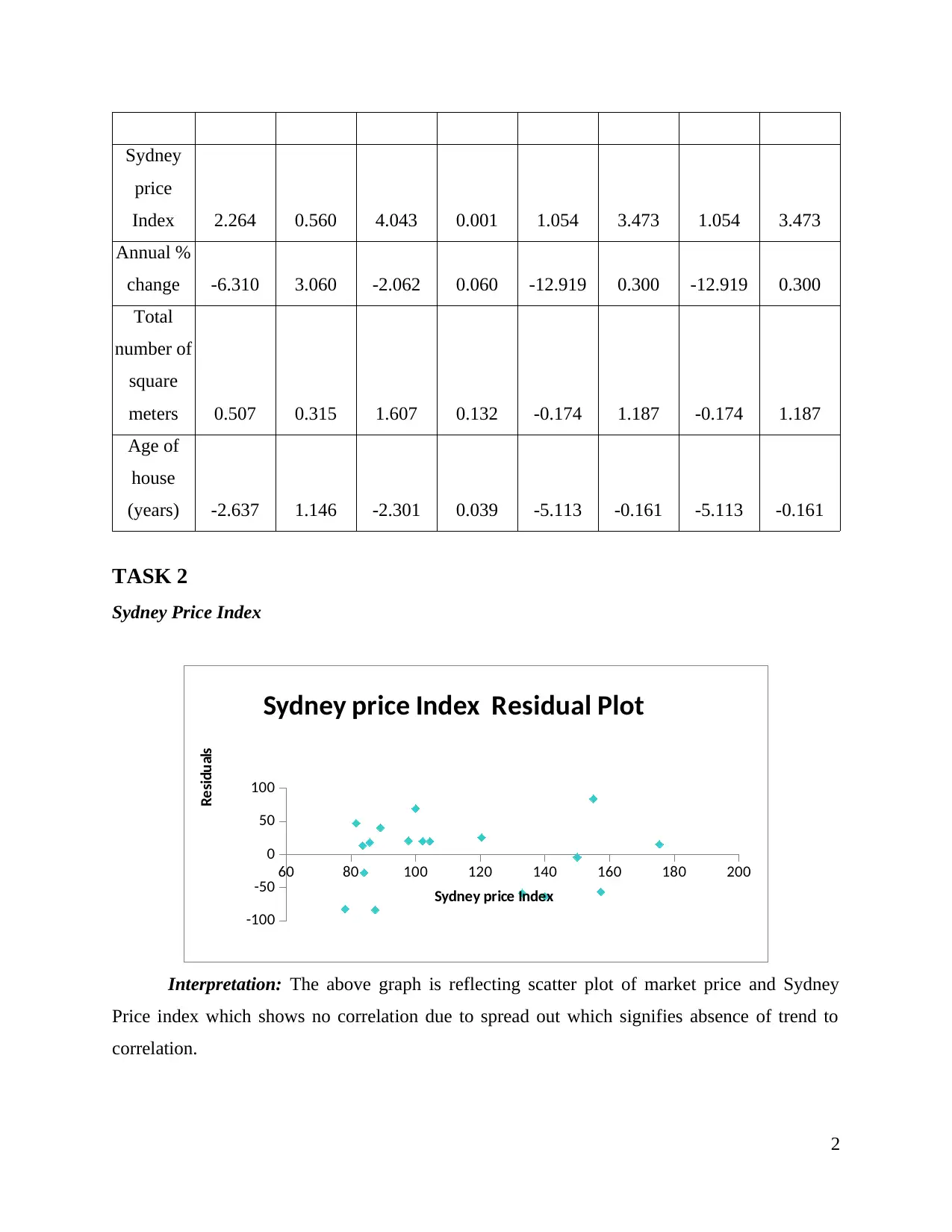
Sydney
price
Index 2.264 0.560 4.043 0.001 1.054 3.473 1.054 3.473
Annual %
change -6.310 3.060 -2.062 0.060 -12.919 0.300 -12.919 0.300
Total
number of
square
meters 0.507 0.315 1.607 0.132 -0.174 1.187 -0.174 1.187
Age of
house
(years) -2.637 1.146 -2.301 0.039 -5.113 -0.161 -5.113 -0.161
TASK 2
Sydney Price Index
60 80 100 120 140 160 180 200
-100
-50
0
50
100
Sydney price Index Residual Plot
Sydney price Index
Residuals
Interpretation: The above graph is reflecting scatter plot of market price and Sydney
Price index which shows no correlation due to spread out which signifies absence of trend to
correlation.
2
price
Index 2.264 0.560 4.043 0.001 1.054 3.473 1.054 3.473
Annual %
change -6.310 3.060 -2.062 0.060 -12.919 0.300 -12.919 0.300
Total
number of
square
meters 0.507 0.315 1.607 0.132 -0.174 1.187 -0.174 1.187
Age of
house
(years) -2.637 1.146 -2.301 0.039 -5.113 -0.161 -5.113 -0.161
TASK 2
Sydney Price Index
60 80 100 120 140 160 180 200
-100
-50
0
50
100
Sydney price Index Residual Plot
Sydney price Index
Residuals
Interpretation: The above graph is reflecting scatter plot of market price and Sydney
Price index which shows no correlation due to spread out which signifies absence of trend to
correlation.
2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
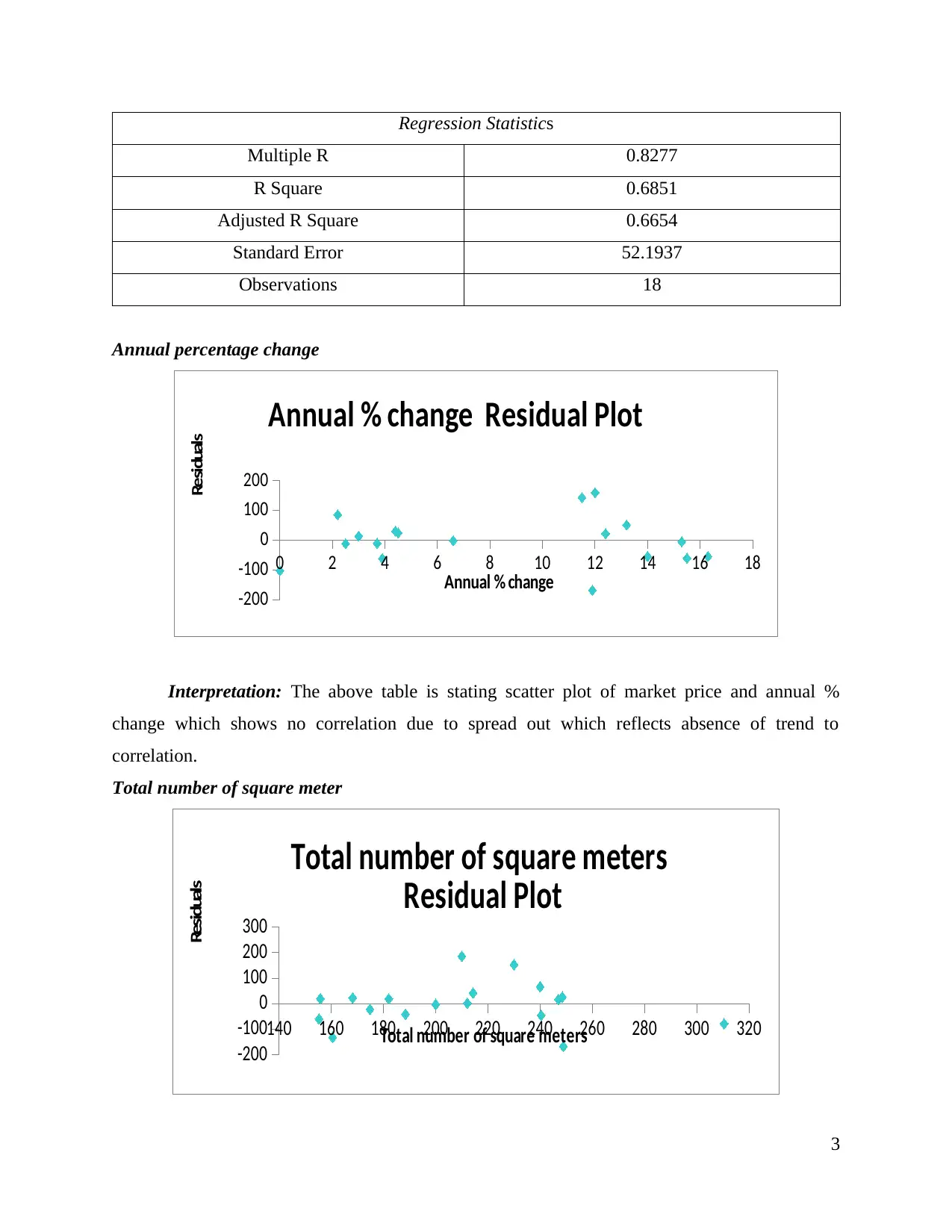
Regression Statistics
Multiple R 0.8277
R Square 0.6851
Adjusted R Square 0.6654
Standard Error 52.1937
Observations 18
Annual percentage change
0 2 4 6 8 10 12 14 16 18
-200
-100
0
100
200
Annual % change Residual Plot
Annual % change
Residuals
Interpretation: The above table is stating scatter plot of market price and annual %
change which shows no correlation due to spread out which reflects absence of trend to
correlation.
Total number of square meter
140 160 180 200 220 240 260 280 300 320
-200
-100
0
100
200
300
Total number of square meters
Residual Plot
Total number of square meters
Residuals
3
Multiple R 0.8277
R Square 0.6851
Adjusted R Square 0.6654
Standard Error 52.1937
Observations 18
Annual percentage change
0 2 4 6 8 10 12 14 16 18
-200
-100
0
100
200
Annual % change Residual Plot
Annual % change
Residuals
Interpretation: The above table is stating scatter plot of market price and annual %
change which shows no correlation due to spread out which reflects absence of trend to
correlation.
Total number of square meter
140 160 180 200 220 240 260 280 300 320
-200
-100
0
100
200
300
Total number of square meters
Residual Plot
Total number of square meters
Residuals
3
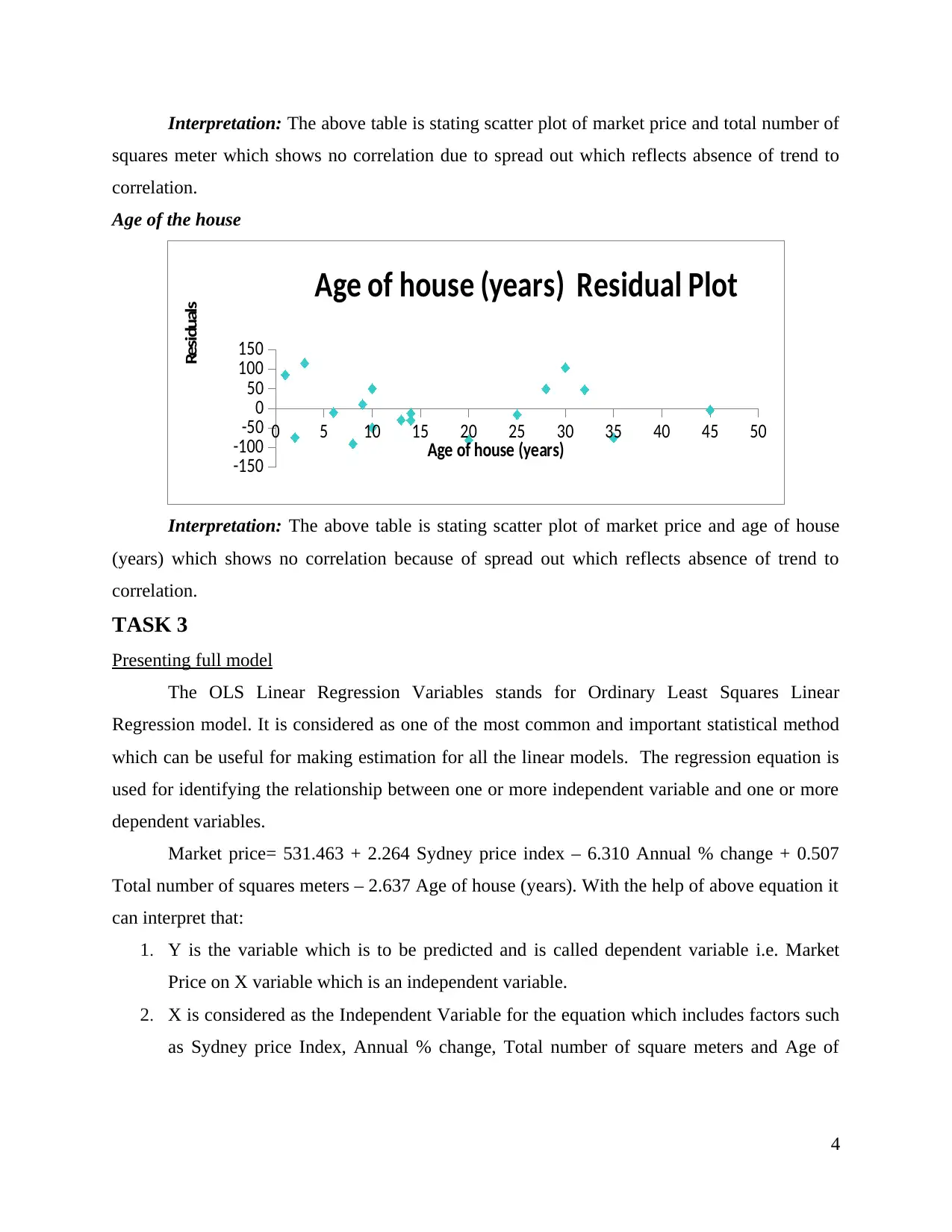
Interpretation: The above table is stating scatter plot of market price and total number of
squares meter which shows no correlation due to spread out which reflects absence of trend to
correlation.
Age of the house
0 5 10 15 20 25 30 35 40 45 50
-150
-100
-50
0
50
100
150
Age of house (years) Residual Plot
Age of house (years)
Residuals
Interpretation: The above table is stating scatter plot of market price and age of house
(years) which shows no correlation because of spread out which reflects absence of trend to
correlation.
TASK 3
Presenting full model
The OLS Linear Regression Variables stands for Ordinary Least Squares Linear
Regression model. It is considered as one of the most common and important statistical method
which can be useful for making estimation for all the linear models. The regression equation is
used for identifying the relationship between one or more independent variable and one or more
dependent variables.
Market price= 531.463 + 2.264 Sydney price index – 6.310 Annual % change + 0.507
Total number of squares meters – 2.637 Age of house (years). With the help of above equation it
can interpret that:
1. Y is the variable which is to be predicted and is called dependent variable i.e. Market
Price on X variable which is an independent variable.
2. X is considered as the Independent Variable for the equation which includes factors such
as Sydney price Index, Annual % change, Total number of square meters and Age of
4
squares meter which shows no correlation due to spread out which reflects absence of trend to
correlation.
Age of the house
0 5 10 15 20 25 30 35 40 45 50
-150
-100
-50
0
50
100
150
Age of house (years) Residual Plot
Age of house (years)
Residuals
Interpretation: The above table is stating scatter plot of market price and age of house
(years) which shows no correlation because of spread out which reflects absence of trend to
correlation.
TASK 3
Presenting full model
The OLS Linear Regression Variables stands for Ordinary Least Squares Linear
Regression model. It is considered as one of the most common and important statistical method
which can be useful for making estimation for all the linear models. The regression equation is
used for identifying the relationship between one or more independent variable and one or more
dependent variables.
Market price= 531.463 + 2.264 Sydney price index – 6.310 Annual % change + 0.507
Total number of squares meters – 2.637 Age of house (years). With the help of above equation it
can interpret that:
1. Y is the variable which is to be predicted and is called dependent variable i.e. Market
Price on X variable which is an independent variable.
2. X is considered as the Independent Variable for the equation which includes factors such
as Sydney price Index, Annual % change, Total number of square meters and Age of
4
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
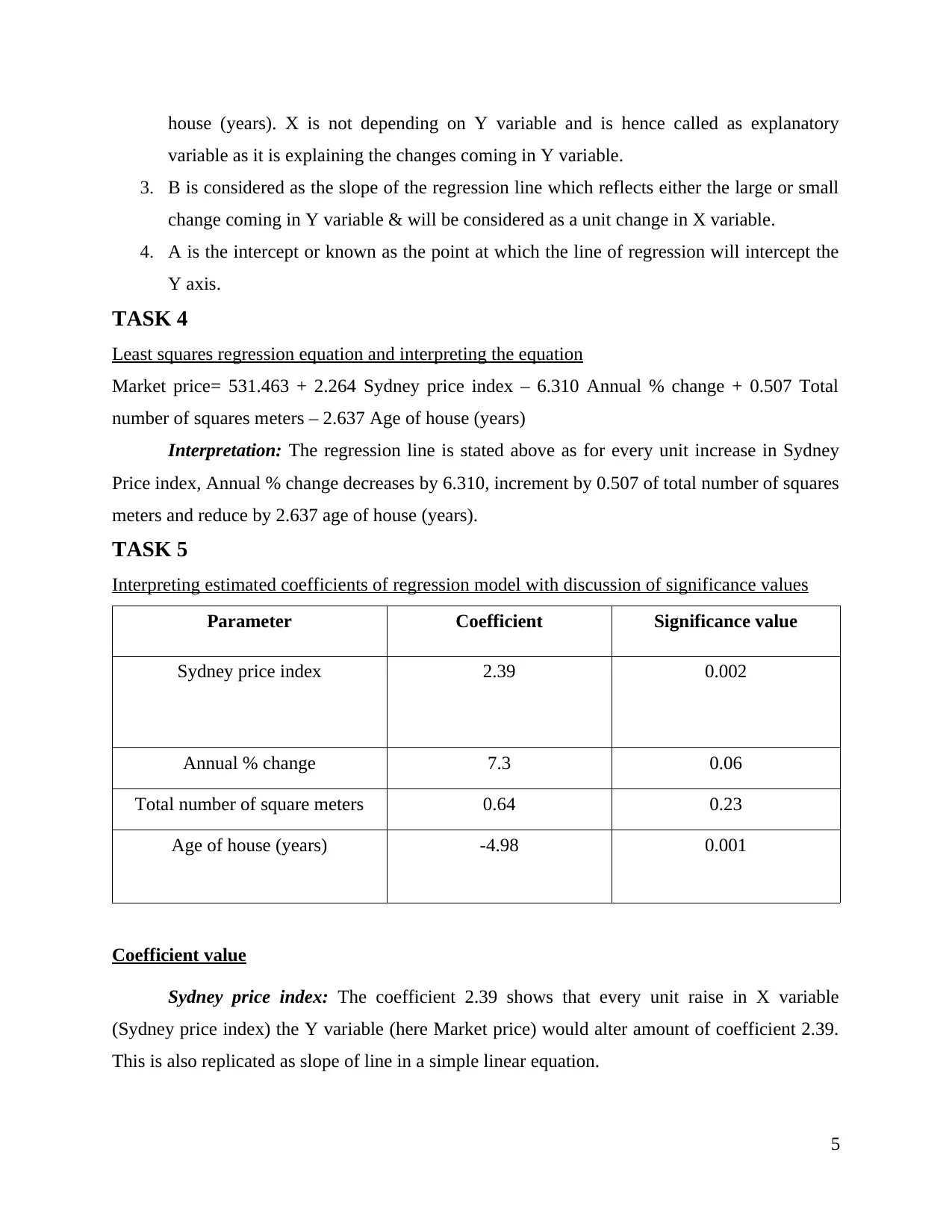
house (years). X is not depending on Y variable and is hence called as explanatory
variable as it is explaining the changes coming in Y variable.
3. B is considered as the slope of the regression line which reflects either the large or small
change coming in Y variable & will be considered as a unit change in X variable.
4. A is the intercept or known as the point at which the line of regression will intercept the
Y axis.
TASK 4
Least squares regression equation and interpreting the equation
Market price= 531.463 + 2.264 Sydney price index – 6.310 Annual % change + 0.507 Total
number of squares meters – 2.637 Age of house (years)
Interpretation: The regression line is stated above as for every unit increase in Sydney
Price index, Annual % change decreases by 6.310, increment by 0.507 of total number of squares
meters and reduce by 2.637 age of house (years).
TASK 5
Interpreting estimated coefficients of regression model with discussion of significance values
Parameter Coefficient Significance value
Sydney price index 2.39 0.002
Annual % change 7.3 0.06
Total number of square meters 0.64 0.23
Age of house (years) -4.98 0.001
Coefficient value
Sydney price index: The coefficient 2.39 shows that every unit raise in X variable
(Sydney price index) the Y variable (here Market price) would alter amount of coefficient 2.39.
This is also replicated as slope of line in a simple linear equation.
5
variable as it is explaining the changes coming in Y variable.
3. B is considered as the slope of the regression line which reflects either the large or small
change coming in Y variable & will be considered as a unit change in X variable.
4. A is the intercept or known as the point at which the line of regression will intercept the
Y axis.
TASK 4
Least squares regression equation and interpreting the equation
Market price= 531.463 + 2.264 Sydney price index – 6.310 Annual % change + 0.507 Total
number of squares meters – 2.637 Age of house (years)
Interpretation: The regression line is stated above as for every unit increase in Sydney
Price index, Annual % change decreases by 6.310, increment by 0.507 of total number of squares
meters and reduce by 2.637 age of house (years).
TASK 5
Interpreting estimated coefficients of regression model with discussion of significance values
Parameter Coefficient Significance value
Sydney price index 2.39 0.002
Annual % change 7.3 0.06
Total number of square meters 0.64 0.23
Age of house (years) -4.98 0.001
Coefficient value
Sydney price index: The coefficient 2.39 shows that every unit raise in X variable
(Sydney price index) the Y variable (here Market price) would alter amount of coefficient 2.39.
This is also replicated as slope of line in a simple linear equation.
5
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Annual % change: The coefficient 7.3 shows that every unit increases in X variable
(Annual % change) the Y variable (here Market price) would change amount of coefficient 7.3.
This is also known as slope of line in a simple linear equation.
Total number of square meters: The coefficient 0.64 reflects that every unit increases by
X variable (Total number of square meters) the Y variable (here Market price) would alter
amount of coefficient 0.64. This is also referred as slope of line in a simple linear equation.
Age of house (years): The coefficient -4.95 shows that every unit decreases by X
variable (Age of house (years)) the Y variable (here Market price) would alter amount of
coefficient -4.95 and replicated as slope of line in a simple linear equation.
Significance value
Null hypothesis: H0- There is no significant mean difference in the market price and the land
size in Sydney Price Index.
Alternative hypothesis: H0- There is significant mean difference in the market price and the
land size in total number of Sydney Price Index.
Null hypothesis: H0- There is no significant mean difference in the market price and the land
size in Annual % change.
Alternative hypothesis: H0- There is significant mean difference in the market price and the
land size in Annual % change.
Null hypothesis: H0- There is no significant mean difference in the market price and the land
size in Total Number of square meters.
Alternative hypothesis: H0- There is significant mean difference in the market price and the
land size in Total Number of square meters.
Null hypothesis: H0- There is no significant mean difference in the market price and the land
size in Age of house (years).
Alternative hypothesis: H0- There is significant mean difference in the market price and the
land size in Age of house (years).
6
(Annual % change) the Y variable (here Market price) would change amount of coefficient 7.3.
This is also known as slope of line in a simple linear equation.
Total number of square meters: The coefficient 0.64 reflects that every unit increases by
X variable (Total number of square meters) the Y variable (here Market price) would alter
amount of coefficient 0.64. This is also referred as slope of line in a simple linear equation.
Age of house (years): The coefficient -4.95 shows that every unit decreases by X
variable (Age of house (years)) the Y variable (here Market price) would alter amount of
coefficient -4.95 and replicated as slope of line in a simple linear equation.
Significance value
Null hypothesis: H0- There is no significant mean difference in the market price and the land
size in Sydney Price Index.
Alternative hypothesis: H0- There is significant mean difference in the market price and the
land size in total number of Sydney Price Index.
Null hypothesis: H0- There is no significant mean difference in the market price and the land
size in Annual % change.
Alternative hypothesis: H0- There is significant mean difference in the market price and the
land size in Annual % change.
Null hypothesis: H0- There is no significant mean difference in the market price and the land
size in Total Number of square meters.
Alternative hypothesis: H0- There is significant mean difference in the market price and the
land size in Total Number of square meters.
Null hypothesis: H0- There is no significant mean difference in the market price and the land
size in Age of house (years).
Alternative hypothesis: H0- There is significant mean difference in the market price and the
land size in Age of house (years).
6
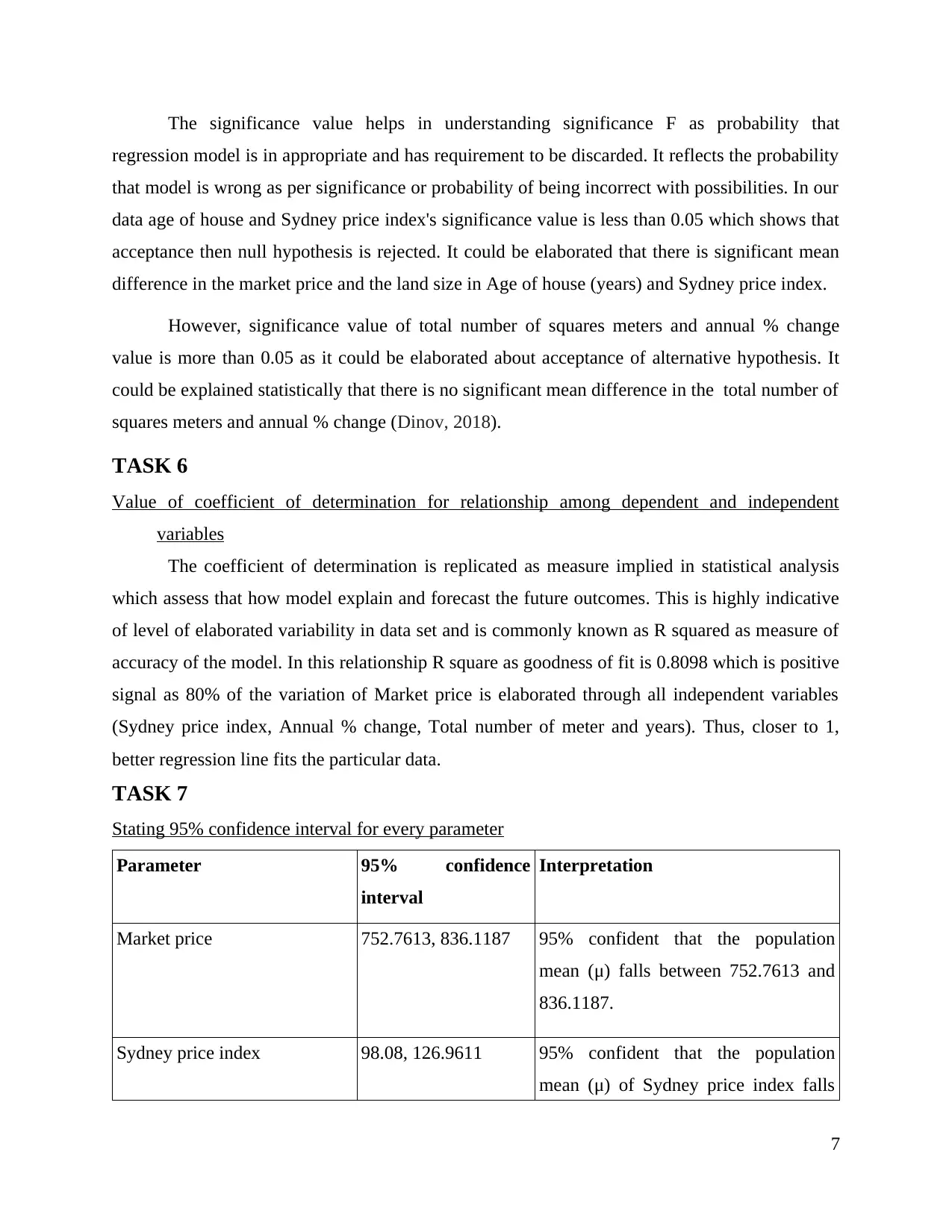
The significance value helps in understanding significance F as probability that
regression model is in appropriate and has requirement to be discarded. It reflects the probability
that model is wrong as per significance or probability of being incorrect with possibilities. In our
data age of house and Sydney price index's significance value is less than 0.05 which shows that
acceptance then null hypothesis is rejected. It could be elaborated that there is significant mean
difference in the market price and the land size in Age of house (years) and Sydney price index.
However, significance value of total number of squares meters and annual % change
value is more than 0.05 as it could be elaborated about acceptance of alternative hypothesis. It
could be explained statistically that there is no significant mean difference in the total number of
squares meters and annual % change (Dinov, 2018).
TASK 6
Value of coefficient of determination for relationship among dependent and independent
variables
The coefficient of determination is replicated as measure implied in statistical analysis
which assess that how model explain and forecast the future outcomes. This is highly indicative
of level of elaborated variability in data set and is commonly known as R squared as measure of
accuracy of the model. In this relationship R square as goodness of fit is 0.8098 which is positive
signal as 80% of the variation of Market price is elaborated through all independent variables
(Sydney price index, Annual % change, Total number of meter and years). Thus, closer to 1,
better regression line fits the particular data.
TASK 7
Stating 95% confidence interval for every parameter
Parameter 95% confidence
interval
Interpretation
Market price 752.7613, 836.1187 95% confident that the population
mean (μ) falls between 752.7613 and
836.1187.
Sydney price index 98.08, 126.9611 95% confident that the population
mean (μ) of Sydney price index falls
7
regression model is in appropriate and has requirement to be discarded. It reflects the probability
that model is wrong as per significance or probability of being incorrect with possibilities. In our
data age of house and Sydney price index's significance value is less than 0.05 which shows that
acceptance then null hypothesis is rejected. It could be elaborated that there is significant mean
difference in the market price and the land size in Age of house (years) and Sydney price index.
However, significance value of total number of squares meters and annual % change
value is more than 0.05 as it could be elaborated about acceptance of alternative hypothesis. It
could be explained statistically that there is no significant mean difference in the total number of
squares meters and annual % change (Dinov, 2018).
TASK 6
Value of coefficient of determination for relationship among dependent and independent
variables
The coefficient of determination is replicated as measure implied in statistical analysis
which assess that how model explain and forecast the future outcomes. This is highly indicative
of level of elaborated variability in data set and is commonly known as R squared as measure of
accuracy of the model. In this relationship R square as goodness of fit is 0.8098 which is positive
signal as 80% of the variation of Market price is elaborated through all independent variables
(Sydney price index, Annual % change, Total number of meter and years). Thus, closer to 1,
better regression line fits the particular data.
TASK 7
Stating 95% confidence interval for every parameter
Parameter 95% confidence
interval
Interpretation
Market price 752.7613, 836.1187 95% confident that the population
mean (μ) falls between 752.7613 and
836.1187.
Sydney price index 98.08, 126.9611 95% confident that the population
mean (μ) of Sydney price index falls
7
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
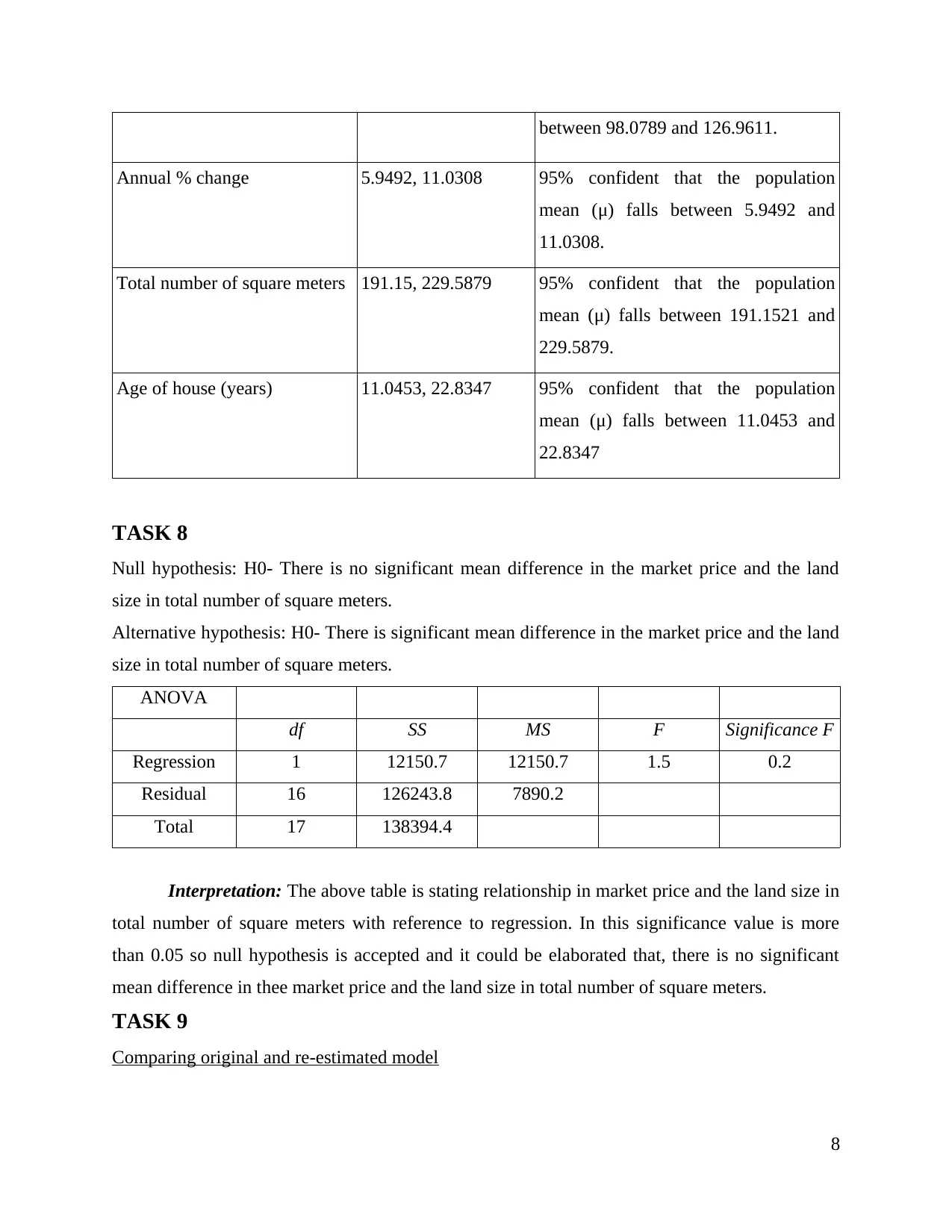
between 98.0789 and 126.9611.
Annual % change 5.9492, 11.0308 95% confident that the population
mean (μ) falls between 5.9492 and
11.0308.
Total number of square meters 191.15, 229.5879 95% confident that the population
mean (μ) falls between 191.1521 and
229.5879.
Age of house (years) 11.0453, 22.8347 95% confident that the population
mean (μ) falls between 11.0453 and
22.8347
TASK 8
Null hypothesis: H0- There is no significant mean difference in the market price and the land
size in total number of square meters.
Alternative hypothesis: H0- There is significant mean difference in the market price and the land
size in total number of square meters.
ANOVA
df SS MS F Significance F
Regression 1 12150.7 12150.7 1.5 0.2
Residual 16 126243.8 7890.2
Total 17 138394.4
Interpretation: The above table is stating relationship in market price and the land size in
total number of square meters with reference to regression. In this significance value is more
than 0.05 so null hypothesis is accepted and it could be elaborated that, there is no significant
mean difference in thee market price and the land size in total number of square meters.
TASK 9
Comparing original and re-estimated model
8
Annual % change 5.9492, 11.0308 95% confident that the population
mean (μ) falls between 5.9492 and
11.0308.
Total number of square meters 191.15, 229.5879 95% confident that the population
mean (μ) falls between 191.1521 and
229.5879.
Age of house (years) 11.0453, 22.8347 95% confident that the population
mean (μ) falls between 11.0453 and
22.8347
TASK 8
Null hypothesis: H0- There is no significant mean difference in the market price and the land
size in total number of square meters.
Alternative hypothesis: H0- There is significant mean difference in the market price and the land
size in total number of square meters.
ANOVA
df SS MS F Significance F
Regression 1 12150.7 12150.7 1.5 0.2
Residual 16 126243.8 7890.2
Total 17 138394.4
Interpretation: The above table is stating relationship in market price and the land size in
total number of square meters with reference to regression. In this significance value is more
than 0.05 so null hypothesis is accepted and it could be elaborated that, there is no significant
mean difference in thee market price and the land size in total number of square meters.
TASK 9
Comparing original and re-estimated model
8
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
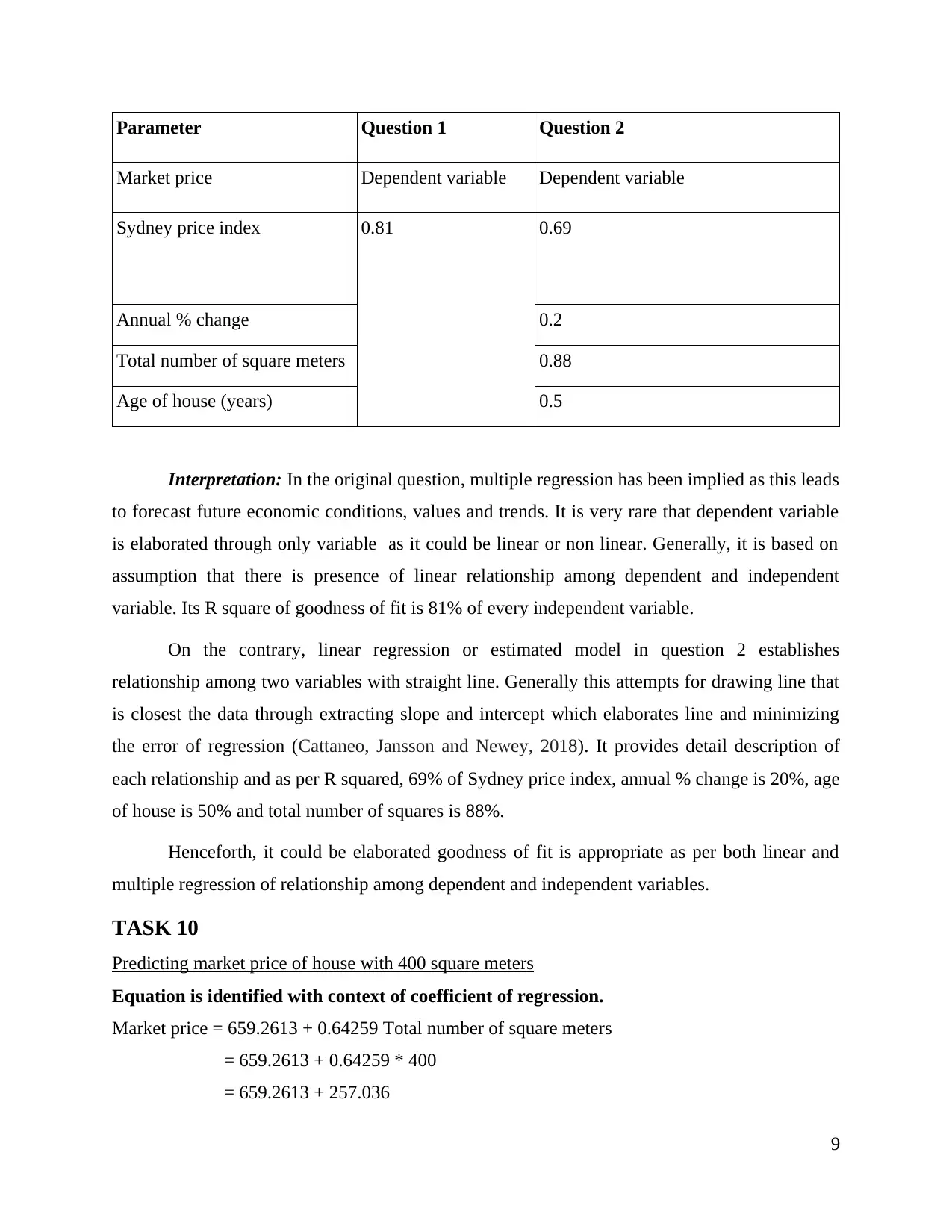
Parameter Question 1 Question 2
Market price Dependent variable Dependent variable
Sydney price index 0.81 0.69
Annual % change 0.2
Total number of square meters 0.88
Age of house (years) 0.5
Interpretation: In the original question, multiple regression has been implied as this leads
to forecast future economic conditions, values and trends. It is very rare that dependent variable
is elaborated through only variable as it could be linear or non linear. Generally, it is based on
assumption that there is presence of linear relationship among dependent and independent
variable. Its R square of goodness of fit is 81% of every independent variable.
On the contrary, linear regression or estimated model in question 2 establishes
relationship among two variables with straight line. Generally this attempts for drawing line that
is closest the data through extracting slope and intercept which elaborates line and minimizing
the error of regression (Cattaneo, Jansson and Newey, 2018). It provides detail description of
each relationship and as per R squared, 69% of Sydney price index, annual % change is 20%, age
of house is 50% and total number of squares is 88%.
Henceforth, it could be elaborated goodness of fit is appropriate as per both linear and
multiple regression of relationship among dependent and independent variables.
TASK 10
Predicting market price of house with 400 square meters
Equation is identified with context of coefficient of regression.
Market price = 659.2613 + 0.64259 Total number of square meters
= 659.2613 + 0.64259 * 400
= 659.2613 + 257.036
9
Market price Dependent variable Dependent variable
Sydney price index 0.81 0.69
Annual % change 0.2
Total number of square meters 0.88
Age of house (years) 0.5
Interpretation: In the original question, multiple regression has been implied as this leads
to forecast future economic conditions, values and trends. It is very rare that dependent variable
is elaborated through only variable as it could be linear or non linear. Generally, it is based on
assumption that there is presence of linear relationship among dependent and independent
variable. Its R square of goodness of fit is 81% of every independent variable.
On the contrary, linear regression or estimated model in question 2 establishes
relationship among two variables with straight line. Generally this attempts for drawing line that
is closest the data through extracting slope and intercept which elaborates line and minimizing
the error of regression (Cattaneo, Jansson and Newey, 2018). It provides detail description of
each relationship and as per R squared, 69% of Sydney price index, annual % change is 20%, age
of house is 50% and total number of squares is 88%.
Henceforth, it could be elaborated goodness of fit is appropriate as per both linear and
multiple regression of relationship among dependent and independent variables.
TASK 10
Predicting market price of house with 400 square meters
Equation is identified with context of coefficient of regression.
Market price = 659.2613 + 0.64259 Total number of square meters
= 659.2613 + 0.64259 * 400
= 659.2613 + 257.036
9

= $916.2973
CONCLUSION
On basis of above report it could be concluded that regression helps in extracting
relationship among dependent and independent variable. It has shown importance of confidence
interval with 95% within 18 sample of House price Index (a) (b); Brisbane, Sydney and
Melbourne, 2002 – 03 to 2016 – 17 with context to significance value.
10
CONCLUSION
On basis of above report it could be concluded that regression helps in extracting
relationship among dependent and independent variable. It has shown importance of confidence
interval with 95% within 18 sample of House price Index (a) (b); Brisbane, Sydney and
Melbourne, 2002 – 03 to 2016 – 17 with context to significance value.
10
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 12
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





