Analysis of Economic Order Quantity and Inventory Costs

This assignment involves a detailed analysis of Economic Order Quantity (EOQ), a method used to determine the optimal order quantity that minimizes total inventory costs. The study includes an examination of the effect of different variables, such as demand, cost, and pricing, on inventory management. A comparison of EOQ with variable costs is also presented, highlighting the importance of considering both in decision-making processes.

STATISTICS FOR
MANAGEMENT

Table of Contents
INTRODUCTION................................................................................................................................1
TASK 1.................................................................................................................................................1
A. Testing statistical significant difference in earnings of men and women in public sector..........1
B. Testing statistical significant difference in earnings of men and women in private sector.........2
C. Earning Time chart for each group for the period of 2009-2016................................................3
D. Determining annual growth rate in earnings for all the groups using above charts...................5
TASK 2.................................................................................................................................................7
SECTION A..........................................................................................................................................7
2.1 Presenting data in comprehensible form....................................................................................7
2.2 (i) Average marks of the students to assess their performance..................................................7
2.2 (ii) Measuring dispersion using accepted dispersion measures.................................................8
2.3 Interpreting and explaining the findings and determining association......................................9
SECTION B........................................................................................................................................10
2.4 Presenting scatter graph with line of best fit............................................................................10
TASK 3...............................................................................................................................................11
B..........................................................................................................................................................11
A. Number of deliveries.................................................................................................................11
B. Number of bottles of olive oil in each delivery.........................................................................11
C. Economic order quantity (EOQ)...............................................................................................11
TASK 4...............................................................................................................................................12
4.1 Showing charts.........................................................................................................................12
(i) Bar chart....................................................................................................................................12
(ii) Pie chart...................................................................................................................................13
4.2 Relationship between number of bedrooms and house prices.................................................14
CONCLUSION..................................................................................................................................14
REFERENCES...................................................................................................................................16

Index of Figures
Figure 1Men's yearly earnings in public sector....................................................................................3
Figure 2 Women's yearly earnings in public sector..............................................................................3
Figure 3 Men's yearly earnings in private sector..................................................................................4
Figure 4 Women's yearly earnings in private sector.............................................................................4
Figure 5 Growth rate of men’s earnings in public sector.....................................................................5
Figure 6 Growth rate of women’s earnings in public sector................................................................5
Figure 7 Growth rate of men’s earnings in private sector....................................................................6
Figure 8Growth rate of women’s earnings in private sector................................................................6
Figure 9 Scatter diagram with line of best fit.....................................................................................10
Figure 10 Bar graph presenting number of houses at different location............................................13
Figure 11Pie graph presenting number of houses at different location..............................................13
Figure 12Calculation of price of 2 & 3 bed room at different location..............................................14
Index of tables
table 1 calculation of average and standard deviation of earnings in public sector.............................1
table 2 calculation of average and standard deviation of earnings in public sector.............................2
table 3 arranging data in continuous series..........................................................................................7
table 4 calculation of median for the marks obtained by students.......................................................8
table 5 calculation of standard deviation of students marks.................................................................9
table 6 calculation of charges for one extra room at various location................................................14

INTRODUCTION
In today’s unpredictable market, it becomes too important for the managers to make good
quality decisions to stay competitive and assure long-run survival. The decision making process
involves extracting required information from the huge amount of data base and apply necessary
statistical tools and techniques for carrying out in-depth analysis. The current assignment aims to
apply different methods for hypothesis testing, descriptive statistics and measure dispersion
statistics to determine scatter in the series. Besides this, graphical presentation through different
graphs i.e. pie graph, bar graph and scatter plot will be constructed to present data effectively.
TASK 1
A. Testing statistical significant difference in earnings of men and women in public sector
Null hypothesis: There is no significant difference in the mean earnings of men and women in the
public sector.
Alternative hypothesis: There is significant difference in the mean earnings of men and women in
the public sector.
Level of significance: 5%
Table 1 Calculation of average and standard deviation of earnings in public sector
Year Public sector
Men Women
2009 30638 25224
2010 31264 26113
2011 31380 26470
2012 31816 26663
2013 32541 27338
2014 32878 27705
2015 33685 27900
2016 34011 28053
Sum 258213 215466
Average 32277 26933
Standard deviation 1204 988
Calculation of Test statistics: X1 – X2/√S12/(n-1) + (S22/n-1)
= (£32,277 – £26,933)/√(12042/8-1) + (9882/8-1)
= √£5,344/588.67
= 9.08
Z-value at 5% level of significance = 1.96
1 | P a g e

Test statistics 9.08 > 1.69 critical value
Therefore, the results make it clear that null hypothesis is rejected and alternative hypothesis
accepted indicating significant statistical difference in the mean earnings of men and women
working in public sector (Levin, 2008).
B. Testing statistical significant difference in earnings of men and women in private sector
Null hypothesis: There is no significant difference in the mean earnings of men and women in the
private sector.
Alternative hypothesis: There is significant difference in the mean earnings of men and women in
the private sector.
Table 2 Calculation of average and standard deviation of earnings in public sector
Year Private sector
Men Women
2009 27632 19551
2010 27000 19532
2011 27233 19565
2012 27705 20313
2013 28201 20698
2014 28442 21017
2015 28881 21403
2016 29679 22251
Sum 224773 164330
Average 28097 20541
Standard deviation 892 994
Calculation of Test statistics: X1 – X2/√S12/(n-1) + (S22/n-1)
= (£28,097 – £20,541)/√(8922/8-1) + (9942/8-1)
= √£7,555/504.84
= 14.95
Z-value at 5% level of significance = 1.96
Test statistics 14.95 > 1.69 critical value
As per the results, alternative hypothesis evident true because of higher test statistic above Z
value of 1.96. Hence, it can be said that there mean difference in the earnings of men and women
worth £7,555 is statistically significant and men employed in the private sector earns greater than
that of female workers (Keller and Warrack, 2003).
2 | P a g e

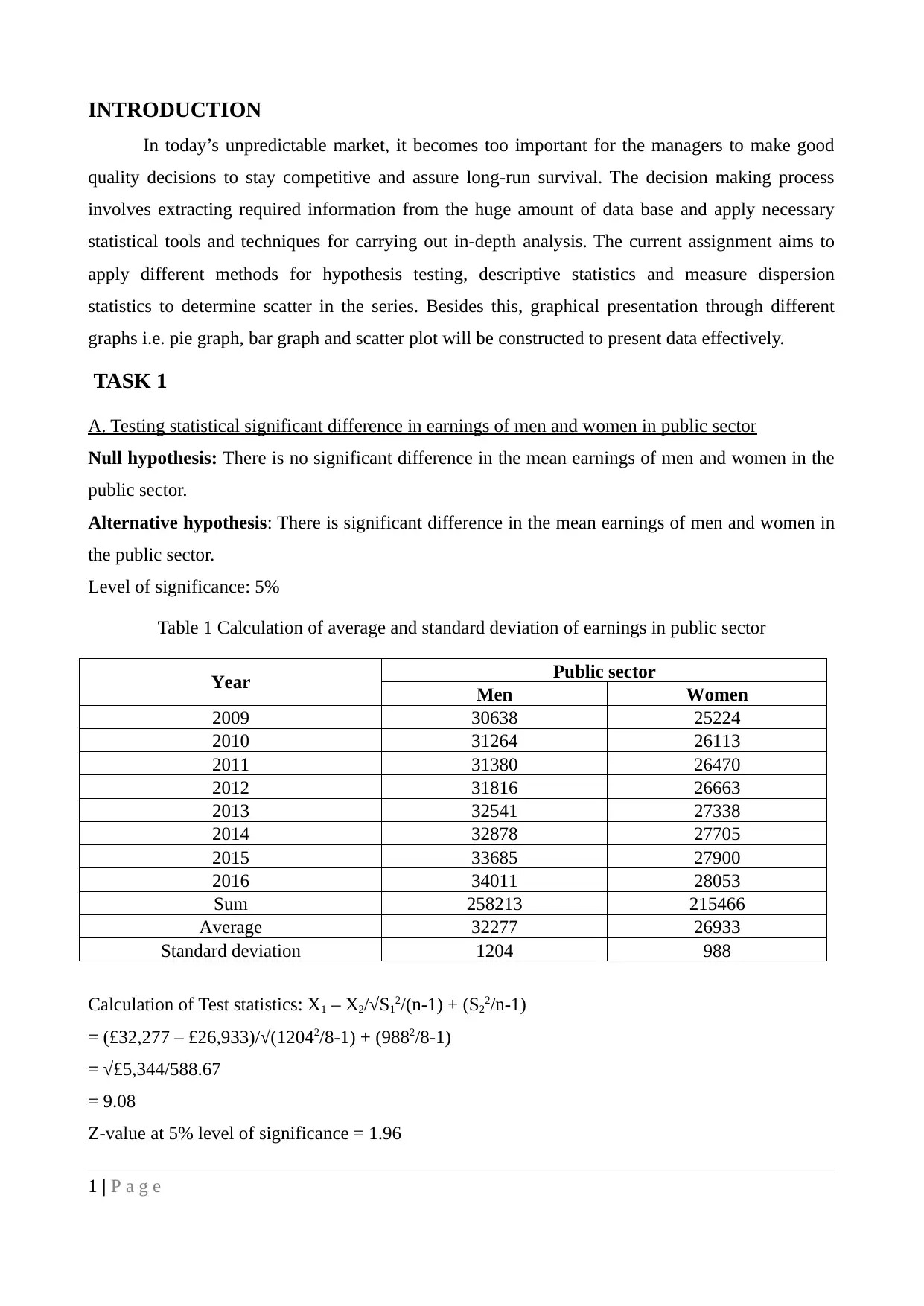
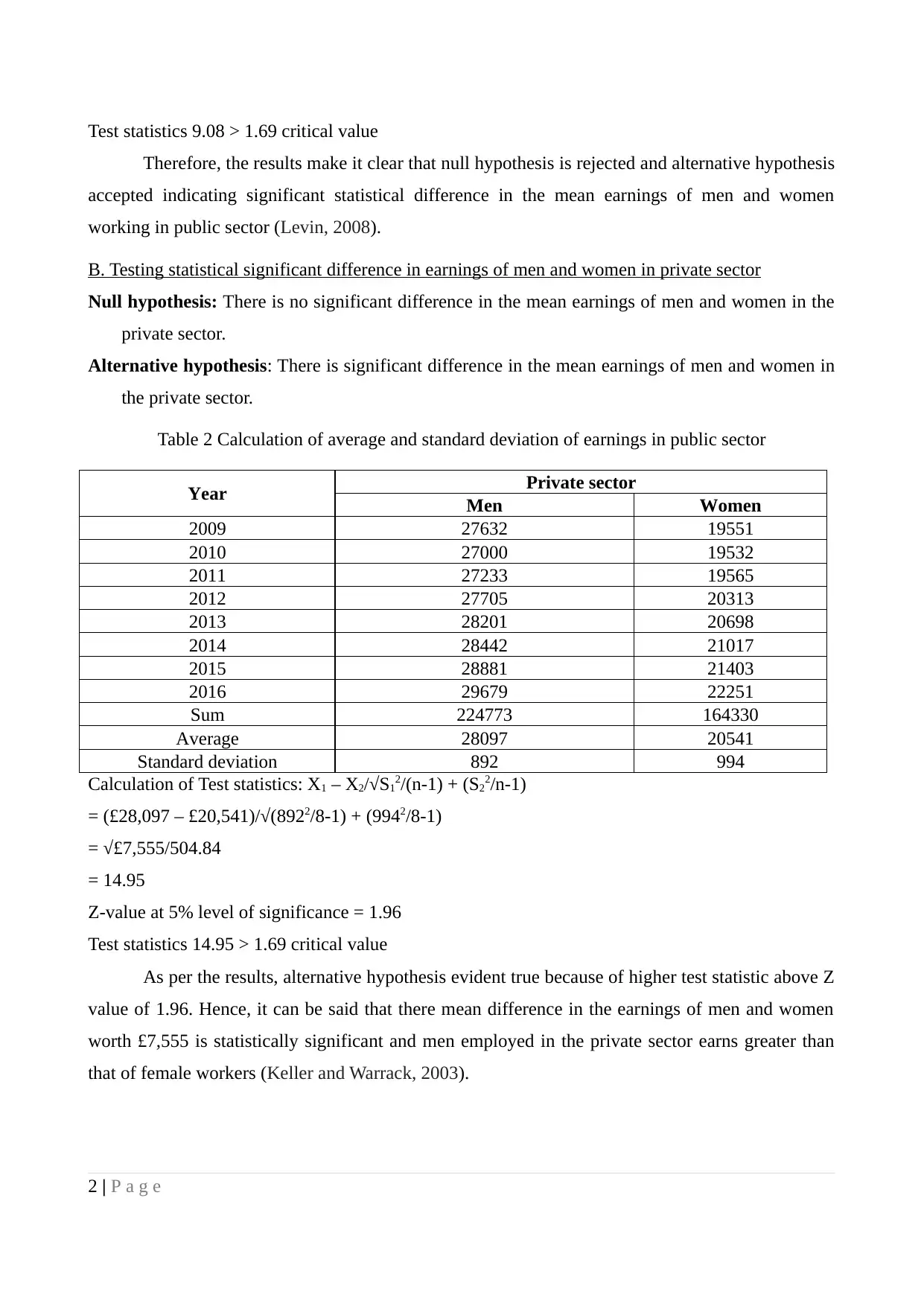
C. Earning Time chart for each group for the period of 2009-2016
Figure 1Men's yearly earnings in public sector
Figure 2 Women's yearly earnings in public sector
3 | P a g e

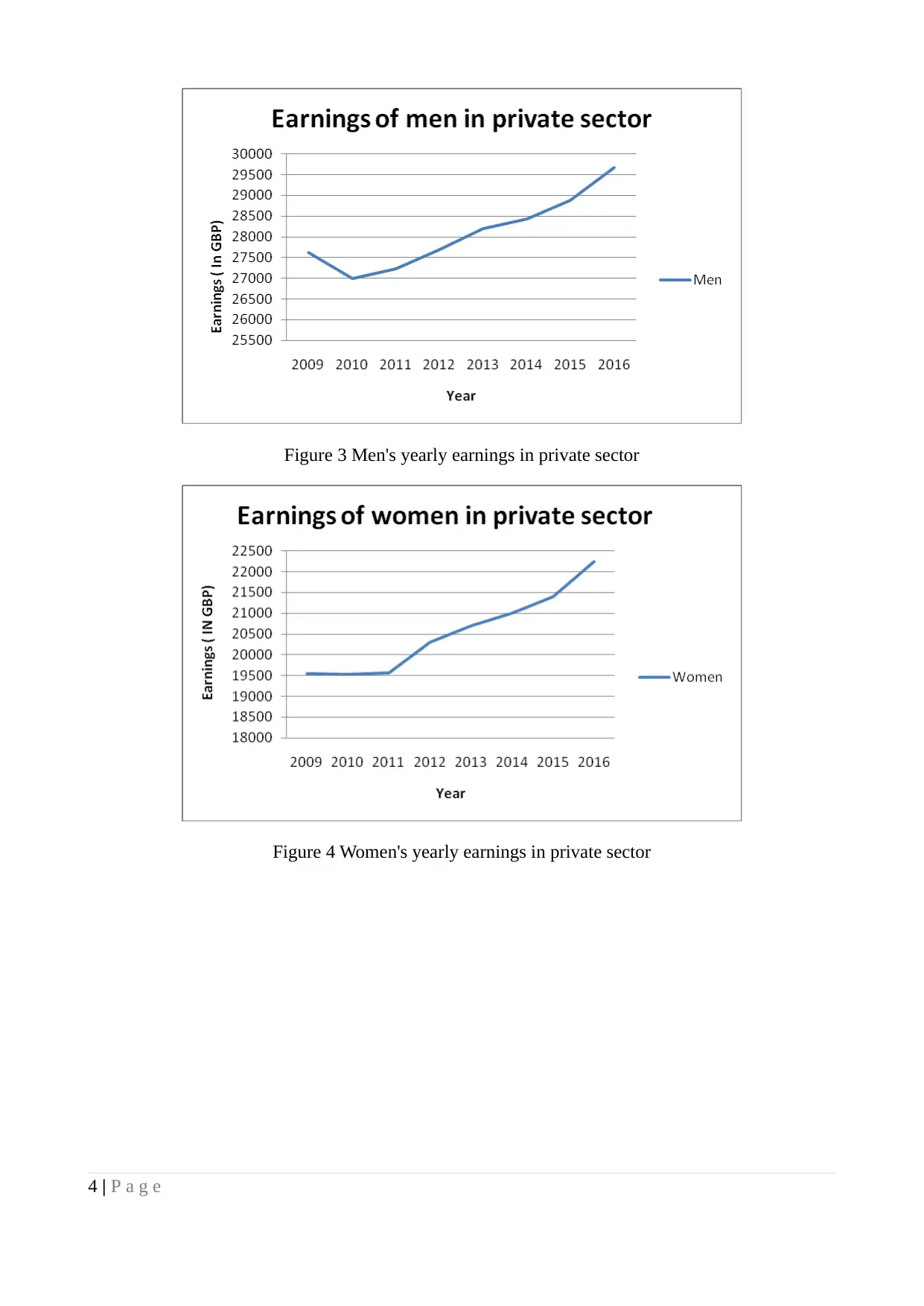
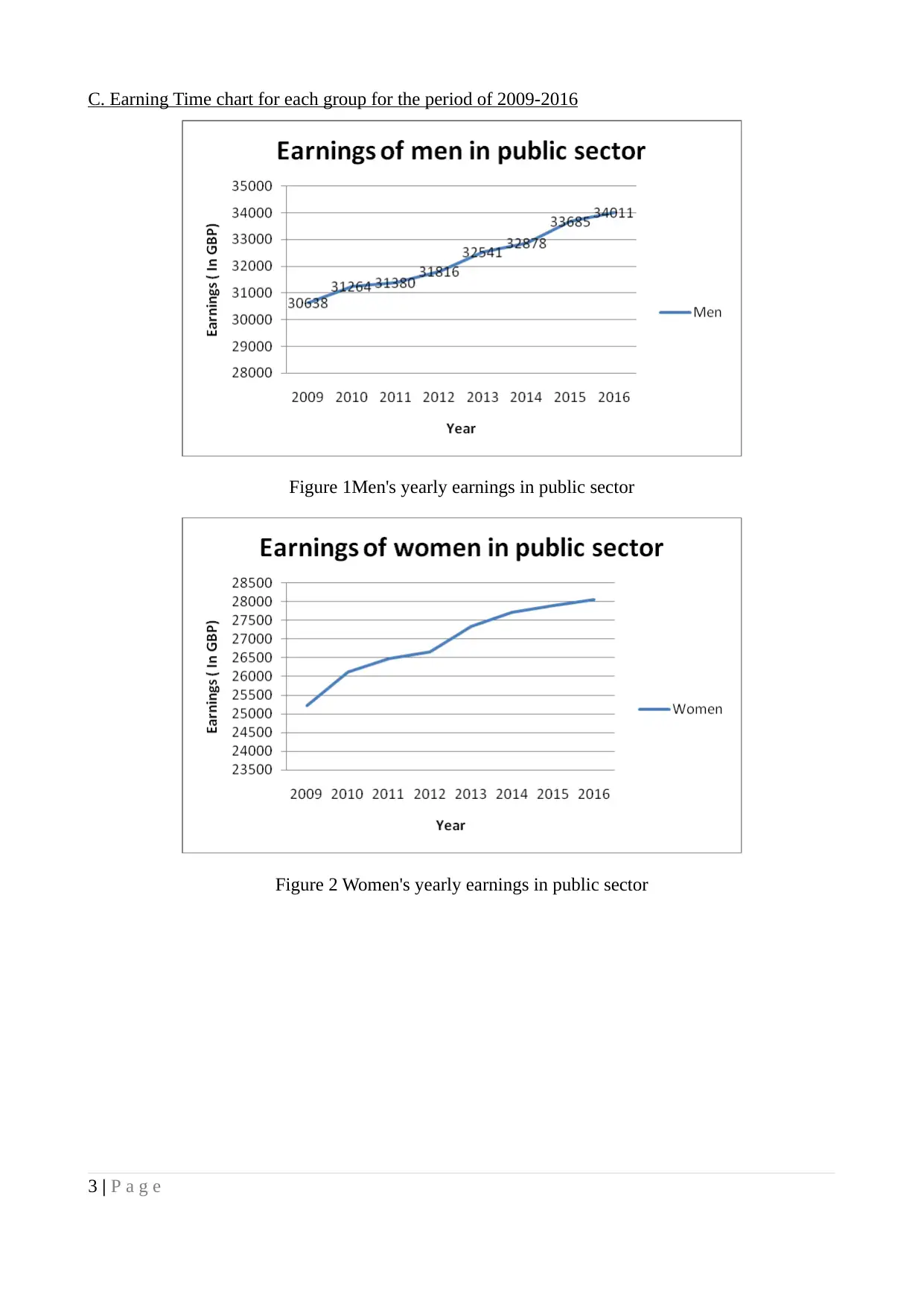
Figure 3 Men's yearly earnings in private sector
Figure 4 Women's yearly earnings in private sector
4 | P a g e

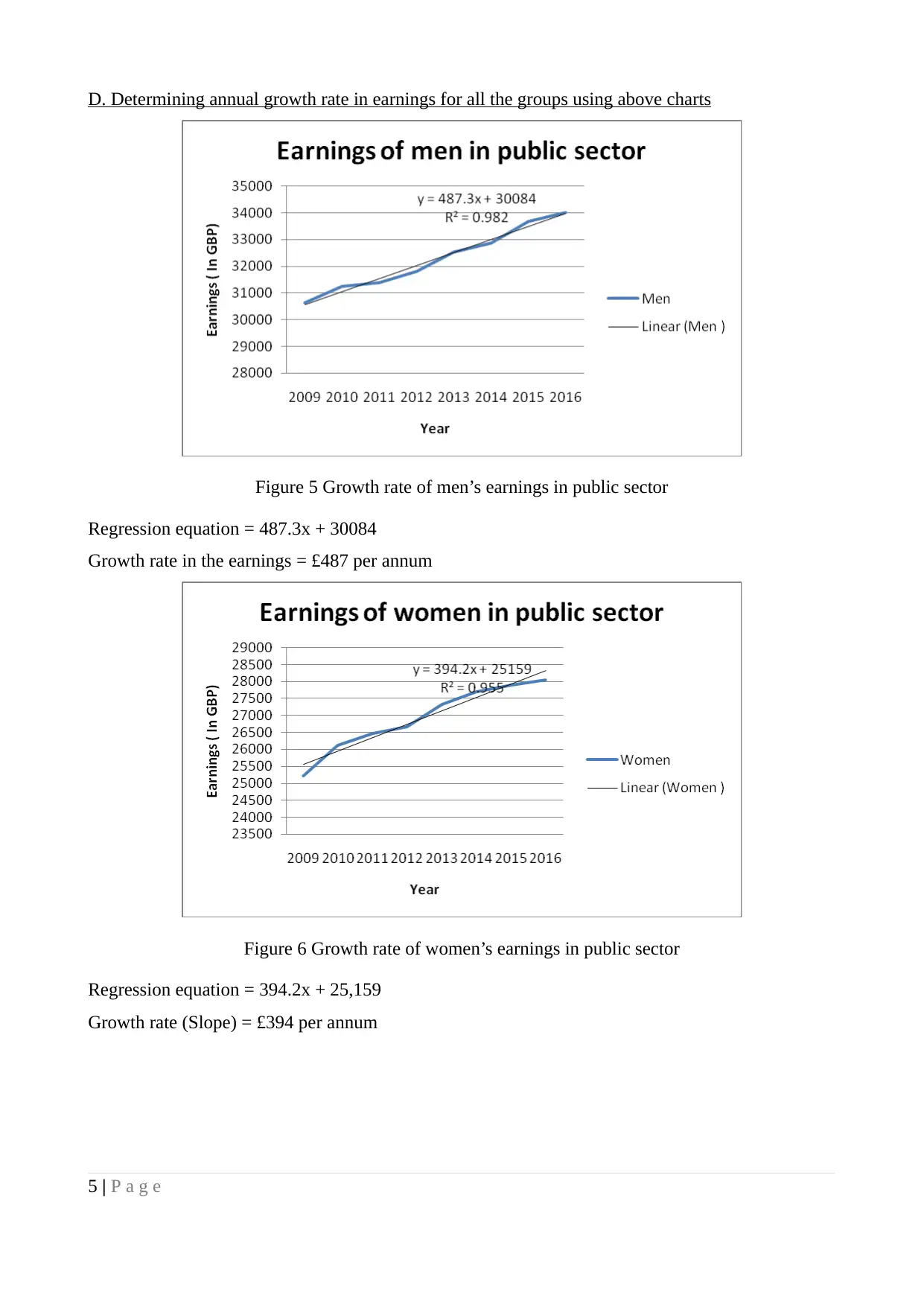
D. Determining annual growth rate in earnings for all the groups using above charts
Figure 5 Growth rate of men’s earnings in public sector
Regression equation = 487.3x + 30084
Growth rate in the earnings = £487 per annum
Figure 6 Growth rate of women’s earnings in public sector
Regression equation = 394.2x + 25,159
Growth rate (Slope) = £394 per annum
5 | P a g e

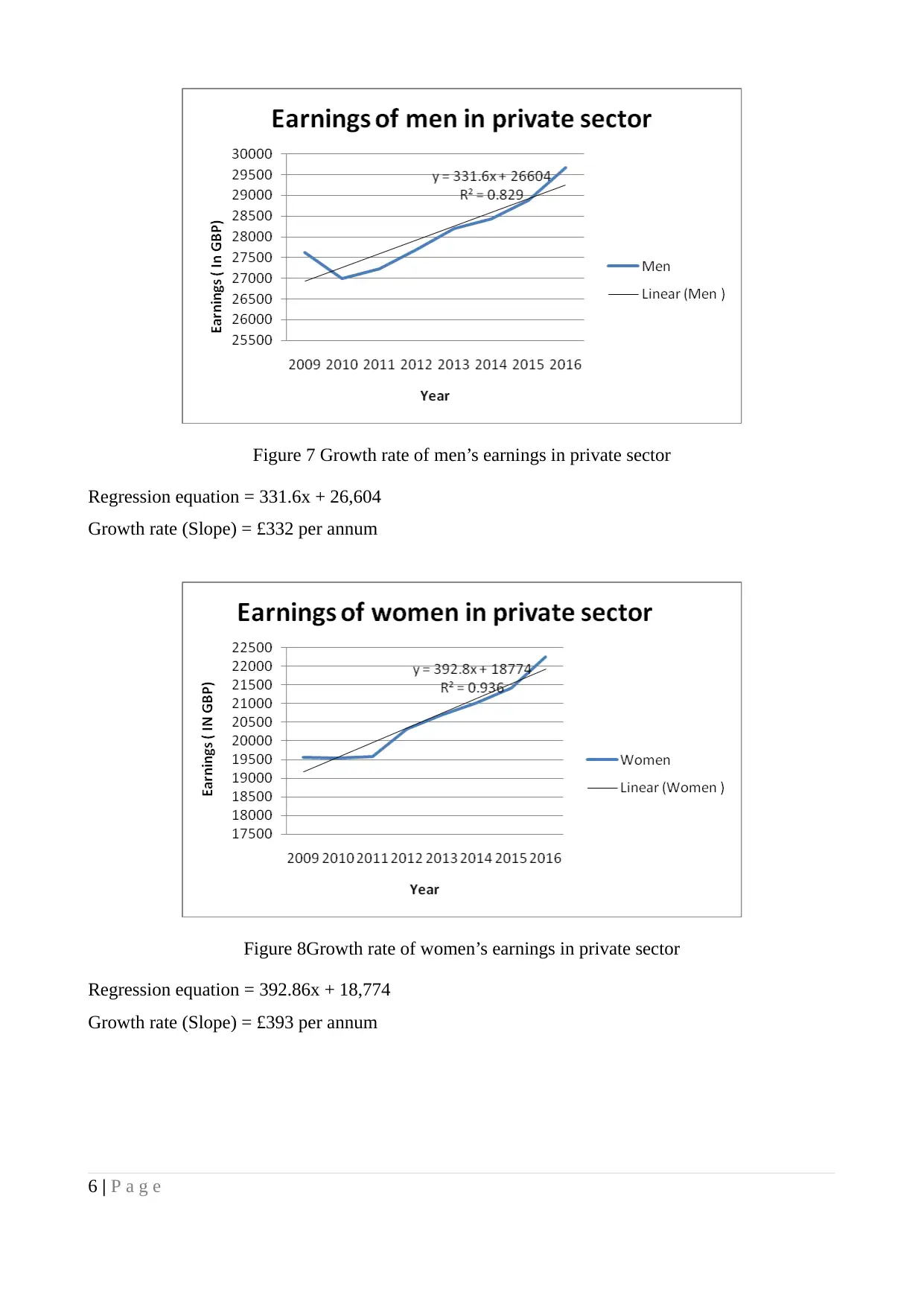
Figure 7 Growth rate of men’s earnings in private sector
Regression equation = 331.6x + 26,604
Growth rate (Slope) = £332 per annum
Figure 8Growth rate of women’s earnings in private sector
Regression equation = 392.86x + 18,774
Growth rate (Slope) = £393 per annum
6 | P a g e

TASK 2
SECTION A
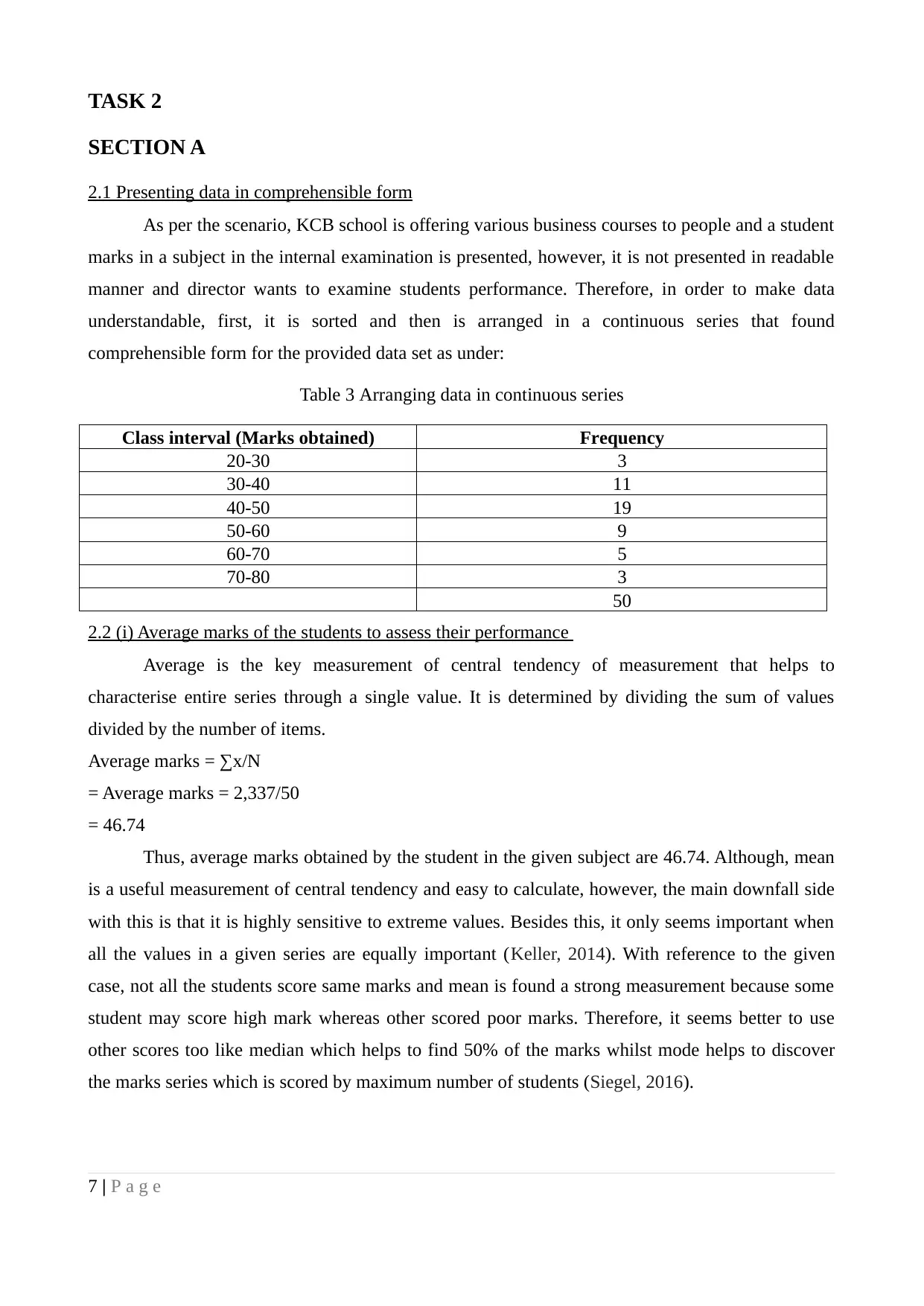
2.1 Presenting data in comprehensible form
As per the scenario, KCB school is offering various business courses to people and a student
marks in a subject in the internal examination is presented, however, it is not presented in readable
manner and director wants to examine students performance. Therefore, in order to make data
understandable, first, it is sorted and then is arranged in a continuous series that found
comprehensible form for the provided data set as under:
Table 3 Arranging data in continuous series
Class interval (Marks obtained) Frequency
20-30 3
30-40 11
40-50 19
50-60 9
60-70 5
70-80 3
50
2.2 (i) Average marks of the students to assess their performance
Average is the key measurement of central tendency of measurement that helps to
characterise entire series through a single value. It is determined by dividing the sum of values
divided by the number of items.
Average marks = ∑x/N
= Average marks = 2,337/50
= 46.74
Thus, average marks obtained by the student in the given subject are 46.74. Although, mean
is a useful measurement of central tendency and easy to calculate, however, the main downfall side
with this is that it is highly sensitive to extreme values. Besides this, it only seems important when
all the values in a given series are equally important (Keller, 2014). With reference to the given
case, not all the students score same marks and mean is found a strong measurement because some
student may score high mark whereas other scored poor marks. Therefore, it seems better to use
other scores too like median which helps to find 50% of the marks whilst mode helps to discover
the marks series which is scored by maximum number of students (Siegel, 2016).
7 | P a g e

Table 4 Calculation of median for the marks obtained by students
Class interval (Marks
obtained) Frequency
Cumulative frequency (CF)
20-30 3 3
30-40 11 14
40-50 19 33
50-60 9 42
60-70 5 47
70-80 3 50
50
Median (m) = Value of (N/2)th item
= value of (50/2)th item
= value of 25th item
It lies in the class interval of 40-50 marks with CF of 33.
M = L1 + [(N/2-c)/F]*i
Here: L1: Lower class interval of median series
N = ∑F
c: CF of previous class interval
F: Frequency
i: Class interval
= 40 + [(50/2-14)/19]*10
= 45.78
Mode: Maximum number of student scored marks 40 - 50 because its frequency is highest
with total of 19 students.
Strengths Weaknesses
Median  Middle value
 Not sensitive to the outliers
 Difficult to generalize
 Takes a lengthy time in calculation for
the large amount of data (Jessop, 2016)
Mode  Present most frequent value  Difficult to determine for discreet sets
2.2 (ii) Measuring dispersion using accepted dispersion measures
Dispersion measures are used to find out how extremely the values in a series are scattered
from the average value. Standard deviation is the best way of measuring dispersion which expresses
that how much the values of a group differs from mean (Jurado, Ludvigson and Ng, 2015).
8 | P a g e

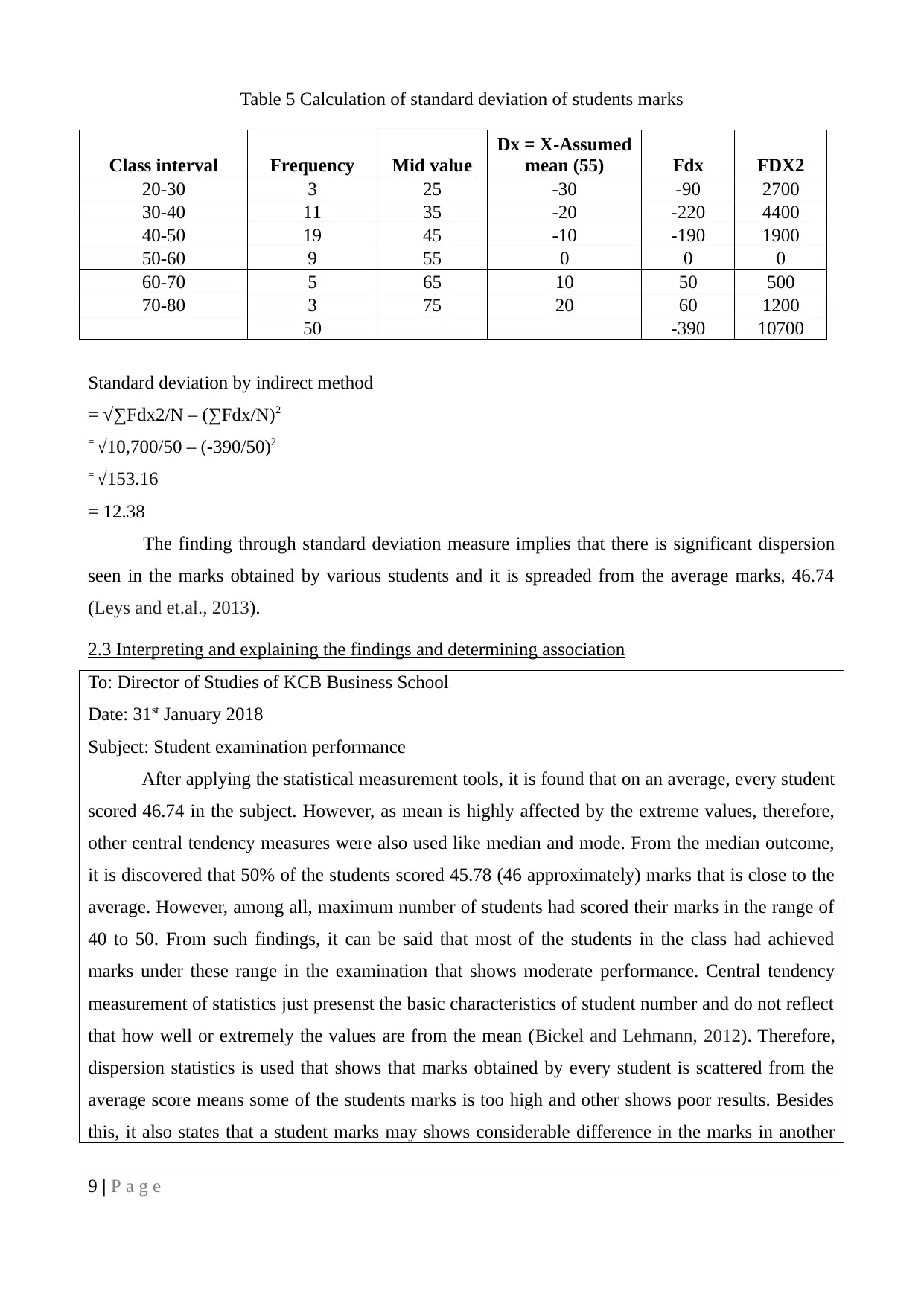
Table 5 Calculation of standard deviation of students marks
Class interval Frequency Mid value
Dx = X-Assumed
mean (55) Fdx FDX2
20-30 3 25 -30 -90 2700
30-40 11 35 -20 -220 4400
40-50 19 45 -10 -190 1900
50-60 9 55 0 0 0
60-70 5 65 10 50 500
70-80 3 75 20 60 1200
50 -390 10700
Standard deviation by indirect method
= √∑Fdx2/N – (∑Fdx/N)2
= √10,700/50 – (-390/50)2
= √153.16
= 12.38
The finding through standard deviation measure implies that there is significant dispersion
seen in the marks obtained by various students and it is spreaded from the average marks, 46.74
(Leys and et.al., 2013).
2.3 Interpreting and explaining the findings and determining association
To: Director of Studies of KCB Business School
Date: 31st January 2018
Subject: Student examination performance
After applying the statistical measurement tools, it is found that on an average, every student
scored 46.74 in the subject. However, as mean is highly affected by the extreme values, therefore,
other central tendency measures were also used like median and mode. From the median outcome,
it is discovered that 50% of the students scored 45.78 (46 approximately) marks that is close to the
average. However, among all, maximum number of students had scored their marks in the range of
40 to 50. From such findings, it can be said that most of the students in the class had achieved
marks under these range in the examination that shows moderate performance. Central tendency
measurement of statistics just presenst the basic characteristics of student number and do not reflect
that how well or extremely the values are from the mean (Bickel and Lehmann, 2012). Therefore,
dispersion statistics is used that shows that marks obtained by every student is scattered from the
average score means some of the students marks is too high and other shows poor results. Besides
this, it also states that a student marks may shows considerable difference in the marks in another
9 | P a g e

subject. Hence, student performance found widely deviated. In order to determine relationship or
association between two different subjects, correlation coefficient can be used that shows the
strength, level and direction of relationship between two different variables.
SECTION B
2.4 Presenting scatter graph with line of best fit
Scatter graph visualizes relationship between two related variables through presenting them
graphically. Here, age and weight normally shows positive relationship means high age people
usually found with greater weight volume or vice-versa (Chandrasekaran and UMAPARVATHI,
2016). Here, scatter plot is designed with line of best fit assuming linear relationship between both
the variables as follows:
Figure 9 Scatter diagram with line of best fit
According to the graph, values fall near to the regression line that indicates that regression
statistics will make justifiable prediction of weight using age as an independent variable and no
outliers is seen in the plot (David and et.al., 2017).
Regression equationn: Y = 2.152(age) + 7.652
weight of 7 months aged children = 2.152 (7) + 7.652 = 22.716 lbs
weight of 8 months aged children = 2.152 (8) + 7.652 = 24.868 lbs
weight of 9 months aged children = 2.152 (9) + 7.652 = 27.02 lbs
10 | P a g e

TASK 3
B.
A supplier is delivering olive oil in every 12 days to a local supermarket store at a cost of 20
GBP. Demand for oil in a year is 450,000 and its cost of warehousing is 25% of the unit cost of 2
GBP. Out of 365 days in a year, supermarket store closed on 5 days, means it runs its operations in
360 days.
A. Number of deliveries
In order to find number of deliveries that the supplier is completing in a year, 360 working
days per annum is considered.
Number of delivery = Total working days in a year / Delivery period
= 360 days /12 days
= 30
Thus, in a year, supplier delivers goods 30 times to the supermarket to satisfy annual oil
demand.
B. Number of bottles of olive oil in each delivery
= Annual demand/number of deliveries
= 450,000/30
= 15,000 bottles
On each order, company places an order of 15000 bottles of olive oil.
C. Economic order quantity (EOQ)
Economic Order Quantity (EOQ) helps to identify the number of units that a firm must place
to minimize their inventory cost including both the storage and ordering cost. It is used as a
continuous inventory system to monitor the level of inventory and identify the ordering level to
reduce total cost (Chen, Cárdenas and Teng, 2014).
EOQ = √2AO/c
A: Annual demand of goods, 450,000 units
O: Ordering cost per order, £20
C: Carrying cost of the item each unit, £0.50
= √ (2 * 450,000*£20)/£0.50
= √£18,000,000/£0.50
= √£36,000,000
= 6000 bottles
11 | P a g e

Calculation of total cost under current system
Average stock = (1/2 of 15000) = 7500 bottles of olive oil
Annual holding costs = 7500 bottles*£0.50 = £3,750
Annual delivery costs = 30 delivery*£20 = £600
Total costs = £3750 + £600 = £4350
Calculation of total cost under Economic Order Quantity
Average stock = (1/2 of 6,000) = 3,000 bottles of olive oil
Annual holding costs = 3,000 bottles*£0.50 = £1,500
Annual delivery costs = (450,000/6,000) *£20 = £1,500
Total costs = £1,500 + £1,500 = £3,000
Considering the result, it is clear that although in EOQ method, annual delivery cost goes up
from the current cost of £600 to £1500, still, as annual caring cost is found with considerable
decline from £3,750 to £1,500 with a lower total cost of £3000 than current level of £4,350, hence,
it is better to recommend the firm to go for EOQ and place order of bulk of 6000 bottles of olive oil
(Roy, Sana and Chaudhuri, 2011).
TASK 4
4.1 Showing charts
Presenting data set in an appropriate graphical format is really helpful to improve understand
ability and make the data readable (Anderson, Sweeney and Williams, 2014). Rosaline is an estate
agent who collected information about number of houses at different locations with different
number of bedrooms, which can be shown graphically using pie and bar chart as follows:
(i) Bar chart
Bar chart presents the categorical data in rectangular bar forms in which, x-axis presents
values and y-axis presents categories (Graphical presentation in Statistics, 2017).
12 | P a g e

Figure 10 Bar graph presenting number of houses at different location
The above graph reported that Rosaline has maximum rooms available at Green Street and
lowest at Church Lane. Considering different number of bedrooms, in all the cases, Green Street
shows maximum number of houses to 8, 28, 37, 17 and 10.
(ii) Pie chart
Figure 11Pie graph presenting number of houses at different location
13 | P a g e

4.2 Relationship between number of bedrooms and house prices
As per the situation, it is believed house prices and bedroom numbers are related to each
other because for more number of rooms, greater prices are charged or vice-versa. Here, for the
given scenario, it is seen that at every place like Green Street, Church Lane and Eton Avenue, high
price is charge for 3-bed room house and the value of one extra room is found below:
Table 6 Calculation of charges for one extra room at various location
Bedroom Green street Church Lane Eton Avenue
2 600000 700000 750000
3 700000 850000 1000000
Value of extra room 100000.00 150000.00 250000.00
Figure 12Calculation of price of 2 & 3 bed room at different location
Thus, from the findings, it can be reported that at Eton Avenue, price is too high as for one
additional room, ocupier need to pay £250,000 additionally while it is just £150,000 and £100,000
at Church Lane and Green Street (Sharpe, De Veaux and Velleman, 2015).
CONCLUSION
From the research findings, it is examined that in both the public and private sector, mean
earnings of men is significant higher than that of women’s average annual earnings because their p-
value is greater than alpha. Besides this, analysis of student performance through central tendency
14 | P a g e

and dispersion measure demonstrates that their marks show high deviation. In addition, application
of Economic Order Quantity discovered that it represent the ordering level at which total inventory
cost is minimum. Evidencing it from the results, EOQ is found with total cost of £3,000, lower than
variable cost of inventor by £1,350. Lastly, it is discovered that at Eton Avenue, very high price is
charged for a 3-bed room as the difference is found to £250,000.
15 | P a g e

REFERENCES
Books and Journals
Anderson, D., Sweeney, D. and Williams, T., 2014. Modern business statistics with Microsoft Excel.
Nelson Education.
Bickel, P.J. and Lehmann, E.L., 2012. Descriptive statistics for nonparametric models. III.
Dispersion. In Selected Works of EL Lehmann. Springer, Boston, MA. pp. 499-518.
Chandrasekaran, N. and UMAPARVATHI, M., 2016. Statistics for Management. PHI Learning Pvt.
Ltd..
Chen, S.C., Cárdenas-Barrón, L.E. and Teng, J.T., 2014. Retailer’s economic order quantity when
the supplier offers conditionally permissible delay in payments link to order
quantity. International Journal of Production Economics. 155. pp.284-291.
DAVID, F. and et.al., 2017. BUSINESS STATISTICS PLUS PEARSON MYLAB STATISTICS WITH
PEARSON ETEXT. PEARSON EDUCATION LIMITED.
Jessop, A., 2016. StatsNotes: Some Statistics for Management Problems. World Scientific Books.
Jurado, K., Ludvigson, S.C. and Ng, S., 2015. Measuring uncertainty. American Economic Review.
105(3). pp.1177-1216.
Keller, G. and Warrack, B., 2003. Statistics for Management and Economics (with Info Trac).
Thomson.
Keller, G., 2014. Statistics for management and economics. Nelson Education.
Levin, R.I., 2008. Statistics for management. Pearson Education.
Leys, C. and et.al., 2013. Detecting outliers: Do not use standard deviation around the mean, use
absolute deviation around the median. Journal of Experimental Social Psychology. 49(4).
pp.764-766.
Roy, M.D., Sana, S.S. and Chaudhuri, K., 2011. An economic order quantity model of imperfect
quality items with partial backlogging. International Journal of Systems Science. 42(8).
pp.1409-1419.
Sharpe, N.D., De Veaux, R.D. and Velleman, P.F., 2015. Business statistics. Pearson.
Siegel, A., 2016. Practical business statistics. Academic Press.
Online
Graphical presentation in Statistics. 2017. [Online]. Available through: <
https://www.healthknowledge.org.uk/public-health-textbook/research-methods/1b-statistical-
methods/graphical-methods-statistics>.
16 | P a g e

17 | P a g e