Analysis of Statistics for Managerial Decisions Assignment Solution
VerifiedAdded on 2022/11/01
|10
|999
|63
Homework Assignment
AI Summary
This assignment solution for Statistics for Managerial Decisions addresses several statistical concepts. It begins with data analysis, including stem-and-leaf plots, frequency polygons, and histograms to visualize stock prices. The solution then delves into investment analysis, computing risk-adjusted returns using beta to compare stock performance. Furthermore, the assignment examines real estate data, analyzing apartment rentals across different cities. The solution also explores probability, addressing crop selection based on state yields. Finally, it includes the interpretation of normal probability plots and the computation of confidence intervals to determine the variables suitable for differentiating between patient categories, specifically in identifying heart disease based on overlapping intervals.

STATISTICS FOR MANGERIAL DECISIONS
STUDENT ID:
[Pick the date]
STUDENT ID:
[Pick the date]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
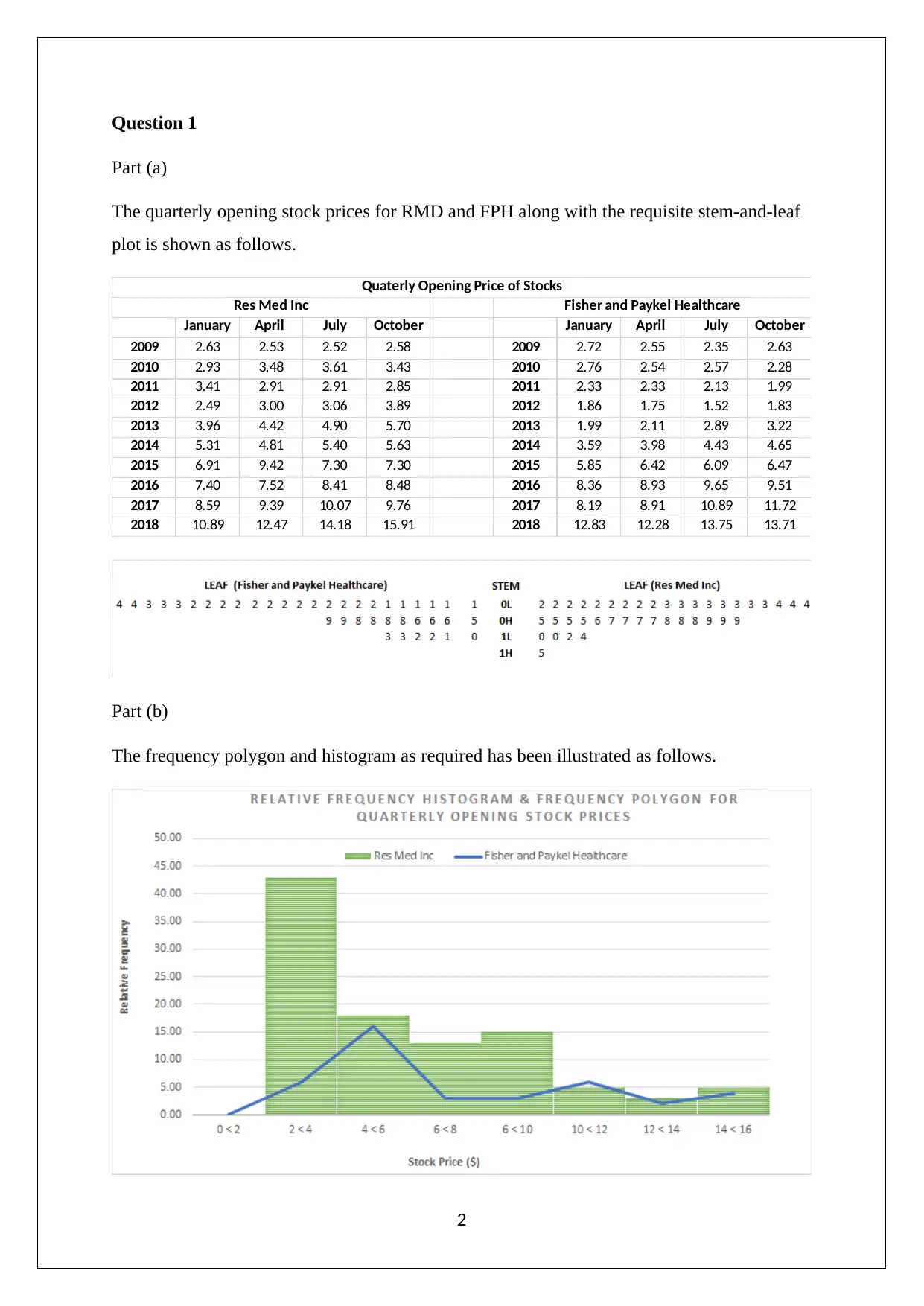
Question 1
Part (a)
The quarterly opening stock prices for RMD and FPH along with the requisite stem-and-leaf
plot is shown as follows.
January April July October January April July October
2009 2.63 2.53 2.52 2.58 2009 2.72 2.55 2.35 2.63
2010 2.93 3.48 3.61 3.43 2010 2.76 2.54 2.57 2.28
2011 3.41 2.91 2.91 2.85 2011 2.33 2.33 2.13 1.99
2012 2.49 3.00 3.06 3.89 2012 1.86 1.75 1.52 1.83
2013 3.96 4.42 4.90 5.70 2013 1.99 2.11 2.89 3.22
2014 5.31 4.81 5.40 5.63 2014 3.59 3.98 4.43 4.65
2015 6.91 9.42 7.30 7.30 2015 5.85 6.42 6.09 6.47
2016 7.40 7.52 8.41 8.48 2016 8.36 8.93 9.65 9.51
2017 8.59 9.39 10.07 9.76 2017 8.19 8.91 10.89 11.72
2018 10.89 12.47 14.18 15.91 2018 12.83 12.28 13.75 13.71
Quaterly Opening Price of Stocks
Res Med Inc Fisher and Paykel Healthcare
Part (b)
The frequency polygon and histogram as required has been illustrated as follows.
2
Part (a)
The quarterly opening stock prices for RMD and FPH along with the requisite stem-and-leaf
plot is shown as follows.
January April July October January April July October
2009 2.63 2.53 2.52 2.58 2009 2.72 2.55 2.35 2.63
2010 2.93 3.48 3.61 3.43 2010 2.76 2.54 2.57 2.28
2011 3.41 2.91 2.91 2.85 2011 2.33 2.33 2.13 1.99
2012 2.49 3.00 3.06 3.89 2012 1.86 1.75 1.52 1.83
2013 3.96 4.42 4.90 5.70 2013 1.99 2.11 2.89 3.22
2014 5.31 4.81 5.40 5.63 2014 3.59 3.98 4.43 4.65
2015 6.91 9.42 7.30 7.30 2015 5.85 6.42 6.09 6.47
2016 7.40 7.52 8.41 8.48 2016 8.36 8.93 9.65 9.51
2017 8.59 9.39 10.07 9.76 2017 8.19 8.91 10.89 11.72
2018 10.89 12.47 14.18 15.91 2018 12.83 12.28 13.75 13.71
Quaterly Opening Price of Stocks
Res Med Inc Fisher and Paykel Healthcare
Part (b)
The frequency polygon and histogram as required has been illustrated as follows.
2

Part (c)
As per the task, six publicly traded healthcare companies have been selected with market
capitalisation in excess of $ 100 million and the following bar chart is obtained from the
same.
Part (d)
In order to opine as to which stock is better from investment perspective, the risk adjusted
returns have to be computed. Beta is deployed as a measure of risk. Considering that three
year beta has been used, hence for returns computation also, the price appreciation during the
last three year ought to be considered.
Three year returns (RMD) = (16.30-8.30)/8.30 = 96.39%
Three year returns (FPH) = (15.45 -9.56)/9.56 = 61.61%
Also, RMD beta is 0.72 as compared to FPH beta of 1.21.
Hence, over the last three years, RMD has the lower risk and superior returns owing to which
this is the preferred bet.
Question 2
Part (a) “Mean, Median, Quartile First and Second”
3
As per the task, six publicly traded healthcare companies have been selected with market
capitalisation in excess of $ 100 million and the following bar chart is obtained from the
same.
Part (d)
In order to opine as to which stock is better from investment perspective, the risk adjusted
returns have to be computed. Beta is deployed as a measure of risk. Considering that three
year beta has been used, hence for returns computation also, the price appreciation during the
last three year ought to be considered.
Three year returns (RMD) = (16.30-8.30)/8.30 = 96.39%
Three year returns (FPH) = (15.45 -9.56)/9.56 = 61.61%
Also, RMD beta is 0.72 as compared to FPH beta of 1.21.
Hence, over the last three years, RMD has the lower risk and superior returns owing to which
this is the preferred bet.
Question 2
Part (a) “Mean, Median, Quartile First and Second”
3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
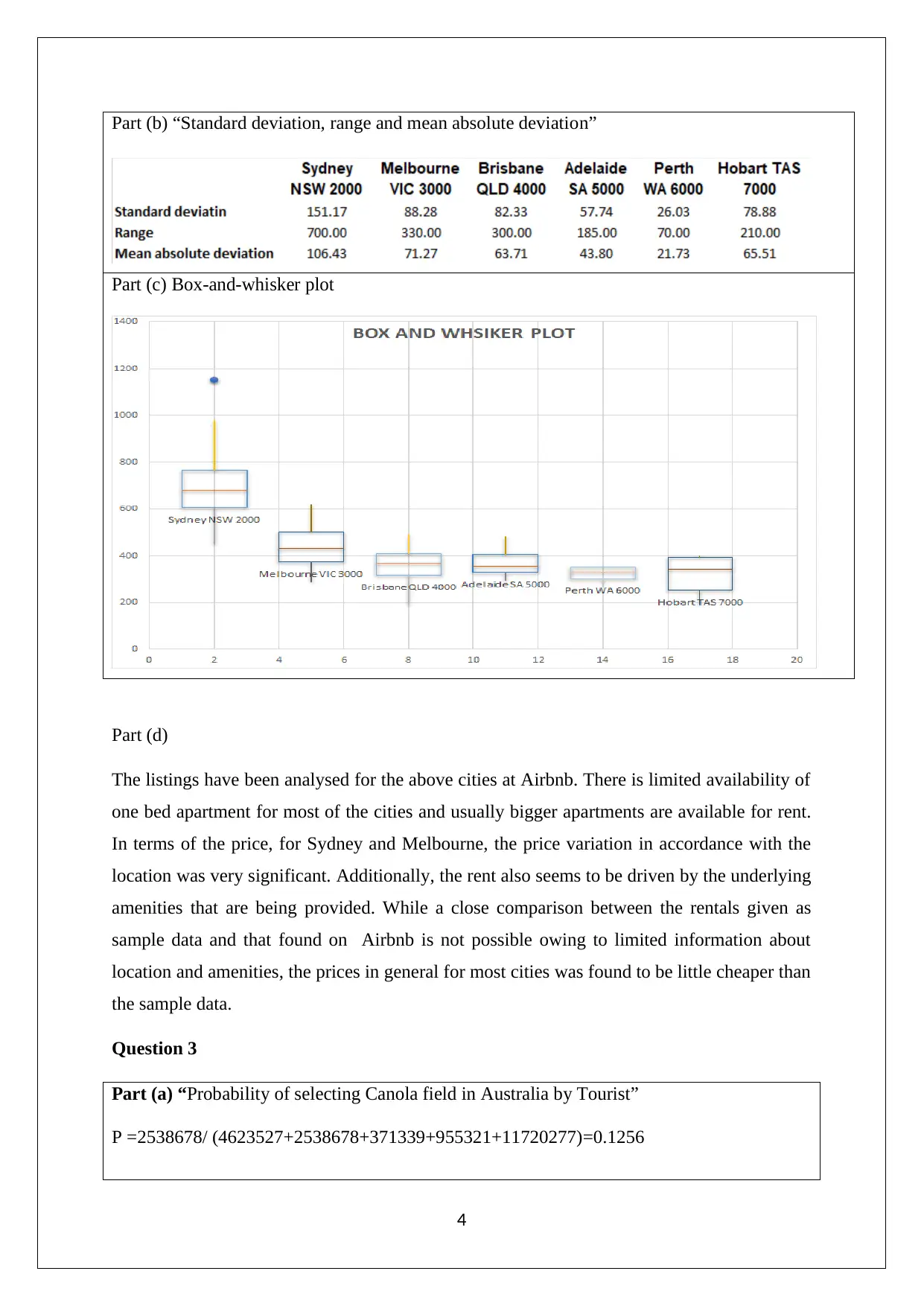
Part (b) “Standard deviation, range and mean absolute deviation”
Part (c) Box-and-whisker plot
Part (d)
The listings have been analysed for the above cities at Airbnb. There is limited availability of
one bed apartment for most of the cities and usually bigger apartments are available for rent.
In terms of the price, for Sydney and Melbourne, the price variation in accordance with the
location was very significant. Additionally, the rent also seems to be driven by the underlying
amenities that are being provided. While a close comparison between the rentals given as
sample data and that found on Airbnb is not possible owing to limited information about
location and amenities, the prices in general for most cities was found to be little cheaper than
the sample data.
Question 3
Part (a) “Probability of selecting Canola field in Australia by Tourist”
P =2538678/ (4623527+2538678+371339+955321+11720277)=0.1256
4
Part (c) Box-and-whisker plot
Part (d)
The listings have been analysed for the above cities at Airbnb. There is limited availability of
one bed apartment for most of the cities and usually bigger apartments are available for rent.
In terms of the price, for Sydney and Melbourne, the price variation in accordance with the
location was very significant. Additionally, the rent also seems to be driven by the underlying
amenities that are being provided. While a close comparison between the rentals given as
sample data and that found on Airbnb is not possible owing to limited information about
location and amenities, the prices in general for most cities was found to be little cheaper than
the sample data.
Question 3
Part (a) “Probability of selecting Canola field in Australia by Tourist”
P =2538678/ (4623527+2538678+371339+955321+11720277)=0.1256
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
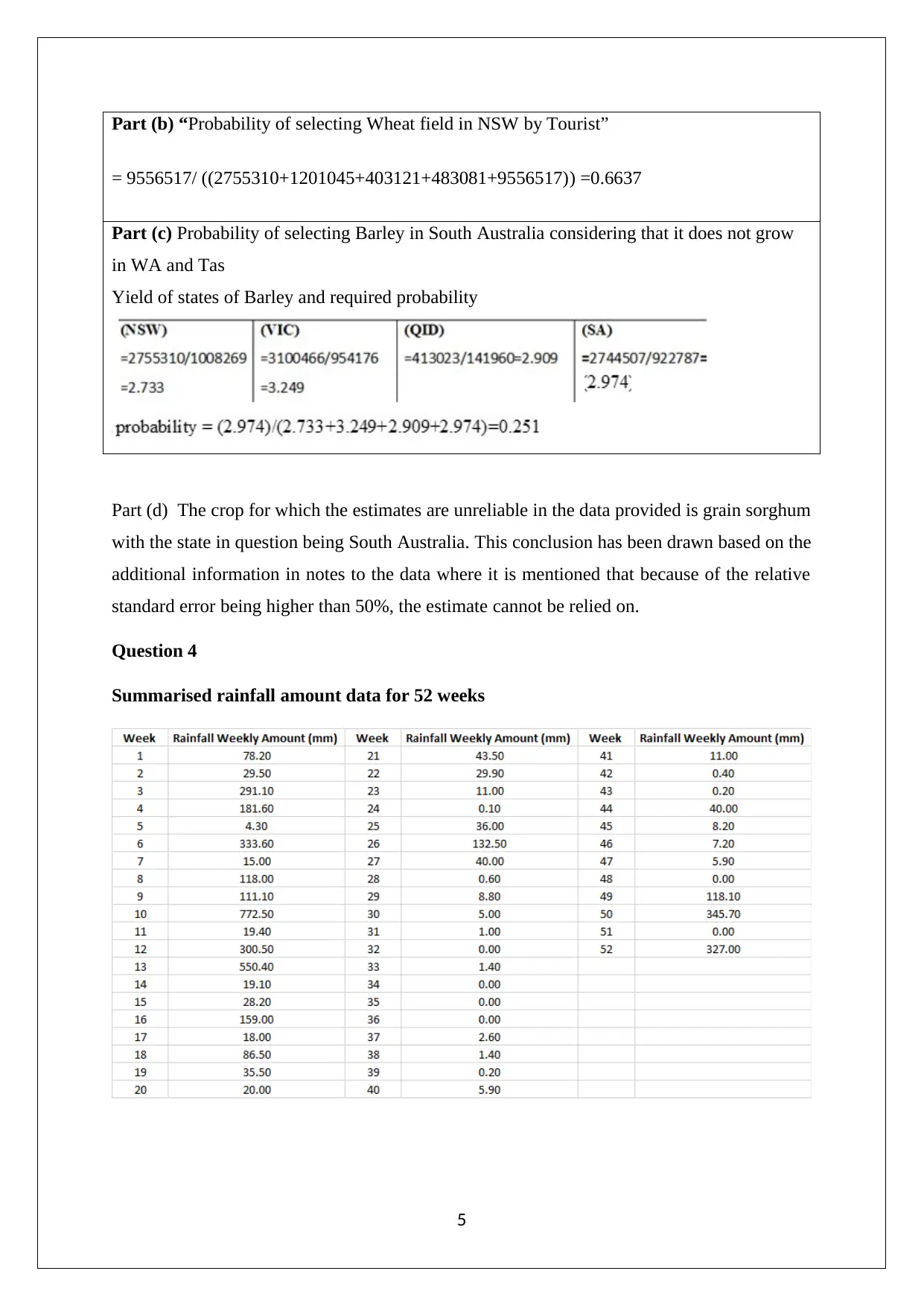
Part (b) “Probability of selecting Wheat field in NSW by Tourist”
= 9556517/ ((2755310+1201045+403121+483081+9556517)) =0.6637
Part (c) Probability of selecting Barley in South Australia considering that it does not grow
in WA and Tas
Yield of states of Barley and required probability
Part (d) The crop for which the estimates are unreliable in the data provided is grain sorghum
with the state in question being South Australia. This conclusion has been drawn based on the
additional information in notes to the data where it is mentioned that because of the relative
standard error being higher than 50%, the estimate cannot be relied on.
Question 4
Summarised rainfall amount data for 52 weeks
5
= 9556517/ ((2755310+1201045+403121+483081+9556517)) =0.6637
Part (c) Probability of selecting Barley in South Australia considering that it does not grow
in WA and Tas
Yield of states of Barley and required probability
Part (d) The crop for which the estimates are unreliable in the data provided is grain sorghum
with the state in question being South Australia. This conclusion has been drawn based on the
additional information in notes to the data where it is mentioned that because of the relative
standard error being higher than 50%, the estimate cannot be relied on.
Question 4
Summarised rainfall amount data for 52 weeks
5

Part (b) When rainfall follows Normal Distribution
(i) P (Rainfall would be between 10 mm and 15 mm)
Question 5
(a) The normal probability plots (NPP) for the given data i.e. four variables have been
obtained using Excel.
6
(i) P (Rainfall would be between 10 mm and 15 mm)
Question 5
(a) The normal probability plots (NPP) for the given data i.e. four variables have been
obtained using Excel.
6
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
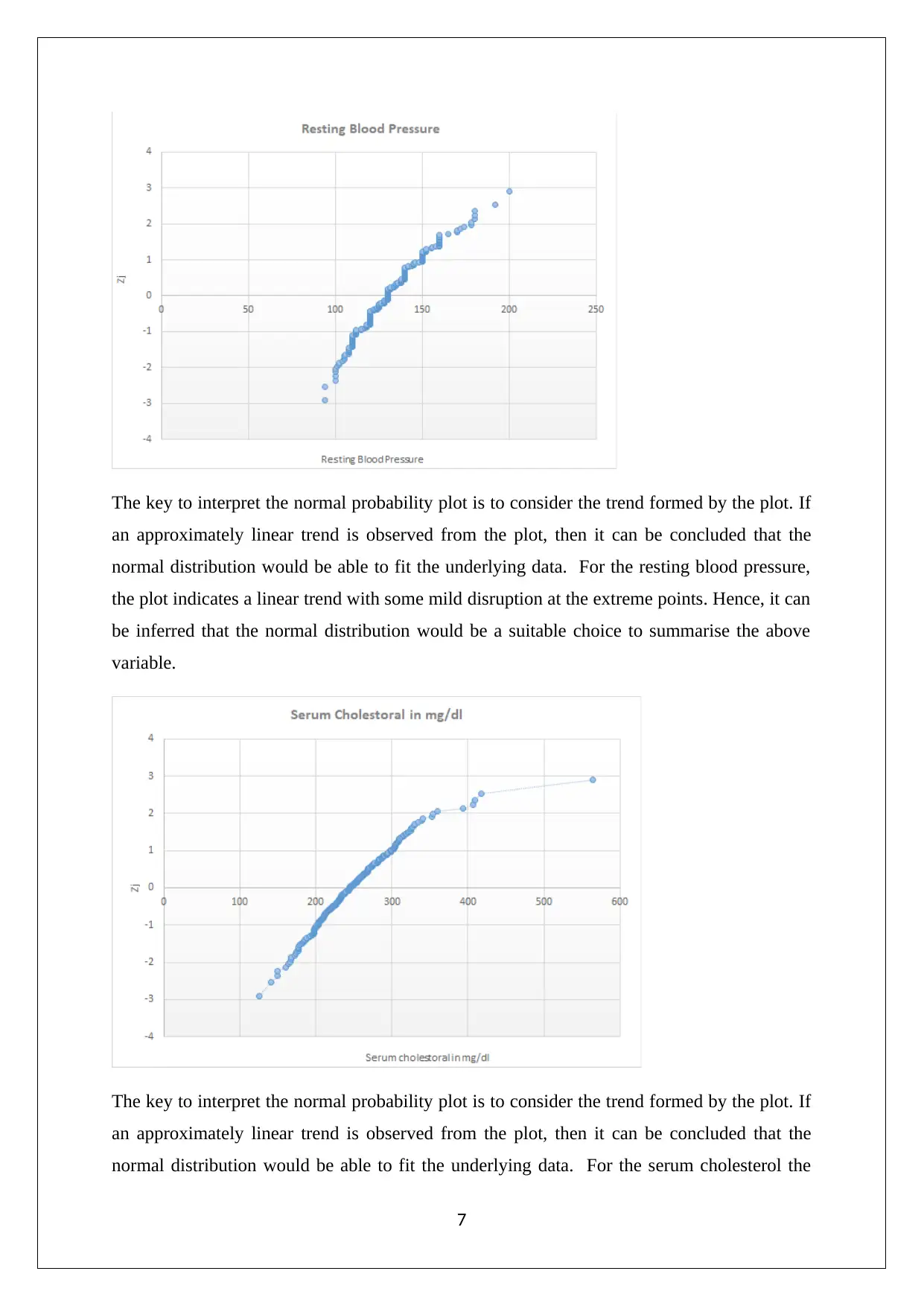
The key to interpret the normal probability plot is to consider the trend formed by the plot. If
an approximately linear trend is observed from the plot, then it can be concluded that the
normal distribution would be able to fit the underlying data. For the resting blood pressure,
the plot indicates a linear trend with some mild disruption at the extreme points. Hence, it can
be inferred that the normal distribution would be a suitable choice to summarise the above
variable.
The key to interpret the normal probability plot is to consider the trend formed by the plot. If
an approximately linear trend is observed from the plot, then it can be concluded that the
normal distribution would be able to fit the underlying data. For the serum cholesterol the
7
an approximately linear trend is observed from the plot, then it can be concluded that the
normal distribution would be able to fit the underlying data. For the resting blood pressure,
the plot indicates a linear trend with some mild disruption at the extreme points. Hence, it can
be inferred that the normal distribution would be a suitable choice to summarise the above
variable.
The key to interpret the normal probability plot is to consider the trend formed by the plot. If
an approximately linear trend is observed from the plot, then it can be concluded that the
normal distribution would be able to fit the underlying data. For the serum cholesterol the
7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
plot indicates a linear trend with some mild disruption at the extreme points. Hence, it can be
inferred that the normal distribution would be a suitable choice to summarise the above
variable.
The key to interpret the normal probability plot is to consider the trend formed by the plot. If
an approximately linear trend is observed from the plot, then it can be concluded that the
normal distribution would be able to fit the underlying data. For the maximum heart rate
achieved the plot indicates a linear trend with some mild disruption at the extreme points.
Hence, it can be inferred that the normal distribution would be a suitable choice to summarise
the above variable.
8
inferred that the normal distribution would be a suitable choice to summarise the above
variable.
The key to interpret the normal probability plot is to consider the trend formed by the plot. If
an approximately linear trend is observed from the plot, then it can be concluded that the
normal distribution would be able to fit the underlying data. For the maximum heart rate
achieved the plot indicates a linear trend with some mild disruption at the extreme points.
Hence, it can be inferred that the normal distribution would be a suitable choice to summarise
the above variable.
8
The key to interpret the normal probability plot is to consider the trend formed by the plot. If
an approximately linear trend is observed from the plot, then it can be concluded that the
normal distribution would be able to fit the underlying data. For the oldpeak variable the plot
indicates a linear trend with some mild disruption at the extreme points. Hence, it can be
inferred that the normal distribution would be a suitable choice to summarise the above
variable.
(b) The confidence interval for the given four variables have been computed using Excel..
9
an approximately linear trend is observed from the plot, then it can be concluded that the
normal distribution would be able to fit the underlying data. For the oldpeak variable the plot
indicates a linear trend with some mild disruption at the extreme points. Hence, it can be
inferred that the normal distribution would be a suitable choice to summarise the above
variable.
(b) The confidence interval for the given four variables have been computed using Excel..
9
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

The objective is to identify any of the four variables listed above to identify if the patient is
suffering from heart disease or not. As a result, the only useful variables would be those
where the confidence intervals for the two categories of patient are separate and display no
overlapping. As a result, for such cases based on the underlying value of the variable, it can
be determined with reasonable precision as to whether the patient has heart disease or not.
There are three variables where no overlapping of intervals is observed. These are listed
below.
Resting blood pressure
Maximum heart rate achieved
Oldpeak
It is noteworthy that serum cholesterol cannot be used for differentiating between patients as
some values such as 250 exist in both intervals and hence conclusion cannot be drawn about
the prevalence of heart disease.
10
suffering from heart disease or not. As a result, the only useful variables would be those
where the confidence intervals for the two categories of patient are separate and display no
overlapping. As a result, for such cases based on the underlying value of the variable, it can
be determined with reasonable precision as to whether the patient has heart disease or not.
There are three variables where no overlapping of intervals is observed. These are listed
below.
Resting blood pressure
Maximum heart rate achieved
Oldpeak
It is noteworthy that serum cholesterol cannot be used for differentiating between patients as
some values such as 250 exist in both intervals and hence conclusion cannot be drawn about
the prevalence of heart disease.
10
1 out of 10
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




