Statistics in Practice
Added on 2022-11-28
14 Pages1201 Words305 Views
STATISTICS IN
PRACTICE
STUDENT ID:
[Pick the date]
PRACTICE
STUDENT ID:
[Pick the date]

Question 1
Variable Name Type
Gender Categorical Nominal
Age Numerical Discrete
Ethnicity Categorical Nominal
Marital Categorical Nominal
Qualification Categorical Nominal
PostSchool Categorical Nominal
Hours Numerical Discrete
Income Numerical Discrete
Question 2
(a) Histogram of weekly income
2
Variable Name Type
Gender Categorical Nominal
Age Numerical Discrete
Ethnicity Categorical Nominal
Marital Categorical Nominal
Qualification Categorical Nominal
PostSchool Categorical Nominal
Hours Numerical Discrete
Income Numerical Discrete
Question 2
(a) Histogram of weekly income
2

11 to 233 233 to
456
456 to
678
678 to
900
900 to
1122
1122 to
1345
1345 to
1567
1567 to
1789
0.0
10.0
20.0
30.0
40.0
50.0
60.0 Histogram : Weekly Income
Weekly Income ($)
Frequency
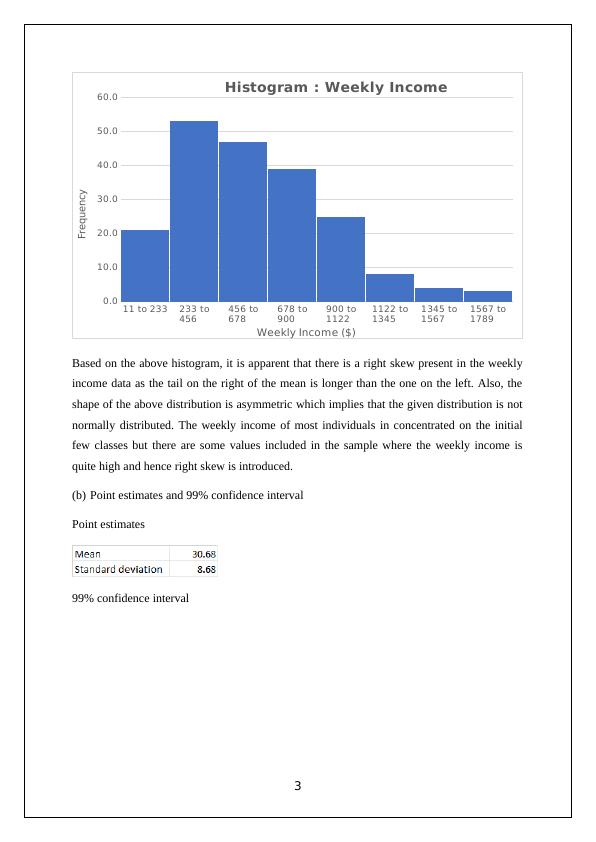
Based on the above histogram, it is apparent that there is a right skew present in the weekly
income data as the tail on the right of the mean is longer than the one on the left. Also, the
shape of the above distribution is asymmetric which implies that the given distribution is not
normally distributed. The weekly income of most individuals in concentrated on the initial
few classes but there are some values included in the sample where the weekly income is
quite high and hence right skew is introduced.
(b) Point estimates and 99% confidence interval
Point estimates
99% confidence interval
3
456
456 to
678
678 to
900
900 to
1122
1122 to
1345
1345 to
1567
1567 to
1789
0.0
10.0
20.0
30.0
40.0
50.0
60.0 Histogram : Weekly Income
Weekly Income ($)
Frequency
Based on the above histogram, it is apparent that there is a right skew present in the weekly
income data as the tail on the right of the mean is longer than the one on the left. Also, the
shape of the above distribution is asymmetric which implies that the given distribution is not
normally distributed. The weekly income of most individuals in concentrated on the initial
few classes but there are some values included in the sample where the weekly income is
quite high and hence right skew is introduced.
(b) Point estimates and 99% confidence interval
Point estimates
99% confidence interval
3
(c) The appropriate general distribution of the variable X would be student t with mean =
30.68 and standard deviation = 8.68.
The given distribution is suitable considering that the data is skewed owing to which a
normal distribution is not appropriate for capturing the continuous variable X.
(d) The relevant hypothesis test for evaluating the claim that the mean weekly income in
Australia in 2007 was NZD 986. The relevant hypothesis test has been performed in
Excel and the requisite output is indicated below. Considering that population standard
deviation is not known, hence the relevant test statistic is t
T value = (Sample mean – Hypothesised mean)/Standard Error
4
30.68 and standard deviation = 8.68.
The given distribution is suitable considering that the data is skewed owing to which a
normal distribution is not appropriate for capturing the continuous variable X.
(d) The relevant hypothesis test for evaluating the claim that the mean weekly income in
Australia in 2007 was NZD 986. The relevant hypothesis test has been performed in
Excel and the requisite output is indicated below. Considering that population standard
deviation is not known, hence the relevant test statistic is t
T value = (Sample mean – Hypothesised mean)/Standard Error
4

End of preview
Want to access all the pages? Upload your documents or become a member.
Related Documents
STAT 193: Statistics in Practice Project Assignmentlg...
|8
|1723
|272
