Statistics Assignment: Regression, Forecasting, and Linear Programming

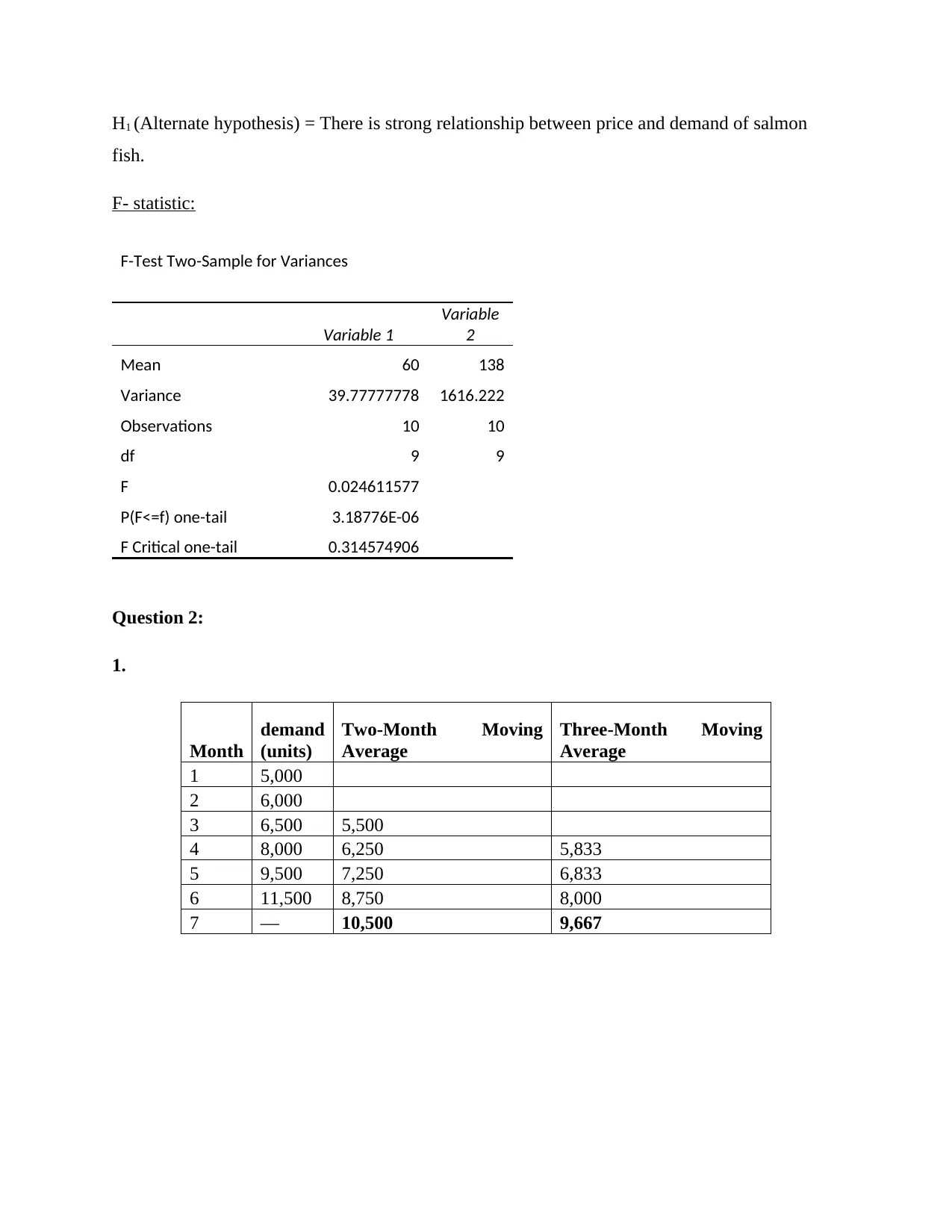
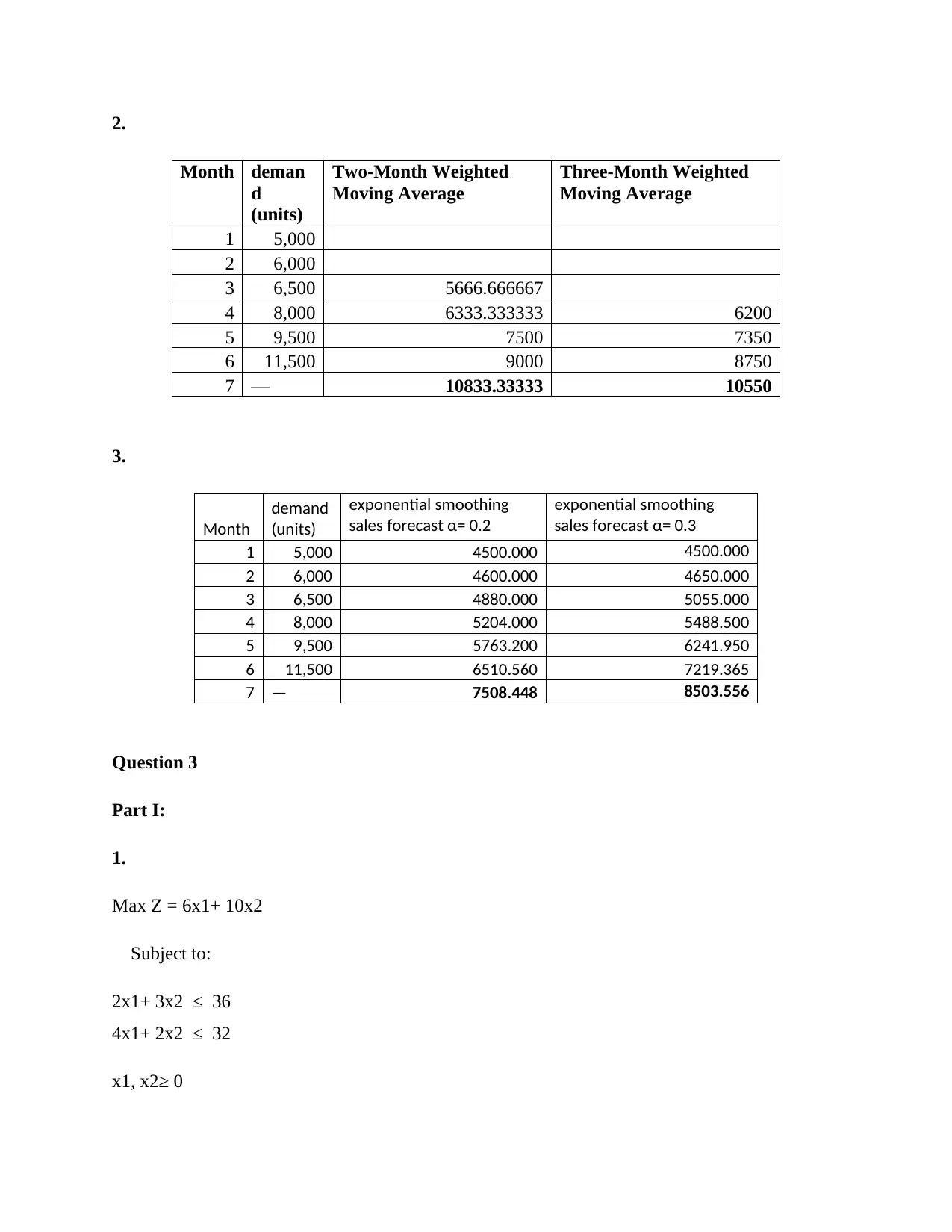
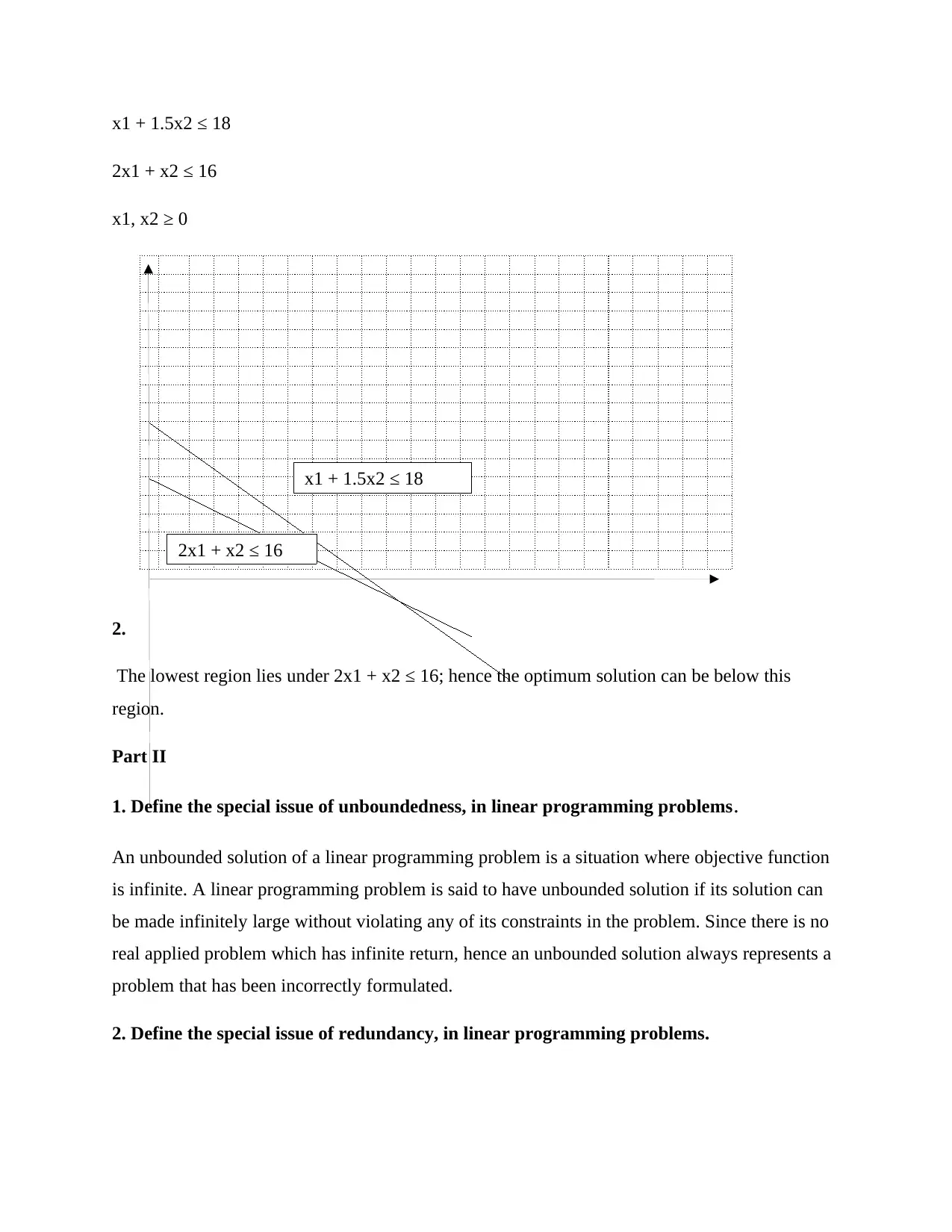
This statistics assignment provides solutions to problems covering several key areas. Question 1 focuses on regression analysis, including interpreting scatter diagrams, calculating regression equations, predicting values, interpreting R-squared, and hypothesis testing using the F-statistic. Question 2 explores forecasting techniques, including moving averages and exponential smoothing, to predict demand. Question 3 delves into linear programming, involving problem formulation, solving using graphical methods, and addressing special issues like unboundedness and redundancy. Finally, Question 4 addresses a minimum path problem. The solutions provide detailed calculations and interpretations for each problem, offering a comprehensive understanding of statistical concepts and their applications.

Statistics Q1

Question 1:
1.
The scatter diagram shows the negative relationship between X and Y; which means if X
increases; Y will decrease and vice a versa.
2.
Sum of X = 600
Sum of Y = 1380
Mean X = 60
Mean Y = 138
Sum of squares (SSX) = 358
Sum of products (SP) = -2151
Regression Equation = ŷ = bX + a
b = SP/SSX = -2151/358 = -6.00838
a = MY - bMX = 138 - (-6.01*60) = 498.50279
ŷ = -6.00838X + 498.50279
3.
ŷ = -6.00838X + 498.50279
ŷ = -6.00838(70) + 498.50279 = 77.91619
4.
Here R2 = 0.8885
Interpretation: The result shows that there is near to perfect relationship between both variable
x and y. This is a strong negative correlation, which means that high X variable scores go with
low Y variable scores (and vice versa).
5.
H0 (Null hypothesis) = There is no association between price of salmon fish and demand.

H1 (Alternate hypothesis) = There is strong relationship between price and demand of salmon
fish.
F- statistic:
F-Test Two-Sample for Variances
Variable 1
Variable
2
Mean 60 138
Variance 39.77777778 1616.222
Observations 10 10
df 9 9
F 0.024611577
P(F<=f) one-tail 3.18776E-06
F Critical one-tail 0.314574906
Question 2:
1.
Month
demand
(units)
Two-Month Moving
Average
Three-Month Moving
Average
1 5,000
2 6,000
3 6,500 5,500
4 8,000 6,250 5,833
5 9,500 7,250 6,833
6 11,500 8,750 8,000
7 — 10,500 9,667

2.
Month deman
d
(units)
Two-Month Weighted
Moving Average
Three-Month Weighted
Moving Average
1 5,000
2 6,000
3 6,500 5666.666667
4 8,000 6333.333333 6200
5 9,500 7500 7350
6 11,500 9000 8750
7 — 10833.33333 10550
3.
Month
demand
(units)
exponential smoothing
sales forecast α= 0.2
exponential smoothing
sales forecast α= 0.3
1 5,000 4500.000 4500.000
2 6,000 4600.000 4650.000
3 6,500 4880.000 5055.000
4 8,000 5204.000 5488.500
5 9,500 5763.200 6241.950
6 11,500 6510.560 7219.365
7 — 7508.448 8503.556
Question 3
Part I:
1.
Max Z = 6x1+ 10x2
Subject to:
2x1+ 3x2 ≤ 36
4x1+ 2x2 ≤ 32
x1, x2≥ 0

x1 + 1.5x2 ≤ 18
2x1 + x2 ≤ 16
x1, x2 ≥ 0
2.
The lowest region lies under 2x1 + x2 ≤ 16; hence the optimum solution can be below this
region.
Part II
1. Define the special issue of unboundedness, in linear programming problems.
An unbounded solution of a linear programming problem is a situation where objective function
is infinite. A linear programming problem is said to have unbounded solution if its solution can
be made infinitely large without violating any of its constraints in the problem. Since there is no
real applied problem which has infinite return, hence an unbounded solution always represents a
problem that has been incorrectly formulated.
2. Define the special issue of redundancy, in linear programming problems.
x1 + 1.5x2 ≤ 18
2x1 + x2 ≤ 16

A redundant constraint is a constraint that can be removed from a system of linear constraints
without changing the feasible region.
Question 4
1.
Minimum path = A + B + C + D + E + I + F + G + H
2.
Minimum total distance = 2 + 4 + 2 + 1 + 2 + 5 + 1 + 3
= 20
3.
Other types of service connections:
 Electricity line
 Internet connections through fiber cable
 TV cable
 Computer interconnections
 Road manufacturing