Statistics Assignment: Analyzing Hotel Review Data from TripAdvisor
VerifiedAdded on 2023/04/21
|7
|1102
|153
Homework Assignment
AI Summary
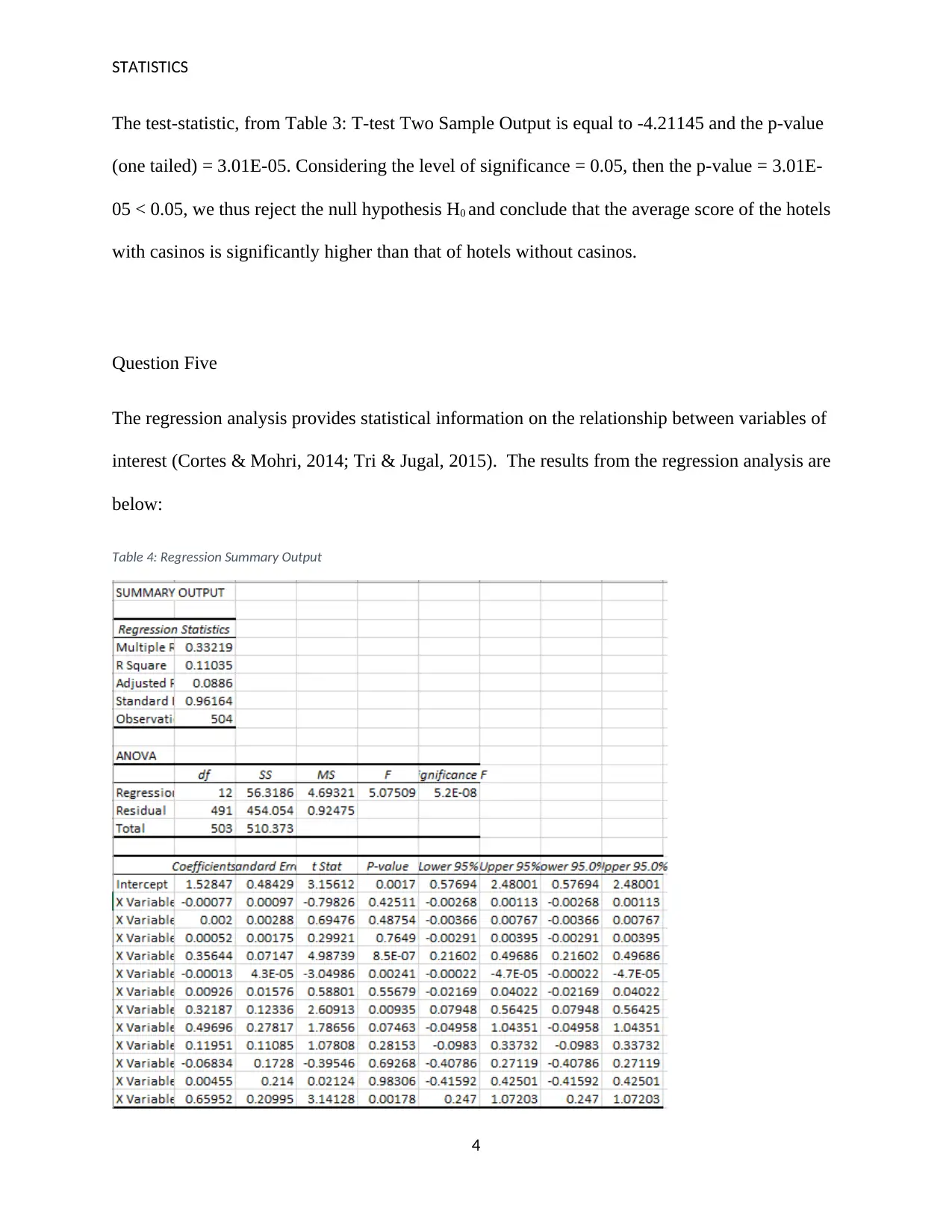
This statistics assignment analyzes a dataset of TripAdvisor hotel reviews, focusing on predicting hotel scores based on various factors. The analysis begins with descriptive statistics, including mean, median, standard deviation, and outlier identification for variables like score, hotel stars, member years, and the number of reviews. A scatterplot and correlation analysis explore the relationship between the number of hotel reviews and helpful votes, revealing a positive correlation. Furthermore, the assignment utilizes a t-test to compare the average scores of hotels with and without casinos, leading to the rejection of the null hypothesis. Regression analysis is then employed to determine the impact of variables such as number of reviews, hotel stars, and helpful votes on the score, with the regression model explaining a small percentage of the variance. Finally, logistic regression is used to analyze the data, examining the relationship between the variables, such as number of rooms and casino presence, and the score, providing insights into how these factors influence hotel ratings.
1 out of 7












![[object Object]](/_next/static/media/star-bottom.7253800d.svg)