Statistics Homework: Hypothesis Testing and Mean Earnings Comparison
VerifiedAdded on 2023/01/17
|5
|708
|36
Homework Assignment
AI Summary
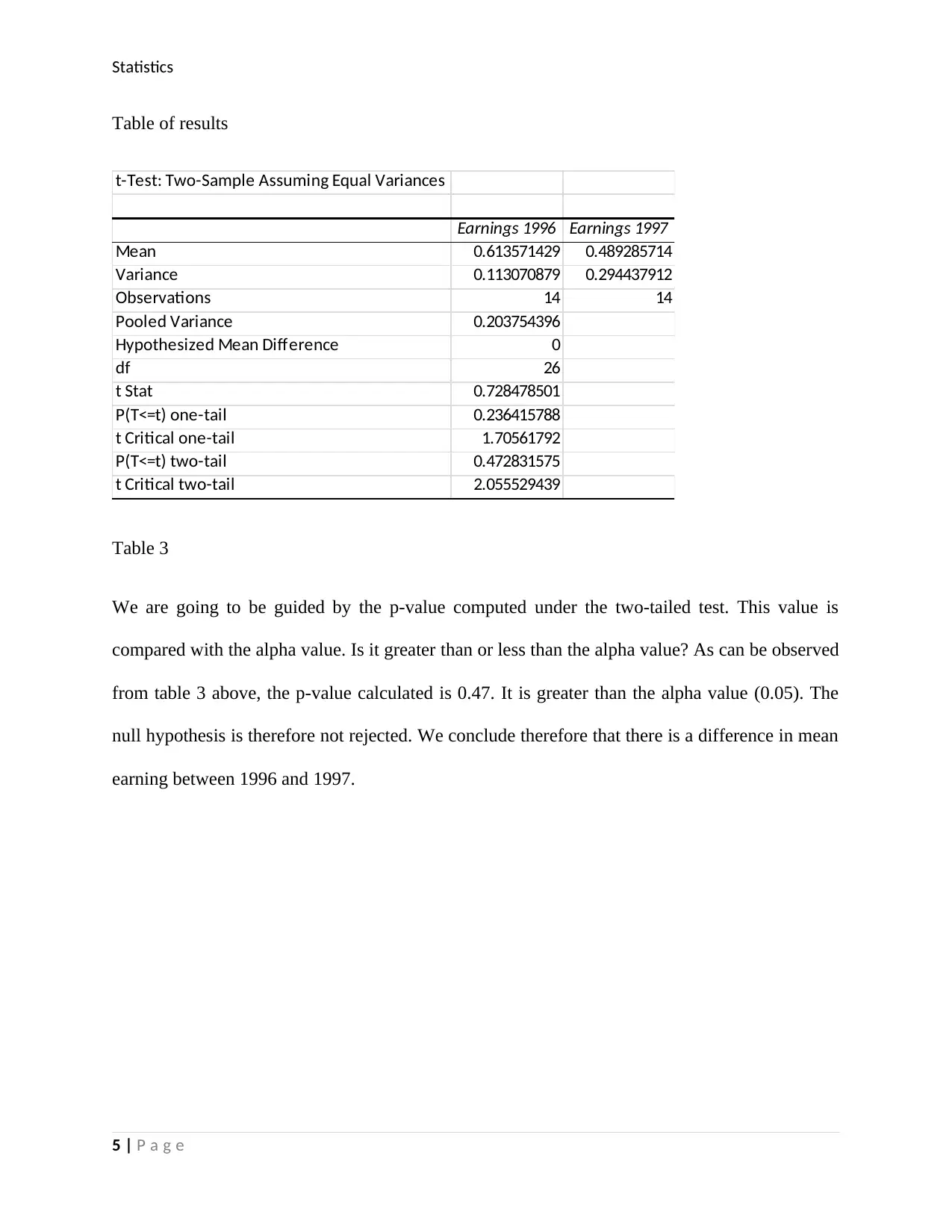
This statistics homework assignment presents solutions to two problems involving hypothesis testing. The first problem focuses on comparing the variability of waiting times in two different banks using a Levene's test and then comparing the means using a pooled-variance t-test, concluding that there is a significant difference in mean waiting times. The second problem examines the difference in mean earnings between 1996 and 1997, employing a two-sample t-test assuming equal variances. The analysis concludes that there is no significant difference in mean earnings between the two years. The assignment provides detailed tables and p-value analysis to support the conclusions drawn from the statistical tests.
1 out of 5











![[object Object]](/_next/static/media/star-bottom.7253800d.svg)