Calculations and Interpretation of Stock Returns and CAPM Model

This document provides calculations and interpretation of stock returns and CAPM model. It includes hypothesis testing, comparison of variances, and linear regression analysis. The document also discusses the distribution of residuals and the assumptions of simple linear regression.

STATISTICS
STUDENT NAME/ID
[Pick the date]

PART A: CALCULATIONS
TASK B
(1) The stock return (i.e. Boeing and General Dynamics) along with index return has been
calculated in accordance with the formula outlined. The underlying result is shown below.
1

It needs to be ascertained if the distribution corresponding to the returns for the two stocks (i.e.
BA and GD) is normal or not with the application of Jarque Bera test. The relevant hypotheses to
facilitate this test are illustrated as follows.
H0 (Null Hypothesis): For the underlying stock, the distribution is not different from normal
distribution in a statistically significant manner.
H1 (Alternative Hypothesis): For the underlying stock, the distribution is different from normal
distribution in a statistically significant manner.
α or significance level assumed for the test is 5%.
The test statistics of relevance would be JB statistic which may be computed using the formula
illustrated below.
The key inputs for the computation of JB statistic is in the form of skew and kurtosis pertaining
to the underlying returns of the stock. The underlying JB test statistic for the two stocks whose
distribution is being tested is exhibited below.
The corresponding critical value of JB statistic is 9.87.
Since JB test statistic for each of two stocks > critical, hence the available evidence warrants
rejection of H0 in favour of H1. It would be fair to draw the conclusion that distribution of returns
for both Boeing and General Dynamics tend to deviate from normal distribution and thereby
cannot be assumed as normal.
2

(2) Owing to the non-normal distribution of the stock returns for General Dynamics coupled
with non-availability of population standard deviation, the test statistics for conducting
hypothesis is t. Requisite hypotheses to facilitate the test are highlighted below.
α or significance level assumed for the test is 5%.
As indicated above, the relevant test statistic for the hypothesis test is t based on the underlying
student t distribution. The one sample two tail test has been performed with the aid of excel
thereby leading to the following output.
In accordance with hypothesis testing based on p value, the null hypothesis would be rejected
only when the p value is not greater than the significance level taken for the hypothesis test. This
condition is satisfied here which would imply that H0 would face rejection while H1 would be
accepted.
(3) In order to determine whether the risk associated with the two stocks is significantly different
or not, the hypothesis test has been performed for comparison of variances.
α or significance level assumed for the test is 5%.
3

The relevant test statistics for comparison of variances is F and this test has been performed
based on the inbuilt option available under “Data Analysis’ tab in Excel. The output using the
returns of the two stocks is summarised as follows.
In accordance with hypothesis testing based on p value, the null hypothesis would be rejected
only when the p value is not greater than the significance level taken for the hypothesis test. As
the given hypothesis test is two tail, hence the appropriate p value would be twice that of the
highlighted value i.e. 0.016*2 = 0.032
The comparison of the above p value with the level of significance clearly yields that the
available evidence would lead to the conclusion that H0 would face rejection while H1 would be
accepted.
(4) The hypothesis test to aid the comparison of the average returns of the Boeing and General
Dynamic stock is shown below.
α or significance level assumed for the test is 5%.
Instead of the t statistic based approach for comparison of means, the given hypothesis test is to
be performed using the confidence interval approach. In this approach, the key computation to
perform relates to determining the 95% confidence interval for mean returns corresponding to
both the stocks.
4

.
The decision rule is that H0 would be rejected only when there is no common value in the two
confidence intervals. This is clearly not the case here and hence the evidence at hand does not
hint at H0 rejection. Therefore, H1 cannot be accepted. The preferable stock is General Dynamic
as there is no significant difference in returns but in terms of risk GD has lower risk in
comparison of Boeing (BA).
TASK C
(5) For the estimation of CAPM model, the independent variables is the excess return related to
S&P 500 index while the dependent variable is the excess return related to preferable stock
(General Dynamics). The output from Excel in relation to the linear regression model is
stated below.
5

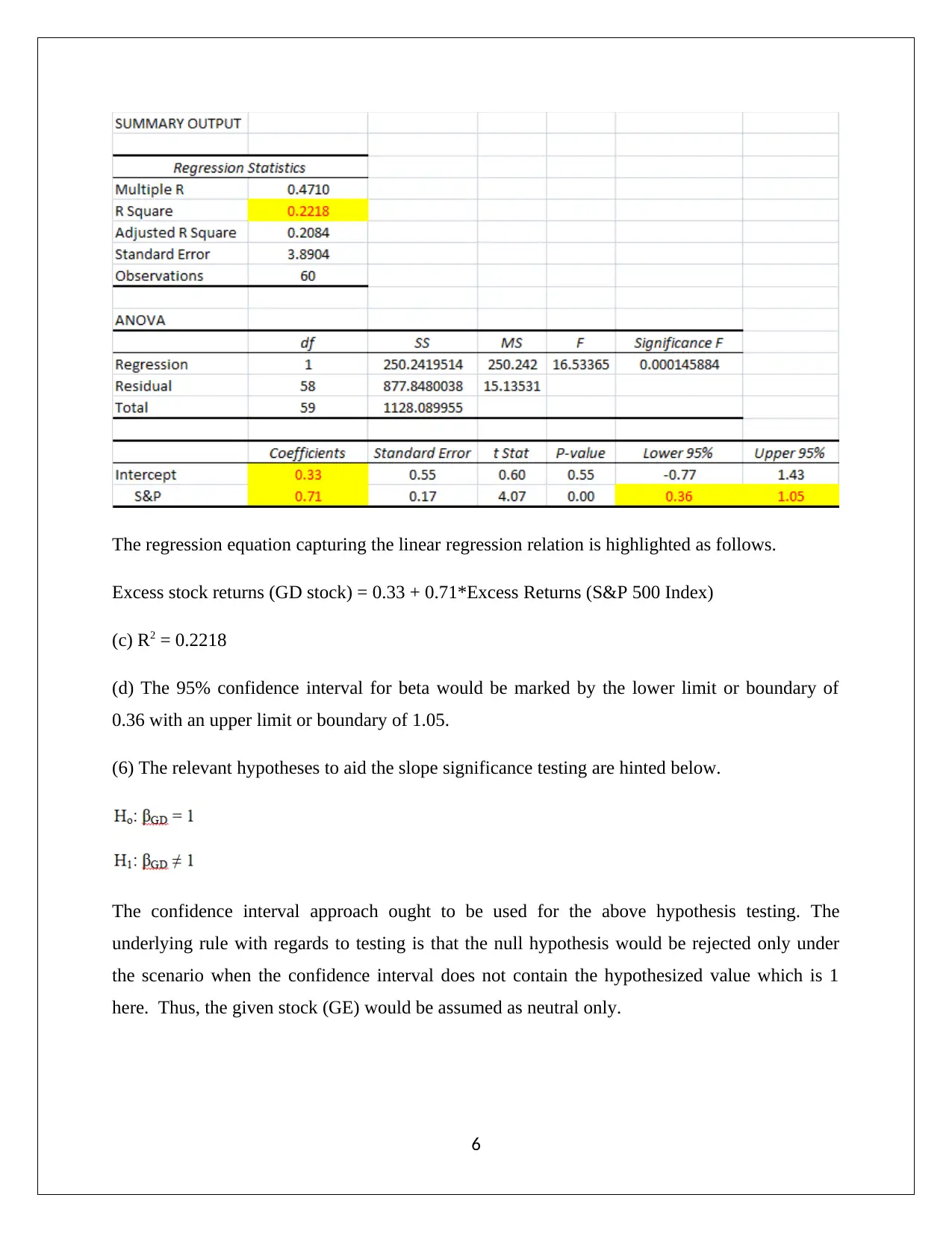
The regression equation capturing the linear regression relation is highlighted as follows.
Excess stock returns (GD stock) = 0.33 + 0.71*Excess Returns (S&P 500 Index)
(c) R2 = 0.2218
(d) The 95% confidence interval for beta would be marked by the lower limit or boundary of
0.36 with an upper limit or boundary of 1.05.
(6) The relevant hypotheses to aid the slope significance testing are hinted below.
The confidence interval approach ought to be used for the above hypothesis testing. The
underlying rule with regards to testing is that the null hypothesis would be rejected only under
the scenario when the confidence interval does not contain the hypothesized value which is 1
here. Thus, the given stock (GE) would be assumed as neutral only.
6

(7) A key assumption for simple linear regression is that the residuals must be normal in their
distribution. This has been put to test based on the hypothesis test which uses the Jarque Bera
test. The relevant hypotheses to facilitate this test are illustrated as follows.
H0 (Null Hypothesis): For the underlying residuals, the distribution is not different from normal
distribution in a statistically significant manner.
H1 (Alternative Hypothesis): For the underlying residuals, the distribution is different from
normal distribution in a statistically significant manner.
α or significance level assumed for the test is 5%.
The test statistics of relevance would be JB statistic which may be computed using the formula
The key inputs for the computation of JB statistic is in the form of skew and kurtosis pertaining
to the variable under consideration. The underlying JB test statistic for the residual whose
distribution is being tested is exhibited below.
JB test statistic < critical value (9.87) and hence H0 cannot be rejected. This implies that the
assumption about normal distribution of residuals is true.
7

PART B: Interpretation
(1) The JB test statistic based hypothesis test was performed for the returns of both stocks and
neither of the stock returns was indicated to be normally distributed. This is apparent from
the rejection of null hypothesis.
(2) The two tail t based hypothesis test provides clear evident in relation to GD stock average
return being significantly different from the hypothesised value of 2.8%.
(3) As the null hypothesis has been rejected, hence it would be correct to draw the conclusion
that variances for the returns of BA and GD stocks tend to differ. Based on the sample
variance comparison, it would be fair to say that returns of GD stock have less variance in
comparison to BA stock returns thereby implying lower risk for the investor.
(4) As the null hypothesis cannot be rejected, hence there is no significant difference with
regards to the average returns for BA and GD. Investors normally prefer a stock which provides
higher returns with lower risk. In this case, based on returns, no stock can be preferred over the
other. However, lower risk (denoted by variance of returns) is observed for GD stock in
comparison to BA stock. As a result, superior stock has been identified as GD.
(5) (b) The CAPM model output from Excel highlights the beta value of GD as 0.71. This would
imply that as the excess returns on S&P 500 index witnesses a change of 1%, the GD stock
excess returns would be expected to witness a change of 0.71%. Both the stock (GD) and index
excess returns would move in the same direction.
(c) The R2 value implies that the given regression model is capable of explaining only 22.18% of
the changes observed in excess returns related to GD stock which is quite less. This clearly
indicates that instead of CAPM model, multi-factor models which use multiple variables for
capturing risk would be more favourable.
(d) We can concluded with 95% confidence that the beta value of General Dynamic stock would
lie between the lower bound of 0.36 and higher bound of 1.05.
8

(6) With regards to hypothesis testing using the confidence interval approach, the available
evidence suggests that the GD stock can be assumed to be neutral as the beta value does not
differ significantly from 1.
(7) The residuals of the CAPM model have been found to be normally distributed which augers
well for the validity of the model as this is one of the key assumptions accompanying simple
linear regression.
9