Statistics Coursework: T-Test Analysis of Gender Score Differences

This statistics assignment demonstrates a two-sample t-test with unequal variances to compare the average scores of male and female students. The analysis begins by stating the assumptions of the t-test and defining the null and alternative hypotheses. Given sample means, standard deviatio...Read More

Running Head: STATISTICS
Statistics
Name of the student:
Name of the university:
Course ID:

STATISTICS 1
Table of Contents
Answers:..........................................................................................................................................2
Answer 1......................................................................................................................................2
Part A........................................................................................................................................2
Part B........................................................................................................................................4
References:......................................................................................................................................5

2STATISTICS
Answers:
Answer 1.
Part A
Assumptions:
The t-test for two population means corresponds a right-tailed tests. The two samples are needed
to be independent with each other (Boneau 1960).
Provided description:
The given problem indicates that the mean (X 1) = 82 and ( X 2) = 81. On the other hand,
standard deviations of two samples are- S1= 6 and S2= 4. The sample sizes of two different data
sets are- n1= 252 and n2= 150.
Test applied:
Two sample t-test with known and unequal variances. The t-test is one-tailed.
Hypotheses:
Null hypothesis (H0): The averages of scores of male and female students are equal to each other
(μ1= μ2).
Alternative hypothesis (H0): The average score of female students is greater than the average
score of male students (μ1> μ2).
Region of rejection:
On the basis of provided information, the significance level is assumed to be α= 5%.
The rejection region for this right-tailed test is R = {α: α<0.05} = {t: t>tcrit}.
Test statistic:
The t-statistic of population variances is computed as-

3STATISTICS
Here, t =
(82−81)
√( 62
252 + 42
150 ) = 2.001907.
Degrees of freedom:
The degrees of freedom of t-statistic with unequal variances is calculated by the formula-
Calculated degrees of freedom =
( 62
252 + 42
150 )
2
1
(252−1)∗( 62
252 )
2
+ 1
(150−1)∗( 42
150 )
2 = 394.893.
Decision-making:
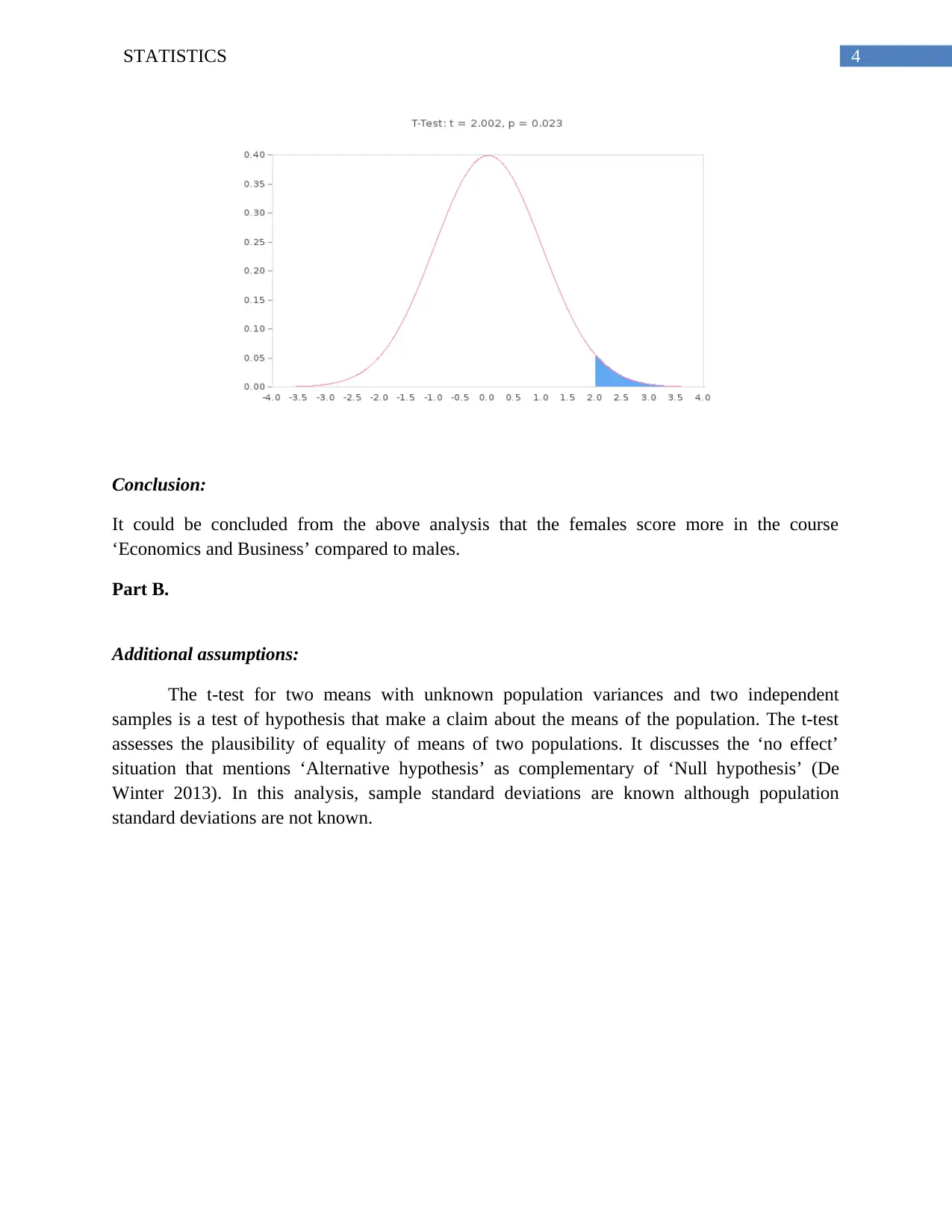
 The calculated p-value of the test-statistic (tcal = 2.001907) = 0.02299. As, 0.2299<0.05,
therefore, αcal< αcrit. Hence, the null hypothesis is rejected using p-value approach.
 Also, tcrit = T (0.95, 394.893) = 1.64873. As, 2.001907>1.64873, therefore, tcal>tcrit.
Hence, the null hypothesis is rejected using t-statistic approach (Romano and Lehmann
2005).
Interpretation:
It could be concluded that the null hypothesis (H0) is rejected at 5% level of significance. It is the
reason to say that there exists enough evidence to claim that population mean (μ1) is greater than
the other population mean (μ2) with 95% possibility.
Graphical presentation:

4STATISTICS
Conclusion:
It could be concluded from the above analysis that the females score more in the course
‘Economics and Business’ compared to males.
Part B.
Additional assumptions:
The t-test for two means with unknown population variances and two independent
samples is a test of hypothesis that make a claim about the means of the population. The t-test
assesses the plausibility of equality of means of two populations. It discusses the ‘no effect’
situation that mentions ‘Alternative hypothesis’ as complementary of ‘Null hypothesis’ (De
Winter 2013). In this analysis, sample standard deviations are known although population
standard deviations are not known.

5STATISTICS
References:
Boneau, C.A., 1960. The effects of violations of assumptions underlying the t test. Psychological
bulletin, 57(1), p.49.
De Winter, J.C., 2013. Using the Student's t-test with extremely small sample sizes. Practical
Assessment, Research & Evaluation, 18(10).
Romano, J.P. and Lehmann, E.L., 2005. Testing statistical hypotheses.