Structural Dynamics and Earthquake Engineering Assignment

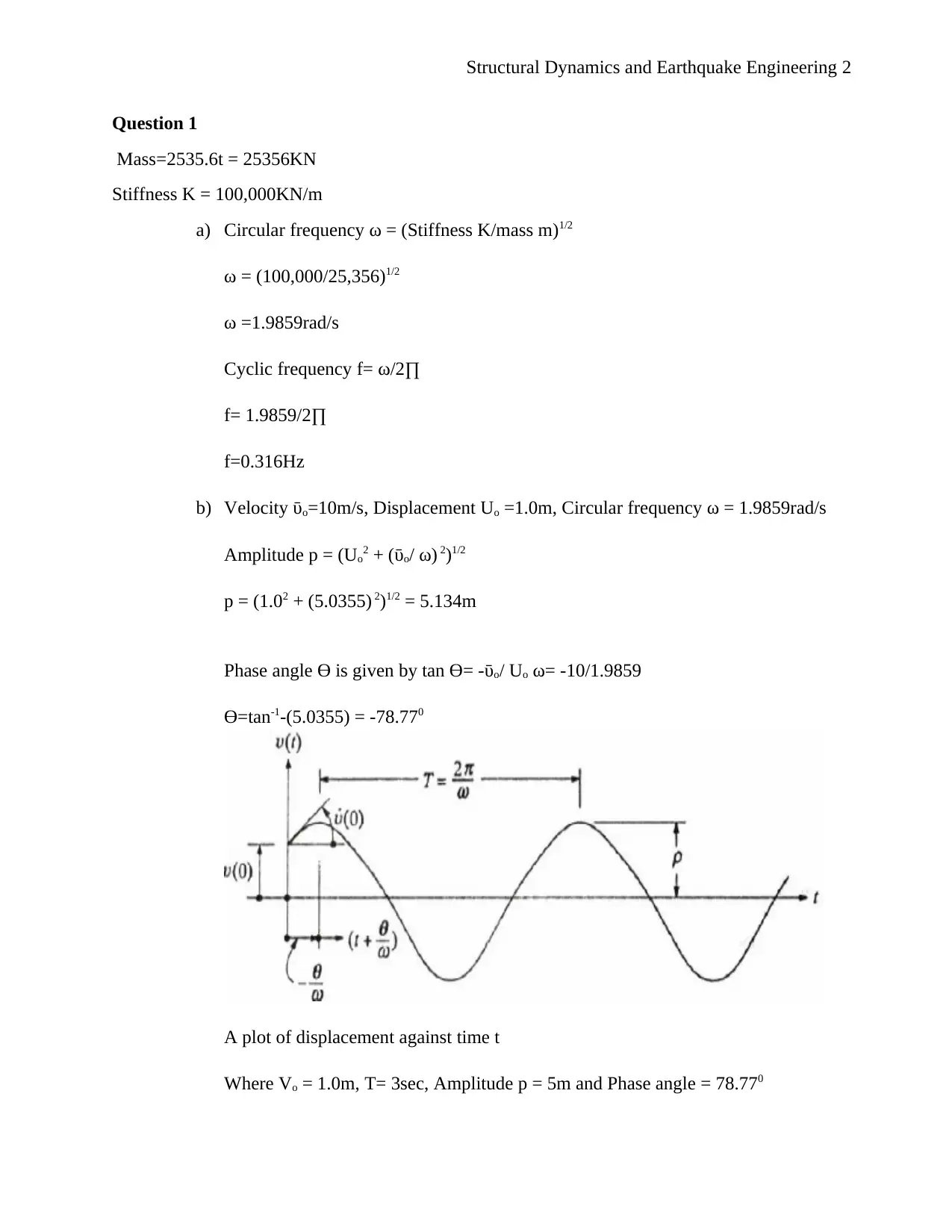
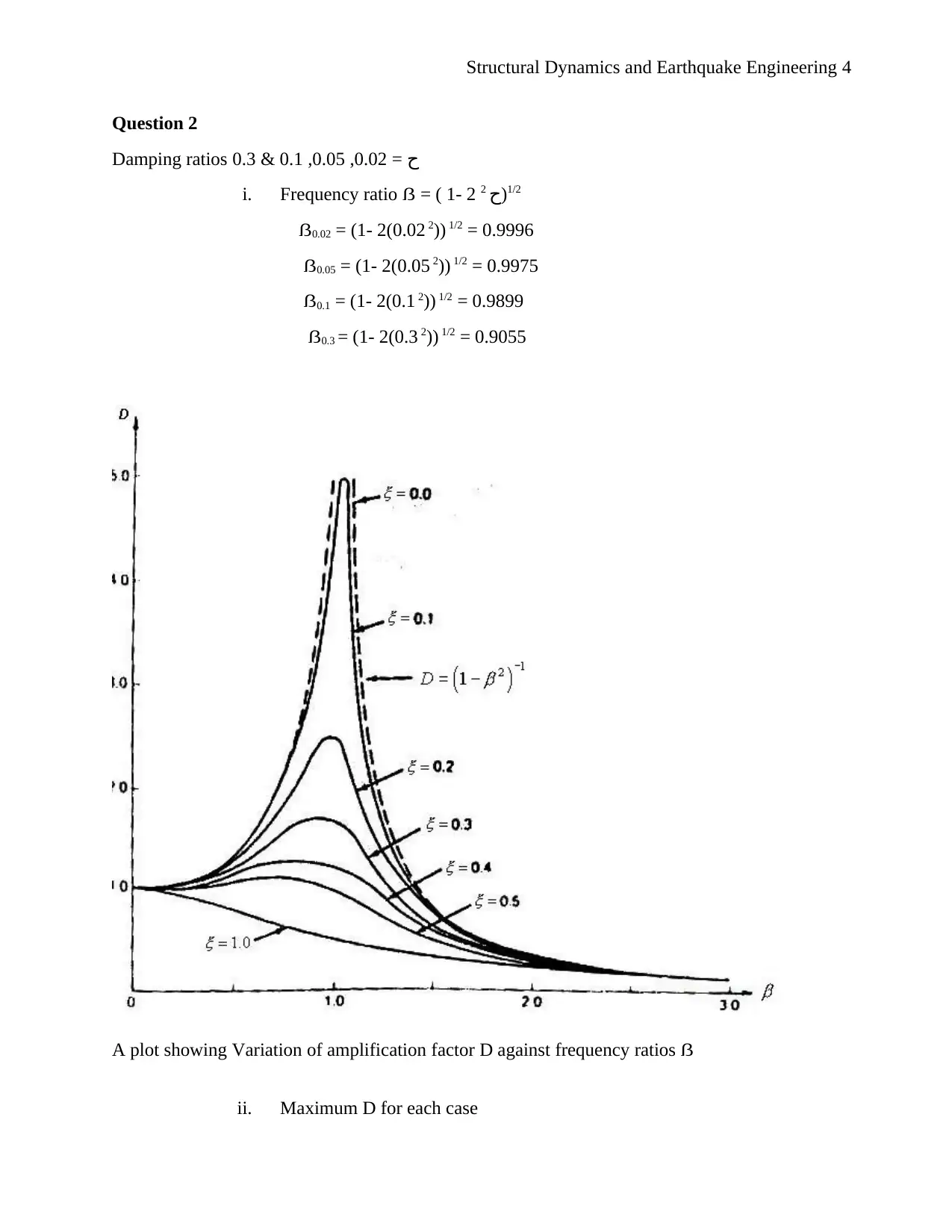
This document presents a complete solution to a Structural Dynamics and Earthquake Engineering assignment from Spring 2018. The assignment covers several key concepts, including calculating circular and cyclic frequencies, determining amplitude and phase angles, and analyzing the effects of damping ratios on structural behavior. It also includes problems involving the computation of critical damping, damped natural frequencies, and the application of the half bandwidth method. Furthermore, the solution explores the relationship between frequency ratios and amplification factors, as well as the calculation of maximum base shear and overturning moments in structural systems. The assignment utilizes formulas and calculations to solve each problem, providing a comprehensive understanding of the principles of structural dynamics and earthquake engineering. The document also includes references to relevant academic resources.

Structural Dynamics and Earthquake Engineering 1
STRUCTURAL DYNAMICS AND EARTHQUAKE ENGINEERING
SPRING 2018 ASSIGNMENT 1
By
(Name)
(Course)
(Professor’s Name)
(Institution)
(State)
(Date)

Structural Dynamics and Earthquake Engineering 2
Question 1
Mass=2535.6t = 25356KN
Stiffness K = 100,000KN/m
a) Circular frequency ω = (Stiffness K/mass m)1/2
ω = (100,000/25,356)1/2
ω =1.9859rad/s
Cyclic frequency f= ω/2∏
f= 1.9859/2∏
f=0.316Hz
b) Velocity ῡo=10m/s, Displacement Uo =1.0m, Circular frequency ω = 1.9859rad/s
Amplitude p = (Uo2 + (ῡo/ ω) 2)1/2
p = (1.02 + (5.0355) 2)1/2 = 5.134m
Phase angle Ө is given by tan Ө= -ῡo/ Uo ω= -10/1.9859
Ө=tan-1-(5.0355) = -78.770
A plot of displacement against time t
Where Vo = 1.0m, T= 3sec, Amplitude p = 5m and Phase angle = 78.770

Structural Dynamics and Earthquake Engineering 3
c) Critical damping Cc is given by= 2 x mass x circular frequency= 2mω
Cc = 2 x 25356 x 1.9859
Cc = 100,708.96
d) Damping ratio = ﺡ0.07
Damped circular natural frequency is given by ωd = ω (1- ﺡ2 )1/2
ωd = 1.9859 (1- 0.072)1/2
ωd= 1.9810 rad/s
Amplitude p is given by p = (Uo2 + (ῡo + ﺡ ω Uo/ ωd) 2)1/2
p = (1.02 + (10 + 0 1.9859x1x07. 0/ 1.9810) 2)1/2
P = 5.215m
Phase angle Ө is given by tan Ө= ﺡ ω Uo -ῡo/ Uo ωd
tan Ө= 0.07 x 1.9859 x 1 – 10 / 1 x 1.9810
Ө= - 78.640
e) Damping ratio = ﺡ0.9
Damped circular natural frequency is given by ωd = ω (1- ﺡ2 )1/2
ωd = 1.9859 (1- 0.92)1/2
ωd= 0.8656 rad/s
Damped cyclic frequency is given by fd= ωd/2∏
fd= 0.8656/2∏ = 0.1378Hz
Period = 1/ fd = 1/0.1378 = 7.258 sec

Structural Dynamics and Earthquake Engineering 4
Question 2
Damping ratios = ﺡ0.02,0.05,0.1&0.3
i. Frequency ratio ẞ = ( 1- 2 ﺡ2 )1/2
ẞ0.02 = (1- 2(0.02 2)) 1/2 = 0.9996
ẞ0.05 = (1- 2(0.05 2)) 1/2 = 0.9975
ẞ0.1 = (1- 2(0.1 2)) 1/2 = 0.9899
ẞ0.3 = (1- 2(0.3 2)) 1/2 = 0.9055
A plot showing Variation of amplification factor D against frequency ratios ẞ
ii. Maximum D for each case

Structural Dynamics and Earthquake Engineering 5
It is given by, D= ((1- ẞ2) + (2ﺡ ẞ) 2)-1/2
D0.02= ((1- 0.99962) + (2x0.02 x 0.9996) 2)-1/2 = 25.005
D0.05= ((1- 0.99752) + (2 x0.05 x 0.9975) 2)-1/2 = 10.01
D0.1= ((1- 0.98992) + (2x0.1 x 0.9899) 2)-1/2 = 5.025
D0.3= ((1- 0.90552) + (2x0.3 x 0.9055) 2)-1/2 = 1.747
iii. Damping ratio = 0.02
Applied load frequency=11Hz
Natural frequency= 12Hz
Frequency ratio= applied load frequency/natural frequency =
11/12=0.9167
D= ((1- ẞ2) + (2ﺡ ẞ) 2)-1/2
D= ((1- 0.91672) + (2x0.02 x 0.9167) 2)-1/2
D= 10.987
Question 3
Mass=20KN
Frequency f = 100 Hz
Damping ratio = ﺡ0.2
Cyclic frequency f= ω/2∏
Rearranging the equation we get,
Circular frequency ω= f/2∏
ω= 100/2∏ = 15.91rad/s

Structural Dynamics and Earthquake Engineering 6
But ω= (Stiffness K/mass m)1/2
Rearranging the equation,
Stiffness K = ω2m
Therefore,
Stiffness K = 15.91220 = 5066.06 KN/m
Question 4
An equation on the computation of a damping ratio by half bandwidth method.
The parameters used are;
Amplification factor D
Damping ratio of critical damping ﺡ
The half bandwidth method is given by D= 1/2 ﺡ,
Rearranging the equation we get,
D/2= ﺡ
i.e Damping ratio of critical damping is half Amplification factor.
Question 5
Mass = 600t
K = 7000KN/m
Height = 15m
Max displacement = Stiffnes/maximum applied force = 250/7000= 0.0357m
Max base shear = (sum of square Force applied) 1/2 = (1002 + 1002 + 2502 + 2502)1/2=
380.79KN
Max Overturning moment = Max shear x height = 380.79 x 15 = 5711.83KNm

Structural Dynamics and Earthquake Engineering 7
Reference
Kausel, E. (2017). Advanced structural dynamics. Available from:
http://dx.doi.org/10.1017/9781316761403. Accessed on; 28th August 2018.
PapadrakakēS, M. (2009). Computational structural dynamics and earthquake
engineering. Boca Raton, CRC Press/Taylor & Francis.