Summary of Week 1 Coulombs Law Experiment

This lab report aims at testing the hypothesis outlining the electrostatic forces as well as acts in line with the inverse square law. The analysis is taken in comparison to the Coulomb law as the theorized item.

Summary of the Week 1 “Coulombs Law” Experiment
This lab report aims at testing the hypothesis outlining the electrostatic forces as well as acts in line
with the inverse square law. The analysis is taken in comparison to the Coulomb law as the
theorized item. Furthermore, it aims at evaluating and determining the experimental Coulomb
constant value. The experimental analysis comprises of applying two charging insulated spheres.
The charging often conducted via the application of excess charge demarcated with the high
voltage. Preferably, it is important to momentarily move the spheres closer to each other and take
the readings for the overall applied forces between the used spheres. The measuring of the overall
applied force per the sphere involve fixing of the one sphere at the moving slide as well as
mounting of other sphere on a makeable horizontal pendulum. The two norms must be supported
by applying the string with demarcated tension. Also torsion by twisting the parametric dial can be
applied in the process. Measuring of the required torsion for maintaining the repelling spheres often
gathered by increasing the torsion realignment in the overall second phase. The essence of the
process is to enable the two repelling spheres to be hold at the static state irrespective of the
difference in the distances1. Thus, the torsion measured in the process thereby related to the
makeable applied force.
Equations referenced:
Coulomb’s Law equation mainly given as
F=k Q1 Q2
r 2 ……………………………..eqn 1
Where
F is force
k is theCoulomb Constant ( 8.99 x 10 9)
Q isthe charge of each charge source
r is thedistance between thetwo charges
For Torsion−Forcerelation :
F=kt θ…………………………………eqn 2
Where
F is force
kt is a constant of proportionality
θ is theangle turned by the dial
Summary of Results
The analysis is appraised by plotting the overall inverse distance square existing between the
spheres against the angle turned in line with the dial in ensuring that the sphere is maintained at the
checked position. This analysis aims at verifying the relationship between the force and the
parametric distance of which the Coulombs law forecast. If the obtained gradient is linear and it
tends to intersect at the makeable original point, then presumably the gathered resulted results often
appraised as correct as per the relationship.
1 Fabiola, Juarez, Dominguez-Flores Aleksej, Goduljan Leila, Mohammadzadeh Paola, Quaino Elizabeth, and Santos
Wolfgang. "Defying Coulomb's law: A lattice-induced attraction between lithium ions." Carbon (2018).

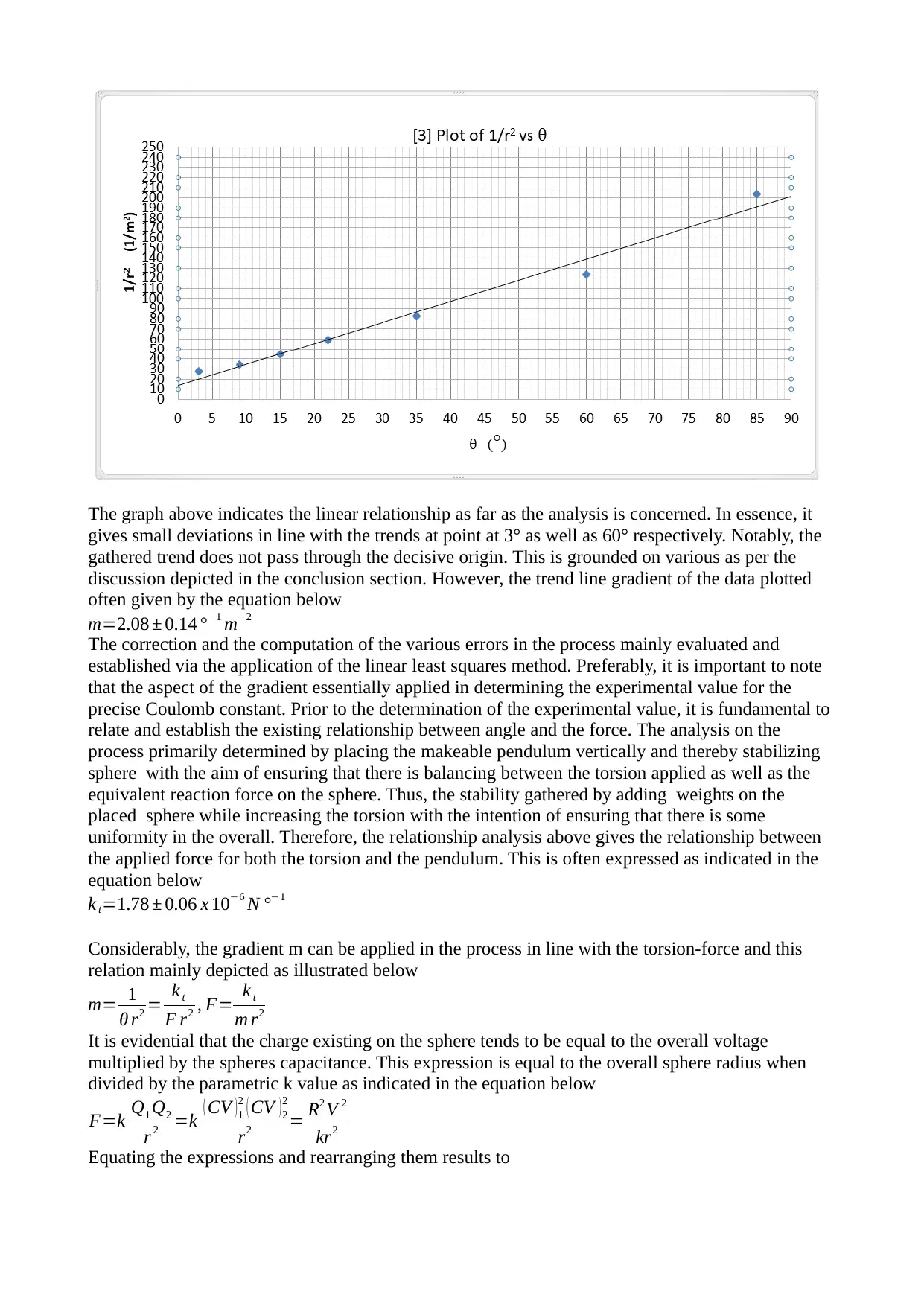
The graph above indicates the linear relationship as far as the analysis is concerned. In essence, it
gives small deviations in line with the trends at point at 3° as well as 60° respectively. Notably, the
gathered trend does not pass through the decisive origin. This is grounded on various as per the
discussion depicted in the conclusion section. However, the trend line gradient of the data plotted
often given by the equation below
m=2.08 ± 0.14 °−1 m−2
The correction and the computation of the various errors in the process mainly evaluated and
established via the application of the linear least squares method. Preferably, it is important to note
that the aspect of the gradient essentially applied in determining the experimental value for the
precise Coulomb constant. Prior to the determination of the experimental value, it is fundamental to
relate and establish the existing relationship between angle and the force. The analysis on the
process primarily determined by placing the makeable pendulum vertically and thereby stabilizing
sphere with the aim of ensuring that there is balancing between the torsion applied as well as the
equivalent reaction force on the sphere. Thus, the stability gathered by adding weights on the
placed sphere while increasing the torsion with the intention of ensuring that there is some
uniformity in the overall. Therefore, the relationship analysis above gives the relationship between
the applied force for both the torsion and the pendulum. This is often expressed as indicated in the
equation below
k t=1.78 ± 0.06 x 10−6 N °−1
Considerably, the gradient m can be applied in the process in line with the torsion-force and this
relation mainly depicted as illustrated below
m= 1
θ r2 = k t
F r2 , F= k t
m r2
It is evidential that the charge existing on the sphere tends to be equal to the overall voltage
multiplied by the spheres capacitance. This expression is equal to the overall sphere radius when
divided by the parametric k value as indicated in the equation below
F=k Q1 Q2
r 2 =k ( CV ) 1
2 ( CV ) 2
2
r2 = R2 V 2
kr2
Equating the expressions and rearranging them results to

k = R2 V 2 m
kt
From the analysis, the measured values for both the sphere radius and the voltage recorded as 1.75
± 0.1 cm as well as 6000 ± 50 volts respectively2. Conversely, it is important to note that the
measurement errors results from the minimum intervals applied on both makeable instrument
utilized in the process. Moreover, the values are input as per the analysis and the value of k obtained
in the end depicted as
k = 12.9 ± 2.5 x109 N m2 C-2
The errors obtained in the process resulted from the propagations of the parametric uncertainties
method.
Conclusions
The trend line obtained indicates conformity in relation to the liner aspect. The aspect therefore
verifies the Coulomb’s law application in line with the inverse square function. Preferably, the trend
line intersects far away from origin even when the theoretical errors are incorporated in the process.
Conversely, resistive force is one factor which accounts for the unaccounted error and this force
results from the weaker two sphere repulsion. If there is larger distance, then there will a total
reduction in the apparent repulsion and this aims at ensuring that the angle measured is often
smaller in the long run. Also, inaccurate gauging of the true deflection measurement is also another
cause of the error recorded in the process. Essentially, there major challenge associated with the
process is the loosing of the charges to the immediate surroundings from the sphere surface. The
losses encountered from the sphere ranges from few seconds to half minute depending on
improvements which one puts in the process. Time limit is also essential element which was
considered in this experiment. Only, estimates were taken in line with the time series applied in the
process and thus, at some instances pendulum was not allowed to settle. The end results of this are
that the closer data points often affected and thereby altering entire system. The internationally
accepted value for the Coulomb constant mainly estimated at 8.99x109 N m2 C-2. The data gathered
from the analysis mainly estimated to conform to the accepted terms and the estimated percentage
value is 40%.
2 Juarez, Fernanda, Fabiola Dominguez-Flores, Aleksej Goduljan, Leila Mohammadzadeh, Paola Quaino, Elizabeth
Santos, and Wolfgang Schmickler. "Defying Coulomb's law: A lattice-induced attraction between lithium
ions." Carbon 139 (2018): 808-812.

References
Fabiola, Juarez, Dominguez-Flores Aleksej, Goduljan Leila, Mohammadzadeh Paola, Quaino
Elizabeth, and Santos Wolfgang. "Defying Coulomb's law: A lattice-induced attraction between
lithium ions." Carbon (2018).
Juarez, Fernanda, Fabiola Dominguez-Flores, Aleksej Goduljan, Leila Mohammadzadeh, Paola
Quaino, Elizabeth Santos, and Wolfgang Schmickler. "Defying Coulomb's law: A lattice-induced
attraction between lithium ions." Carbon 139 (2018): 808-812.