Open University M248 TMA 05: Statistical Analysis and Interpretation
VerifiedAdded on 2023/04/19
|5
|839
|152
Homework Assignment
AI Summary
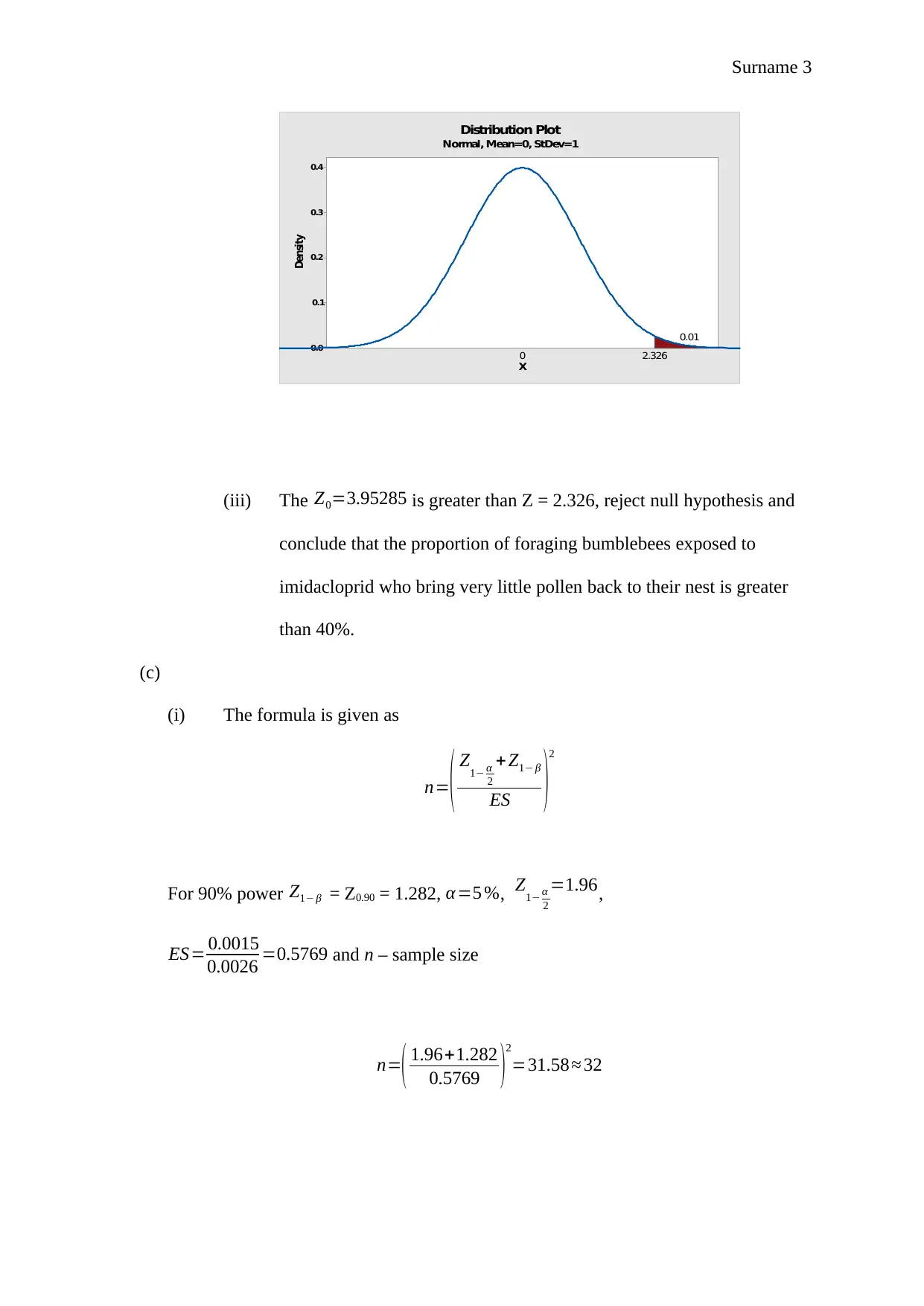
This document presents a comprehensive solution to the M248 TMA 05 assignment, focusing on statistical analysis techniques. The solution addresses two main questions. Question 1 explores hypothesis testing using z-tests, calculating p-values, and interpreting results in the context of fiber strength and bumblebee foraging. It also includes a sample size calculation. Question 2 delves into non-parametric tests, specifically the Mann-Whitney test for comparing triglyceride levels and the Chi-square goodness-of-fit test for analyzing Victorian deaths. The solution provides detailed steps, interpretations of statistical outputs, and conclusions based on significance levels, providing a thorough understanding of the statistical methods applied and the interpretation of the results. The assignment covers hypothesis testing, statistical tests, p-values, and interpretation of the results.
1 out of 5









![[object Object]](/_next/static/media/star-bottom.7253800d.svg)