SYSTEM IDENTIFICATION AND MODEL PREDICTIVE CONTROL.
VerifiedAdded on 2022/11/14
|6
|1037
|55
AI Summary
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Running head: SYSTEM IDENTIFICATION AND MODEL PREDICTIVE CONTROL
SYSTEM IDENTIFICATION AND MODEL PREDICTIVE CONTROL
Name of the Student
Name of the University
Author Note
SYSTEM IDENTIFICATION AND MODEL PREDICTIVE CONTROL
Name of the Student
Name of the University
Author Note
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

SYSTEM IDENTIFICATION AND MODEL PREDICTIVE CONTROL
Introduction:
In this assignment the two methods of fitting pulse transfer function model namely the
Young’s Information Criterion (YIC) and the least square method is discussed along with the
their corresponding equations and assumptions. Furthermore, the two methods are employed
to fit the pulse transfer function model to a sample exponential rig data sample at every 0.1
second given in the ica_2019.mat file with the help of MATLAB. In general structure of the
pulse transfer function model is presented below. The YIC method contains linear regression
or least square fit model as given in the yic.m matlab code.
1) The least square and the YIC method can be used to generate the parameters of pulse
transfer function model. The least square model is also known as the regression model to
generate the pulse transfer function model of a time series data with suitable parameters. The
least square input-output relationship is given by,
yt =b 0+b 1∗x 1 t+ b 2∗x 2 t+ …+bk∗xkt+ut
Here, y_t = output variable of tth observation.
xkt = the kth input variable at the tth observation.
b = regression coefficients
ut = the residual at tth observation.
k = the number of input variables
n = number of observations
The pulse transfer function relates the z transform of the output in different instants of the
sampled input signal (chai et al. 2017).
The pulse transfer function of a SISO system is given by,
yt= ( A ( B )
C ( B ) )∗xt−b +ut
Here, A(B) = A0 – A1*B -….- AB*B
A0,… AB are model parameters.
YIC is a new data based modelling system of pulse transfer function model which is defined
as
YIC = log ¿ + log ( 1
nθ )* ∑
i=1
nθ πii
pi
Here, πii is the ith and ith element of the covariance matrix Pp correlated with p.
The lower the value of YIC lower the accuracy of the fitted model (Youngs et al. 2019).
2.
In this section the pulse transfer function model is selected based on the YIC score of three
models. Also, the fitted model with actual time series data is superimposed in graph to
visualize the accuracy of fits. Before running the matlab function the 1000 pairs of measured
input output data is loaded in matlab.
Introduction:
In this assignment the two methods of fitting pulse transfer function model namely the
Young’s Information Criterion (YIC) and the least square method is discussed along with the
their corresponding equations and assumptions. Furthermore, the two methods are employed
to fit the pulse transfer function model to a sample exponential rig data sample at every 0.1
second given in the ica_2019.mat file with the help of MATLAB. In general structure of the
pulse transfer function model is presented below. The YIC method contains linear regression
or least square fit model as given in the yic.m matlab code.
1) The least square and the YIC method can be used to generate the parameters of pulse
transfer function model. The least square model is also known as the regression model to
generate the pulse transfer function model of a time series data with suitable parameters. The
least square input-output relationship is given by,
yt =b 0+b 1∗x 1 t+ b 2∗x 2 t+ …+bk∗xkt+ut
Here, y_t = output variable of tth observation.
xkt = the kth input variable at the tth observation.
b = regression coefficients
ut = the residual at tth observation.
k = the number of input variables
n = number of observations
The pulse transfer function relates the z transform of the output in different instants of the
sampled input signal (chai et al. 2017).
The pulse transfer function of a SISO system is given by,
yt= ( A ( B )
C ( B ) )∗xt−b +ut
Here, A(B) = A0 – A1*B -….- AB*B
A0,… AB are model parameters.
YIC is a new data based modelling system of pulse transfer function model which is defined
as
YIC = log ¿ + log ( 1
nθ )* ∑
i=1
nθ πii
pi
Here, πii is the ith and ith element of the covariance matrix Pp correlated with p.
The lower the value of YIC lower the accuracy of the fitted model (Youngs et al. 2019).
2.
In this section the pulse transfer function model is selected based on the YIC score of three
models. Also, the fitted model with actual time series data is superimposed in graph to
visualize the accuracy of fits. Before running the matlab function the 1000 pairs of measured
input output data is loaded in matlab.
SYSTEM IDENTIFICATION AND MODEL PREDICTIVE CONTROL
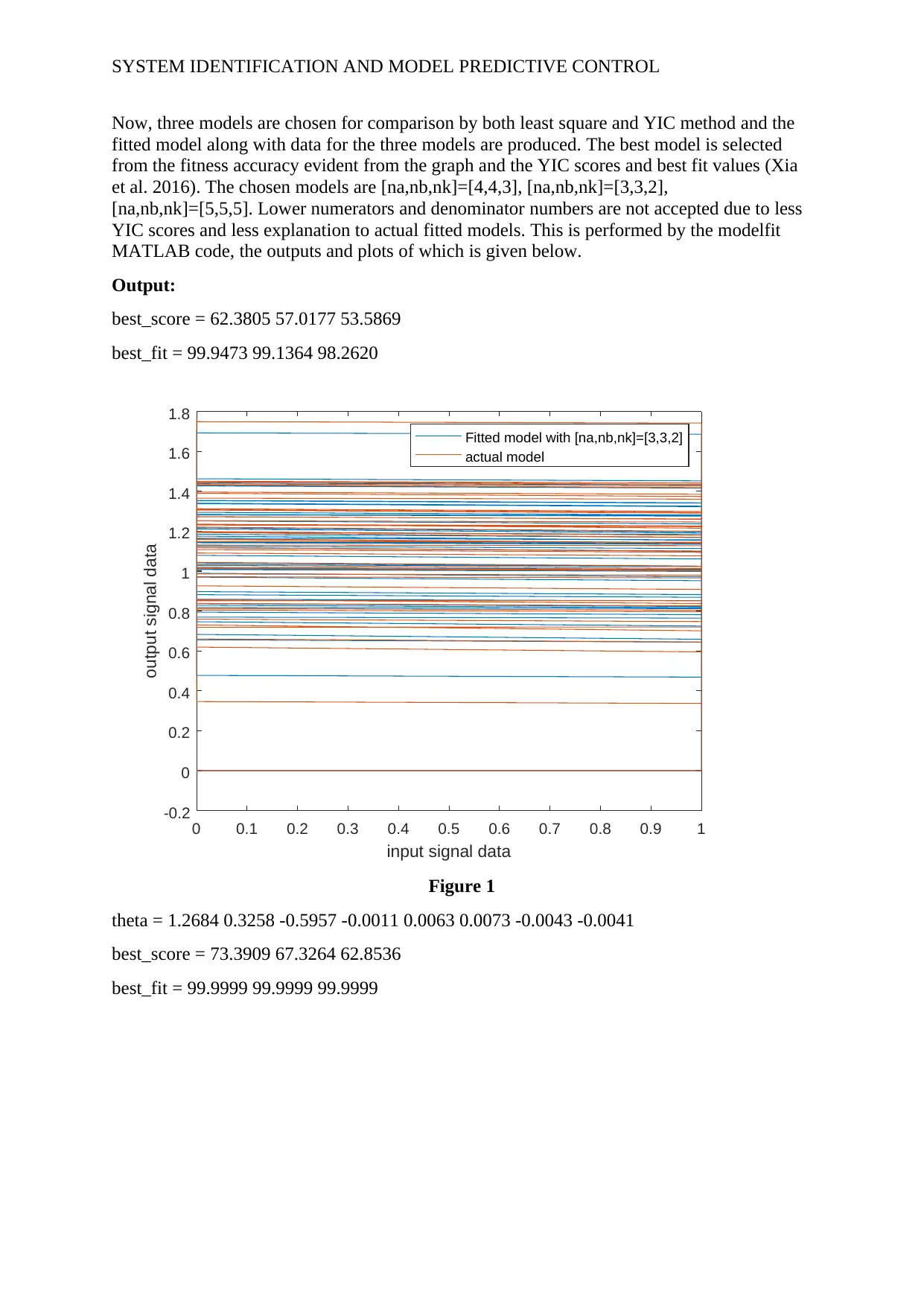
Now, three models are chosen for comparison by both least square and YIC method and the
fitted model along with data for the three models are produced. The best model is selected
from the fitness accuracy evident from the graph and the YIC scores and best fit values (Xia
et al. 2016). The chosen models are [na,nb,nk]=[4,4,3], [na,nb,nk]=[3,3,2],
[na,nb,nk]=[5,5,5]. Lower numerators and denominator numbers are not accepted due to less
YIC scores and less explanation to actual fitted models. This is performed by the modelfit
MATLAB code, the outputs and plots of which is given below.
Output:
best_score = 62.3805 57.0177 53.5869
best_fit = 99.9473 99.1364 98.2620
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
input signal data
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
output signal data
Fitted model with [na,nb,nk]=[3,3,2]
actual model
Figure 1
theta = 1.2684 0.3258 -0.5957 -0.0011 0.0063 0.0073 -0.0043 -0.0041
best_score = 73.3909 67.3264 62.8536
best_fit = 99.9999 99.9999 99.9999
Now, three models are chosen for comparison by both least square and YIC method and the
fitted model along with data for the three models are produced. The best model is selected
from the fitness accuracy evident from the graph and the YIC scores and best fit values (Xia
et al. 2016). The chosen models are [na,nb,nk]=[4,4,3], [na,nb,nk]=[3,3,2],
[na,nb,nk]=[5,5,5]. Lower numerators and denominator numbers are not accepted due to less
YIC scores and less explanation to actual fitted models. This is performed by the modelfit
MATLAB code, the outputs and plots of which is given below.
Output:
best_score = 62.3805 57.0177 53.5869
best_fit = 99.9473 99.1364 98.2620
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
input signal data
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
output signal data
Fitted model with [na,nb,nk]=[3,3,2]
actual model
Figure 1
theta = 1.2684 0.3258 -0.5957 -0.0011 0.0063 0.0073 -0.0043 -0.0041
best_score = 73.3909 67.3264 62.8536
best_fit = 99.9999 99.9999 99.9999
SYSTEM IDENTIFICATION AND MODEL PREDICTIVE CONTROL
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
input signal data
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
output signal data
Fitted model with [na,nb,nk]=[4,4,3]
actual model
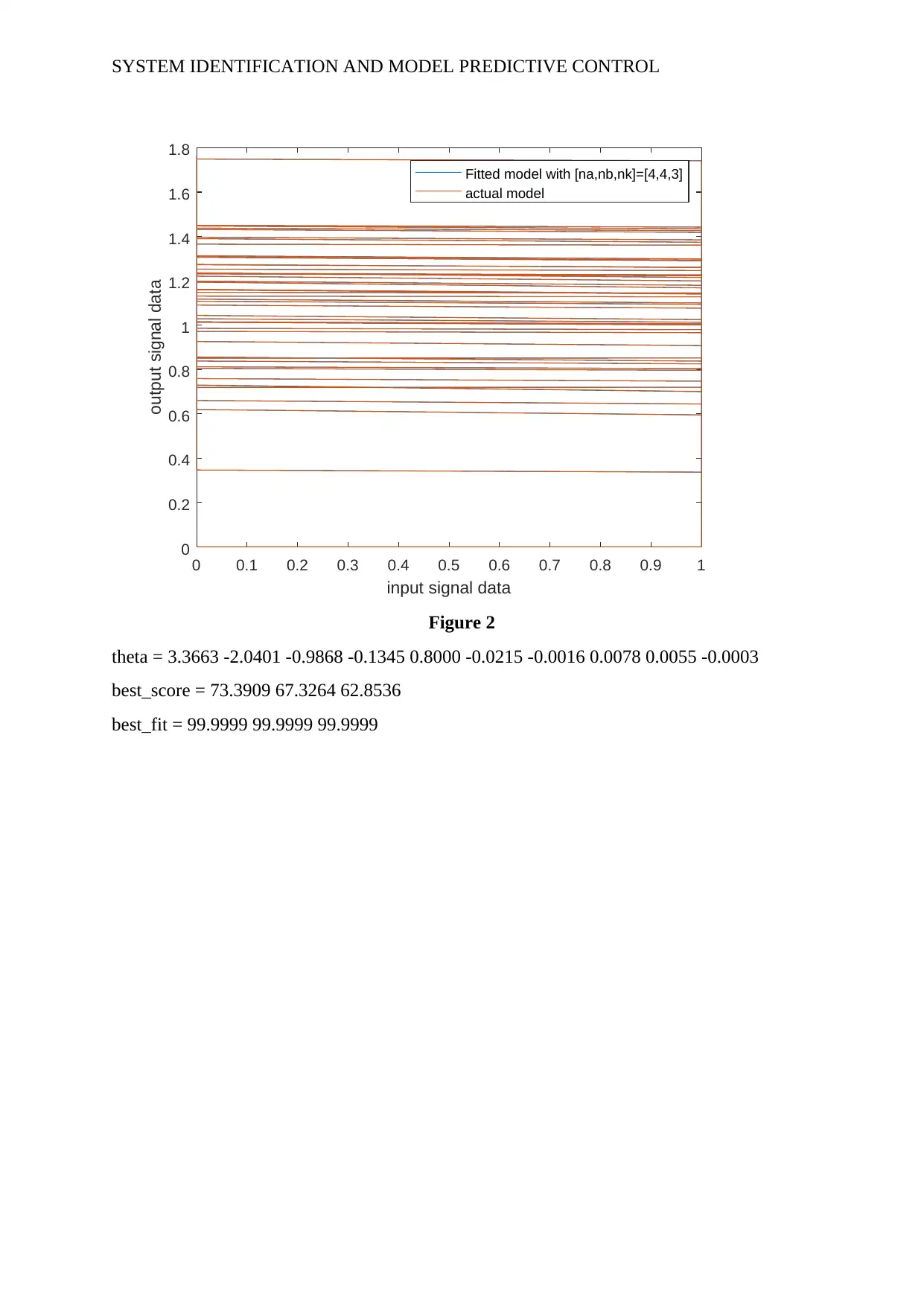
Figure 2
theta = 3.3663 -2.0401 -0.9868 -0.1345 0.8000 -0.0215 -0.0016 0.0078 0.0055 -0.0003
best_score = 73.3909 67.3264 62.8536
best_fit = 99.9999 99.9999 99.9999
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
input signal data
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
output signal data
Fitted model with [na,nb,nk]=[4,4,3]
actual model
Figure 2
theta = 3.3663 -2.0401 -0.9868 -0.1345 0.8000 -0.0215 -0.0016 0.0078 0.0055 -0.0003
best_score = 73.3909 67.3264 62.8536
best_fit = 99.9999 99.9999 99.9999
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
SYSTEM IDENTIFICATION AND MODEL PREDICTIVE CONTROL
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
input signal data
-7
-6
-5
-4
-3
-2
-1
0
output signal data
10307
Fitted model with [na,nb,nk]=[5,5,4]
actual model
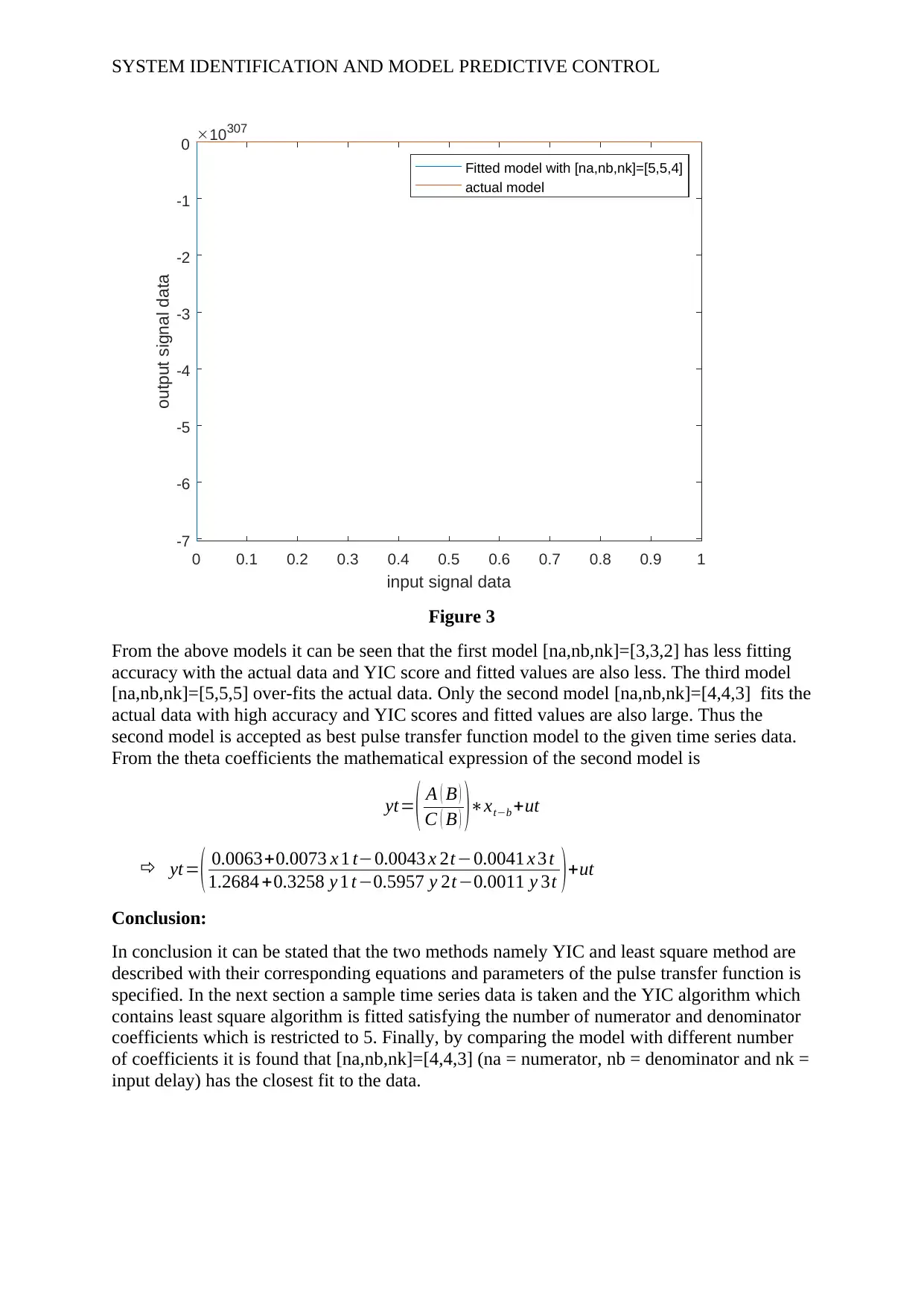
Figure 3
From the above models it can be seen that the first model [na,nb,nk]=[3,3,2] has less fitting
accuracy with the actual data and YIC score and fitted values are also less. The third model
[na,nb,nk]=[5,5,5] over-fits the actual data. Only the second model [na,nb,nk]=[4,4,3] fits the
actual data with high accuracy and YIC scores and fitted values are also large. Thus the
second model is accepted as best pulse transfer function model to the given time series data.
From the theta coefficients the mathematical expression of the second model is
yt= ( A ( B )
C ( B ) )∗xt−b +ut
yt= ( 0.0063+0.0073 x 1 t−0.0043 x 2t−0.0041 x 3 t
1.2684 +0.3258 y 1 t−0.5957 y 2t−0.0011 y 3t )+ut
Conclusion:
In conclusion it can be stated that the two methods namely YIC and least square method are
described with their corresponding equations and parameters of the pulse transfer function is
specified. In the next section a sample time series data is taken and the YIC algorithm which
contains least square algorithm is fitted satisfying the number of numerator and denominator
coefficients which is restricted to 5. Finally, by comparing the model with different number
of coefficients it is found that [na,nb,nk]=[4,4,3] (na = numerator, nb = denominator and nk =
input delay) has the closest fit to the data.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
input signal data
-7
-6
-5
-4
-3
-2
-1
0
output signal data
10307
Fitted model with [na,nb,nk]=[5,5,4]
actual model
Figure 3
From the above models it can be seen that the first model [na,nb,nk]=[3,3,2] has less fitting
accuracy with the actual data and YIC score and fitted values are also less. The third model
[na,nb,nk]=[5,5,5] over-fits the actual data. Only the second model [na,nb,nk]=[4,4,3] fits the
actual data with high accuracy and YIC scores and fitted values are also large. Thus the
second model is accepted as best pulse transfer function model to the given time series data.
From the theta coefficients the mathematical expression of the second model is
yt= ( A ( B )
C ( B ) )∗xt−b +ut
yt= ( 0.0063+0.0073 x 1 t−0.0043 x 2t−0.0041 x 3 t
1.2684 +0.3258 y 1 t−0.5957 y 2t−0.0011 y 3t )+ut
Conclusion:
In conclusion it can be stated that the two methods namely YIC and least square method are
described with their corresponding equations and parameters of the pulse transfer function is
specified. In the next section a sample time series data is taken and the YIC algorithm which
contains least square algorithm is fitted satisfying the number of numerator and denominator
coefficients which is restricted to 5. Finally, by comparing the model with different number
of coefficients it is found that [na,nb,nk]=[4,4,3] (na = numerator, nb = denominator and nk =
input delay) has the closest fit to the data.

SYSTEM IDENTIFICATION AND MODEL PREDICTIVE CONTROL
References:
Chai, R., Xu, L.S., Yao, Y., Hao, L.L. and Qi, L., 2017. Comparison of Regression Analysis
and Transfer Function in Estimating the Parameters of Central Pulse Waves from Brachial
Pulse Wave. Studies in health technology and informatics, 245, pp.573-577.
Xia, B., Zhao, X., de Callafon, R., Garnier, H., Nguyen, T. and Mi, C., 2016. Accurate
Lithium-ion battery parameter estimation with continuous-time system identification
methods. Applied energy, 179, pp.426-436.
Youngs, J., Marshall, B., Farragher, M., Whitney, L., Glass, S., Pope, C., Planche, T., Riley,
P. and Carrington, D., 2019. Implementation of influenza point-of-care testing and patient
cohorting during a high-incidence season: a retrospective analysis of impact on infection
prevention and control and clinical outcomes. Journal of Hospital Infection, 101(3), pp.276-
284.
References:
Chai, R., Xu, L.S., Yao, Y., Hao, L.L. and Qi, L., 2017. Comparison of Regression Analysis
and Transfer Function in Estimating the Parameters of Central Pulse Waves from Brachial
Pulse Wave. Studies in health technology and informatics, 245, pp.573-577.
Xia, B., Zhao, X., de Callafon, R., Garnier, H., Nguyen, T. and Mi, C., 2016. Accurate
Lithium-ion battery parameter estimation with continuous-time system identification
methods. Applied energy, 179, pp.426-436.
Youngs, J., Marshall, B., Farragher, M., Whitney, L., Glass, S., Pope, C., Planche, T., Riley,
P. and Carrington, D., 2019. Implementation of influenza point-of-care testing and patient
cohorting during a high-incidence season: a retrospective analysis of impact on infection
prevention and control and clinical outcomes. Journal of Hospital Infection, 101(3), pp.276-
284.
1 out of 6
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.




