Finance Assignment: Risk, Return, and Investment Analysis
VerifiedAdded on 2019/10/01
|9
|1804
|205
Homework Assignment
AI Summary
This finance assignment presents solutions to various financial calculations and analyses. It includes present value calculations, revenue growth predictions, effective annual rate computations for different loan scenarios, and EMI calculations for property financing. The assignment also delves into yield to maturity calculations for bonds and applies the Capital Asset Pricing Model (CAPM) to estimate expected returns for securities, considering beta, risk-free rates, and market risk premiums. The analysis extends to a hypothetical company with a negative beta, comparing portfolio returns and discussing the relationship between risk and return in financial investments. The document references key financial concepts and models, providing a comprehensive overview of financial analysis.

Table of Contents
Solution –A.....................................................................................................................2
Solution –B.....................................................................................................................2
Solution –C.....................................................................................................................2
Solution –D.....................................................................................................................3
Solution – E....................................................................................................................4
Solution –F.....................................................................................................................4
Risk and Return Estimation............................................................................................5
Risk and Return analyses................................................................................................6
References......................................................................................................................9
1 | P a g e
Solution –A.....................................................................................................................2
Solution –B.....................................................................................................................2
Solution –C.....................................................................................................................2
Solution –D.....................................................................................................................3
Solution – E....................................................................................................................4
Solution –F.....................................................................................................................4
Risk and Return Estimation............................................................................................5
Risk and Return analyses................................................................................................6
References......................................................................................................................9
1 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Solution –A
Total amount paid by the consumers over a period of 4 year are $ 1396.80 ( $ 29.1 X
48 moths) and bank discount that amount at the rate of 7 percentage a year or 0.58
percentage per month, now the Present value of future inflow of $ 1396.80 is $
1065.61.
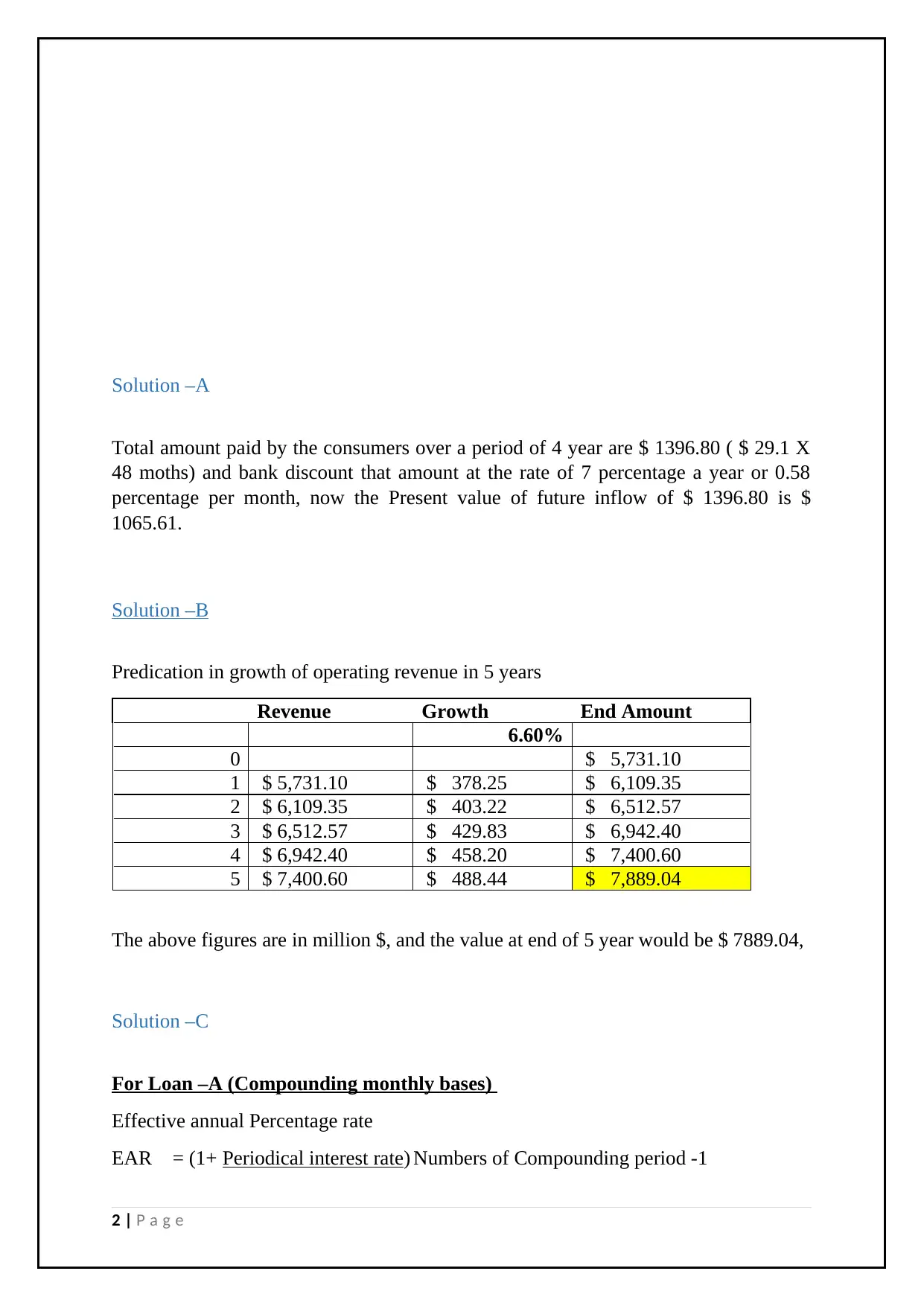
Solution –B
Predication in growth of operating revenue in 5 years
Revenue Growth End Amount
6.60%
0 $ 5,731.10
1 $ 5,731.10 $ 378.25 $ 6,109.35
2 $ 6,109.35 $ 403.22 $ 6,512.57
3 $ 6,512.57 $ 429.83 $ 6,942.40
4 $ 6,942.40 $ 458.20 $ 7,400.60
5 $ 7,400.60 $ 488.44 $ 7,889.04
The above figures are in million $, and the value at end of 5 year would be $ 7889.04,
Solution –C
For Loan –A (Compounding monthly bases)
Effective annual Percentage rate
EAR = (1+ Periodical interest rate) Numbers of Compounding period -1
2 | P a g e
Total amount paid by the consumers over a period of 4 year are $ 1396.80 ( $ 29.1 X
48 moths) and bank discount that amount at the rate of 7 percentage a year or 0.58
percentage per month, now the Present value of future inflow of $ 1396.80 is $
1065.61.
Solution –B
Predication in growth of operating revenue in 5 years
Revenue Growth End Amount
6.60%
0 $ 5,731.10
1 $ 5,731.10 $ 378.25 $ 6,109.35
2 $ 6,109.35 $ 403.22 $ 6,512.57
3 $ 6,512.57 $ 429.83 $ 6,942.40
4 $ 6,942.40 $ 458.20 $ 7,400.60
5 $ 7,400.60 $ 488.44 $ 7,889.04
The above figures are in million $, and the value at end of 5 year would be $ 7889.04,
Solution –C
For Loan –A (Compounding monthly bases)
Effective annual Percentage rate
EAR = (1+ Periodical interest rate) Numbers of Compounding period -1
2 | P a g e

Compounding numbers
= (1 + 0.493/ 12) 12 - 1
= 5.043 %
Form Loan – B (Compounding semi-annual bases)
EAR = (1+ Periodical interest rate) Numbers of Compounding period -1
Compounding numbers
= (1 + 0.05/ 2) 2 -1
= 5.0625 %
For Loan – C (Compounding Daily based) (here days equal to 365 days)
EAR = (1+ Periodical interest rate) Numbers of Compounding period -1
Compounding numbers
= (1+ 0.0491 / 365) 365 -1
= 5. 032 %
Solution –D
Cost of Property $ 574,000 and whole the assets is finance through bank borrowing,
and the bank agreed to finance the assets at the APR Rate of 3.80 %, now the interest
are compounded Quarterly and the payment are made 10 year on monthly bases, in
such case we have to compute the quarterly payment on for monthly instalments.
Total borrowed amount are paid throughout the 10 years on monthly bases at the rate
of 3.80 %.
Monthly EMI would be $ 5757 and the quarterly payment would be $ 17,271.
3 | P a g e
= (1 + 0.493/ 12) 12 - 1
= 5.043 %
Form Loan – B (Compounding semi-annual bases)
EAR = (1+ Periodical interest rate) Numbers of Compounding period -1
Compounding numbers
= (1 + 0.05/ 2) 2 -1
= 5.0625 %
For Loan – C (Compounding Daily based) (here days equal to 365 days)
EAR = (1+ Periodical interest rate) Numbers of Compounding period -1
Compounding numbers
= (1+ 0.0491 / 365) 365 -1
= 5. 032 %
Solution –D
Cost of Property $ 574,000 and whole the assets is finance through bank borrowing,
and the bank agreed to finance the assets at the APR Rate of 3.80 %, now the interest
are compounded Quarterly and the payment are made 10 year on monthly bases, in
such case we have to compute the quarterly payment on for monthly instalments.
Total borrowed amount are paid throughout the 10 years on monthly bases at the rate
of 3.80 %.
Monthly EMI would be $ 5757 and the quarterly payment would be $ 17,271.
3 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Solution – E
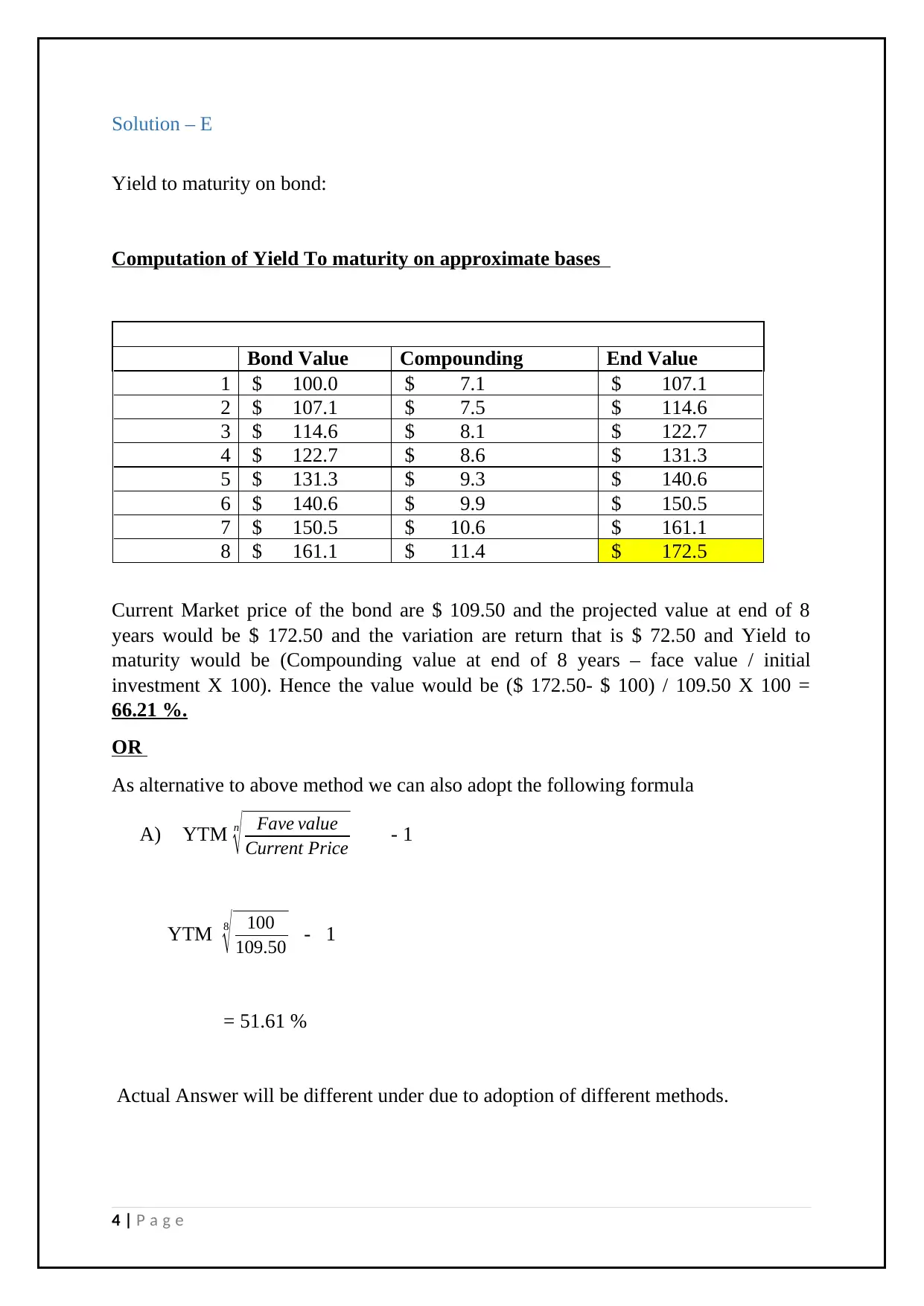
Yield to maturity on bond:
Computation of Yield To maturity on approximate bases
Bond Value Compounding End Value
1 $ 100.0 $ 7.1 $ 107.1
2 $ 107.1 $ 7.5 $ 114.6
3 $ 114.6 $ 8.1 $ 122.7
4 $ 122.7 $ 8.6 $ 131.3
5 $ 131.3 $ 9.3 $ 140.6
6 $ 140.6 $ 9.9 $ 150.5
7 $ 150.5 $ 10.6 $ 161.1
8 $ 161.1 $ 11.4 $ 172.5
Current Market price of the bond are $ 109.50 and the projected value at end of 8
years would be $ 172.50 and the variation are return that is $ 72.50 and Yield to
maturity would be (Compounding value at end of 8 years – face value / initial
investment X 100). Hence the value would be ($ 172.50- $ 100) / 109.50 X 100 =
66.21 %.
OR
As alternative to above method we can also adopt the following formula
A) YTM n
√ Fave value
Current Price - 1
YTM 8
√ 100
109.50 - 1
= 51.61 %
Actual Answer will be different under due to adoption of different methods.
4 | P a g e
Yield to maturity on bond:
Computation of Yield To maturity on approximate bases
Bond Value Compounding End Value
1 $ 100.0 $ 7.1 $ 107.1
2 $ 107.1 $ 7.5 $ 114.6
3 $ 114.6 $ 8.1 $ 122.7
4 $ 122.7 $ 8.6 $ 131.3
5 $ 131.3 $ 9.3 $ 140.6
6 $ 140.6 $ 9.9 $ 150.5
7 $ 150.5 $ 10.6 $ 161.1
8 $ 161.1 $ 11.4 $ 172.5
Current Market price of the bond are $ 109.50 and the projected value at end of 8
years would be $ 172.50 and the variation are return that is $ 72.50 and Yield to
maturity would be (Compounding value at end of 8 years – face value / initial
investment X 100). Hence the value would be ($ 172.50- $ 100) / 109.50 X 100 =
66.21 %.
OR
As alternative to above method we can also adopt the following formula
A) YTM n
√ Fave value
Current Price - 1
YTM 8
√ 100
109.50 - 1
= 51.61 %
Actual Answer will be different under due to adoption of different methods.
4 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Solution –F
Here in current case, company has issue the bond having a face value of $ 1000, with
compounding rate of 7 % Semi-annually, in such as case, we need to apply following
formula.
= Face value X r/ n
Here face value is $ 1000 and annual compounding interest rate are 7 % with semi-
annual bases.
= $ 1000 X 7 % / 2
$ 35
Risk and Return Estimation
I) Computation of Expected return from the securities of Boral Ltd,
CAPM Model
Err = Risk free rate + Beta (Expected return from the market – Risk free rate)
Here Risk free rate = 10-year Australian Government bond, this rate as on 17.04.2019
is 1.98 %.
Market Risk Premium would be 6 %.
Beta of Boral Limited during last 5 years would be 1.14.
Computation of Expected return
ER = 1.98% + 1.14 (6 % - 1.98 %)
= 1.98 % + 4 .58 %
= 6.56 %
5 | P a g e
Here in current case, company has issue the bond having a face value of $ 1000, with
compounding rate of 7 % Semi-annually, in such as case, we need to apply following
formula.
= Face value X r/ n
Here face value is $ 1000 and annual compounding interest rate are 7 % with semi-
annual bases.
= $ 1000 X 7 % / 2
$ 35
Risk and Return Estimation
I) Computation of Expected return from the securities of Boral Ltd,
CAPM Model
Err = Risk free rate + Beta (Expected return from the market – Risk free rate)
Here Risk free rate = 10-year Australian Government bond, this rate as on 17.04.2019
is 1.98 %.
Market Risk Premium would be 6 %.
Beta of Boral Limited during last 5 years would be 1.14.
Computation of Expected return
ER = 1.98% + 1.14 (6 % - 1.98 %)
= 1.98 % + 4 .58 %
= 6.56 %
5 | P a g e
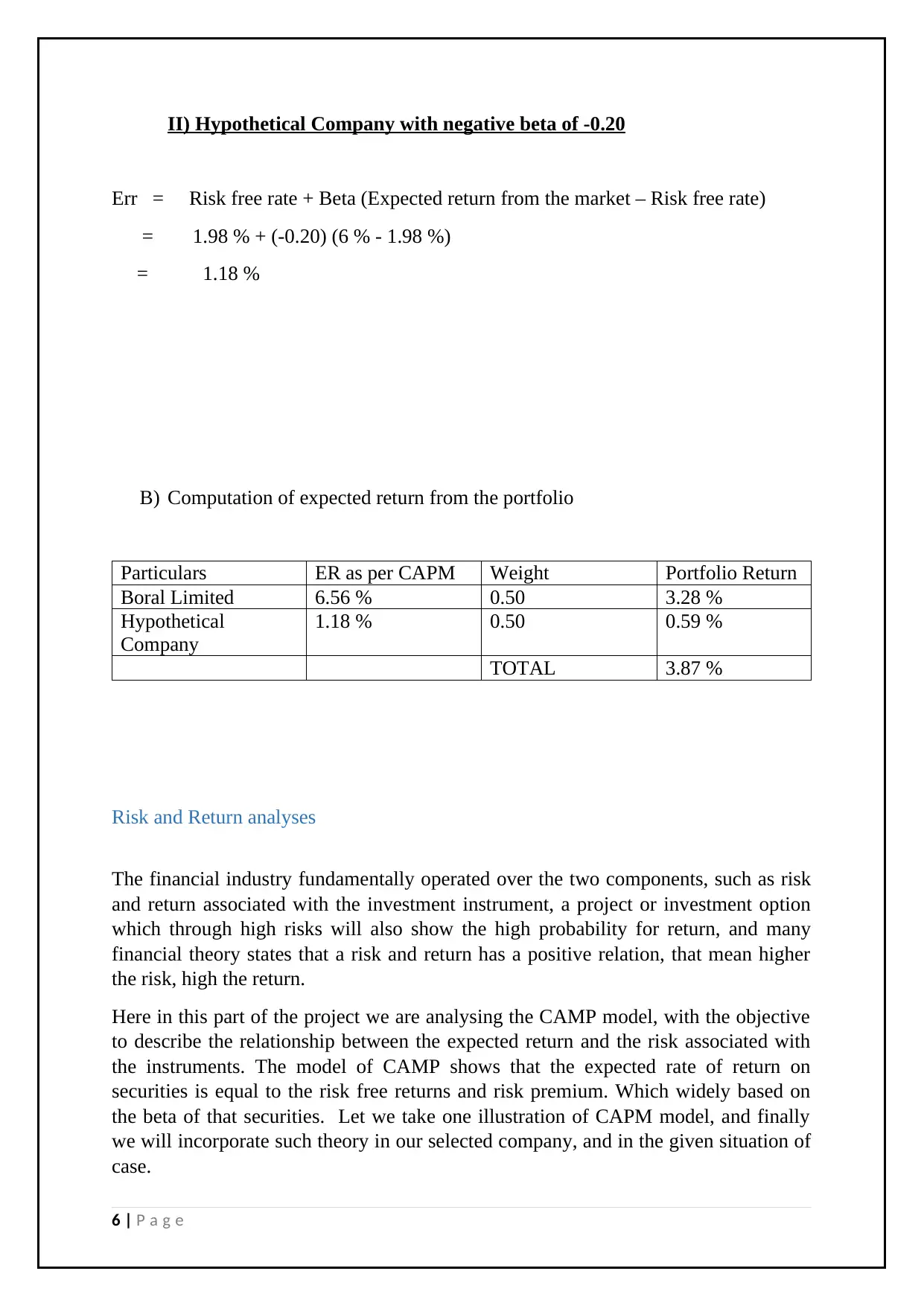
II) Hypothetical Company with negative beta of -0.20
Err = Risk free rate + Beta (Expected return from the market – Risk free rate)
= 1.98 % + (-0.20) (6 % - 1.98 %)
= 1.18 %
B) Computation of expected return from the portfolio
Particulars ER as per CAPM Weight Portfolio Return
Boral Limited 6.56 % 0.50 3.28 %
Hypothetical
Company
1.18 % 0.50 0.59 %
TOTAL 3.87 %
Risk and Return analyses
The financial industry fundamentally operated over the two components, such as risk
and return associated with the investment instrument, a project or investment option
which through high risks will also show the high probability for return, and many
financial theory states that a risk and return has a positive relation, that mean higher
the risk, high the return.
Here in this part of the project we are analysing the CAMP model, with the objective
to describe the relationship between the expected return and the risk associated with
the instruments. The model of CAMP shows that the expected rate of return on
securities is equal to the risk free returns and risk premium. Which widely based on
the beta of that securities. Let we take one illustration of CAPM model, and finally
we will incorporate such theory in our selected company, and in the given situation of
case.
6 | P a g e
Err = Risk free rate + Beta (Expected return from the market – Risk free rate)
= 1.98 % + (-0.20) (6 % - 1.98 %)
= 1.18 %
B) Computation of expected return from the portfolio
Particulars ER as per CAPM Weight Portfolio Return
Boral Limited 6.56 % 0.50 3.28 %
Hypothetical
Company
1.18 % 0.50 0.59 %
TOTAL 3.87 %
Risk and Return analyses
The financial industry fundamentally operated over the two components, such as risk
and return associated with the investment instrument, a project or investment option
which through high risks will also show the high probability for return, and many
financial theory states that a risk and return has a positive relation, that mean higher
the risk, high the return.
Here in this part of the project we are analysing the CAMP model, with the objective
to describe the relationship between the expected return and the risk associated with
the instruments. The model of CAMP shows that the expected rate of return on
securities is equal to the risk free returns and risk premium. Which widely based on
the beta of that securities. Let we take one illustration of CAPM model, and finally
we will incorporate such theory in our selected company, and in the given situation of
case.
6 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
The model of CAMP gives a formula to compute the expected return from the
particular investment option.
Expected return = Risk free rate + (beta X Market risk Premium)
Here,
Expected return does means, how security will be performance over a period of time,
the expected return is a long term assumption about the how the investment will play
out over a useful life.
Risk- Free Rate; here the risk free rate refers to return normally available from the
free risk securities, such as 10 years US governments bond. Such return normally
compensate with the inflection rate prevailing in market. The risk-free rate should
correspond to the country where the investment is being made, and the maturity of the
bond should match the time horizon of the investment. (Fernandez, P. (2014).
Beta: the beta indicate the risk associated with the security that mean variation in the
price due to internal or external controllable or non-controllable factors. The beta also
measure the risk of the stock, it is something like stock sensitive to the market price,
the beta are normally found in the single digits but it is interpreted differently. Let we
assume that a XYZ limited has a beta of 1.5, which indicate that a security of XYZ
limited many be vary between the 150 percentage on an average. But in case the beta
is equal to 1, the expected return on a security is equal to the average market return. A
7 | P a g e
particular investment option.
Expected return = Risk free rate + (beta X Market risk Premium)
Here,
Expected return does means, how security will be performance over a period of time,
the expected return is a long term assumption about the how the investment will play
out over a useful life.
Risk- Free Rate; here the risk free rate refers to return normally available from the
free risk securities, such as 10 years US governments bond. Such return normally
compensate with the inflection rate prevailing in market. The risk-free rate should
correspond to the country where the investment is being made, and the maturity of the
bond should match the time horizon of the investment. (Fernandez, P. (2014).
Beta: the beta indicate the risk associated with the security that mean variation in the
price due to internal or external controllable or non-controllable factors. The beta also
measure the risk of the stock, it is something like stock sensitive to the market price,
the beta are normally found in the single digits but it is interpreted differently. Let we
assume that a XYZ limited has a beta of 1.5, which indicate that a security of XYZ
limited many be vary between the 150 percentage on an average. But in case the beta
is equal to 1, the expected return on a security is equal to the average market return. A
7 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

beta of -1 means security has a perfect negative correlation with the market.
(Fernandez, P. (2014).
Market Risk premium: the fourth important component of the CAPM model is the
market risk premiums, such premium is computed by formulating the expected return
of the market less the risk free rate. Such marker risk premium presents the additional
return over and above the risk free rate. (Corporate Finance Institute. (2019).
Now in current case:
our selected corporate operate with the beta of 1.14 % during the last five financial
year, this similar indicates that a security of Boral Limited may be vary by nearly 114
%, from the prevailing market price and actual return will be vary by 1.14 time . The
expected and risk free rate is 1.98 % this rate is the rate of 10 year Australian Security
risk free bonds. While the market risk premiums is 6 % this risk premium is reduced
by the risk free rate, in order to measure the effective rate. The selected security is
comparatively lower riskers than the hypothecated security which own a negative
beta,
the negative beta or beta less than Zero, indicates that an investment relating to market
are possible but such investments are higher risky in nature, the actual return from the
security is comparatively low due to lack of volatility and risk in the security, such
type of beta are normally found in case of Gold and similar investment option when
the possibility for variation in price are comparatively lower than what we can
normally note under the normal circumstance of securities. (Finance.zacks.com.
(2019).
After analysing the performance both the securities which we have selected in the
current case, we can concludes that security of Boral Limited is comparatively high
volatised than the Hypothecated security secondly the expected return from said
security is higher than the Hypothecated shares. The primary reason for the weak
performance of Hypothecated share is a lack of volatility and weak performance due
to safe and secured investment. Moreover the return of portfolio is consisting high
weightage of return as compare to Hypothecated security option.
8 | P a g e
(Fernandez, P. (2014).
Market Risk premium: the fourth important component of the CAPM model is the
market risk premiums, such premium is computed by formulating the expected return
of the market less the risk free rate. Such marker risk premium presents the additional
return over and above the risk free rate. (Corporate Finance Institute. (2019).
Now in current case:
our selected corporate operate with the beta of 1.14 % during the last five financial
year, this similar indicates that a security of Boral Limited may be vary by nearly 114
%, from the prevailing market price and actual return will be vary by 1.14 time . The
expected and risk free rate is 1.98 % this rate is the rate of 10 year Australian Security
risk free bonds. While the market risk premiums is 6 % this risk premium is reduced
by the risk free rate, in order to measure the effective rate. The selected security is
comparatively lower riskers than the hypothecated security which own a negative
beta,
the negative beta or beta less than Zero, indicates that an investment relating to market
are possible but such investments are higher risky in nature, the actual return from the
security is comparatively low due to lack of volatility and risk in the security, such
type of beta are normally found in case of Gold and similar investment option when
the possibility for variation in price are comparatively lower than what we can
normally note under the normal circumstance of securities. (Finance.zacks.com.
(2019).
After analysing the performance both the securities which we have selected in the
current case, we can concludes that security of Boral Limited is comparatively high
volatised than the Hypothecated security secondly the expected return from said
security is higher than the Hypothecated shares. The primary reason for the weak
performance of Hypothecated share is a lack of volatility and weak performance due
to safe and secured investment. Moreover the return of portfolio is consisting high
weightage of return as compare to Hypothecated security option.
8 | P a g e

References
Corporate Finance Institute. (2019). what is CAPM - Capital Asset Pricing Model -
Formula, Example. Available at:
https://corporatefinanceinstitute.com/resources/knowledge/finance/what-is-capm-
formula/ [Accessed 17 Apr. 2019].
Fernandez, P. (2014). CAPM: UN model absurd (CAPM: An Absurd Model). SSRN
Electronic Journal.
Finance.zacks.com. (2019). Is a Negative Beta Coefficient More Risky Than a Positive
in the Stock Market? Available at: https://finance.zacks.com/negative-beta-
coefficient-risky-positive-stock-market-7596.html [Accessed 17 Apr. 2019].
King, T. and Lewis, K. (2015). Credit Risk, Liquidity and Lies. Finanace and
Economics Discussion Series, 2015(2012), pp.1-41.
Sobolev, D. and Harvey, N. (2016). Assessing Risk in Graphically Presented Financial
Series. Risk Analysis, 36(12), pp.2216-2232.
9 | P a g e
Corporate Finance Institute. (2019). what is CAPM - Capital Asset Pricing Model -
Formula, Example. Available at:
https://corporatefinanceinstitute.com/resources/knowledge/finance/what-is-capm-
formula/ [Accessed 17 Apr. 2019].
Fernandez, P. (2014). CAPM: UN model absurd (CAPM: An Absurd Model). SSRN
Electronic Journal.
Finance.zacks.com. (2019). Is a Negative Beta Coefficient More Risky Than a Positive
in the Stock Market? Available at: https://finance.zacks.com/negative-beta-
coefficient-risky-positive-stock-market-7596.html [Accessed 17 Apr. 2019].
King, T. and Lewis, K. (2015). Credit Risk, Liquidity and Lies. Finanace and
Economics Discussion Series, 2015(2012), pp.1-41.
Sobolev, D. and Harvey, N. (2016). Assessing Risk in Graphically Presented Financial
Series. Risk Analysis, 36(12), pp.2216-2232.
9 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





