Task 1 V = 340 sin (50πt − 0.541) Answer Sine wave in form: V =

Task 1
V = 340 sin (50πt − 0.541)
Answer
Sine wave in form:
V = Vm sin (ωt − φ)
has an amplitude of Vm , angular velocity of ω and phase angle (lagging) of φ
radians.
a)
Comparing the given sine wave equation with the standard form, we have:
Amplitude = 340 V
Angular velocity : ω = 50π
frequency : f =
ω
2π = 50π
2π = 25 Hz
Time Period : T =1
f = 1
25 = 0.04 sec
Phase Angle : φ = 0.541 radians (lagging) or=⇒ 0.541 × 180
π = 31◦ (lagging)
b)
When t = 0:
V = 340 sin (50π · 0 − 0.541)
= 340 sin (−0.541) = −175.0978 V
c)
When t = 10 ms:
V = 340 sin (50π · 10−2 − 0.541)
= 340 sin (0.5π − 0.541) = 291.446 V
d)
1

When V = 200 V
200 = 340 sin (50πt − 0.541)
=⇒ sin (50πt − 0.541) =
200
340
50πt − 0.541 = sin−1 200
340
50πt − 0.541 = 0.6289
∴ t = 0.6289 + 0.541
50π = 0.007 sec
The sine wave first reaches 200 V at the time t = 0.007 sec.
e)
Maximum voltage occurs when the sine term of the sine wave is maximum, that
is sin (50πt − 0.541) = 1.Implies,
Vmax = 340 · max[sin (50πt − 0.541)]
| {z }
=1
=⇒ sin (50πt − 0.541) = 1
∴ 50πt − 0.541 = sin−1(1)
[sin−1(1) = π
2 + 2n, where, n = 0, 1, 2, . . . ]
∴ 50πt − 0.541 =
π
2 + 2n
=⇒ t = 1
50π
π
2 + 2n + 0.541
The sine wave first reaches it’s maximum value, when n = 0, that is:
t = 1
50π
π
2 + 0.541 = 0.0134 sec
f )
The given sine function is plotted using a graphing calculator (Desmos).The
y-axis is scaled by a factor of10000,so 1 unit which is seen to be 0.005 V
actually represents 50 V.
2

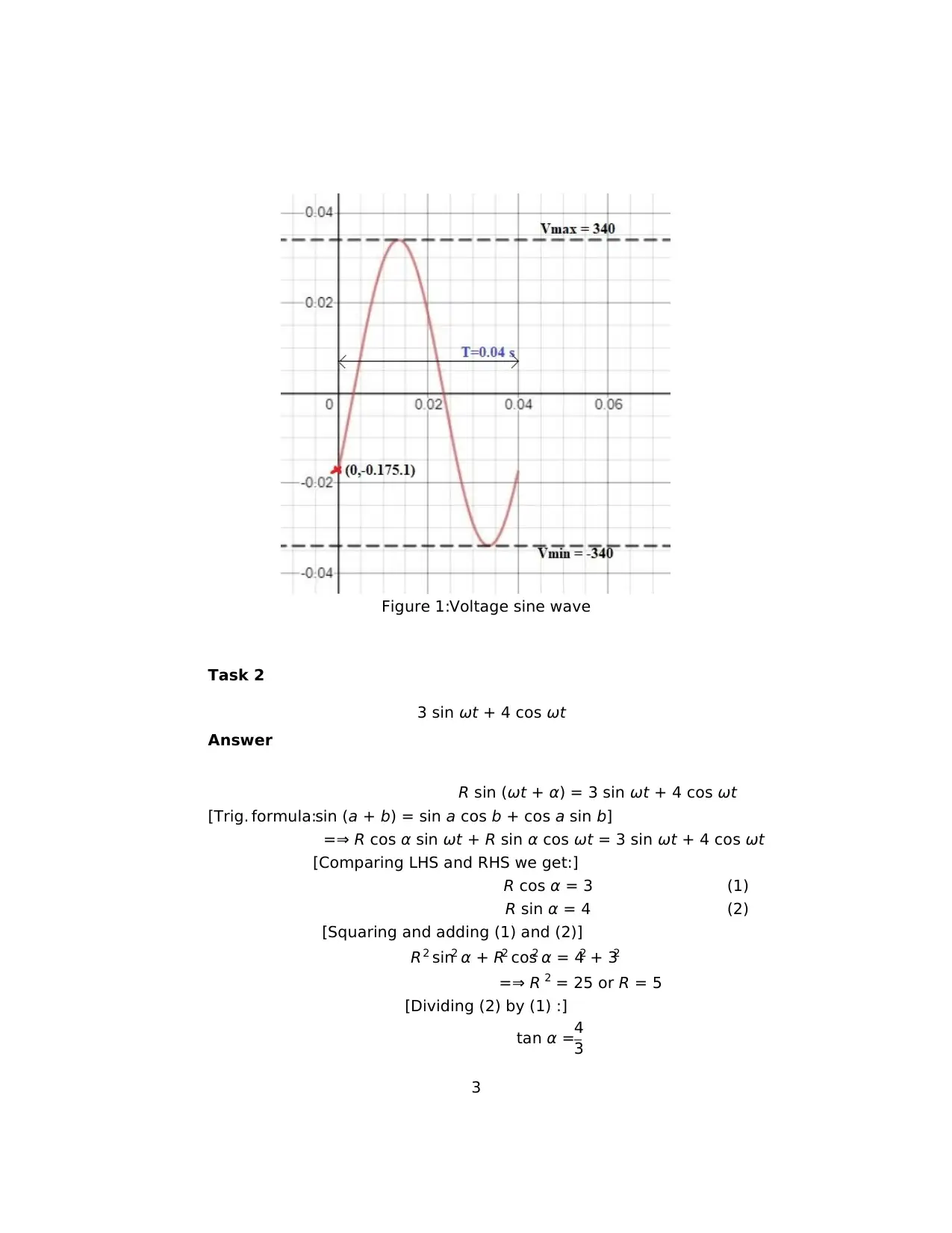
Figure 1:Voltage sine wave
Task 2
3 sin ωt + 4 cos ωt
Answer
R sin (ωt + α) = 3 sin ωt + 4 cos ωt
[Trig. formula:sin (a + b) = sin a cos b + cos a sin b]
=⇒ R cos α sin ωt + R sin α cos ωt = 3 sin ωt + 4 cos ωt
[Comparing LHS and RHS we get:]
R cos α = 3 (1)
R sin α = 4 (2)
[Squaring and adding (1) and (2)]
R2 sin2 α + R2 cos2 α = 42 + 32
=⇒ R 2 = 25 or R = 5
[Dividing (2) by (1) :]
tan α =4
3
3

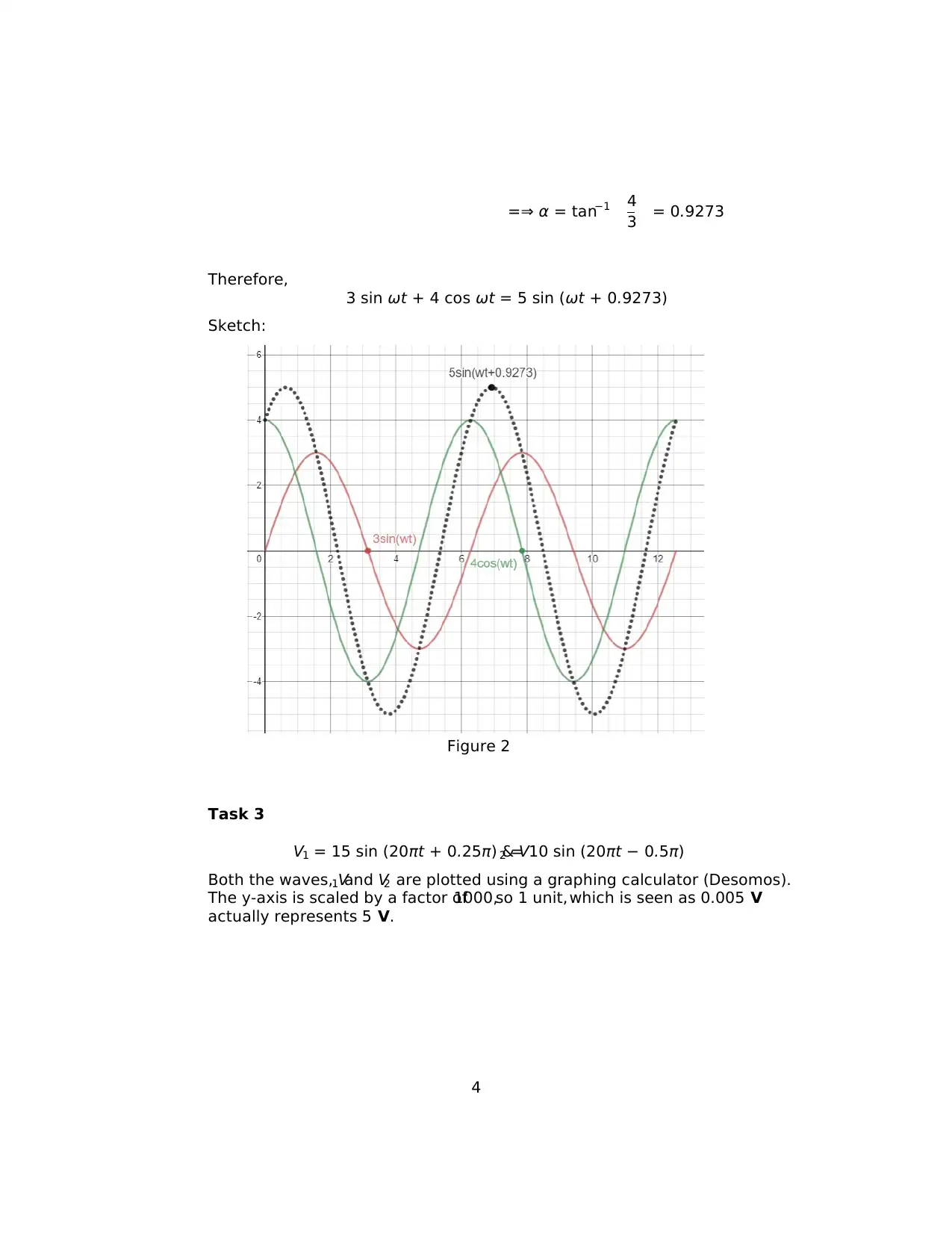
=⇒ α = tan−1 4
3 = 0.9273
Therefore,
3 sin ωt + 4 cos ωt = 5 sin (ωt + 0.9273)
Sketch:
Figure 2
Task 3
V1 = 15 sin (20πt + 0.25π) & V2 = 10 sin (20πt − 0.5π)
Both the waves, V1 and V2 are plotted using a graphing calculator (Desomos).
The y-axis is scaled by a factor of1000,so 1 unit,which is seen as 0.005 V
actually represents 5 V.
4

Figure 3:Addition of two waves graphically
Figure 4:Resultant sine wave
Figure 3 shows the addition of waves V1 and V2 graphically.The resultant wave
V1 + V2 is again shown separately in figure-4.
1) From figure-4 it is clear that the resultant wave, V1 +V2 too has a time period:
T = 0.01s, which is same as that of the component waves V1 and V2. Thus the
resultant wave also has an angular velocity:ω = 20π.
2) The amplitude of resulting wave can be seen as 10.6 V.
3) It is seen that the wave leads with a phase of 0.00091s.Now, as T = 0.1s
corresponds to an angle of 2π, then phase angle corresponding to 0.00091s is:
0.00091
0.1 × 2π = 0.057 rads
Summary of results obtained from figure-4:
T = 0.01 s,ω = 20π,Amp. = A = 10.6 V,φ = 0.057
5

When these values are plugged into the standard equation for sine waves:
V = A sin (ωt + φ)
then the equation for resulting wave is:
V1 + V2 = 10.6 sin (20πt + 0.057)
Obtaining the resultant wave equation using trigonometric manipulation:
R sin (ωt + α) = 15 sin (ωt + 0.25π) + 10 sin (ωt − 0.5π)
[Trig. formula:sin (a ± b) = sin a cos b ± cos a sin b]
∴ R cos α sin ωt + R sin α cos ωt = 15 cos (0.25π) sin ωt + 15 sin (0.25π) cos ω
+ 10 cos (0.5π) sin ωt − 10 sin (0.5π) cos ωt
= 10.6 sin ωt + 10.6 cos ωt − 10 cos ωt
[Comparing LHS and RHS]
R cos α = 10.6 (1)
R sin α = 0.6 (2)
[Squaring and adding (1) and (2)]
R2 sin2 α + R2 cos2 α = 10.62 + 0.62
=⇒ R 2 = 112.72 or R = 10.62 ≈ 10.6
[Dividing (2) by (1) ]
tan α = 0.6
10.6
=⇒ α = tan−1 0.6
10.6 = 0.057 rads
Substituting R = 10.6, ω = 20π and α = 0.057 in the resultant wave equation,
we get:
R sin (ωt + α) = 10.6 sin (20πt + 0.057)
This is same as the result obtained from graphical analysis.
Task 4
F1 = h2, −1, 1ir1 = h3, 1, 5i
F2 = h8, −6, 6ir2 = h5, −2, −1i
F3 = h4, 0, 3ir3 = h1, −6, 7i
F4 = h1, −5, 0ir4 = h1, 0, 6i
6

Answer
The equilibrium of a body is determined by the condition:
(r1 × F1) + (r2 × F2) + (r3 × F3) + (r4 × F4) = 0
Substituting the given force and position vectors in the LHS of the above equa-
tion:
(h3, 1, 5i×h2, −1, 1i)+(h5, −2, −1i×h8, −6, 6i)+(h1, −6, 7i×h4, 0, 3i)+(h1, 0, 6i×h1, −5, 0i)
First carry out the cross products individually and then add the results:
h3, 1, 5i × h2, −1, 1i =
ˆi ˆj ˆk
3 1 5
2 −1 1
= (1 + 5)ˆi − (3 − 10)ˆj + (−3 − 2)ˆk
= h6, 7, −5i
h5, −2, −1i × h8, −6, 6i =
ˆi ˆj ˆk
5 −2 −1
8 −6 6
= (−12 − 6)ˆi − (30 + 8)ˆj + (−30 + 16)ˆk
= h−18, −38, −14i
h1, −6, 7i × h4, 0, 3i =
ˆi ˆj ˆk
1 −6 7
4 0 3
= (−18 − 0)ˆi − (3 − 28)ˆj + (0 + 24)ˆk
= h−18, 25, 24i
h1, 0, 6i × h1, −5, 0i =
ˆi ˆj ˆk
1 0 6
1 −5 0
= (0 + 30)ˆi − (0 − 6)ˆj + (−5 + 0)ˆk
= h30, 6, −5i
Adding all the results together:
(h3, 1, 5i × h2, −1, 1i) + (h5, −2, −1i × h8, −6, 6i)+
(h1, −6, 7i × h4, 0, 3i) + (h1, 0, 6i × h1, −5, 0i) = h6, 7, −5i + h−18, −38, −14i+
h−18, 25, 24i + h30, 6, −5i
= h6 − 18 − 18 + 30, 7 − 38 + 25 + 6, −5 − 14 + 2
= h0, 0, 0i
7

Thus, the equilibrium condition is satisfied and the body seems to maintain
equilibrium under the given condition.
References:
Ayres, F. and Mendelson, E. (2013).Calculus.New York:McGraw-Hill.
Haykin,S. (2014).Digitalcommunication systems.Hoboken,NJ: J. Wiley &
Sons.
8