Analysis of Temperature and Humidity Data for Melbourne in 2017

The analysis includes the use of MATLAB to generate random temperature and humidity data, fitting normal distribution curves, and calculating parameters. Linear regression and interpolation techniques are used to predict the maximum temperature on 29th October 2017. The data is collected from the Bureau of Meteorology and Timeanddate.com.

Question 4:
In this question the random seed for generating the random 3 pm temperatures and the 9 am
temperatures are taken as seed = 0.7558.
Now, the minimum temperature in July at 3 pm as obtained from the Bureau of Meteorology
is 20.9 °C and maximum temperature is 24.9 °C. Also, the average humidity at July at 9 am is
71% (Timeanddate.com 2018).
MATLAB code:
s = 0.7558;
rng(s);
T3 = (24.9-20.9).*rand(10,1) + 20.9
T3 =
21.5305
24.7824
24.7287
22.8415
24.1011
21.4675
22.5870
24.5629
24.0688
24.7380
Now, the first 10 values of humidity is generated by the following code.
rng(s)
>> phi9 = 71 + 2.*randn(10,1)
phi9 =
72.0753
74.6678
66.4823
72.7243
71.6375
68.3846
70.1328
71.6852

78.1568
76.5389
Now, the sample mean and standard deviation for T3 and phi9 are calculated as follows.
mean(T3)
ans =
23.5408
std(T3)
ans =
1.3234
mean(phi9)
ans =
72.2486
std(phi9)
ans =
3.5398
Now, the similar process is followed to generate the first 20 data values for T3 and phi9.
rng(s)
T3 = (24.9-20.9).*rand(20,1) + 20.9
rng(s)
phi9 = 71 + 2.*randn(20,1)
Now, the parameters of the two variables are calculated as follows.
mean(phi9)
ans =
72.3292
std(phi9)
ans =
2.9594
Now, normal distributed is fitted with phi9 which is shown by the histogram of the data along
with the normally fitted line.
histfit(phi9)

62 64 66 68 70 72 74 76 78 80 82
0
1
2
3
4
5
6
7
Similarly, the variable T3 is also fitted with normal distribution and the parameters are shown
below (In.mathworks.com 2018).
Normal distribution
mu = 23.4681 [22.8505, 24.0858]
sigma = 1.31973 [1.00364, 1.92756]
The 95% confidence levels are shown in the brackets.

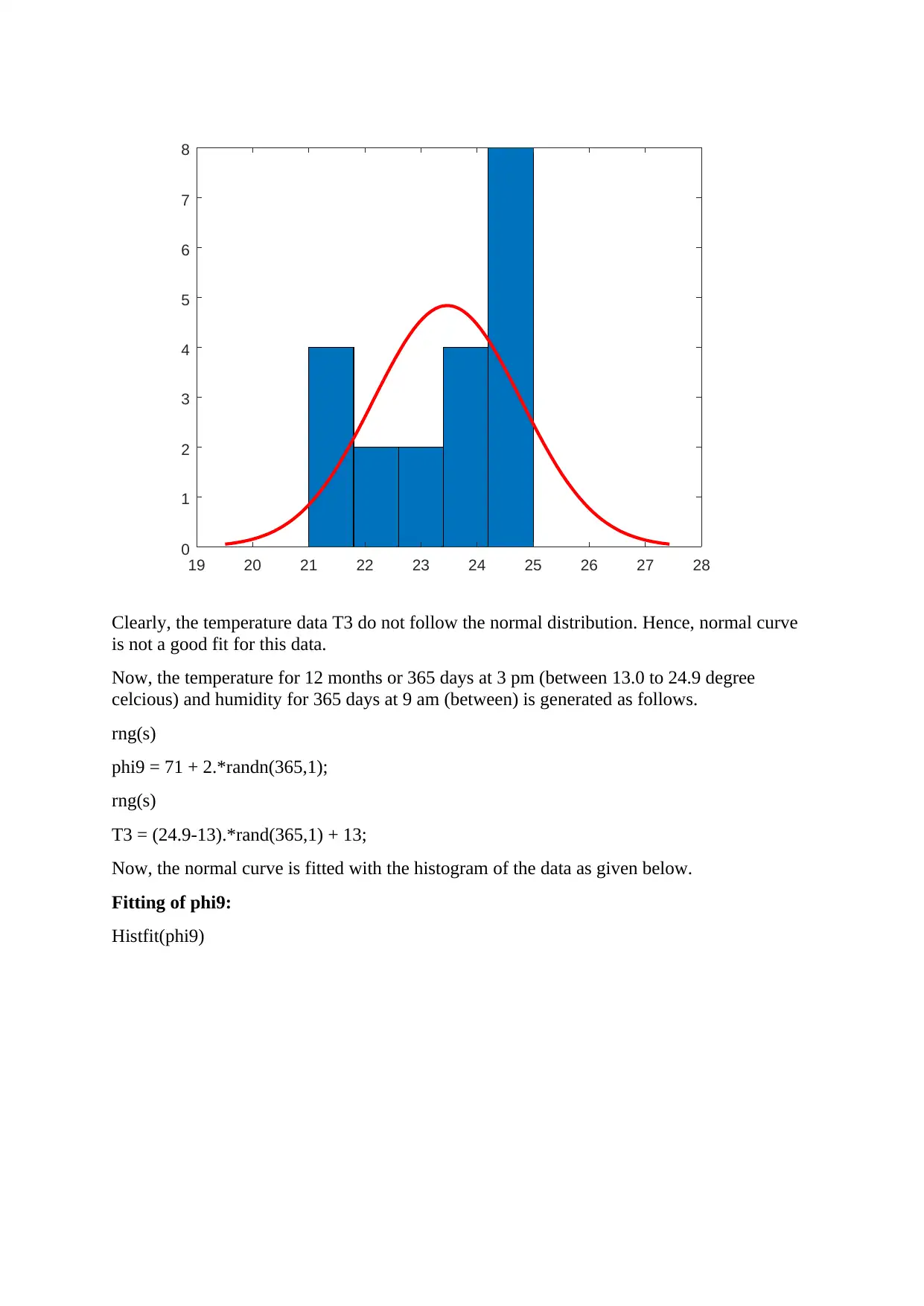
19 20 21 22 23 24 25 26 27 28
0
1
2
3
4
5
6
7
8
Clearly, the temperature data T3 do not follow the normal distribution. Hence, normal curve
is not a good fit for this data.
Now, the temperature for 12 months or 365 days at 3 pm (between 13.0 to 24.9 degree
celcious) and humidity for 365 days at 9 am (between) is generated as follows.
rng(s)
phi9 = 71 + 2.*randn(365,1);
rng(s)
T3 = (24.9-13).*rand(365,1) + 13;
Now, the normal curve is fitted with the histogram of the data as given below.
Fitting of phi9:
Histfit(phi9)

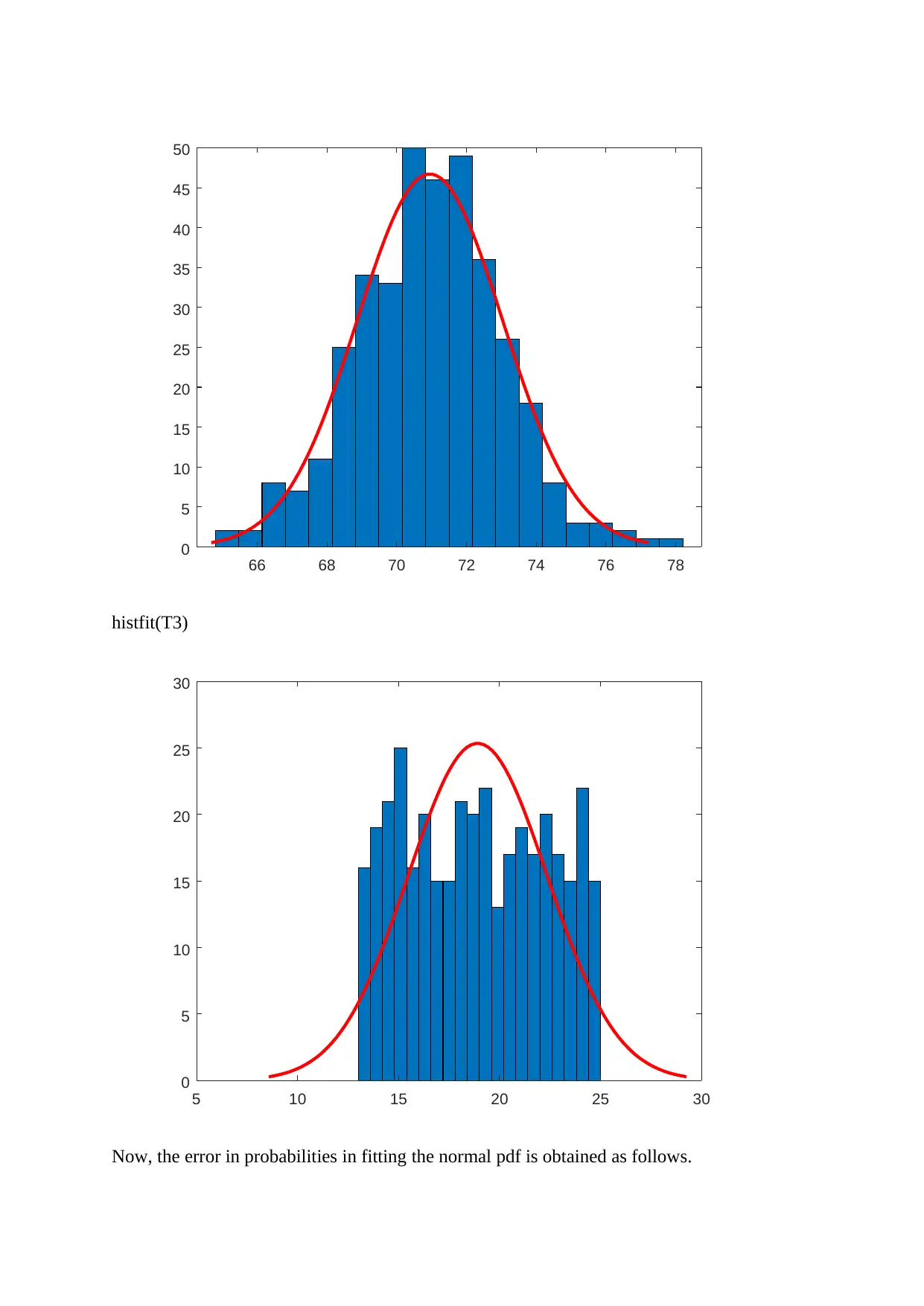
66 68 70 72 74 76 78
0
5
10
15
20
25
30
35
40
45
50
histfit(T3)
5 10 15 20 25 30
0
5
10
15
20
25
30
Now, the error in probabilities in fitting the normal pdf is obtained as follows.

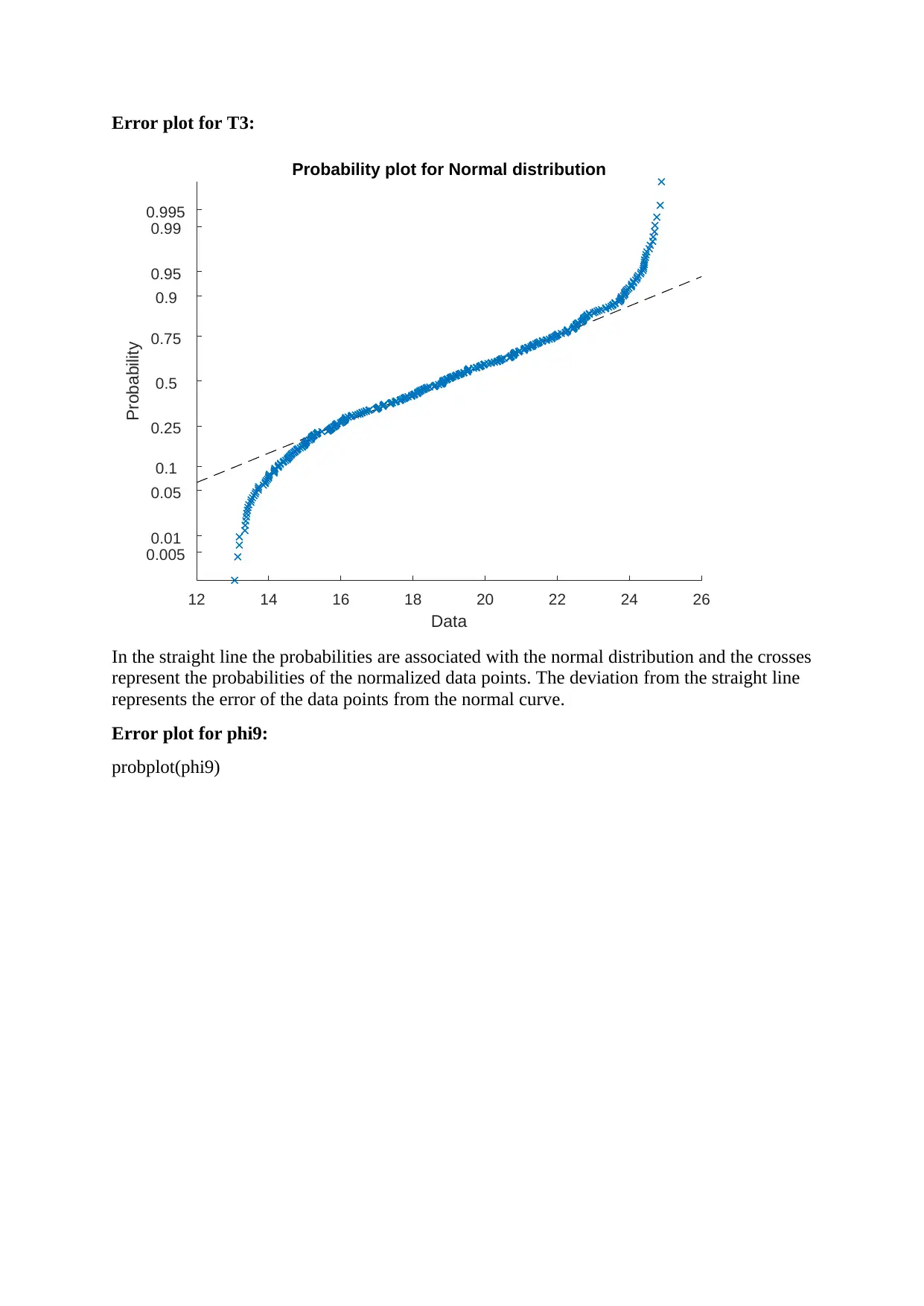
Error plot for T3:
12 14 16 18 20 22 24 26
Data
0.005
0.01
0.05
0.1
0.25
0.5
0.75
0.9
0.95
0.99
0.995
Probability
Probability plot for Normal distribution
In the straight line the probabilities are associated with the normal distribution and the crosses
represent the probabilities of the normalized data points. The deviation from the straight line
represents the error of the data points from the normal curve.
Error plot for phi9:
probplot(phi9)

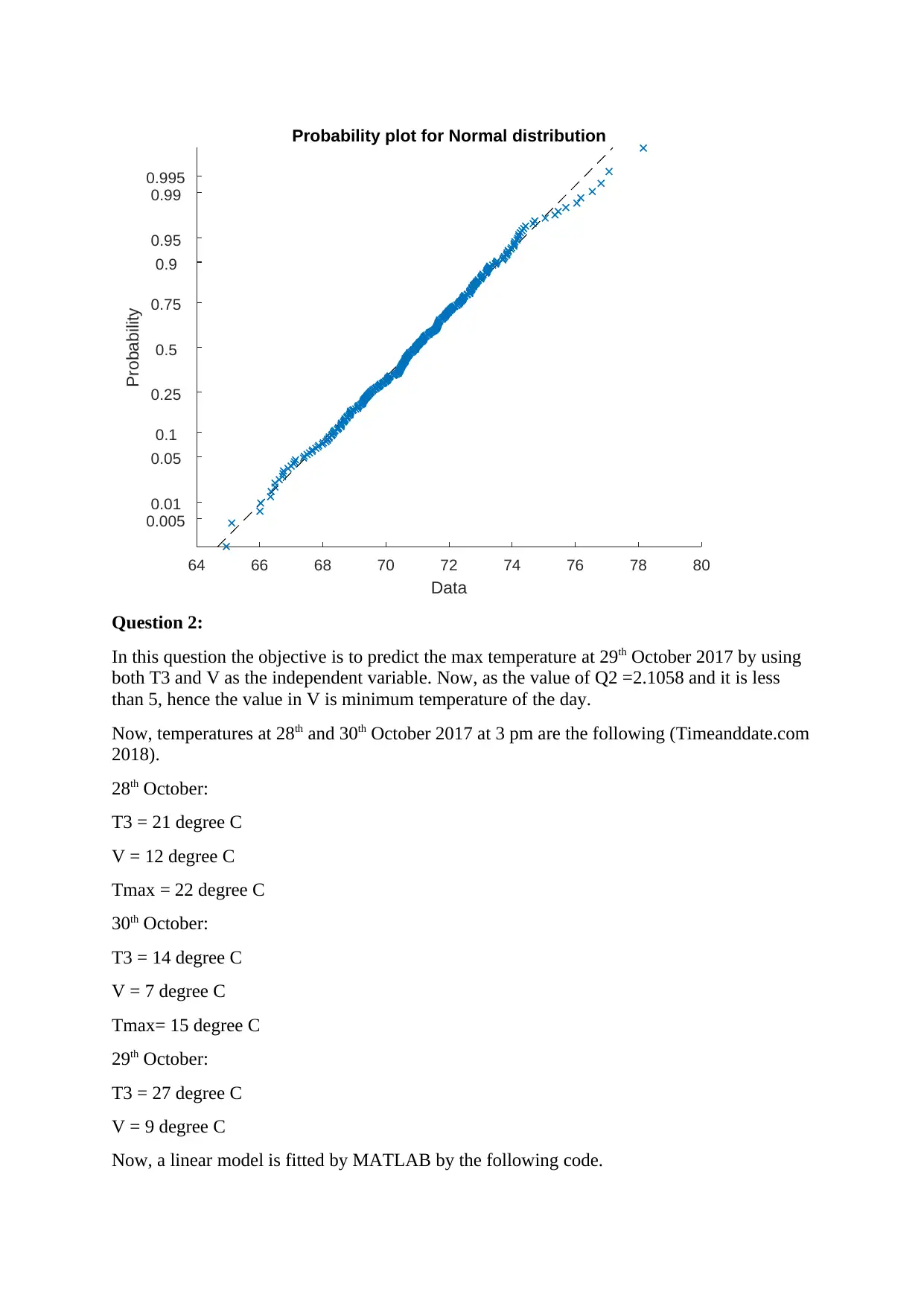
64 66 68 70 72 74 76 78 80
Data
0.005
0.01
0.05
0.1
0.25
0.5
0.75
0.9
0.95
0.99
0.995
Probability
Probability plot for Normal distribution
Question 2:
In this question the objective is to predict the max temperature at 29th October 2017 by using
both T3 and V as the independent variable. Now, as the value of Q2 =2.1058 and it is less
than 5, hence the value in V is minimum temperature of the day.
Now, temperatures at 28th and 30th October 2017 at 3 pm are the following (Timeanddate.com
2018).
28th October:
T3 = 21 degree C
V = 12 degree C
Tmax = 22 degree C
30th October:
T3 = 14 degree C
V = 7 degree C
Tmax= 15 degree C
29th October:
T3 = 27 degree C
V = 9 degree C
Now, a linear model is fitted by MATLAB by the following code.

MATLAB code:
T3 =[21,14]; Tmax =[22,15]; V =[12,7];
T =[T3;V;Tmax]';
T = array2table(T, 'VariableNames', {'T3', 'V','Tmax'})
T =
2×3 table
T3 V Tmax
__ __ ____
21 12 22
14 7 15
model = fitlm(T,'Tmax~T3+V')
model =
Linear regression model:
Tmax ~ 1 + T3 + V
Estimated Coefficients:
Estimate SE tStat pValue
________ __ _____ ______
(Intercept) 0 0 NaN NaN
T3 1.2381 0 Inf NaN
V -0.33333 0 -Inf NaN
Number of observations: 2, Error degrees of freedom: 0
R-squared: 1, Adjusted R-Squared NaN
F-statistic vs. constant model: NaN, p-value = NaN
Hence, the least square model is
Tmax = 1.2381*T3 -0.33*V
Now, from this model the max temperature in 29th October is
Tmax = 1.2381*27 – 0.33*9 = 30.4587 degree C.

Now, after collecting the data file for all the days in year 2017 the same analysis can be
performed and the regression model can be formed for the year and the errors can be
obtained.
Question 3:
Now, in this case the linear interpolation technique is used to find the maximum temperature
on 29th October 2017 as given below (In.mathworks.com 2018). At first time t as the
independent variable is used. Then V is used as independent variable where V = Tmin as Q3
is less than or equals to 5.
Now, t is starting from 0 from 19th October and hence on 29th October t = 10, on 28th October
t = 9 and on 30th October t = 11.
Now, Tmax(9) = 21 degree C.
V(9) = 12 degree C.
V(10) = 9 degree C.
Tmax(11) = 15 degree C.
V(11) = 7 degree C.
Now, first the independent variable is t.
Hence, (Tmax(10) – Tmax(9))/(10- 9) = (Tmax(11) – Tmax(9))/(11 – 9)
 (Tmax(10) – 21) = (15-21)/(2)
 Tmax(10) = 21- 3 = 18 degree C.
Now, taking V= Tmin is the independent variable
(Tmax(10) – Tmax(9))/(V(10)- V(9)) = (Tmax(11) – Tmax(9))/(V(11) – V(9))
 (Tmax(10) – 21)/(9-12) = (15-21) /(7- 12)
 Tmax(10) = -3*(6/5) + 21 =>Tmax(10)= 17.4 degree C.
Hence, two independent variables produce two approximately same results.
Now, the method of cubic spline is applied to find the Tmax on 29th October.
The values from 19th October to 31st October are as follows (Timeanddate.com 2018).
Tmax(0) = 25 degree C, V(0) = 11 degree C
Tmax(1) = 16, V(1) = 8
Tmax(2) = 15, V(2) = 10
Tmax(3) = 16, V(3) = 10
Tmax(4) = 20, V(4) = 10
Tmax(5) = 22, V(5) = 9
Tmax(6) = 17, V(6) = 13
Tmax(7) = 16, V(7) = 11
Tmax(8) = 27, V(8) = 12

Tmax(9) = 22, V(9) = 12
V(10) = 9
Tmax(11) = 15, V(11) = 7
Tmax(12) = 15, V(12) = 5
MATLAB code for spline method:
t = [0 1 2 3 4 5 6 7 8 9 11 12];
>> Tmax =[25 16 15 16 20 22 17 16 27 22 15 15];
>> V =[11 8 10 10 10 9 13 11 12 12 7 5];
>> maxT =spline(t,Tmax,10)
maxT =
16.5383
Hence, the maximum temperature on 29th October is 16.5383 degree Celsius by cubic spline
method.

References:
Timeanddate.com. (2018). Weather for Melbourne, Victoria, Australia. [online] Available at:
https://www.timeanddate.com/weather/australia/melbourne [Accessed 8 Oct. 2018].
In.mathworks.com. (2018). Cubic spline data interpolation - MATLAB spline- MathWorks
India. [online] Available at: https://in.mathworks.com/help/matlab/ref/spline.html [Accessed
8 Oct. 2018].
In.mathworks.com. (2018). Create linear regression model - MATLAB fitlm- MathWorks
India. [online] Available at: https://in.mathworks.com/help/stats/fitlm.html [Accessed 8 Oct.
2018].