Bending Moment Diagram for Different Load Cases

This document explains how to create a bending moment diagram for different load cases using MATLAB. It provides the equations and code for each load case, along with the resulting reactions and moments. The document also includes a comparison plot of all the bending moment diagrams.

THE COURSEWORK
Name of the Student
Name of the University
Author’s Note
1 | P a g e

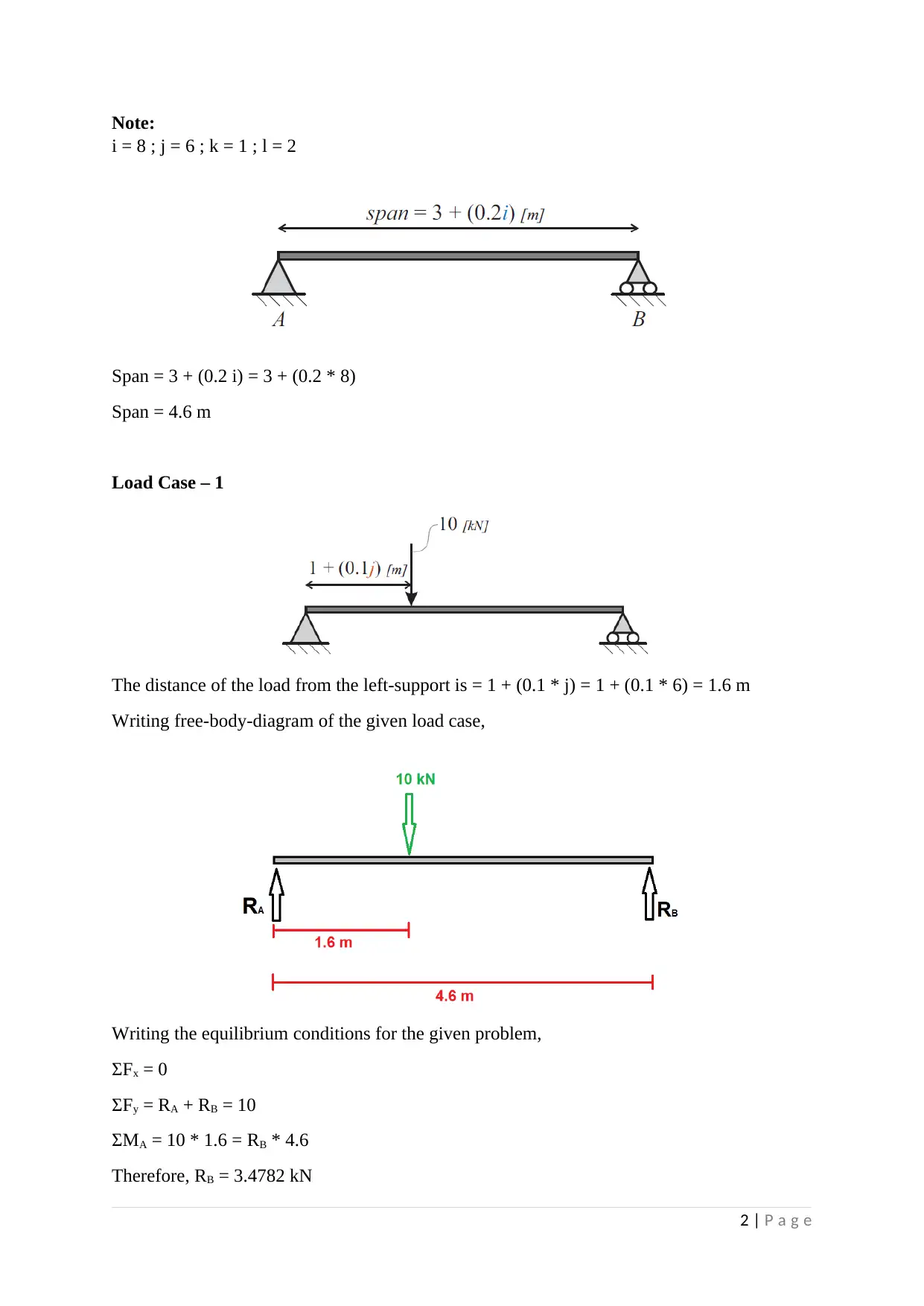
Note:
i = 8 ; j = 6 ; k = 1 ; l = 2
Span = 3 + (0.2 i) = 3 + (0.2 * 8)
Span = 4.6 m
Load Case – 1
The distance of the load from the left-support is = 1 + (0.1 * j) = 1 + (0.1 * 6) = 1.6 m
Writing free-body-diagram of the given load case,
Writing the equilibrium conditions for the given problem,
ƩFx = 0
ƩFy = RA + RB = 10
ƩMA = 10 * 1.6 = RB * 4.6
Therefore, RB = 3.4782 kN
2 | P a g e

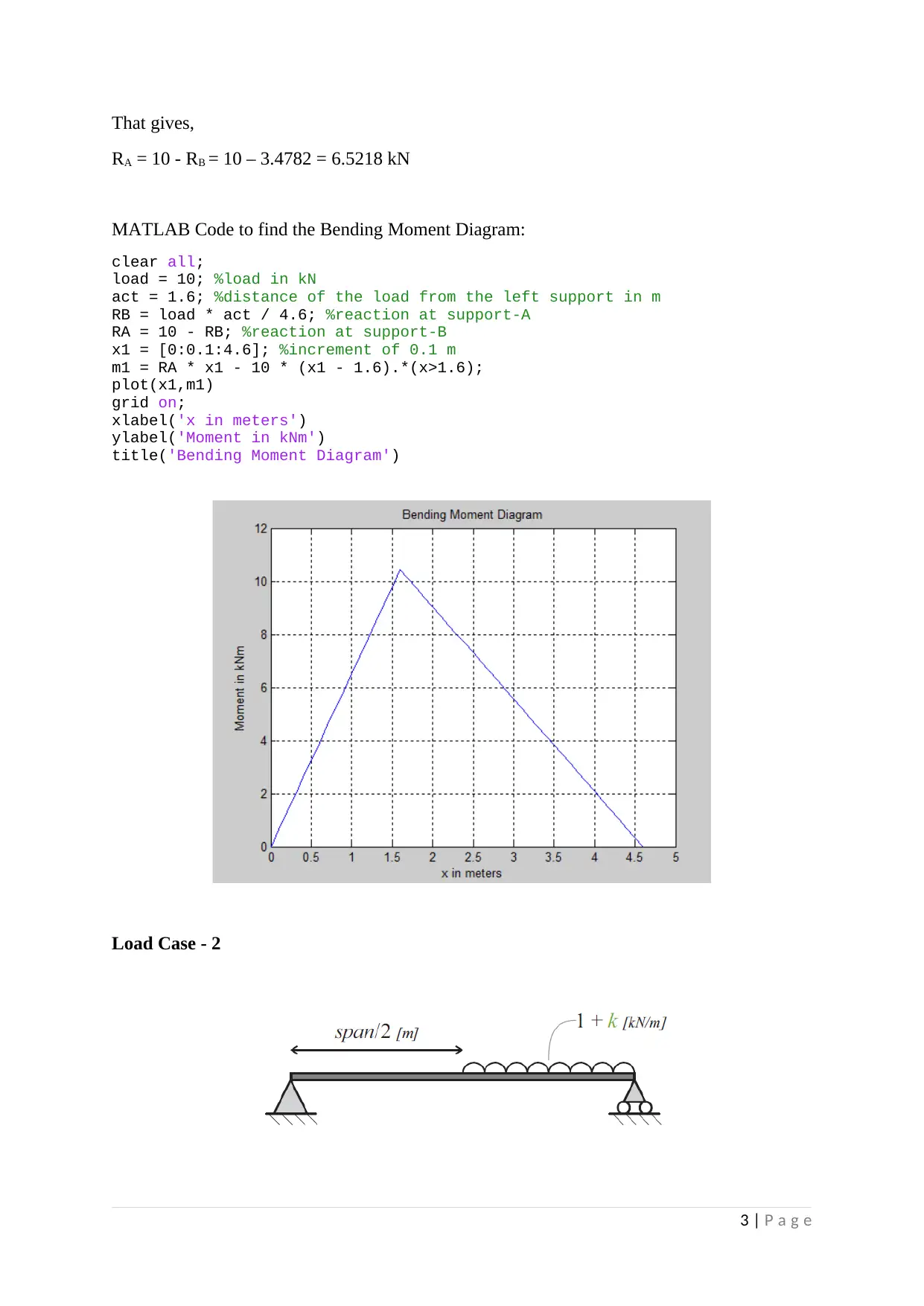
That gives,
RA = 10 - RB = 10 – 3.4782 = 6.5218 kN
MATLAB Code to find the Bending Moment Diagram:
clear all;
load = 10; %load in kN
act = 1.6; %distance of the load from the left support in m
RB = load * act / 4.6; %reaction at support-A
RA = 10 - RB; %reaction at support-B
x1 = [0:0.1:4.6]; %increment of 0.1 m
m1 = RA * x1 - 10 * (x1 - 1.6).*(x>1.6);
plot(x1,m1)
grid on;
xlabel('x in meters')
ylabel('Moment in kNm')
title('Bending Moment Diagram')
Load Case - 2
3 | P a g e

The value of 1 + k = 1 + 1 = 2
The resulting case will be:
Writing free-body-diagram of the given load case, (and converting uniformly distributive
load to point-load)
Writing the equilibrium conditions for the given problem,
ƩFx = 0
ƩFy = RA + RB = 4.6
ƩMA = 4.6 * 3.45 = RB * 4.6
Therefore, RB = 3.45 kN
That gives,
RA = 4.6 - RB = 4.6 – 3.45 = 1.15 kN
MATLAB Code to find the Bending Moment Diagram:
clear all;
load = 4.6; %load in kN
act = 3.45; %distance of the load from the left support in m
RB = load * act / 4.6; %reaction at support-A
RA = 4.6 - RB; %reaction at support-B
x1 = [0:0.1:4.6]; %increment of 0.1 m
m1 = RA * x1 - 4.6 * (x1 - 3.45).*(x1>3.45);
plot(x1,m1)
grid on;
xlabel('x in meters')
ylabel('Moment in kNm')
title('Bending Moment Diagram')
4 | P a g e

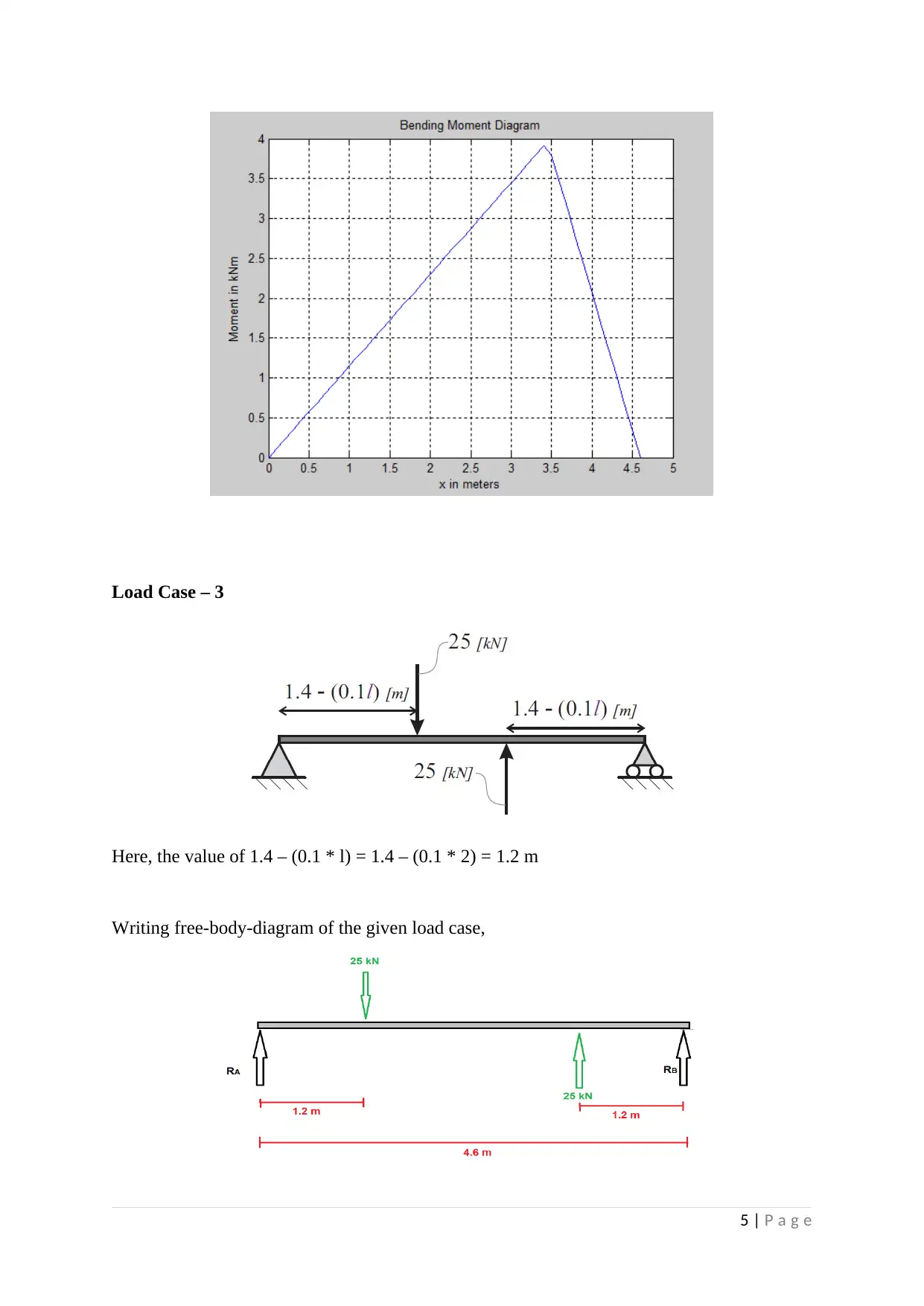
Load Case – 3
Here, the value of 1.4 – (0.1 * l) = 1.4 – (0.1 * 2) = 1.2 m
Writing free-body-diagram of the given load case,
5 | P a g e

Writing the equilibrium conditions for the given problem,
ƩFx = 0
ƩFy = RA + RB + 25 = 25
ƩMA = 25 * 1.2 = 25 * 3.4 + RB * 4.6
Therefore, RB = -11.956 kN
That gives,
RA = - RB = 11.956 kN
MATLAB Code to find the Bending Moment Diagram:
clear all;
load1 = 25; %load_1 in kN
act1 = 1.2; %distance of the load_1 from the left support in m
load2 = -25; %load_2 in kN
act2 = 3.4; %distance of the load_2 from the left support in m
%support reactions
RB = (load1 * act1 + load2 * act2)/ 4.6; %reaction at support-A
RA = - RB %reaction at support-B
%To find moments
x1 = [0:0.1:1.2];
m1 = RA * x1;
x2 = [1.2:0.1:3.4];
m2 = RA * x2 - 25 * (x2 - 1.2);
x3 = [3.4:0.1:4.6];
m3 = RA * x3 - 25 * (x3 - 1.2) + 25 * (x3 -3.4);
x = [x1,x2,x3];
m = [m1,m2,m3];
plot(x,m)
grid on;
xlabel('x in meters')
ylabel('Moment in kNm')
title('Bending Moment Diagram')
6 | P a g e

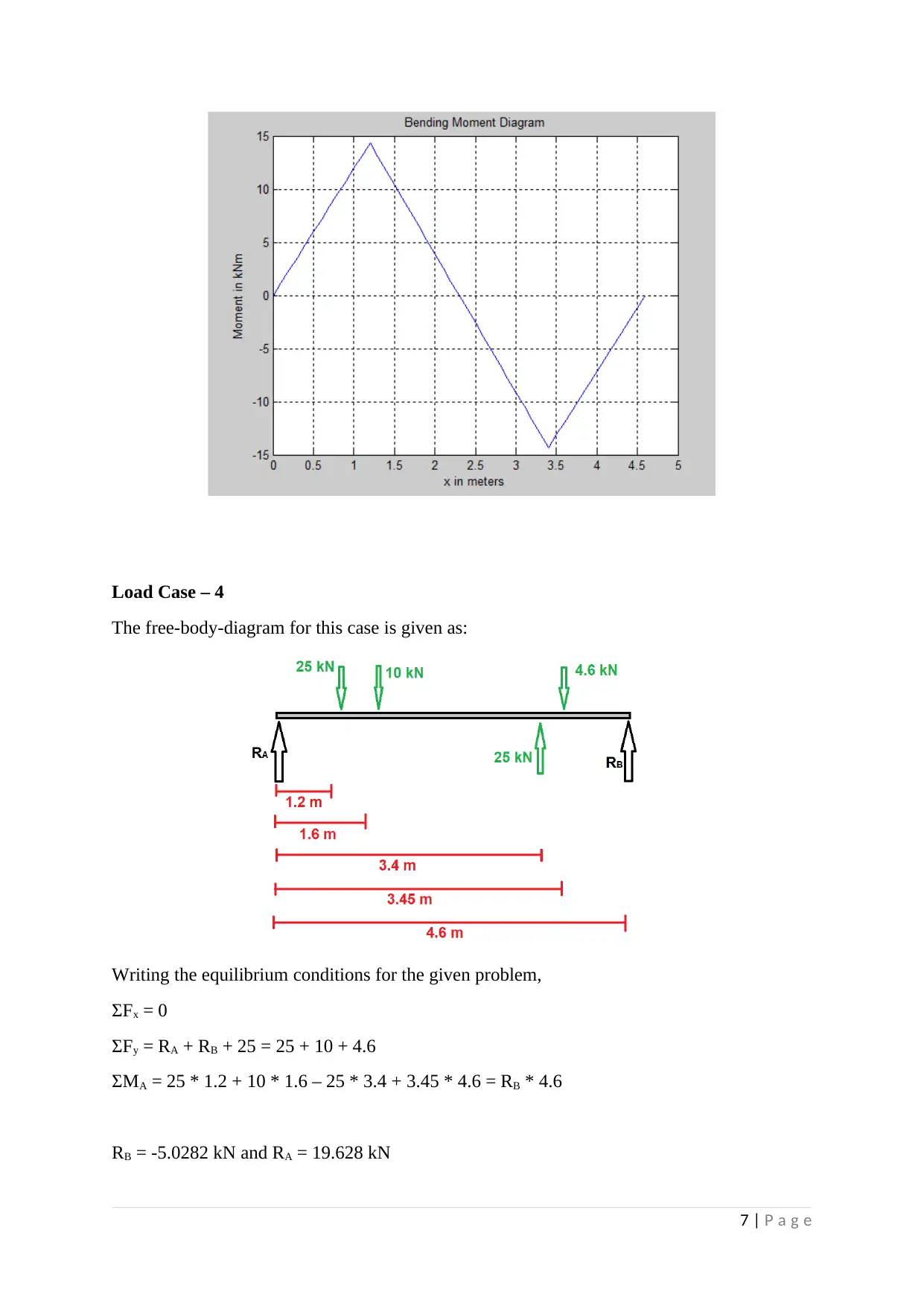
Load Case – 4
The free-body-diagram for this case is given as:
Writing the equilibrium conditions for the given problem,
ƩFx = 0
ƩFy = RA + RB + 25 = 25 + 10 + 4.6
ƩMA = 25 * 1.2 + 10 * 1.6 – 25 * 3.4 + 3.45 * 4.6 = RB * 4.6
RB = -5.0282 kN and RA = 19.628 kN
7 | P a g e

MATLAB Code to find the Bending Moment Diagram:
clear all;
load1 = 25; %load_1 in kN
load2 = 10; %load_2 in kN
load3 = -25; %load_3 in kN
load4 = 4.6; %load_4 in kN
act1 = 1.2;
act2 = 1.6;
act3 = 3.4;
act4 = 3.45;
%support reactions
RB = (load1 * act1 + load2 * act2 + load3 * act3 + load4 * act4) / 4.6
%reaction at support-A
RA = 14.6 - RB %reaction at support-B
%To find moments
x1 = [0:0.1:1.2];
m1 = RA * x1;
x2 = [1.2:0.1:1.6];
m2 = RA * x2 - 25 * (x2 - 1.2);
x3 = [1.6:0.1:3.4];
m3 = RA * x3 - 25 * (x3 - 1.2) - 10 * (x3 - 1.6);
x4 = [3.4:0.1:3.45];
m4 = RA * x4 - 25 * (x4 - 1.2) - 10 * (x4 - 1.6) + 25 * (x4 - 3.4);
x5 = [3.45:0.1:4.6];
m5 = RA * x5 - 25 * (x5 - 1.2) - 10 * (x5 - 1.6) + 25 * (x5 - 3.4) -
4.6 * (x5 - 3.45);
x = [x1,x2,x3,x4,x5];
m = [m1,m2,m3,m4,m5];
plot(x,m)
grid on;
xlabel('x in meters')
ylabel('Moment in kNm')
title('Bending Moment Diagram')
8 | P a g e

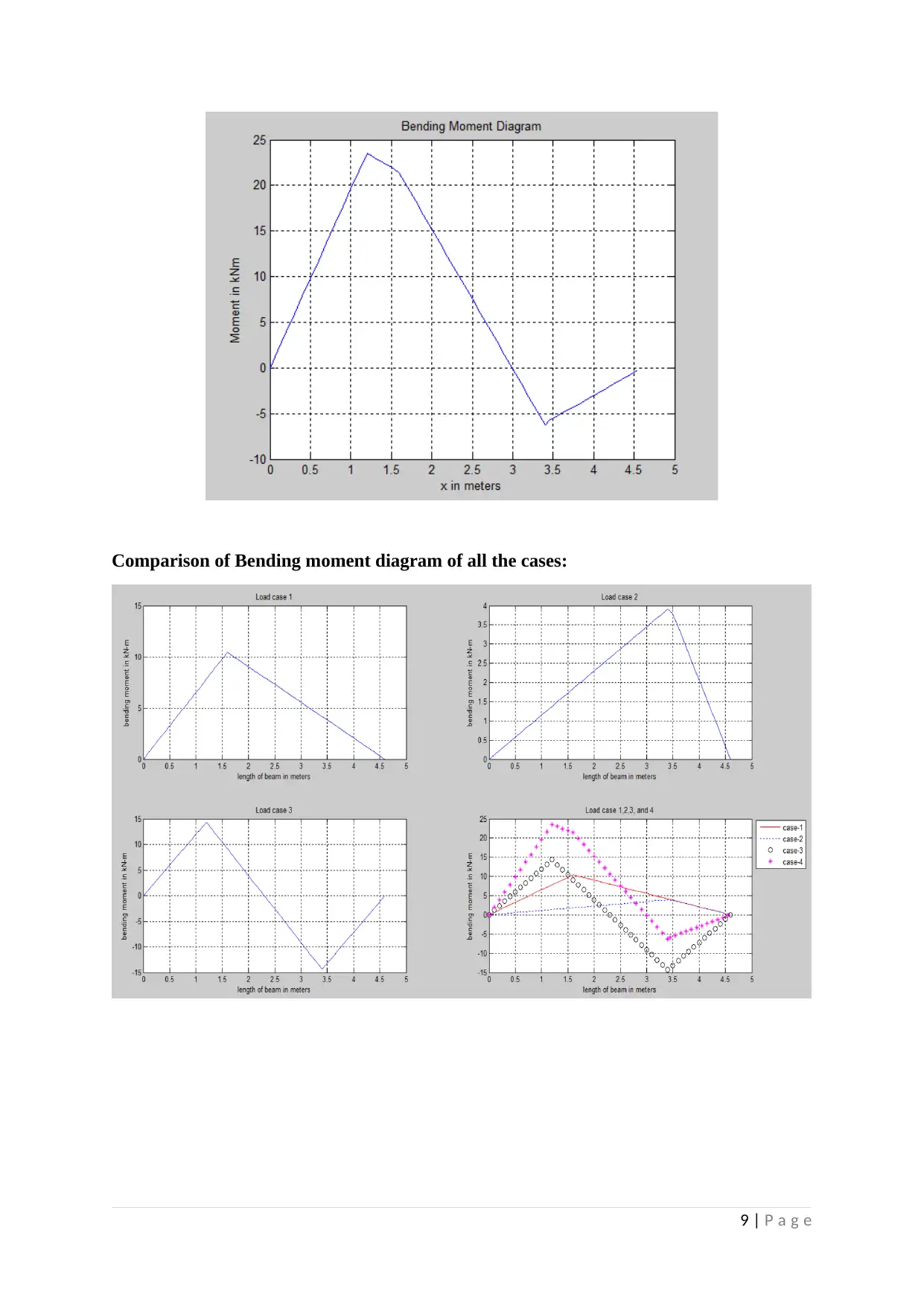
Comparison of Bending moment diagram of all the cases:
9 | P a g e

MATLAB Code for the comparison plot:
clear all;
%for case_1
load = 10; %load in kN
act = 1.6; %distance of the load from the left support in m
RBc1 = load * act / 4.6; %reaction at support-A
RAc1 = 10 - RBc1; %reaction at support-B
xc1 = [0:0.1:4.6]; %increment of 0.1 m
mc1 = RAc1 * xc1 - 10 * (xc1 - 1.6).*(xc1>1.6); %moment for case_1
subplot(2,2,1)
plot(xc1,mc1)
grid on;
xlabel('length of beam in meters')
ylabel('bending moment in kN-m')
title('Load case 1')
%for case_2
loadc2 = 4.6; %load in kN
act = 3.45; %distance of the load from the left support in m
RBc2 = loadc2 * act / 4.6; %reaction at support-A
RAc2 = 4.6 - RBc2; %reaction at support-B
xc2 = [0:0.1:4.6]; %increment of 0.1 m
mc2 = RAc2 * xc2 - 4.6 * (xc2 - 3.45).*(xc2>3.45);%moment for case_2
subplot(2,2,2)
plot(xc2,mc2)
grid on;
xlabel('length of beam in meters')
ylabel('bending moment in kN-m')
title('Load case 2')
%for case_3
load1c3 = 25; %load_1 in kN
act1c3 = 1.2; %distance of the load_1 from the left support in m
load2c3 = -25; %load_2 in kN
act2c3 = 3.4;%distance of the load_2 from the left support in m
RBc3 = (load1c3 * act1c3 + load2c3 * act2c3)/ 4.6; %reaction at support-A
RAc3 = - RBc3; %reaction at support-B
%To find moments
x1c3 = [0:0.1:1.2];
m1c3 = RAc3 * x1c3;
x2c3 = [1.2:0.1:3.4];
m2c3 = RAc3 * x2c3 - 25 * (x2c3 - 1.2);
x3c3 = [3.4:0.1:4.6];
m3c3 = RAc3 * x3c3 - 25 * (x3c3 - 1.2) + 25 * (x3c3 -3.4);
xc3 = [x1c3,x2c3,x3c3];
mc3 = [m1c3,m2c3,m3c3]; %moment for case_3
subplot(2,2,3)
plot(xc3,mc3)
10 | P a g e

grid on;
xlabel('length of beam in meters')
ylabel('bending moment in kN-m')
title('Load case 3')
%for case_4
load1c4 = 25; %load_1 in kN
load2c4 = 10; %load_2 in kN
load3c4 = -25; %load_3 in kN
load4c4 = 4.6; %load_4 in kN
act1c4 = 1.2; %distance of the load_1 from the left support in m
act2c4 = 1.6; %distance of the load_2 from the left support in m
act3c4 = 3.4; %distance of the load_3 from the left support in m
act4c4 = 3.45; %distance of the load_4 from the left support in m
RBc4 = (load1c4 * act1c4 + load2c4 * act2c4 + load3c4 * act3c4 + load4c4 *
act4c4) / 4.6; %reaction at support-A
RAc4 = 14.6 - RBc4; %reaction at support-B
%To find moments
x1c4 = [0:0.1:1.2];
m1c4 = RAc4 * x1c4;
x2c4 = [1.2:0.1:1.6];
m2c4 = RAc4 * x2c4 - 25 * (x2c4 - 1.2);
x3c4 = [1.6:0.1:3.4];
m3c4 = RAc4 * x3c4 - 25 * (x3c4 - 1.2) - 10 * (x3c4 - 1.6);
x4c4 = [3.4:0.1:3.45];
m4c4 = RAc4 * x4c4 - 25 * (x4c4 - 1.2) - 10 * (x4c4 - 1.6) + 25 *
(x4c4 - 3.4);
x5c4 = [3.45:0.1:4.6];
m5c4 = RAc4 * x5c4 - 25 * (x5c4 - 1.2) - 10 * (x5c4 - 1.6) + 25 *
(x5c4 - 3.4) - 4.6 * (x5c4 - 3.45);
xc4 = [x1c4,x2c4,x3c4,x4c4,x5c4];
mc4 = [m1c4,m2c4,m3c4,m4c4,m5c4]; %moment for case_4
subplot(2,2,4)
plot(xc4,mc4)
grid on;
xlabel('length of beam in meters')
ylabel('bending moment in kN-m')
title('Load case 4')
plot(xc1,mc1,'r-',xc2,mc2,'b:',xc3,mc3,'ko',xc4,mc4,'m*')
grid on;
legend('case-1','case-2','case-3','case-4')
xlabel('length of beam in meters')
ylabel('bending moment in kN-m')
title('Load case 1,2,3, and 4')
11 | P a g e

On-Line Quiz Question
1. i = 8 ; j = 6 ; k = 1 ; l = 2
2. 6.5218 kN (Please refer Page no. 2 for the solution)
3. MX = RA * x – 10 (x – 1.6)
MX=2 = 6.5218 * 2 – 10 (2 – 1.6) = 9.0436 kNm
4. Bending moment (maximum), Mx = RA * (a + R A
2∗w )
Where, ‘a’ is the distance from the left-most support to the point where the uniformly
distributed load starts (in m)
w is the uniformly distributed load (in kN/m)
In this case, w = 1 + k = 1 + 1 = 2 kN/m
Substituting the values in the equation, we get,
Mmax = 1.15 * (2.3 + 1.15
2∗2 ) = 2.9756 kNm
5. The coordinate of ‘x’ where the maximum bending moment occurs is given by:
x = a + R A
w
where, Where, ‘a’ is the distance from the left-most support to the point where the
uniformly distributed load starts (in m)
w is the uniformly distributed load (in kN/m)
Therefore,
x = 2.3 + 1.15
2 = 2.875 m
6. RB = -11.956 kN (Refer the solution in case-3)
7. Let’s imagine a plane at the mid-span of the beam
From Case-3, RB = - 11.956 kN
12 | P a g e

Moments on the right-hand side of the beam: -6.8750 kNm
MATLAB Code for finding the mean:
clear all;
load1 = 25; %load_1 in kN
act1 = 1.2; %distance of the load_1 from the left support in m
load2 = -25; %load_2 in kN
act2 = 3.4;%distance of the load_2 from the left support in m
%support reactions
RB = (load1 * act1 + load2 * act2)/ 4.6; %reaction at support-A
RA = - RB %reaction at support-B
%To find moments
x1 = 0;
for x = 2.3:0.1:3.3
x1 = x1 + 1;
m1(x1) = RA * x - 25 * (x - 1.2);
end
K = sum(m1);
x2 = 0;
for y = 3.4:0.1:4.6
x2 = x2 + 1;
m2(x2) = RA * y - 25 * (y - 1.2) + 25 * (y - 3.4);
end
L = sum(m2);
x = [x1,x2];
m = [m1(x1),m2(x2)];
total = K + L;
Mean = total / (x1+x2)
8. For case_1, maximum bending moment = Load∗a∗b
length of the beam
Where ‘a’ is the distance from the left-most support to the point where the point load
is acting, i.e., a = 1.6
b = length of the beam – a = 4.6 – 1.6 = 3
Maximum bending moment for case_1 = 10∗1.6∗3
4.6 = 10.43 kN-m
For case_2, maximum bending moment = 2.9756 kN-m (refer solution of question 4)
For case_3, maximum bending moment = RA * x
Where, x = 1.2 m and RA = 11.956 kN
Therefore, maximum bending moment for case_3 = 11.956 * 2 = 14.3472 kNm
13 | P a g e

Maximum bending moment = 14.3472 kNm
9. 3
10. Maximum bending moment = RA * x
Maximum bending moment occurs at x = 1.2 m
Maximum bending moment = 23.5536 kNm
11. Minimum bending moment = -7.47 kNm at 1.2 m from the right support.
12. Moment at position x = RA * x – 25 * (x – 1.2) – 10 * (x – 1.6)
At mid-point of the beam, x = 2.3 m
Moment = 19.628 * 2.3 – 25 *(2.3 – 1.2) – 10 * (2.3 – 1.6) = 10.644 kNm
13. The bending moment is ≥ 8 kNm lies in between 0.407566 m to 2.472059 m.
(The MATLAB Code for comparison plots can be helpful here)
14 | P a g e