Statistical Analysis Examples: Understanding Covariance, Hypothesis Testing, Central Tendency, and Probability

In this document we will discuss about Statistical Analysis Examples and below are the summary points of this document:- A negative covariance between years of experience and salary indicates that as experience increases, salary decreases. The correlation between them is also negative. A statistical hypothesis test with a sinus drug showed that there was not enough evidence to prove that the proportion of users who experienced drowsiness was different from 10%. 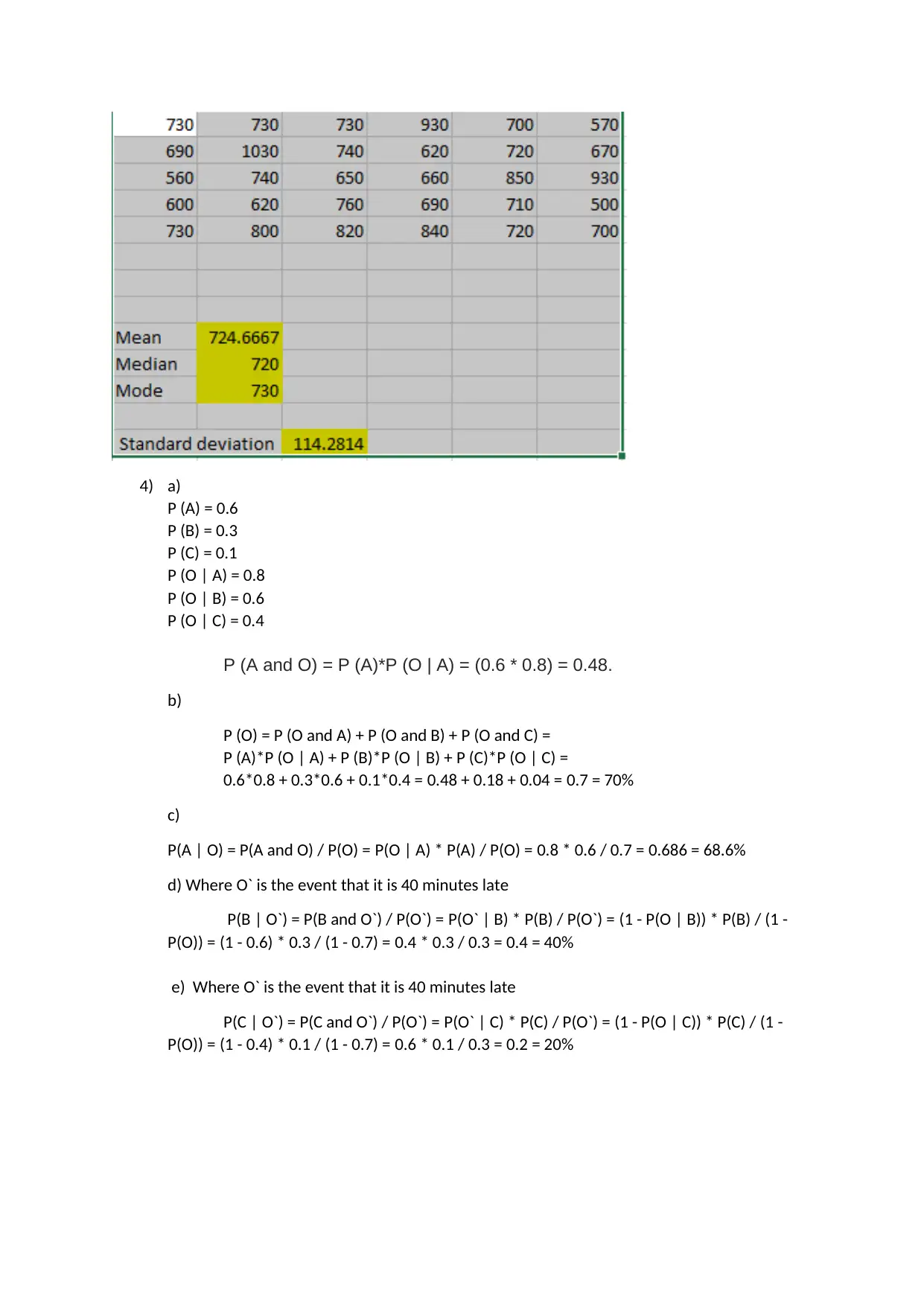In a dataset, the measures of central tendency for a variable were calculated as: mean = 724.6667, median = 720, and mode = 730. The standard deviation was 114.2814, and only one outlier was detected. The empirical rule showed that the data came from a normal distribution. Probabilities were calculated for different events based on given probabilities. For example, the probability of event A given that event O occurred was calculated.

1) a) The covariance between x (number of years of experience) and y (salary) is -12.7143. The
negative covariance indicates that as the number of years of experience increases the salary
decreases.
b) With age the efficiency decreases for which the salary is less and the company must want
that the persons with less number of work experience will give more amount of time in the
company for which their salary is also high.
c) The correlation between x and y is -0.99109. So x and y are negatively correlated i.e. if
once increases then the other decreases.
d) With age the efficiency decreases for which the salary is less and the company must want
that the persons with less number of work experience will give more amount of time in the
company for which their salary is also high.
2) a) Null Hypothesis : 10% of the users of a certain sinus drug experience drowsiness
Alternate hypothesis: 10% of the users of a certain sinus drug does not experience
drowsiness.
b) p = 81/900 = 0.09
So we got the proportion p = 0.09
The test statistics:
z= 0.09−0.1
√ 0.1× 0.9/900
z= −0.01
√0.0001
z=−0.01
0.01
z=−1
At 95% confidence interval the critical value is ±1.96.

So from the above test and critical values we fail to reject null hypothesis so there is not
enough evidence to prove that it is different from 10%.
c) Confidence interval
p ± Z α
2
× √ p(1−p)/n
Here p = 0.09
(1-p) = 0.91, putting the above values in the above expression
0.09 ± 1.96× √ 0.09× 0.91/900
0.09 ± 0.0187
So the confidence interval is (0.0713, 0.1087).
d) Because 0.1 falls between the confidence interval we fail to reject null hypothesis at 5%
significance level.
3) a) The mean is 724.6667.
The median is 720.
The mode is 730.
b) Yes the measures of central tendency agree as Mode > Mean > Median
c) The standard deviation is 114.2814.
d) If we consider mean ± 2 * standard deviation, then the range is
724.6667 ± 2 * 114.2814
(953.2295, 496.1039)
From the interval we can see that only 1 is outlier and its value is 1030.
e) The empirical rule is
68% of data falls within the first standard deviation from the mean.
95% fall within two standard deviations.
99.7% fall within three standard deviations
For 1 standard deviation 724.6667 ± 114.2814 = (838.9481, 610.3853)
Number of observation = 21
Percentage = 70%
For 2 standard deviation = 29
Percentage = 96%
For 3 standard deviation = 724.6667 ±3* 114.2814 = (1067.5112, 381.8225)
Number of observation = 30
Percentage = 100%
So we can say that it comes from Normal population.

4) a)
P (A) = 0.6
P (B) = 0.3
P (C) = 0.1
P (O | A) = 0.8
P (O | B) = 0.6
P (O | C) = 0.4
P (A and O) = P (A)*P (O | A) = (0.6 * 0.8) = 0.48.
b)
P (O) = P (O and A) + P (O and B) + P (O and C) =
P (A)*P (O | A) + P (B)*P (O | B) + P (C)*P (O | C) =
0.6*0.8 + 0.3*0.6 + 0.1*0.4 = 0.48 + 0.18 + 0.04 = 0.7 = 70%
c)
P(A | O) = P(A and O) / P(O) = P(O | A) * P(A) / P(O) = 0.8 * 0.6 / 0.7 = 0.686 = 68.6%
d) Where O` is the event that it is 40 minutes late
P(B | O`) = P(B and O`) / P(O`) = P(O` | B) * P(B) / P(O`) = (1 - P(O | B)) * P(B) / (1 -
P(O)) = (1 - 0.6) * 0.3 / (1 - 0.7) = 0.4 * 0.3 / 0.3 = 0.4 = 40%
e) Where O` is the event that it is 40 minutes late
P(C | O`) = P(C and O`) / P(O`) = P(O` | C) * P(C) / P(O`) = (1 - P(O | C)) * P(C) / (1 -
P(O)) = (1 - 0.4) * 0.1 / (1 - 0.7) = 0.6 * 0.1 / 0.3 = 0.2 = 20%