Research in Finance: Correlation among R&D spending, CEO ownership and Board independence

This project evaluates the correlation among the company’s R&D spending, CEO ownership and Board independence. The Pooled regression is used to test the hypothesis. The results show that CEO ownership has a positive impact on R&D and Board independence does not have any negative impact on R&D.

University
* Semester
RESEARCH IN FINANCE
Student ID:
Student Name:
Submission Date:

Table of Contents
Introduction.......................................................................................................................................1
Regression Equation..........................................................................................................................1
Hypothesis.........................................................................................................................................1
Research Method...............................................................................................................................2
Analysis and Results.........................................................................................................................2
1. Descriptive Statistics..............................................................................................................2
2. Correlation Matrix..................................................................................................................3
3. Covariance Matrix..................................................................................................................3
4. Scatter Plots............................................................................................................................4
Pooled Regression Empirical Results................................................................................................6
1. Interpretation..........................................................................................................................6
2. Normality Test.......................................................................................................................7
3. Fixed Effect Redundancy Test...............................................................................................7
4. Random Effects - Hausman Test............................................................................................8
Conclusion.......................................................................................................................................10
Limitations.......................................................................................................................................11
References.......................................................................................................................................12

Introduction
The main objective of this project is to contact the empirical research to evaluate the
correlation among the company’s R&D spending, when it comes with CEO ownership and
the Board independence. To complete the empirical research it is required to check whether
the CEO ownership or Board independence has any impact on R&D or not. This research
hypothesis will be tested by using the Pooled regression, and it will be run by using the
ordinary least squares regression method, in E – Views statistical tool.
Regression Equation
This section utilizes the Regression analysis, when the independent and dependant
variables are systematically linked with the help of the below mentioned linear equation,
Where,
In the provided case, the equation will be written as follows:
Hypothesis
Based on the Relationship of ownership and RD, the Hypotheses are listed below.
 Null Hypothesis
H0: CEO ownership shows positive impacts on the R&D.
 Alternative Hypothesis
H1: CEO ownership does not show positive impacts on the R&D.
Based on Board independence’s impact on R&D, the hypotheses are listed below.
 Null Hypothesis
H0: The Board of independence shows negative impacts on the R&D.
1

 Alternative Hypothesis
H1: The Board of independence shows no negative impacts on the
R&D.
Research Method
In this research, the three models namely, Fixed effect model, Pooled Regression and
Random effect model are considered for selecting an appropriate research method. The
representation of pooled regression is the difference of what displays via time and also the
dimensions’ variance. It estimates the user model by using the least squares with the
correlation for random and the fixed effect in period dimensions and cross-section
dimensions, robust standing error, GLS weighting, AR error and reordering the data. The
fixed and random effects are used to assume the effects on the estimated weights (Mickey,
Dunn and Clark, 2010).
Analysis and Results
1. Descriptive Statistics
The following table is used to display the descriptive statistics' information about
Board independence, board size, RD, risk, profitability, leverage, MTBR, firm size and
ownership, as represented below (Griffiths, Hill and Lim, 2012).
2

In descriptive statistics, the Mean, kurtosis, Maximum, minimum, Median, standard
deviation, skewness, probability, sum, observation, and the Jarque bera are calculated. The
skewness is used to understand the degree to which the distribution is symmetric, where in
the above table the Board independence is negatively skewed and the other variables like RD
and Ownership are positively skewed when compared to the other three variables. The
kurtosis is used to measures the thickness of the tails (it must have 3 tails). Additionally, the
Board independence contains 0.0024 tail values. The RD and Ownership have high tail
values. Thus, it has a negative kurtosis value.
2. Correlation Matrix
Here, the correlation between the RD with the Board independence, and the RD with
ownership are calculated. The RD with the Board independence is 0.195308, which is
positively correlated, whereas the RD with the ownership is -0.146708, which is negatively
correlated. It is represented in the below figure.
3. Covariance Matrix
Here, the covariance between the RD the Board independence, and the RD with
ownership are calculated. The RD with the Board independence is 5.602589, which are
3

positively correlated, whereas the RD with ownership is -0.092485, which is negatively
correlated. It is represented in the below figure.
4. Scatter Plots
The below scatter plot is used to display the relationship of RD versus ownership.
This plot indicates that the ownership decreases as the RD increases. Thus, it provides a
linear negative relationship between RD and ownership.
4

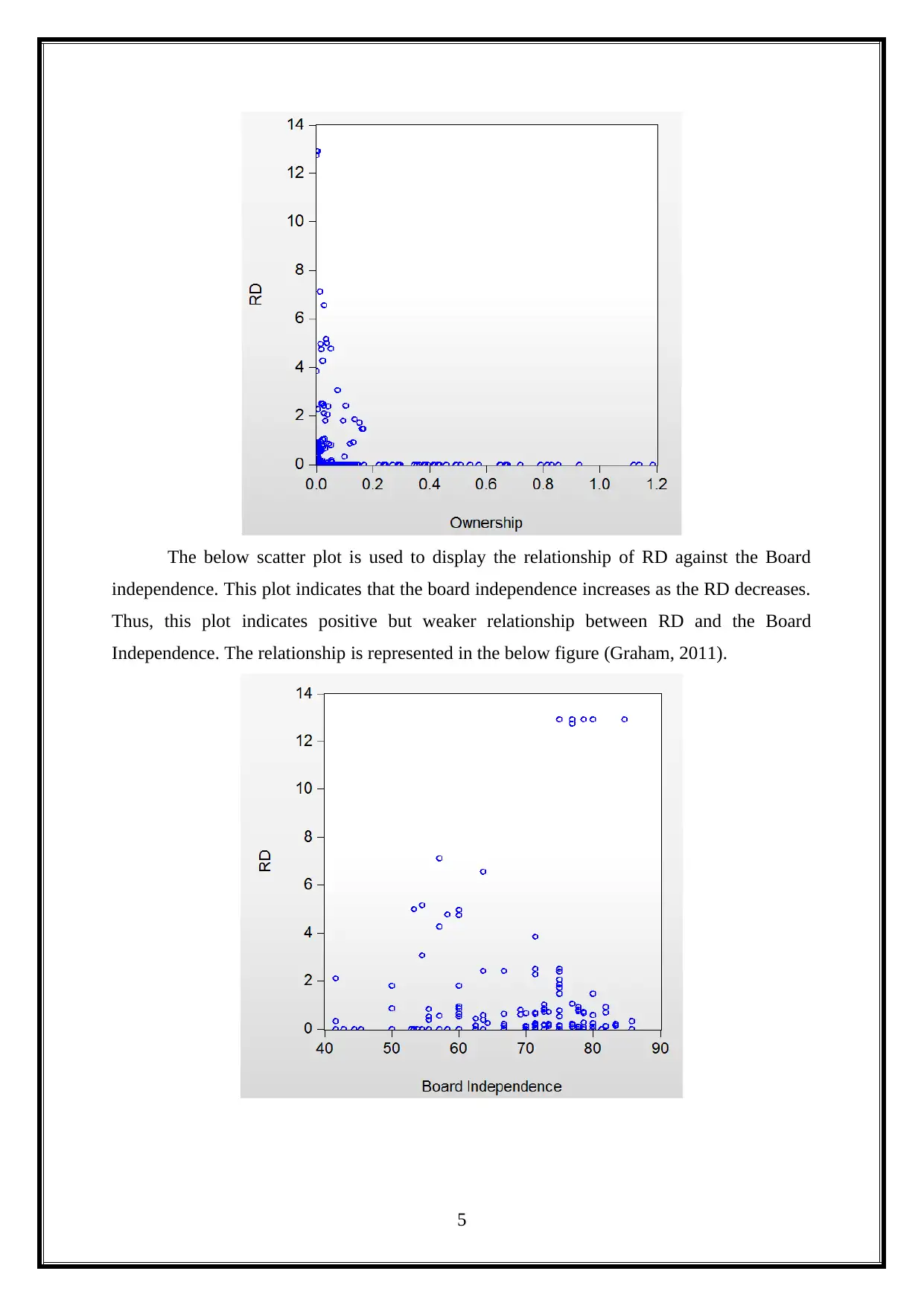
The below scatter plot is used to display the relationship of RD against the Board
independence. This plot indicates that the board independence increases as the RD decreases.
Thus, this plot indicates positive but weaker relationship between RD and the Board
Independence. The relationship is represented in the below figure (Graham, 2011).
5

Pooled Regression Empirical Results
The below table is used to display the Pooled Regression Estimation values, as
represented in the below figure.
1. Interpretation
The pooled regression is calculated as the coefficient values based on dependent
variables like RD. Board independence has a coefficient value of 2.56. The ownership has the
coefficient value of -4.00. Based on the regression, RD with Board independence and RD
with Ownership have 90% level under the pooled regression. Board independence's value has
a positive value, thus it has no negative impact on RD. Therefore, the alternative hypothesis
is rejected. The value of ownership has negative values, thus it has no positive impact on RD.
Therefore, the null hypothesis is also rejected.
To validate the overall significance, it is utilized for displaying the relationship among
the independent and dependent variables. Based on models, it is statistically significant at 99
%. Finally, the null hypothesis on RD with ownership and an alternative hypothesis on Rd
with board independence are rejected, but for proving the best, the below listed tests must be
done (Evans and Basu, 2013).
6

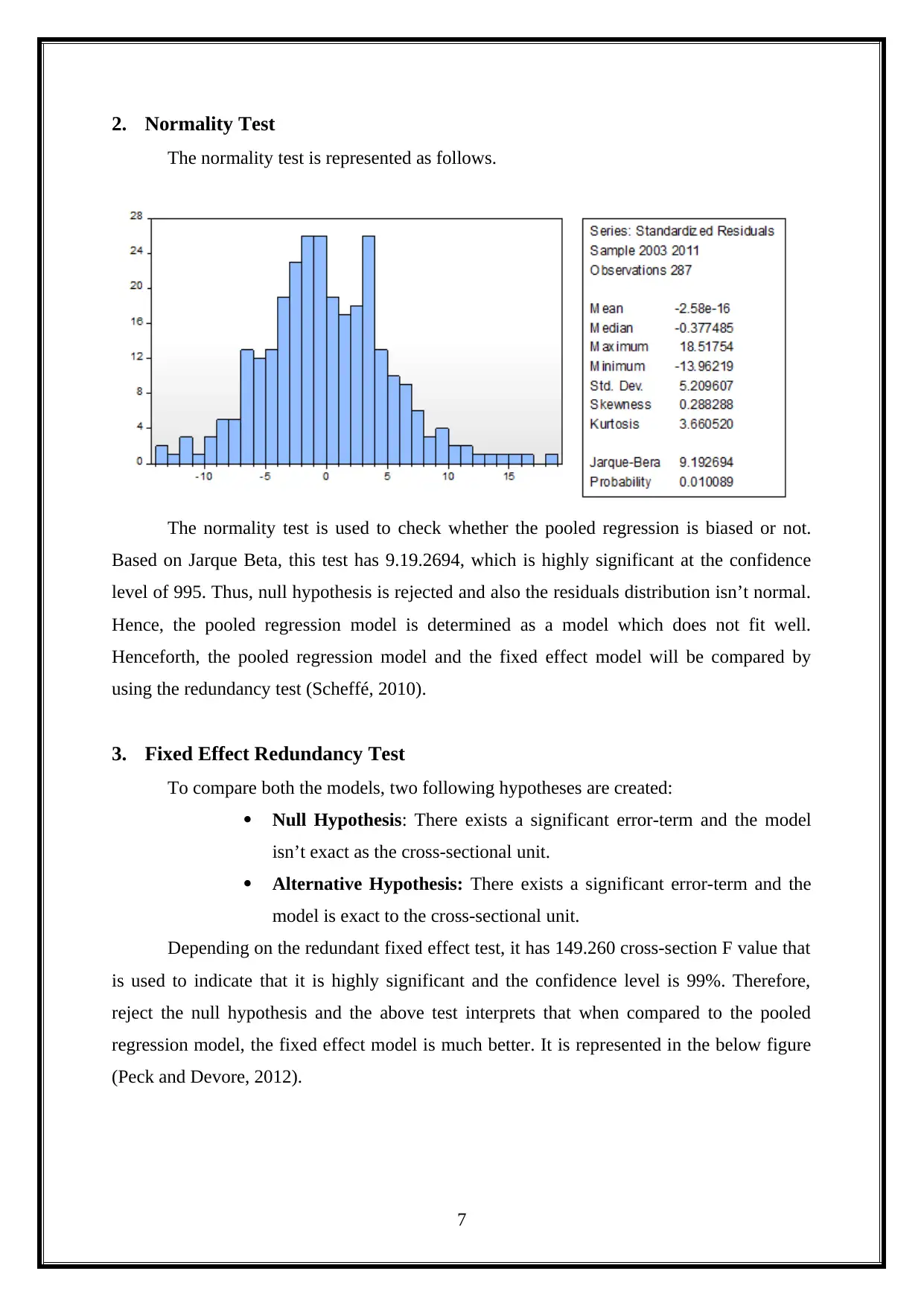
2. Normality Test
The normality test is represented as follows.
The normality test is used to check whether the pooled regression is biased or not.
Based on Jarque Beta, this test has 9.19.2694, which is highly significant at the confidence
level of 995. Thus, null hypothesis is rejected and also the residuals distribution isn’t normal.
Hence, the pooled regression model is determined as a model which does not fit well.
Henceforth, the pooled regression model and the fixed effect model will be compared by
using the redundancy test (Scheffé, 2010).
3. Fixed Effect Redundancy Test
To compare both the models, two following hypotheses are created:
 Null Hypothesis: There exists a significant error-term and the model
isn’t exact as the cross-sectional unit.
 Alternative Hypothesis: There exists a significant error-term and the
model is exact to the cross-sectional unit.
Depending on the redundant fixed effect test, it has 149.260 cross-section F value that
is used to indicate that it is highly significant and the confidence level is 99%. Therefore,
reject the null hypothesis and the above test interprets that when compared to the pooled
regression model, the fixed effect model is much better. It is represented in the below figure
(Peck and Devore, 2012).
7

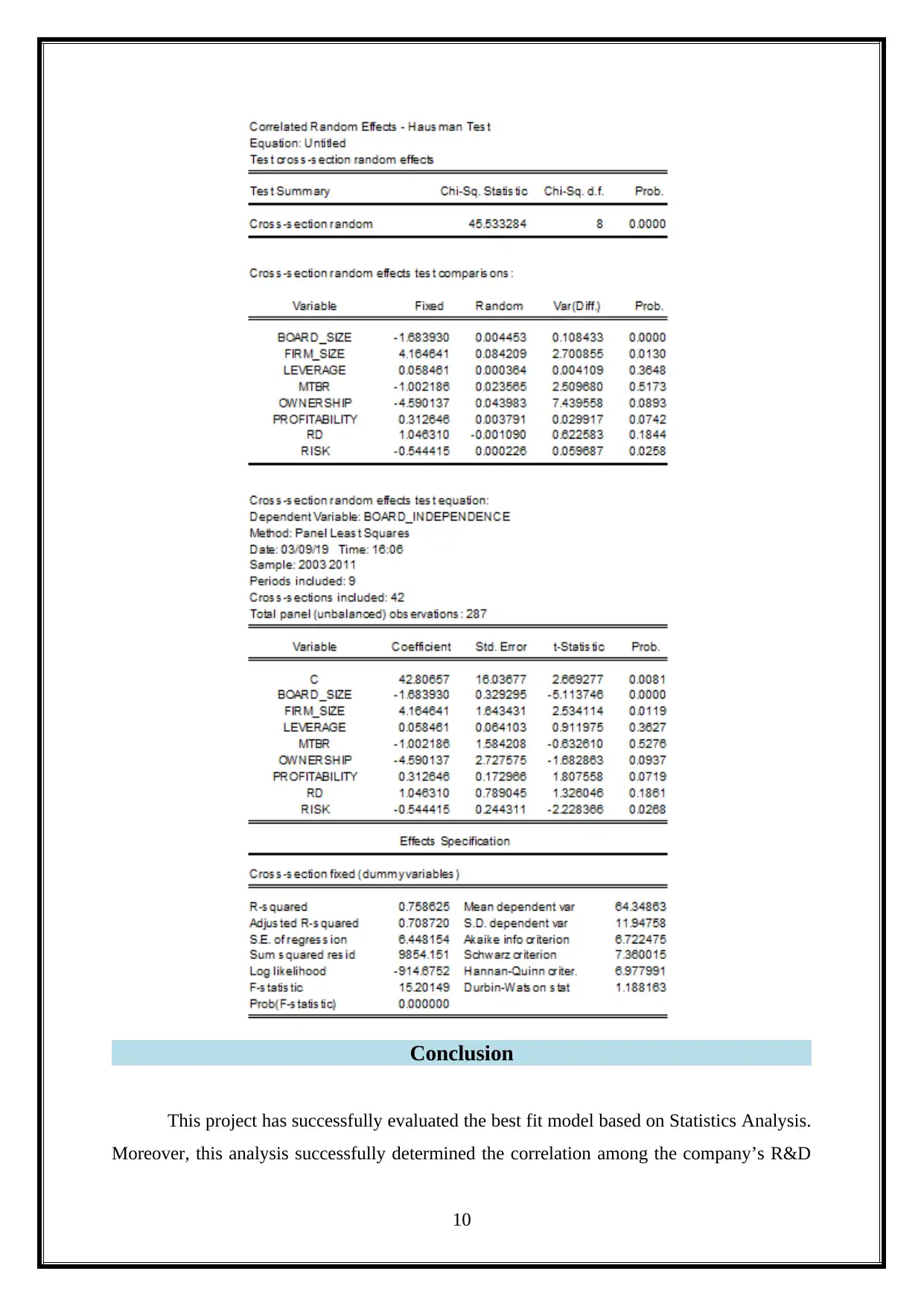
4. Random Effects - Hausman Test
To compare both the models, two following hypotheses are created:
 Null Hypothesis
The significant random effect model is more appropriate.
 Alternative Hypothesis
8

The significant random effect model isn’t appropriate.
Based on the random effect i.e., Hausman test, it has cross-section F value as 45.533,
which is highly significant at the confidence level of 99%. Hence, the null hypothesis cannot
be rejected. Thus, when compared to the other mode, the random effect model is considered
as a good fit.
9

Conclusion
This project has successfully evaluated the best fit model based on Statistics Analysis.
Moreover, this analysis successfully determined the correlation among the company’s R&D
10

spending, when it comes with the CEO ownership and the Board independence. Based on the
random effect model, the ownership shows positive impacts on the R&D. Hence, the Null
hypothesis is accepted which is, "CEO ownership shows positive impacts on the R&D" and
also that the Board independence doesn’t show any negative impacts on the R&D.
Henceforth, the null hypothesis is rejected which is, "The Board of independence has no
negative impacts on the R&D".
Limitations
 Absence of data reliability.
 Ownership and Board independence variables must be assumed as independent
variables because they cannot estimate its result.
 Due to exposure, an error unit might have been included or excluded.
11

References
Evans, J. and Basu, A. (2013). Statistics, data analysis, and decision modeling. Boston:
Pearson.
Graham, A. (2011). Statistics. London: Hodder Education.
Griffiths, W., Hill, R. and Lim, G. (2012). Using EViews for principles of econometrics.
London: John Wiley & Sons Inc.
Mickey, R., Dunn, O. and Clark, V. (2010). Applied statistics. Hoboken, N.J.: Wiley-
Interscience.
Peck, R. and Devore, J. (2012). Statistics. Boston, MA: Brooks/Cole, Cengage Learning.
Scheffé, H. (2010). The analysis of variance. New York: Wiley-Interscience Publication.
12