IEEE Transactions on Automatic Control: DoS Attack Scheduling Analysis
VerifiedAdded on 2022/11/13
|6
|9729
|245
Report
AI Summary
This paper, accepted for publication in IEEE Transactions on Automatic Control, investigates optimal Denial-of-Service (DoS) attack scheduling in Cyber-Physical Systems (CPS). The research focuses on a scenario where an attacker, constrained by energy, aims to degrade system performance by jamming a wireless channel through which a sensor transmits data to a remote estimator. The authors construct optimal attack schedules designed to maximize the expected average estimation error at the estimator. The study also provides optimal attack schedules when a special intrusion detection system (IDS) is present at the estimator, and further explores schedules when the sensor also has energy constraints. The paper's contributions include the development of optimal DoS attack schedules, the analysis of attack strategies with an IDS, and the examination of scenarios with both sensor and attacker energy limitations. Numerical examples are provided to demonstrate the effectiveness of the proposed optimal attack schedules, contributing valuable insights into CPS security.

0018-9286 (c) 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015 1
Optimal Denial-of-Service Attack Scheduling with
Energy Constraint ∗
Heng Zhang1, Peng Cheng1, Ling Shi2 and Jiming Chen 1
Abstract—Security of Cyber-Physical Systems (CPS) has gained in-
creasing attention in recent years. Most existing works mainly investigate
the system performance given some attacking patterns. In this paper, we
investigate how an attacker should schedule its Denial-of-Service (DoS)
attacks to degrade the system performance. Specifically, we consider the
scenario where a sensor sends its data to a remote estimator through a
wireless channel, while an energy-constrained attacker decides whether
to jam the channel at each sampling time. We construct optimal attack
schedules to maximize the expected average estimation error at the
remote estimator. We also provide the optimal attack schedules when
a special intrusion detection system (IDS) at the estimator is given.
We further discuss the optimal attack schedules when the sensor has
energy constraint. Numerical examples are presented to demonstrate the
effectiveness of the proposed optimal attack schedules.
Index Terms—State estimation, DoS attack, energy constraint.
I. INTRODUCTION
Recently, Cyber-Physical Systems (CPS), in which information and
physical elements are closely integrated, have gained much research
interest from various aspects [3]–[5]. Applications of CPS have
a wide spectrum, such as battle field, smart grid, smart building,
intelligent transportation, etc. CPS are vulnerable to different types
of malicious attacks which make the security a fundamental issue for
reliable services [3]. A famous example is that in June 2010 a cyber
worm named ‘stuxnet’ attacked an Iranian nuclear facility at Natanz,
which resulted in 60% hosts damaged [6].
Researchers have investigated security issues in CPS from different
perspectives recently [7], [8]. Teixeira et al. [8] summarized the
characteristics of network attacks and defined an attack space with the
adversary’s priori knowledge of the system model, its disclosure, and
disruption resources. Typical attacks can be categorized into Denial-
of-Service (DoS) attack , replay data attack , and false data injection
attack [8]. DoS attack that blocks the communication between the
system components has been well studied, since it is the most
reachable attack pattern in the attack space [9]. Besides the theoretical
research on DoS attack, some experiments were also conducted to
demonstrate the effect of DoS attacks [10].
In practice, energy constraint is a natural concern for various types
of attackers, which will affect their attack policies [11]–[13]. Law et
al. [11] pointed out that jammers may run out of energy very fast
when their energy budget is limited. Kavitha et al. [12] introduced a
random DoS attacker who randomly decides to jam the channel or
sleep in order to save the energy.
Most existing works mainly investigate the system performance
for given attack patterns. The study of the adversary’s optimal attack
1H. Zhang, P. Cheng and J. Chen are with State Key Labora-
tory of Industrial Control Technology, Zhejiang University, Hangzhou,
China ezhangheng@gmail.com, pcheng@iipc.zju.edu.cn,
jmchen@iipc.zju.edu.cn
2L. Shi is with the Department of Electronic and Computer Engineering,
Hong Kong University of Science and Technology, Hong Kong, China
eesling@ust.hk
∗The work was partially supported by NSFC under grant U1401253, and
National Program for Special Support of Top-Notch Young Professionals,
Fundamental Research Funds for the Central Universities 2014XZZX003-
25, NCET-11-0445. The work by L. Shi was supported by an HKUST
Caltech Partnership FP004. Part of this work has been presented by IEEE
CDC 2013 [1]. [2] provides a complete proof of all results in this work..
(Corresponding author: Jiming Chen.)
schedules and the corresponding consequences is an important aspect
in CPS security as pointed out in [14]. Motivated by this, we aim
to answer how to optimally schedule the attack so as to maximize
the attacking effect on a CPS. Specifically, we consider a system
where one sensor processes the measurements and sends the data
to a remote estimator through a wireless channel. An attacker has a
limited attacking energy budget, and decides at each sampling time
whether or not to jam the channel in order to degrade the remote
estimation quality. To the best of our knowledge, this is the first
work on the DoS attack schedules against remote state estimation.
The main contributions of this paper are summarized as follows:
1) We construct the optimal DoS attack schedules, which maxi-
mize the expected average estimation error.
2) We present the optimal attack schedules when a special IDS in
the estimator is given.
3) We further present the optimal attack schedules when both the
sensor and the attacker have energy constraints.
The remainder of the paper is organized as follows: In Section
II, we formulate the attack schedule problems. In Section III, we
construct the optimal DoS attack schedules for maximizing the
expected average estimation error. In Section IV, we present the
optimal attack schedules for avoiding a given intrusion detection
system. In Section V, we study the optimal attack schedules when the
sensor also has energy constraint. In Section VI, numerical examples
are shown to illustrate the results. Finally, Section VII concludes the
paper.
Notations: Sn
+ stands for the set of n × n positive semi-definite
matrices. Z+ stands for the set of positive integers. E[X] is the mean
of random variable X , and E[X|Y ] is the mean of random variable
X conditioned on Y , respectively. k γ k0 is used to denote the zero
norm of γ, which is the number of nonzero entries of the vector γ.
T r(·) represents the trace of matrix.
II. PROBLEM FORMULATION AND PRELIMINARIES
A. Problem formulation
Consider the following system (Fig. 1)
xk+1 = Axk + wk ,
yk = Cxk + vk , (1)
where xk ∈ Rn x is the system state with nx ∈ Z+ , yk ∈ Rn y is
the sensor measurement with ny ∈ Z+ , wk ∈ Rn x is the process
noise, vk ∈ R n y is the measurement noise, and wk and vk are
uncorrelated zero mean Gaussian noises with covariance Σ w and
Σv , respectively. The pair (A, C) is assumed to be observable and
(A, Σ 1
2
w ) is controllable.
Fig. 1. Schematic of attack on the network.
After yk is obtained, the sensor pre-estimates the state xk , and
then sends its minimum mean squared error (MMSE) estimate ˆxs
k =
E[xk |y1, . . . , yk ] to a remote estimator through a wireless channel.
We consider the scenario that there is an attacker which degrades
the remote estimation quality by jamming the wireless channel. The
attacker has a limited energy budget and has to determine whether to
jam the channel or not at each sampling time. It is assumed that the
packet will arrive at the remote estimator if there is no DoS attack
during the transmission.
0000–0000/00$00.00 c 2015 IEEE
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015 1
Optimal Denial-of-Service Attack Scheduling with
Energy Constraint ∗
Heng Zhang1, Peng Cheng1, Ling Shi2 and Jiming Chen 1
Abstract—Security of Cyber-Physical Systems (CPS) has gained in-
creasing attention in recent years. Most existing works mainly investigate
the system performance given some attacking patterns. In this paper, we
investigate how an attacker should schedule its Denial-of-Service (DoS)
attacks to degrade the system performance. Specifically, we consider the
scenario where a sensor sends its data to a remote estimator through a
wireless channel, while an energy-constrained attacker decides whether
to jam the channel at each sampling time. We construct optimal attack
schedules to maximize the expected average estimation error at the
remote estimator. We also provide the optimal attack schedules when
a special intrusion detection system (IDS) at the estimator is given.
We further discuss the optimal attack schedules when the sensor has
energy constraint. Numerical examples are presented to demonstrate the
effectiveness of the proposed optimal attack schedules.
Index Terms—State estimation, DoS attack, energy constraint.
I. INTRODUCTION
Recently, Cyber-Physical Systems (CPS), in which information and
physical elements are closely integrated, have gained much research
interest from various aspects [3]–[5]. Applications of CPS have
a wide spectrum, such as battle field, smart grid, smart building,
intelligent transportation, etc. CPS are vulnerable to different types
of malicious attacks which make the security a fundamental issue for
reliable services [3]. A famous example is that in June 2010 a cyber
worm named ‘stuxnet’ attacked an Iranian nuclear facility at Natanz,
which resulted in 60% hosts damaged [6].
Researchers have investigated security issues in CPS from different
perspectives recently [7], [8]. Teixeira et al. [8] summarized the
characteristics of network attacks and defined an attack space with the
adversary’s priori knowledge of the system model, its disclosure, and
disruption resources. Typical attacks can be categorized into Denial-
of-Service (DoS) attack , replay data attack , and false data injection
attack [8]. DoS attack that blocks the communication between the
system components has been well studied, since it is the most
reachable attack pattern in the attack space [9]. Besides the theoretical
research on DoS attack, some experiments were also conducted to
demonstrate the effect of DoS attacks [10].
In practice, energy constraint is a natural concern for various types
of attackers, which will affect their attack policies [11]–[13]. Law et
al. [11] pointed out that jammers may run out of energy very fast
when their energy budget is limited. Kavitha et al. [12] introduced a
random DoS attacker who randomly decides to jam the channel or
sleep in order to save the energy.
Most existing works mainly investigate the system performance
for given attack patterns. The study of the adversary’s optimal attack
1H. Zhang, P. Cheng and J. Chen are with State Key Labora-
tory of Industrial Control Technology, Zhejiang University, Hangzhou,
China ezhangheng@gmail.com, pcheng@iipc.zju.edu.cn,
jmchen@iipc.zju.edu.cn
2L. Shi is with the Department of Electronic and Computer Engineering,
Hong Kong University of Science and Technology, Hong Kong, China
eesling@ust.hk
∗The work was partially supported by NSFC under grant U1401253, and
National Program for Special Support of Top-Notch Young Professionals,
Fundamental Research Funds for the Central Universities 2014XZZX003-
25, NCET-11-0445. The work by L. Shi was supported by an HKUST
Caltech Partnership FP004. Part of this work has been presented by IEEE
CDC 2013 [1]. [2] provides a complete proof of all results in this work..
(Corresponding author: Jiming Chen.)
schedules and the corresponding consequences is an important aspect
in CPS security as pointed out in [14]. Motivated by this, we aim
to answer how to optimally schedule the attack so as to maximize
the attacking effect on a CPS. Specifically, we consider a system
where one sensor processes the measurements and sends the data
to a remote estimator through a wireless channel. An attacker has a
limited attacking energy budget, and decides at each sampling time
whether or not to jam the channel in order to degrade the remote
estimation quality. To the best of our knowledge, this is the first
work on the DoS attack schedules against remote state estimation.
The main contributions of this paper are summarized as follows:
1) We construct the optimal DoS attack schedules, which maxi-
mize the expected average estimation error.
2) We present the optimal attack schedules when a special IDS in
the estimator is given.
3) We further present the optimal attack schedules when both the
sensor and the attacker have energy constraints.
The remainder of the paper is organized as follows: In Section
II, we formulate the attack schedule problems. In Section III, we
construct the optimal DoS attack schedules for maximizing the
expected average estimation error. In Section IV, we present the
optimal attack schedules for avoiding a given intrusion detection
system. In Section V, we study the optimal attack schedules when the
sensor also has energy constraint. In Section VI, numerical examples
are shown to illustrate the results. Finally, Section VII concludes the
paper.
Notations: Sn
+ stands for the set of n × n positive semi-definite
matrices. Z+ stands for the set of positive integers. E[X] is the mean
of random variable X , and E[X|Y ] is the mean of random variable
X conditioned on Y , respectively. k γ k0 is used to denote the zero
norm of γ, which is the number of nonzero entries of the vector γ.
T r(·) represents the trace of matrix.
II. PROBLEM FORMULATION AND PRELIMINARIES
A. Problem formulation
Consider the following system (Fig. 1)
xk+1 = Axk + wk ,
yk = Cxk + vk , (1)
where xk ∈ Rn x is the system state with nx ∈ Z+ , yk ∈ Rn y is
the sensor measurement with ny ∈ Z+ , wk ∈ Rn x is the process
noise, vk ∈ R n y is the measurement noise, and wk and vk are
uncorrelated zero mean Gaussian noises with covariance Σ w and
Σv , respectively. The pair (A, C) is assumed to be observable and
(A, Σ 1
2
w ) is controllable.
Fig. 1. Schematic of attack on the network.
After yk is obtained, the sensor pre-estimates the state xk , and
then sends its minimum mean squared error (MMSE) estimate ˆxs
k =
E[xk |y1, . . . , yk ] to a remote estimator through a wireless channel.
We consider the scenario that there is an attacker which degrades
the remote estimation quality by jamming the wireless channel. The
attacker has a limited energy budget and has to determine whether to
jam the channel or not at each sampling time. It is assumed that the
packet will arrive at the remote estimator if there is no DoS attack
during the transmission.
0000–0000/00$00.00 c 2015 IEEE
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

0018-9286 (c) 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
2 IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015
Denote γk = 1 or 0 as the attacker’s decision variable at time k,
and γ as a schedule that defines γk at each k. When the attacker
launches an attack and jams the channel, the sensor data packet will
be dropped with probability α. Denote θk = 1 or 0 as the indicator
function whether the data packet drops or not. We assume that θk ’s
are i.i.d. Bernoulli random variables with E(θk ) = α 1.
Denote all the data packet received at the estimator until time k
as D(γ1:k ). The remote estimator then computes its own MMSE
estimate ˆxk and its corresponding estimation error covariance Pk
based on D(γ1:k ), e.g., ˆxk (γ1:k ) = E[xk |D(γ1:k )] and Pk (γ1:k ) =
E[(xk − ˆxk )(xk − ˆxk )′ |D(γ1:k )]. For simplicity, we write ˆxk (γ1:k )
as ˆxk , etc., when the schedule γ1:k is given.
Consider a finite horizon T . Due to the finite energy constraint,
assume the attacker can only launch n attacks from k = 1to k = T,
i.e., k γ k0= n.
Average Error: For a given attack schedule γ, define J a (γ) as
the average expected estimation error covariance matrix, i.e.,
J a (γ) = 1
T
TX
k=1
E[Pk (γk )].
In this paper, we aim to solve the following problem in the
viewpoint of the attacker:
Problem 2.1:
max
γ∈Γ T r[Ja (γ)],
s.t. k γ k0= n,
where Γ = {0, 1}T is the set of all possible attack schedules.
III. OPTIMAL ATTACK SCHEDULE ANALYSIS
A. State estimation under DoS attack
In this section, we present some properties of the estimation error
at the remote estimator under a DoS attack.
The MMSE estimate ˆxs
k is obtained from a standard Kalman filter.
Let P s
k be the estimation error covariance matrix of ˆxs
k . Standard
Kalman filtering analysis shows thatP s
k converges exponentially to its
steady-state value P . 2 For brevity, we assumeΠ0 = P , then it can be
easily obtained that P s
k = P for all k ∈ [1, T ]. Define h, hk : Sn x
+ →
Sn x
+ as h(X) , AXA ′ + Σw , and hk (X) , h ◦ h ◦ · · · ◦ h| {z }
k times
(X) .
From [17], the following result holds.
Lemma 3.1: The function h has following property:
P ≤ h(P ) ≤ h2(P ) ≤ · · · ≤ hk (P ) ≤ · · · , ∀k ∈ Z+ .
It is straightforward to show that at the remote estimator, ˆxk and
Pk are obtained as follows [18]:
(ˆxk , Pk ) = (Aˆxk−1 , h(Pk−1 )), if γk = 1 and θk = 1,
(ˆxs
k , P ), otherwise.
Assume the data packet is delivered to the remote estimator
successfully at time s, and the attacker launches m consecutive
attacks from time s + 1 to s + m. The state space of the error
covariance matrix Pk in this period is {P , h(P ), . . . , hm (P )}.
1Since the bit error rate (BER) is fixed in every attack time when the
attacker exploits the same energy to jam the channel [15], we assume that the
rate of successful attacks follows a Bernoulli probability distribution.
2Since the pair (A, C) is observable and (A, Σ 1
2
w ) is controllable, P
uniquely exists and can be obtained from the discrete algebraic Riccati
equation. Even if the assumption on controllability and observability fails,
there are other iterative algorithms that can ensure quick convergence to
the stabilizing solution for the steady-state Kalman filtering [16]. Thus it is
reasonable to assume that Π0 = P .
We can see that the error covariance matrix Pk during the consec-
utive attack period [s + 1, s + m]is a stationary Markov chain, and
the transition probability matrix (pij ) is given by
pij = P r{Pk = hj (P )|Pk−1 = hi (P )} =
α, j = i + 1,
1 − α, j = 0,
0, others,
(2)
i, j = 0, 1, 2, . . . , m.Moreover, we have the following properties for
Pk , k ∈ [s + 1, s + m].
Property 3.1: During the consecutive attack period [s + 1, s + m]:
1) the distribution of the error covariance matrix Ps+k can be
computed as
P r{Ps+k = hi (P )} = αi − αi+1 , i = 0, 1, . . . , k − 1;
αk , i = k.
2) the conditional probability can be computed as follows:
P r{Ps+k = hj (P )|Ps = hi (P )} = αj − αj+1 , j = 0, . . . , k − 1;
αk , j = i + k.
This property can be easily obtained from (2) by mathematical
induction method. Due to the space limitation, the proof is omitted.
Property 3.2: 1) If the packet is not received at the remote estimator
at time s, then E[Ps+m |Ps ≥ P ] ≥ E[Ps+m |Ps = P ].
2) Consider two different consecutive attacking periods, n1 and
n2, where n1 ≥ n2. Then E[Ps+n 1 ] ≥ E[Ps+n 2 ].
An attack scheme with given attacking number n can be divided
into the following consecutive attacking sequences, k1, k2, . . . , ks ,
i.e.,
(0, · · · , 0,1, · · · , 1
| {z }
k1 times
, 0, · · · , 0,1, · · · , 1
| {z }
k2 times
, 0, · · · , 0,1, · · · , 1
| {z }
ks times
, 0, · · · , 0),
where P s
i=1 ki = n . Note that each neighboring sequences are
divided by at least one zero. Using Property 3.1, we have
J a (γ) = 1
T
TX
k=1
E[Pk (γk )] = 1
T
sX
i=1
kiX
n i =1
E[Psi +n i ] + T − n
T P
= 1
T
sX
i=1
kiX
n i =1
[
n i −1
X
m=0
hm (P )(αm − αm+1 ) + αn i hn i (P )]
+T − n
T P . (3)
Note that (3) is independent of the attack start sequence si , i =
1, 2, . . . , s, which means that any permutation of the ki ’s will lead
to the same average expected estimation error. Thus, for the con-
secutive attack sequences k1, k2, . . . , ks , we define γk1 ⊕k 2 ⊕···⊕k s
1:T
as the set of attack schedules which have the same perfor-
mance J (k 1 ⊕k 2 ⊕···⊕k s )
a,1:T . For simplicity, we write γk1 ⊕k 2 ⊕···⊕k s
1:T as
γk1 ⊕k 2 ⊕···⊕k s , and write J (k 1 ⊕k 2 ⊕···⊕k s )
a,1:T as J (k 1 ⊕k 2 ⊕···⊕k s )
a , when
the time horizon [1, T ]is given. In particular, let γn be the set of
attack schedules with a consecutive attack sequence n, which have
the same performance J (n)
a .
Property 3.3: The following statements are true.
1) J (n 1 )
a ≤ J (n 2 )
a , where n1 ≤ n2.
2) J (n 1 ⊕n 2 )
a ≤ J (n)
a , where n = n1 + n2.
3) J (n 1 ⊕n 2 ⊕···⊕n s )
a ≤ J (n)
a , where n = n1 + n2 + · · · + ns .
4) J (m 1 ⊕m 2 )
a ≤ J (n 1 ⊕n 2 )
a , where m1 + m2 = n 1 + n2 and
max{m1, m2, n1, n2} is n1 or n2.
Proof: See the Appendix.
From statement 1) and 4) in Property 3.3, we can see that the
more the attack times are grouped together, the lager the system cost
becomes. Statement 2) and 3) demonstrate that consecutive attack is
much better than scattered attack from the viewpoint of attacker.
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
2 IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015
Denote γk = 1 or 0 as the attacker’s decision variable at time k,
and γ as a schedule that defines γk at each k. When the attacker
launches an attack and jams the channel, the sensor data packet will
be dropped with probability α. Denote θk = 1 or 0 as the indicator
function whether the data packet drops or not. We assume that θk ’s
are i.i.d. Bernoulli random variables with E(θk ) = α 1.
Denote all the data packet received at the estimator until time k
as D(γ1:k ). The remote estimator then computes its own MMSE
estimate ˆxk and its corresponding estimation error covariance Pk
based on D(γ1:k ), e.g., ˆxk (γ1:k ) = E[xk |D(γ1:k )] and Pk (γ1:k ) =
E[(xk − ˆxk )(xk − ˆxk )′ |D(γ1:k )]. For simplicity, we write ˆxk (γ1:k )
as ˆxk , etc., when the schedule γ1:k is given.
Consider a finite horizon T . Due to the finite energy constraint,
assume the attacker can only launch n attacks from k = 1to k = T,
i.e., k γ k0= n.
Average Error: For a given attack schedule γ, define J a (γ) as
the average expected estimation error covariance matrix, i.e.,
J a (γ) = 1
T
TX
k=1
E[Pk (γk )].
In this paper, we aim to solve the following problem in the
viewpoint of the attacker:
Problem 2.1:
max
γ∈Γ T r[Ja (γ)],
s.t. k γ k0= n,
where Γ = {0, 1}T is the set of all possible attack schedules.
III. OPTIMAL ATTACK SCHEDULE ANALYSIS
A. State estimation under DoS attack
In this section, we present some properties of the estimation error
at the remote estimator under a DoS attack.
The MMSE estimate ˆxs
k is obtained from a standard Kalman filter.
Let P s
k be the estimation error covariance matrix of ˆxs
k . Standard
Kalman filtering analysis shows thatP s
k converges exponentially to its
steady-state value P . 2 For brevity, we assumeΠ0 = P , then it can be
easily obtained that P s
k = P for all k ∈ [1, T ]. Define h, hk : Sn x
+ →
Sn x
+ as h(X) , AXA ′ + Σw , and hk (X) , h ◦ h ◦ · · · ◦ h| {z }
k times
(X) .
From [17], the following result holds.
Lemma 3.1: The function h has following property:
P ≤ h(P ) ≤ h2(P ) ≤ · · · ≤ hk (P ) ≤ · · · , ∀k ∈ Z+ .
It is straightforward to show that at the remote estimator, ˆxk and
Pk are obtained as follows [18]:
(ˆxk , Pk ) = (Aˆxk−1 , h(Pk−1 )), if γk = 1 and θk = 1,
(ˆxs
k , P ), otherwise.
Assume the data packet is delivered to the remote estimator
successfully at time s, and the attacker launches m consecutive
attacks from time s + 1 to s + m. The state space of the error
covariance matrix Pk in this period is {P , h(P ), . . . , hm (P )}.
1Since the bit error rate (BER) is fixed in every attack time when the
attacker exploits the same energy to jam the channel [15], we assume that the
rate of successful attacks follows a Bernoulli probability distribution.
2Since the pair (A, C) is observable and (A, Σ 1
2
w ) is controllable, P
uniquely exists and can be obtained from the discrete algebraic Riccati
equation. Even if the assumption on controllability and observability fails,
there are other iterative algorithms that can ensure quick convergence to
the stabilizing solution for the steady-state Kalman filtering [16]. Thus it is
reasonable to assume that Π0 = P .
We can see that the error covariance matrix Pk during the consec-
utive attack period [s + 1, s + m]is a stationary Markov chain, and
the transition probability matrix (pij ) is given by
pij = P r{Pk = hj (P )|Pk−1 = hi (P )} =
α, j = i + 1,
1 − α, j = 0,
0, others,
(2)
i, j = 0, 1, 2, . . . , m.Moreover, we have the following properties for
Pk , k ∈ [s + 1, s + m].
Property 3.1: During the consecutive attack period [s + 1, s + m]:
1) the distribution of the error covariance matrix Ps+k can be
computed as
P r{Ps+k = hi (P )} = αi − αi+1 , i = 0, 1, . . . , k − 1;
αk , i = k.
2) the conditional probability can be computed as follows:
P r{Ps+k = hj (P )|Ps = hi (P )} = αj − αj+1 , j = 0, . . . , k − 1;
αk , j = i + k.
This property can be easily obtained from (2) by mathematical
induction method. Due to the space limitation, the proof is omitted.
Property 3.2: 1) If the packet is not received at the remote estimator
at time s, then E[Ps+m |Ps ≥ P ] ≥ E[Ps+m |Ps = P ].
2) Consider two different consecutive attacking periods, n1 and
n2, where n1 ≥ n2. Then E[Ps+n 1 ] ≥ E[Ps+n 2 ].
An attack scheme with given attacking number n can be divided
into the following consecutive attacking sequences, k1, k2, . . . , ks ,
i.e.,
(0, · · · , 0,1, · · · , 1
| {z }
k1 times
, 0, · · · , 0,1, · · · , 1
| {z }
k2 times
, 0, · · · , 0,1, · · · , 1
| {z }
ks times
, 0, · · · , 0),
where P s
i=1 ki = n . Note that each neighboring sequences are
divided by at least one zero. Using Property 3.1, we have
J a (γ) = 1
T
TX
k=1
E[Pk (γk )] = 1
T
sX
i=1
kiX
n i =1
E[Psi +n i ] + T − n
T P
= 1
T
sX
i=1
kiX
n i =1
[
n i −1
X
m=0
hm (P )(αm − αm+1 ) + αn i hn i (P )]
+T − n
T P . (3)
Note that (3) is independent of the attack start sequence si , i =
1, 2, . . . , s, which means that any permutation of the ki ’s will lead
to the same average expected estimation error. Thus, for the con-
secutive attack sequences k1, k2, . . . , ks , we define γk1 ⊕k 2 ⊕···⊕k s
1:T
as the set of attack schedules which have the same perfor-
mance J (k 1 ⊕k 2 ⊕···⊕k s )
a,1:T . For simplicity, we write γk1 ⊕k 2 ⊕···⊕k s
1:T as
γk1 ⊕k 2 ⊕···⊕k s , and write J (k 1 ⊕k 2 ⊕···⊕k s )
a,1:T as J (k 1 ⊕k 2 ⊕···⊕k s )
a , when
the time horizon [1, T ]is given. In particular, let γn be the set of
attack schedules with a consecutive attack sequence n, which have
the same performance J (n)
a .
Property 3.3: The following statements are true.
1) J (n 1 )
a ≤ J (n 2 )
a , where n1 ≤ n2.
2) J (n 1 ⊕n 2 )
a ≤ J (n)
a , where n = n1 + n2.
3) J (n 1 ⊕n 2 ⊕···⊕n s )
a ≤ J (n)
a , where n = n1 + n2 + · · · + ns .
4) J (m 1 ⊕m 2 )
a ≤ J (n 1 ⊕n 2 )
a , where m1 + m2 = n 1 + n2 and
max{m1, m2, n1, n2} is n1 or n2.
Proof: See the Appendix.
From statement 1) and 4) in Property 3.3, we can see that the
more the attack times are grouped together, the lager the system cost
becomes. Statement 2) and 3) demonstrate that consecutive attack is
much better than scattered attack from the viewpoint of attacker.
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST

0018-9286 (c) 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015 3
B. Optimal attack schedule design
Now we are ready to present the optimal attack schedule for
Problem 2.1.
Theorem 3.1: The optimal attack schedule that solves Problem 2.1
is anyone that belongs to γn , and the corresponding cost is given by
T r(J a )max = 1
T
nX
i=1
T r[hi (α, P )] +T − nα
T T r(P ), (4)
where hi (α, P ) = [(n − i)(αi − αi+1 ) + αi ]hi (P ).
Proof: A direct result from Property 3.3 2) and 3).
As a byproduct, we can obtain the worst attack strategy which
minimizes the expected average error covariance.
Problem 3.1:
min
γ∈Γ T r[Ja (γ)],
s.t. k γ k0= n,
The solution of Problem 3.1 is given by the following theorem.
Theorem 3.2: 1) If n ≤ 1
2 T , an optimal solution for Problem 3.1
is anyone in γ1⊕1⊕···⊕1 , and the corresponding cost is given by
T r(J a )min = T − nα
T T r(P ) +nα
T T r[h(P )]. (5)
2) If n > 1
2 T , an optimal solution for Problem 3.1 is
((1 · · · 1
| {z }
z times
0) · · · (1 · · · 1
| {z }
z times
0)
| {z }
r 1 times
( 1 · · · 1
| {z }
m 1 times
0 1 · · · 1
| {z }
m 2 times
) (0 1 · · · 1
| {z }
z times
) · · · (0 1 · · · 1
| {z }
z times
)
| {z }
r 2 times
),
where r1 +r2 = T −n−1, z = ⌊ n
T−n ⌋,3 and m1 = m2 = m
2 if m is
even, m1 = ⌊ m
2 ⌋, m2 = m−m1 or m1 = ⌊ m
2 ⌋ + 1, m2 = m−m1
if m is odd, with m = z + [n mod (T − n)].4 The resulting cost is
T r(J a )min = 1
T T r{(T − n − 1)
zX
i=1
hi (α, P ) +
m 1X
i=1
hi (α, P )
+
m 2X
i=1
hi (α, P ) + [(T − n) + m(1 − α)
+z(1 − α)(T − n − 1)]P }, (6)
where hi (α, P ) = [(n − i)(αi − αi+1 ) + αi ]hi (P ).
Proof: A direct result from Property 3.3 3) and 4).
From the above two theorems, one can see that grouping the
attacks together leads to maximal attacking effect, while separating
the attacks as uniformly as possible leads to the minimal degradation.
Thus the results can be viewed as the upper and lower bound of the
damage an arbitrary attack schedule can make.
IV. OPTIMAL ATTACK SCHEDULES AGAINST A GIVEN IDS
The aforementioned problems are discussed under the assumption
that the channel is perfect and there is no defensive measure. In
practical applications, when the estimator considers unknown factors
from environment changes or adversary’s intrusion, which may lead
to data drops, a detector is often designed at the receiver side as a
first step to reduce the effectiveness of these factors. For example,
packet reception rate ( PRR ) at the receiver side is proposed as the
criteria for intrusion detection in [19]. PRR is the rate of packets
reception that are successfully delivered to the estimator compared
to the number of packets that have been sent out by the sensor.
3⌊x⌋ is floor function, which is defined as the largest integer that is less
than real number x.
4mod is defined as modulo operation, i.e., n mod m is the remainder in
division n
m , where n and m are two positive integer.
In practice, the PRR can be computed for a given length of a time
window τ, i.e., PRR = σ
τ , where σ is the packet reception numbers
in the time window. If the PRR is too small, the detector will deduce
that there may exist an attacker, which triggers an alarm to alert
the sensor. Then the sensor can use channel hopping technology to
guarantee the packet can be received by the remote estimator [20]. In
this paper, we assume that the alarm is triggered if PRR ≤ PRR 0,
where PRR 0 is a given alarm bound. 5
Fig. 2. Schematic of attack on the network against state estimation with an
intrusion detector.
Before introducing the attack schedule against the IDS mechanism,
we present a property to help formulate the attack optimization
problem.
Property 4.1: The alarm triggering condition PRR ≤ PRR 0 is
equivalent to Pk h d(P ), k = 1, 2, . . . , T, where d = τ − σ0,
σ0 = max{σ|σ
τ ≤ PRR 0}.
Proof: See the Appendix.
Remark 4.1: From Property 4.1, any attack schedule with at most
d times consecutive attack, i.e., P k+τ
i=k+1 γi ≤ d, k = 0, 1, . . . , T −τ,
can guarantee that the attack action will not be detected by the esti-
mator. In fact, time window τ and threshold PRR 0 can be evaluated
by the attacker when he eavesdrops the transmission channels before
taking attack actions.
In order not to be detected by IDS, we consider Problem 2.1 with
an additional constraint, i.e.,
Problem 4.1:
max
γ∈Γ T r[Ja (γ)],
s.t. k γ k0= n,
k+τX
i=k+1
γi ≤ d, k ∈ [0, T − τ ]. (7)
The following result presents the optimal solution to Problem 4.1.
Theorem 4.1: Consider Problem 4.1. Let d = τ − σ0, where σ0 =
max{σ|σ
τ ≤ PRR 0}.
1) If d ≥ n, any n times consecutive attack is optimal, and the
corresponding cost is (4).
2) If d < n, the optimal attack schedule has the structure of (8),
where z0+z1+z2+z3 +(s1 +s2)σ0 = T −n, and s1 +s2 = m,
where m is the quotient of n/d and r is the remainder. The
corresponding cost is
T r(J a )PRR
max = 1
T {m
dX
i=1
T r[hi (α, P )] +
rX
i=1
T r[hi (α, P )]}
+T − nα
T T r(P ).
Proof: See the Appendix.
Remark 4.2: In Problem 4.1, the attacker can completely avoid the
given IDS mechanism. However, this attack schedule seems too cau-
tious from an adventurous attacker’s point of view. If the adventurous
5By utilizing the pseudo-random sequence, the sensor and estimator may
implement channel hopping once the alarm is triggered [21]. However, the
attacker can detect such channel switch by detecting the alarm signal, and
search the new communication channel by scanning the wireless spectrum. In
this way, the attacker can learn the alarm bound through statistical analysis,
and follow the design against such IDS mechanism.
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015 3
B. Optimal attack schedule design
Now we are ready to present the optimal attack schedule for
Problem 2.1.
Theorem 3.1: The optimal attack schedule that solves Problem 2.1
is anyone that belongs to γn , and the corresponding cost is given by
T r(J a )max = 1
T
nX
i=1
T r[hi (α, P )] +T − nα
T T r(P ), (4)
where hi (α, P ) = [(n − i)(αi − αi+1 ) + αi ]hi (P ).
Proof: A direct result from Property 3.3 2) and 3).
As a byproduct, we can obtain the worst attack strategy which
minimizes the expected average error covariance.
Problem 3.1:
min
γ∈Γ T r[Ja (γ)],
s.t. k γ k0= n,
The solution of Problem 3.1 is given by the following theorem.
Theorem 3.2: 1) If n ≤ 1
2 T , an optimal solution for Problem 3.1
is anyone in γ1⊕1⊕···⊕1 , and the corresponding cost is given by
T r(J a )min = T − nα
T T r(P ) +nα
T T r[h(P )]. (5)
2) If n > 1
2 T , an optimal solution for Problem 3.1 is
((1 · · · 1
| {z }
z times
0) · · · (1 · · · 1
| {z }
z times
0)
| {z }
r 1 times
( 1 · · · 1
| {z }
m 1 times
0 1 · · · 1
| {z }
m 2 times
) (0 1 · · · 1
| {z }
z times
) · · · (0 1 · · · 1
| {z }
z times
)
| {z }
r 2 times
),
where r1 +r2 = T −n−1, z = ⌊ n
T−n ⌋,3 and m1 = m2 = m
2 if m is
even, m1 = ⌊ m
2 ⌋, m2 = m−m1 or m1 = ⌊ m
2 ⌋ + 1, m2 = m−m1
if m is odd, with m = z + [n mod (T − n)].4 The resulting cost is
T r(J a )min = 1
T T r{(T − n − 1)
zX
i=1
hi (α, P ) +
m 1X
i=1
hi (α, P )
+
m 2X
i=1
hi (α, P ) + [(T − n) + m(1 − α)
+z(1 − α)(T − n − 1)]P }, (6)
where hi (α, P ) = [(n − i)(αi − αi+1 ) + αi ]hi (P ).
Proof: A direct result from Property 3.3 3) and 4).
From the above two theorems, one can see that grouping the
attacks together leads to maximal attacking effect, while separating
the attacks as uniformly as possible leads to the minimal degradation.
Thus the results can be viewed as the upper and lower bound of the
damage an arbitrary attack schedule can make.
IV. OPTIMAL ATTACK SCHEDULES AGAINST A GIVEN IDS
The aforementioned problems are discussed under the assumption
that the channel is perfect and there is no defensive measure. In
practical applications, when the estimator considers unknown factors
from environment changes or adversary’s intrusion, which may lead
to data drops, a detector is often designed at the receiver side as a
first step to reduce the effectiveness of these factors. For example,
packet reception rate ( PRR ) at the receiver side is proposed as the
criteria for intrusion detection in [19]. PRR is the rate of packets
reception that are successfully delivered to the estimator compared
to the number of packets that have been sent out by the sensor.
3⌊x⌋ is floor function, which is defined as the largest integer that is less
than real number x.
4mod is defined as modulo operation, i.e., n mod m is the remainder in
division n
m , where n and m are two positive integer.
In practice, the PRR can be computed for a given length of a time
window τ, i.e., PRR = σ
τ , where σ is the packet reception numbers
in the time window. If the PRR is too small, the detector will deduce
that there may exist an attacker, which triggers an alarm to alert
the sensor. Then the sensor can use channel hopping technology to
guarantee the packet can be received by the remote estimator [20]. In
this paper, we assume that the alarm is triggered if PRR ≤ PRR 0,
where PRR 0 is a given alarm bound. 5
Fig. 2. Schematic of attack on the network against state estimation with an
intrusion detector.
Before introducing the attack schedule against the IDS mechanism,
we present a property to help formulate the attack optimization
problem.
Property 4.1: The alarm triggering condition PRR ≤ PRR 0 is
equivalent to Pk h d(P ), k = 1, 2, . . . , T, where d = τ − σ0,
σ0 = max{σ|σ
τ ≤ PRR 0}.
Proof: See the Appendix.
Remark 4.1: From Property 4.1, any attack schedule with at most
d times consecutive attack, i.e., P k+τ
i=k+1 γi ≤ d, k = 0, 1, . . . , T −τ,
can guarantee that the attack action will not be detected by the esti-
mator. In fact, time window τ and threshold PRR 0 can be evaluated
by the attacker when he eavesdrops the transmission channels before
taking attack actions.
In order not to be detected by IDS, we consider Problem 2.1 with
an additional constraint, i.e.,
Problem 4.1:
max
γ∈Γ T r[Ja (γ)],
s.t. k γ k0= n,
k+τX
i=k+1
γi ≤ d, k ∈ [0, T − τ ]. (7)
The following result presents the optimal solution to Problem 4.1.
Theorem 4.1: Consider Problem 4.1. Let d = τ − σ0, where σ0 =
max{σ|σ
τ ≤ PRR 0}.
1) If d ≥ n, any n times consecutive attack is optimal, and the
corresponding cost is (4).
2) If d < n, the optimal attack schedule has the structure of (8),
where z0+z1+z2+z3 +(s1 +s2)σ0 = T −n, and s1 +s2 = m,
where m is the quotient of n/d and r is the remainder. The
corresponding cost is
T r(J a )PRR
max = 1
T {m
dX
i=1
T r[hi (α, P )] +
rX
i=1
T r[hi (α, P )]}
+T − nα
T T r(P ).
Proof: See the Appendix.
Remark 4.2: In Problem 4.1, the attacker can completely avoid the
given IDS mechanism. However, this attack schedule seems too cau-
tious from an adventurous attacker’s point of view. If the adventurous
5By utilizing the pseudo-random sequence, the sensor and estimator may
implement channel hopping once the alarm is triggered [21]. However, the
attacker can detect such channel switch by detecting the alarm signal, and
search the new communication channel by scanning the wireless spectrum. In
this way, the attacker can learn the alarm bound through statistical analysis,
and follow the design against such IDS mechanism.
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

0018-9286 (c) 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
4 IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015
((0 · · · 0| {z }
z0 times
) (1 · · · 1| {z }
d times
0 · · · 0| {z }
σ0 times
) · · · (1 · · · 1| {z }
d times
0 · · · 0| {z }
σ0 times
)
| {z }
s1 times
(0 · · · 0| {z }
z1 times
1 · · · 1| {z }
r times
0 · · · 0| {z }
z2 times
) (0 · · · 0| {z }
σ0 times
1 · · · 1| {z }
d times
) · · · (0 · · · 0| {z }
σ0 times
1 · · · 1| {z }
d times
)
| {z }
s2 times
(0 · · · 0| {z }
z3 times
)), (8)
attacker still decides to use an attack schedule proposed in Theorem
3.1, the probability of being detected is P
k>d Ck
τ ατ−k (1 − α)k if
n > τ, and is P
k>d Ck
n αn−k (1 − α)k if n ≤ τ.
V. OPTIMAL ATTACK SCHEDULES WITH SENSOR ’S ENERGY
CONSTRAINT
The aforementioned problems are discussed under the assumption
that the sensor has sufficent energy to transmit throughout the entire
time horizon. When the sensor’s energy is also limited and cannot
transmit all the time, the attacker needs to change the attacking
schedule. Here we assume that the sensor and the estimator do not
know the existence of the attacker.
Some literatures have focused on sensor scheduling and optimal
state estimation in a lossy network environment [18], [22]–[25].
Sinopoli et. al. studied the problem of state estimation using Kalman
filtering in an i.i.d. packet-dropping network [22]. Reference [23]
studied optimal state estimation and optimal LQG controller de-
sign over an intermittent packet-dropping network. Shi et al. [18]
investigated sensor scheduling strategies to minimize the average
estimation error under energy constraint. Mo et al. [24] provided
a stochastic sensor selection scheme to minimize the asymptotic
expected estimation error covariance due to the energy constraint. You
et. al. [25] investigated the stability of the mean estimation error over
a network subject to Markovian packet losses. More related works
can be found in the reference therein. However, these literatures have
not considered the state estimation quality when a DoS attacker jams
the wireless channel and this shortage motivates us to study the
subsequent problem.
Denote ϑk = 1 or 0 as the sensor’s transmission decision variable
at time k, and ϑ as a scheduling scheme that defines ϑk at each k.
Θ is the set of the sensor’s transmission schedules. We assume that
the sensor has energy constraint with k ϑ k0= N and we consider
the following problem in this section.
Problem 5.1:
max
γ∈Γ min
ϑ∈Θ T r[Ja (ϑ, γ)], (9)
s.t. k ϑ k0= N, (10)
k γ k0= n. (11)
From [18], we have the following property:
Property 5.1: Let q = ⌊T
N ⌋.
1) If N < 1
2 T , the optimal sensor schedule ϑ∗ ∈ Θ that
minimizes the T r(J a ) has following structure
(1 0 . . . 0| {z }
τ1 times
)(1 0 . . . 0| {z }
τ2 times
) . . . (1 0 . . . 0| {z }
τN times
), (12)
in which there are T − qN times τi = q and (q + 1)N − T
times τi = q − 1in {τi , i = 1, 2, . . . , N }.
2) If N ≥ 1
2 T , ϑ∗ has structure (12) with T − N times τi = 1
and 2N − T times τi = 0 in {τi , i = 1, 2, . . . , N }.
Here we assume that the attacker obtains the sensor’s transmission
strategy by eavesdropping the transmission channel over a long period
before starting its attack action. We denote t(i) , i = 1, 2, . . . , Nas
the sensor’s data transmission time. If n ≥ N , it is obvious that
optimal attack schedule is taking actions at full transmission time
t(i) , i = 1, 2, . . . , N. Thus we only need to consider Problem 5.1 for
n < N hereinafter.
Theorem 5.1: Consider Problem 5.1 with n < N.
1) When N < 1
2 T and the sensor’s schedule ϑ∗ has the structure
(1 0 . . . 0| {z }
τ times
)(1 0 . . . 0| {z }
τ times
) . . . (1 0 . . . 0| {z }
τ times
), the optimal attack schedules
are given by γt(k) = 1, k = i + 1, i + 2, . . . , i + n, and γk = 0
otherwise. The corresponding cost is given by
T r(J a )max = 1
T
nX
i=1
T r[hi (α, ∆τ )] + N − nα
T T r(∆τ ),
where hi (α, ∆τ ) = [(n − i)(αi − αi+1 ) + αi ]hi (∆ τ ).
2) When N ≥ 1
2 T, α = 1 and the sensor’s schedule ϑ∗ has the
structure (1 . . . 1| {z }
δ times
0)(1 . . . 1| {z }
δ times
0) . . . (1 . . . 1| {z }
δ times
0), the optimal attack
schedules γ∗ are given by γt(k) = 1, k = i+1, i+2, . . . , i+n,
and γk = 0 otherwise. The corresponding cost is given by
T r(J a )max = 1
T T r
h
(N − n)P + (T − N − b)h(P )
+
n+bX
i=1
hi (P )
i
, (13)
where n = δb + b0 with 0 ≤ b0 < b.
Proof: 1) The proof is similar to that of Theorem 3.1. The only
difference is that we replace P by ∆ τ .
2) One can easily obtain that the resulting cost under the attack
schedule γ∗ is (13). For an arbitrary attack schedule γ, we have
T r(J a (γ)) = 1
T T r
h
(N − n)P + m1h(P ) +
m 2X
i=1
tiX
j=1
hj (P )
i
,
where ti is the length of i-th (i = 1, 2, . . . , m2) attack period [si +
1, si + ti ] which satisfies ϑsi = 1, γsi = 0, ϑsi +t i = 1, γsi +t i = 0,
and ϑk = 1, γk = 1or ϑk = 0, γk = 0for k = si +2, . . . , si +ti −1,
(N − n) + m1 + P m 2
i=1 ti = T and P m 2
i=1 ti ≤ n + b. Then we have
T r(J a (γ∗)) − T r(Ja (γ))
= 1
T T r
hn+bX
i=1
hi (P ) −
m 2X
i=1
tiX
j=1
hj (P ) − [m1 − (T − N − b)]h(P )
i
> 0,
which completes the proof.
Example 5.1: (1) Consider the Problem 5.1 for N < 1
2 T
with T = 12, N = 4, n = 2, τ = 2 . From Property
5.1, one notes that the optimal sensor transmission schedule is
ϑ∗ = (100)(100)(100)(100). Then we can obtain three opti-
mal attack schedules (100)(100)(000)(000), (000)(100)(100)(000),
(000)(000)(100)(100). (2) For N ≥ 1
2 T , consider T = 12, N =
9, n = 6, δ = 3. From Property 5.1, the optimal sensor transmis-
sion schedule is ϑ∗ = (1110)(1110)(1110). Then we obtain four
optimal attack schedules (1110)(1110)(0000), (0110)(1110)(1000),
(0010)(1110)(1100), (0000)(1110)(1110).
Remark 5.1: In Theorem 5.1 we study some special cases of
Problem 5.1, and obtain the optimal attack schedules. Note that these
schedules only depend on the sensor transmission schedule ϑ∗ rather
than on the system parameters. Thus the attacker can run his optimal
attack schedules when he obtains the sensor’s transmission schedule
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
4 IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015
((0 · · · 0| {z }
z0 times
) (1 · · · 1| {z }
d times
0 · · · 0| {z }
σ0 times
) · · · (1 · · · 1| {z }
d times
0 · · · 0| {z }
σ0 times
)
| {z }
s1 times
(0 · · · 0| {z }
z1 times
1 · · · 1| {z }
r times
0 · · · 0| {z }
z2 times
) (0 · · · 0| {z }
σ0 times
1 · · · 1| {z }
d times
) · · · (0 · · · 0| {z }
σ0 times
1 · · · 1| {z }
d times
)
| {z }
s2 times
(0 · · · 0| {z }
z3 times
)), (8)
attacker still decides to use an attack schedule proposed in Theorem
3.1, the probability of being detected is P
k>d Ck
τ ατ−k (1 − α)k if
n > τ, and is P
k>d Ck
n αn−k (1 − α)k if n ≤ τ.
V. OPTIMAL ATTACK SCHEDULES WITH SENSOR ’S ENERGY
CONSTRAINT
The aforementioned problems are discussed under the assumption
that the sensor has sufficent energy to transmit throughout the entire
time horizon. When the sensor’s energy is also limited and cannot
transmit all the time, the attacker needs to change the attacking
schedule. Here we assume that the sensor and the estimator do not
know the existence of the attacker.
Some literatures have focused on sensor scheduling and optimal
state estimation in a lossy network environment [18], [22]–[25].
Sinopoli et. al. studied the problem of state estimation using Kalman
filtering in an i.i.d. packet-dropping network [22]. Reference [23]
studied optimal state estimation and optimal LQG controller de-
sign over an intermittent packet-dropping network. Shi et al. [18]
investigated sensor scheduling strategies to minimize the average
estimation error under energy constraint. Mo et al. [24] provided
a stochastic sensor selection scheme to minimize the asymptotic
expected estimation error covariance due to the energy constraint. You
et. al. [25] investigated the stability of the mean estimation error over
a network subject to Markovian packet losses. More related works
can be found in the reference therein. However, these literatures have
not considered the state estimation quality when a DoS attacker jams
the wireless channel and this shortage motivates us to study the
subsequent problem.
Denote ϑk = 1 or 0 as the sensor’s transmission decision variable
at time k, and ϑ as a scheduling scheme that defines ϑk at each k.
Θ is the set of the sensor’s transmission schedules. We assume that
the sensor has energy constraint with k ϑ k0= N and we consider
the following problem in this section.
Problem 5.1:
max
γ∈Γ min
ϑ∈Θ T r[Ja (ϑ, γ)], (9)
s.t. k ϑ k0= N, (10)
k γ k0= n. (11)
From [18], we have the following property:
Property 5.1: Let q = ⌊T
N ⌋.
1) If N < 1
2 T , the optimal sensor schedule ϑ∗ ∈ Θ that
minimizes the T r(J a ) has following structure
(1 0 . . . 0| {z }
τ1 times
)(1 0 . . . 0| {z }
τ2 times
) . . . (1 0 . . . 0| {z }
τN times
), (12)
in which there are T − qN times τi = q and (q + 1)N − T
times τi = q − 1in {τi , i = 1, 2, . . . , N }.
2) If N ≥ 1
2 T , ϑ∗ has structure (12) with T − N times τi = 1
and 2N − T times τi = 0 in {τi , i = 1, 2, . . . , N }.
Here we assume that the attacker obtains the sensor’s transmission
strategy by eavesdropping the transmission channel over a long period
before starting its attack action. We denote t(i) , i = 1, 2, . . . , Nas
the sensor’s data transmission time. If n ≥ N , it is obvious that
optimal attack schedule is taking actions at full transmission time
t(i) , i = 1, 2, . . . , N. Thus we only need to consider Problem 5.1 for
n < N hereinafter.
Theorem 5.1: Consider Problem 5.1 with n < N.
1) When N < 1
2 T and the sensor’s schedule ϑ∗ has the structure
(1 0 . . . 0| {z }
τ times
)(1 0 . . . 0| {z }
τ times
) . . . (1 0 . . . 0| {z }
τ times
), the optimal attack schedules
are given by γt(k) = 1, k = i + 1, i + 2, . . . , i + n, and γk = 0
otherwise. The corresponding cost is given by
T r(J a )max = 1
T
nX
i=1
T r[hi (α, ∆τ )] + N − nα
T T r(∆τ ),
where hi (α, ∆τ ) = [(n − i)(αi − αi+1 ) + αi ]hi (∆ τ ).
2) When N ≥ 1
2 T, α = 1 and the sensor’s schedule ϑ∗ has the
structure (1 . . . 1| {z }
δ times
0)(1 . . . 1| {z }
δ times
0) . . . (1 . . . 1| {z }
δ times
0), the optimal attack
schedules γ∗ are given by γt(k) = 1, k = i+1, i+2, . . . , i+n,
and γk = 0 otherwise. The corresponding cost is given by
T r(J a )max = 1
T T r
h
(N − n)P + (T − N − b)h(P )
+
n+bX
i=1
hi (P )
i
, (13)
where n = δb + b0 with 0 ≤ b0 < b.
Proof: 1) The proof is similar to that of Theorem 3.1. The only
difference is that we replace P by ∆ τ .
2) One can easily obtain that the resulting cost under the attack
schedule γ∗ is (13). For an arbitrary attack schedule γ, we have
T r(J a (γ)) = 1
T T r
h
(N − n)P + m1h(P ) +
m 2X
i=1
tiX
j=1
hj (P )
i
,
where ti is the length of i-th (i = 1, 2, . . . , m2) attack period [si +
1, si + ti ] which satisfies ϑsi = 1, γsi = 0, ϑsi +t i = 1, γsi +t i = 0,
and ϑk = 1, γk = 1or ϑk = 0, γk = 0for k = si +2, . . . , si +ti −1,
(N − n) + m1 + P m 2
i=1 ti = T and P m 2
i=1 ti ≤ n + b. Then we have
T r(J a (γ∗)) − T r(Ja (γ))
= 1
T T r
hn+bX
i=1
hi (P ) −
m 2X
i=1
tiX
j=1
hj (P ) − [m1 − (T − N − b)]h(P )
i
> 0,
which completes the proof.
Example 5.1: (1) Consider the Problem 5.1 for N < 1
2 T
with T = 12, N = 4, n = 2, τ = 2 . From Property
5.1, one notes that the optimal sensor transmission schedule is
ϑ∗ = (100)(100)(100)(100). Then we can obtain three opti-
mal attack schedules (100)(100)(000)(000), (000)(100)(100)(000),
(000)(000)(100)(100). (2) For N ≥ 1
2 T , consider T = 12, N =
9, n = 6, δ = 3. From Property 5.1, the optimal sensor transmis-
sion schedule is ϑ∗ = (1110)(1110)(1110). Then we obtain four
optimal attack schedules (1110)(1110)(0000), (0110)(1110)(1000),
(0010)(1110)(1100), (0000)(1110)(1110).
Remark 5.1: In Theorem 5.1 we study some special cases of
Problem 5.1, and obtain the optimal attack schedules. Note that these
schedules only depend on the sensor transmission schedule ϑ∗ rather
than on the system parameters. Thus the attacker can run his optimal
attack schedules when he obtains the sensor’s transmission schedule
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
0018-9286 (c) 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015 5
ϑ∗. The general cases of Problem 5.1, however, are complicated since
the optimal attack schedules depend on sensor transmission schedule
ϑ, the system parameters, and the attack successful probability. An
example is given in Section VI (Fig. 5) to illustrate this.
Remark 5.2: In many situations, the expected terminal estimation
error, i.e., J T = E[PT ] is considered as another important system
performance index [26]. When the attacker tries to maximize the
trace of expected terminal estimation error covariance, one can see
that the optimal attack schedule is to consecutively attack at time k =
T − n + 1, T − n + 2, . . . , T. If the detector with (7) is embedded in
estimator, any feasible attack schedule with γT −d = 0, γk = 1, k =
T − d + 1, T − d + 2, . . . , Tis optimal. If the sensor also has energy
constraint (10) with N > n , we can prove that the optimal attack
schedule is γ(k) = 1, k = T − n + 1, T − n + 2, . . . , T, γk = 0
otherwise.
VI. EXAMPLES
Consider system (1) with
A = 1.2 0.1
0 1 , C = 1 0
0 1 , Σw = 1 0
0 2 , Σv = 0.5C.
The effects of different attack schedules are evaluated.In Fig. 3,
where we examine the performance under different attack times
from 1 to 10 with T = 100, α = 1 . It can be seen that the
performance under the optimal attack schedules given by Theorem
3.1, i.e., T r(J a )max , increases rapidly with the allowable attack
times. T r(J a )min , which is under the attack schedule obtained in
Theorem 3.2, and T r(J a )PRR
max , which is under the attack schedule
given in Theorem 4.1 with PRR ≤ 3
7 , grow much slower than
T r(J a )max . It also can be found that T r(J a )max and T r(J a )PRR
max
are overlapping since they have the same optimal attack schedule set
γn when n ≤ 4 . But if n > 4 , T r(J a )PRR
max grows much slower
than T r(J a )max as the attack schedules need to be re-designed
under the given intrusion detection mechanism. It also can been seen
that the attack effectiveness is significantly reduced by this detection
constraint.
1 2 3 4 5 6 7 8 9 10
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
n
T r(Ja)
T r(Ja)max
T r(Ja)PRR
max
T r(Ja)min
T r(Ja)no
Fig. 3. Illustrating example on T r(J) under different attack schedules with
varying attack times ( T = 100, α = 1).
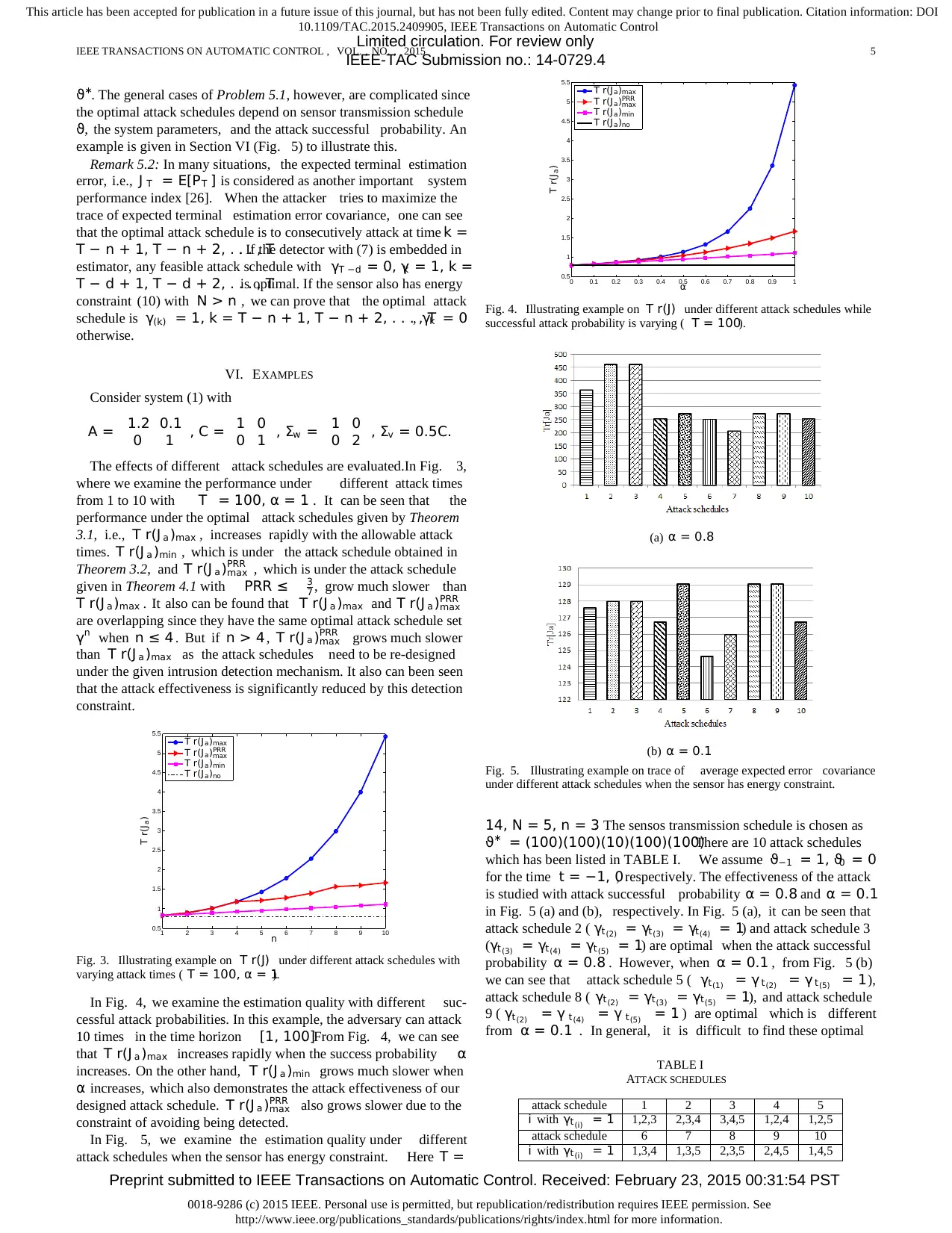
In Fig. 4, we examine the estimation quality with different suc-
cessful attack probabilities. In this example, the adversary can attack
10 times in the time horizon [1, 100]. From Fig. 4, we can see
that T r(J a )max increases rapidly when the success probability α
increases. On the other hand, T r(J a )min grows much slower when
α increases, which also demonstrates the attack effectiveness of our
designed attack schedule. T r(J a )PRR
max also grows slower due to the
constraint of avoiding being detected.
In Fig. 5, we examine the estimation quality under different
attack schedules when the sensor has energy constraint. Here T =
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
α
T r(Ja)
T r(Ja)max
T r(Ja)PRR
max
T r(Ja)min
T r(Ja)no
Fig. 4. Illustrating example on T r(J) under different attack schedules while
successful attack probability is varying ( T = 100).
(a) α = 0.8
(b) α = 0.1
Fig. 5. Illustrating example on trace of average expected error covariance
under different attack schedules when the sensor has energy constraint.
14, N = 5, n = 3. The sensos transmission schedule is chosen as
ϑ∗ = (100)(100)(10)(100)(100). There are 10 attack schedules
which has been listed in TABLE I. We assume ϑ−1 = 1, ϑ0 = 0
for the time t = −1, 0, respectively. The effectiveness of the attack
is studied with attack successful probability α = 0.8 and α = 0.1
in Fig. 5 (a) and (b), respectively. In Fig. 5 (a), it can be seen that
attack schedule 2 ( γt(2) = γt(3) = γt(4) = 1) and attack schedule 3
(γt(3) = γt(4) = γt(5) = 1) are optimal when the attack successful
probability α = 0.8 . However, when α = 0.1 , from Fig. 5 (b)
we can see that attack schedule 5 ( γt(1) = γ t(2) = γ t(5) = 1),
attack schedule 8 ( γt(2) = γt(3) = γt(5) = 1), and attack schedule
9 ( γt(2) = γ t(4) = γ t(5) = 1 ) are optimal which is different
from α = 0.1 . In general, it is difficult to find these optimal
TABLE I
ATTACK SCHEDULES
attack schedule 1 2 3 4 5
i with γt(i) = 1 1,2,3 2,3,4 3,4,5 1,2,4 1,2,5
attack schedule 6 7 8 9 10
i with γt(i) = 1 1,3,4 1,3,5 2,3,5 2,4,5 1,4,5
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015 5
ϑ∗. The general cases of Problem 5.1, however, are complicated since
the optimal attack schedules depend on sensor transmission schedule
ϑ, the system parameters, and the attack successful probability. An
example is given in Section VI (Fig. 5) to illustrate this.
Remark 5.2: In many situations, the expected terminal estimation
error, i.e., J T = E[PT ] is considered as another important system
performance index [26]. When the attacker tries to maximize the
trace of expected terminal estimation error covariance, one can see
that the optimal attack schedule is to consecutively attack at time k =
T − n + 1, T − n + 2, . . . , T. If the detector with (7) is embedded in
estimator, any feasible attack schedule with γT −d = 0, γk = 1, k =
T − d + 1, T − d + 2, . . . , Tis optimal. If the sensor also has energy
constraint (10) with N > n , we can prove that the optimal attack
schedule is γ(k) = 1, k = T − n + 1, T − n + 2, . . . , T, γk = 0
otherwise.
VI. EXAMPLES
Consider system (1) with
A = 1.2 0.1
0 1 , C = 1 0
0 1 , Σw = 1 0
0 2 , Σv = 0.5C.
The effects of different attack schedules are evaluated.In Fig. 3,
where we examine the performance under different attack times
from 1 to 10 with T = 100, α = 1 . It can be seen that the
performance under the optimal attack schedules given by Theorem
3.1, i.e., T r(J a )max , increases rapidly with the allowable attack
times. T r(J a )min , which is under the attack schedule obtained in
Theorem 3.2, and T r(J a )PRR
max , which is under the attack schedule
given in Theorem 4.1 with PRR ≤ 3
7 , grow much slower than
T r(J a )max . It also can be found that T r(J a )max and T r(J a )PRR
max
are overlapping since they have the same optimal attack schedule set
γn when n ≤ 4 . But if n > 4 , T r(J a )PRR
max grows much slower
than T r(J a )max as the attack schedules need to be re-designed
under the given intrusion detection mechanism. It also can been seen
that the attack effectiveness is significantly reduced by this detection
constraint.
1 2 3 4 5 6 7 8 9 10
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
n
T r(Ja)
T r(Ja)max
T r(Ja)PRR
max
T r(Ja)min
T r(Ja)no
Fig. 3. Illustrating example on T r(J) under different attack schedules with
varying attack times ( T = 100, α = 1).
In Fig. 4, we examine the estimation quality with different suc-
cessful attack probabilities. In this example, the adversary can attack
10 times in the time horizon [1, 100]. From Fig. 4, we can see
that T r(J a )max increases rapidly when the success probability α
increases. On the other hand, T r(J a )min grows much slower when
α increases, which also demonstrates the attack effectiveness of our
designed attack schedule. T r(J a )PRR
max also grows slower due to the
constraint of avoiding being detected.
In Fig. 5, we examine the estimation quality under different
attack schedules when the sensor has energy constraint. Here T =
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
α
T r(Ja)
T r(Ja)max
T r(Ja)PRR
max
T r(Ja)min
T r(Ja)no
Fig. 4. Illustrating example on T r(J) under different attack schedules while
successful attack probability is varying ( T = 100).
(a) α = 0.8
(b) α = 0.1
Fig. 5. Illustrating example on trace of average expected error covariance
under different attack schedules when the sensor has energy constraint.
14, N = 5, n = 3. The sensos transmission schedule is chosen as
ϑ∗ = (100)(100)(10)(100)(100). There are 10 attack schedules
which has been listed in TABLE I. We assume ϑ−1 = 1, ϑ0 = 0
for the time t = −1, 0, respectively. The effectiveness of the attack
is studied with attack successful probability α = 0.8 and α = 0.1
in Fig. 5 (a) and (b), respectively. In Fig. 5 (a), it can be seen that
attack schedule 2 ( γt(2) = γt(3) = γt(4) = 1) and attack schedule 3
(γt(3) = γt(4) = γt(5) = 1) are optimal when the attack successful
probability α = 0.8 . However, when α = 0.1 , from Fig. 5 (b)
we can see that attack schedule 5 ( γt(1) = γ t(2) = γ t(5) = 1),
attack schedule 8 ( γt(2) = γt(3) = γt(5) = 1), and attack schedule
9 ( γt(2) = γ t(4) = γ t(5) = 1 ) are optimal which is different
from α = 0.1 . In general, it is difficult to find these optimal
TABLE I
ATTACK SCHEDULES
attack schedule 1 2 3 4 5
i with γt(i) = 1 1,2,3 2,3,4 3,4,5 1,2,4 1,2,5
attack schedule 6 7 8 9 10
i with γt(i) = 1 1,3,4 1,3,5 2,3,5 2,4,5 1,4,5
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST

0018-9286 (c) 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
6 IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015
attack schedules explicitly. On the other hand, the suboptimal attack
schedules 1, 2, 3 only depend on sensor transmission schedule ϑ, and
can be easily obtained.
VII. CONCLUSION
In this paper, we considered optimal attack scheduling against
remote state estimation through a wireless channel. We proved that
consecutive attacks maximize the expected average error covariance.
We also showed that when the attacks are separated uniformly,
the attack effect on the estimation quality is minimum. We further
proposed the optimal attack schedules when a special intrusion
detection mechanism in the estimator is available. We finally studied
the optimal attack schedules when both the sensor and the attacker
have energy constraints. It is interesting but challenging to find a
closed-form solution for optimal attack scheduling over packet lossy
network environment. This will be left as a future work. We will
also formulate the infinite-horizon attack model and study the optimal
attack schedule in the future. It is also interesting to consider optimal
defensive strategies assuming that the sensor knows the existence of
the attacker. We will further validate our results using some physical
experiments, and consider optimal attack scheduling against feedback
control and evaluating the corresponding effectiveness.
APPENDIX
A. Proof of Property 3.3
Proof: 1) We have J (m 2 )
a − J (m 1 )
a = 1
T
m 2P
k=m 1 +1
E[Pk ] ≥ 0.
2) We have
J (n)
a − J (n 1 ⊕n 2 )
a = 1
T
n nX
k=n 1 +1
n 1X
i=0
E[Pk |Pn 1 = hi (P )]
·P r{Pn 1 = hi (P )} −
nX
k=n 1 +1
E[Pk |Pn 1 = P ]
o
≥ 0,
in which the last inequation is from statement 1) of Property 3.2.
3) The proof of this result is similar to 2). Due to the limitation
of space, it is omitted.
4) It suffices to proveJ (m 1 ⊕m 2 )
a ≤ J ((m 1 +1)⊕(m 2 −1))
a , with m1 ≥
m2. In fact, J ((m 1 +1)⊕(m 2 −1))
a − J (m 1 ⊕m 2 )
a = 1
T {E[Ps+m 1 +1 ] −
E[Ps+m 2 ]} ≥ 0. The last inequality is from Property 3.2 2).
B. Proof of Property 4.1
Proof: Alarm triggering condition PRR ≤ PRR 0 is equivalent
to σ ≤ σ0. Thus it is also equivalent to that the packets drop number
dnum in any time window is larger than d = τ − τ0, i.e., dnum > d.
In order to obtain the result, we prove by contradiction, i.e.,
dnum ≤ d is equivalent to Pk ≤ hd(P ), which clearly holds.
C. Proof of Theorem 4.1
Proof: If d ≥ n, any n times consecutive attack schedules satisfy
the conditions Pk ≤ hd(P ), k = 1, 2, . . . , T. Thus these schedules
are optimal for Problem 4.1 when d ≥ n . From Remark 4.1 and
statements 1) and 3) of Property 3.3, we can obtain that optimal
attack schedule has the structure (8) if d < n.
REFERENCES
[1] H. Zhang, P. Cheng, L. Shi, and J. Chen, “Optimal DoS attack policy
against remote state estimation,” in Proceedings of IEEE Conference on
Decision and Control (CDC), 2013, pp. 5444–5449.
[2] ——, “Optimal Denial-of-Service attack scheduling in cyber-physical
systems,” Zhejiang University, Tech. Rep., Jan. 2015. [Online].
Available: http://www.sensornet.cn/heng/Heng estimation Full.pdf
[3] Y. Mo, T. Kim, K. Brancik, D. Dickinson, H. Lee, A. Perrig, and
B. Sinopoli, “Cyber–physical security of a smart grid infrastructure,”
Proceedings of the IEEE, no. 99, pp. 1–15, 2012.
[4] S. Amin, X. Litrico, S. S. Sastry, and A. M. Bayen, “Cyber security
of water scada systems-part i: Analysis and experimentation of stealthy
deception attacks,” IEEE Transactions on Control Systems Technology,
vol. 21, no. 5, pp. 1963–1970, 2013.
[5] H. Zhang, Y. Shu, P. Cheng, and J. Chen, “Privacy and performance
trade-off in cyber-physical systems,” IEEE Networks, to appear.
[6] J. Farwell and R. Rohozinski, “Stuxnet and the future of cyber war,”
Survival, vol. 53, no. 1, pp. 23–40, 2011.
[7] S. Sundaram and C. N. Hadjicostis, “Distributed function calculation
via linear iterative strategies in the presence of malicious agents,” IEEE
Transactions on Automatic Control, vol. 56, no. 7, pp. 1495–1508, 2011.
[8] A. Teixeira, D. P´erez, H. Sandberg, and K. H. Johansson, “Attack models
and scenarios for networked control systems,” in Proceedings of the 1st
international conference on High Confidence Networked Systems, 2012,
pp. 55–64.
[9] S. Amin, A. C´ardenas, and S. Sastry, “Safe and secure networked control
systems under denial-of-service attacks,” Hybrid Systems: Computation
and Control, pp. 31–45, 2009.
[10] M. Zuba, Z. Shi, Z. Peng, and J. Cui, “Launching Denial-of-Service
jamming attacks in underwater sensor networks,” in Proceedings of the
6th ACM International Workshop on Underwater Networks, 2011, p. 12.
[11] Y. Law, M. Palaniswami, L. Hoesel, J. Doumen, P. Hartel, and
P. Havinga, “Energy-efficient link-layer jamming attacks against wireless
sensor network mac protocols,” ACM Transactions on Sensor Networks,
vol. 5, no. 1, p. 6, 2009.
[12] T. Kavitha and D. Sridharan, “Security vulnerabilities in wireless sensor
networks: A survey,” Journal of information Assurance and Security,
vol. 5, no. 1, pp. 31–44, 2010.
[13] H. Zhang, P. Cheng, L. Shi, and J. Chen, “Optimal Denial-of-Service
attack scheduling against linear quadratic gaussian control,” in Proceed-
ings of American Control Conference (ACC), 2014, pp. 3996–4001.
[14] A. C´ardenas, S. Amin, and S. Sastry, “Research challenges for the
security of control systems,” in Proceedings of the 3rd conference on
Hot topics in security, 2008, pp. 1–6.
[15] R. Poisel, Modern communications jamming principles and techniques.
Artech House Publishers, 2011.
[16] G. Gu, X.-R. Cao, and H. Badr, “Generalized lqr control and kalman
filtering with relations to computations of inner-outer and spectral
factorizations,” IEEE Transactions on Automatic Control, vol. 51, no. 4,
pp. 595–605, 2006.
[17] L. Shi, P. Cheng, and J. Chen, “Optimal periodic sensor scheduling with
limited resources,” IEEE Transactions on Automatic Control, vol. 56,
no. 9, pp. 2190–2195, 2011.
[18] ——, “Sensor data scheduling for optimal state estimation with commu-
nication energy constraint,” Automatica, vol. 47, no. 8, pp. 1693–1698,
2011.
[19] Y. Ponomarchuk and D.-W. Seo, “Intrusion detection based on traffic
analysis in wireless sensor networks,” in Proceedings of Annual Wireless
and Optical Communications Conference, 2010, pp. 1–7.
[20] M. Sha, G. Hackmann, and C. Lu, “Arch: Practical channel hopping for
reliable home-area sensor networks,” in Proceedings of 17th IEEE Real-
Time and Embedded Technology and Applications Symposium, 2011, pp.
305–315.
[21] V. Navda, A. Bohra, S. Ganguly, and D. Rubenstein, “Using channel hop-
ping to increase 802.11 resilience to jamming attacks,” in Proceedings
of 26th IEEE International Conference on Computer Communications,
2007, pp. 2526–2530.
[22] B. Sinopoli, L. Schenato, M. Franceschetti, K. Poolla, M. Jordan,
and S. Sastry, “Kalman filtering with intermittent observations,” IEEE
Transactions on Automatic Control, vol. 49, no. 9, pp. 1453–1464, 2004.
[23] L. Schenato, B. Sinopoli, M. Franceschetti, K. Poolla, and S. S.
Sastry, “Foundations of control and estimation over lossy networks,”
Proceedings of the IEEE, vol. 95, no. 1, pp. 163–187, 2007.
[24] Y. Mo, E. Garone, A. Casavola, and B. Sinopoli, “Stochastic sensor
scheduling for energy constrained estimation in multi-hop wireless
sensor networks,” IEEE Transactions on Automatic Control, vol. 56,
no. 10, pp. 2489–2495, 2011.
[25] K. You, M. Fu, and L. Xie, “Mean square stability for kalman filtering
with markovian packet losses,” Automatica, vol. 47, pp. 2647–2657,
2011.
[26] L. Shi and L. Xie, “Optimal sensor power scheduling for state estimation
of Gauss–Markov systems over a packet-dropping network,” IEEE
Transactions on Signal Processing, vol. 60, no. 5, pp. 2701–2705, 2012.
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TAC.2015.2409905, IEEE Transactions on Automatic Control
6 IEEE TRANSACTIONS ON AUTOMATIC CONTROL , VOL. , NO. , 2015
attack schedules explicitly. On the other hand, the suboptimal attack
schedules 1, 2, 3 only depend on sensor transmission schedule ϑ, and
can be easily obtained.
VII. CONCLUSION
In this paper, we considered optimal attack scheduling against
remote state estimation through a wireless channel. We proved that
consecutive attacks maximize the expected average error covariance.
We also showed that when the attacks are separated uniformly,
the attack effect on the estimation quality is minimum. We further
proposed the optimal attack schedules when a special intrusion
detection mechanism in the estimator is available. We finally studied
the optimal attack schedules when both the sensor and the attacker
have energy constraints. It is interesting but challenging to find a
closed-form solution for optimal attack scheduling over packet lossy
network environment. This will be left as a future work. We will
also formulate the infinite-horizon attack model and study the optimal
attack schedule in the future. It is also interesting to consider optimal
defensive strategies assuming that the sensor knows the existence of
the attacker. We will further validate our results using some physical
experiments, and consider optimal attack scheduling against feedback
control and evaluating the corresponding effectiveness.
APPENDIX
A. Proof of Property 3.3
Proof: 1) We have J (m 2 )
a − J (m 1 )
a = 1
T
m 2P
k=m 1 +1
E[Pk ] ≥ 0.
2) We have
J (n)
a − J (n 1 ⊕n 2 )
a = 1
T
n nX
k=n 1 +1
n 1X
i=0
E[Pk |Pn 1 = hi (P )]
·P r{Pn 1 = hi (P )} −
nX
k=n 1 +1
E[Pk |Pn 1 = P ]
o
≥ 0,
in which the last inequation is from statement 1) of Property 3.2.
3) The proof of this result is similar to 2). Due to the limitation
of space, it is omitted.
4) It suffices to proveJ (m 1 ⊕m 2 )
a ≤ J ((m 1 +1)⊕(m 2 −1))
a , with m1 ≥
m2. In fact, J ((m 1 +1)⊕(m 2 −1))
a − J (m 1 ⊕m 2 )
a = 1
T {E[Ps+m 1 +1 ] −
E[Ps+m 2 ]} ≥ 0. The last inequality is from Property 3.2 2).
B. Proof of Property 4.1
Proof: Alarm triggering condition PRR ≤ PRR 0 is equivalent
to σ ≤ σ0. Thus it is also equivalent to that the packets drop number
dnum in any time window is larger than d = τ − τ0, i.e., dnum > d.
In order to obtain the result, we prove by contradiction, i.e.,
dnum ≤ d is equivalent to Pk ≤ hd(P ), which clearly holds.
C. Proof of Theorem 4.1
Proof: If d ≥ n, any n times consecutive attack schedules satisfy
the conditions Pk ≤ hd(P ), k = 1, 2, . . . , T. Thus these schedules
are optimal for Problem 4.1 when d ≥ n . From Remark 4.1 and
statements 1) and 3) of Property 3.3, we can obtain that optimal
attack schedule has the structure (8) if d < n.
REFERENCES
[1] H. Zhang, P. Cheng, L. Shi, and J. Chen, “Optimal DoS attack policy
against remote state estimation,” in Proceedings of IEEE Conference on
Decision and Control (CDC), 2013, pp. 5444–5449.
[2] ——, “Optimal Denial-of-Service attack scheduling in cyber-physical
systems,” Zhejiang University, Tech. Rep., Jan. 2015. [Online].
Available: http://www.sensornet.cn/heng/Heng estimation Full.pdf
[3] Y. Mo, T. Kim, K. Brancik, D. Dickinson, H. Lee, A. Perrig, and
B. Sinopoli, “Cyber–physical security of a smart grid infrastructure,”
Proceedings of the IEEE, no. 99, pp. 1–15, 2012.
[4] S. Amin, X. Litrico, S. S. Sastry, and A. M. Bayen, “Cyber security
of water scada systems-part i: Analysis and experimentation of stealthy
deception attacks,” IEEE Transactions on Control Systems Technology,
vol. 21, no. 5, pp. 1963–1970, 2013.
[5] H. Zhang, Y. Shu, P. Cheng, and J. Chen, “Privacy and performance
trade-off in cyber-physical systems,” IEEE Networks, to appear.
[6] J. Farwell and R. Rohozinski, “Stuxnet and the future of cyber war,”
Survival, vol. 53, no. 1, pp. 23–40, 2011.
[7] S. Sundaram and C. N. Hadjicostis, “Distributed function calculation
via linear iterative strategies in the presence of malicious agents,” IEEE
Transactions on Automatic Control, vol. 56, no. 7, pp. 1495–1508, 2011.
[8] A. Teixeira, D. P´erez, H. Sandberg, and K. H. Johansson, “Attack models
and scenarios for networked control systems,” in Proceedings of the 1st
international conference on High Confidence Networked Systems, 2012,
pp. 55–64.
[9] S. Amin, A. C´ardenas, and S. Sastry, “Safe and secure networked control
systems under denial-of-service attacks,” Hybrid Systems: Computation
and Control, pp. 31–45, 2009.
[10] M. Zuba, Z. Shi, Z. Peng, and J. Cui, “Launching Denial-of-Service
jamming attacks in underwater sensor networks,” in Proceedings of the
6th ACM International Workshop on Underwater Networks, 2011, p. 12.
[11] Y. Law, M. Palaniswami, L. Hoesel, J. Doumen, P. Hartel, and
P. Havinga, “Energy-efficient link-layer jamming attacks against wireless
sensor network mac protocols,” ACM Transactions on Sensor Networks,
vol. 5, no. 1, p. 6, 2009.
[12] T. Kavitha and D. Sridharan, “Security vulnerabilities in wireless sensor
networks: A survey,” Journal of information Assurance and Security,
vol. 5, no. 1, pp. 31–44, 2010.
[13] H. Zhang, P. Cheng, L. Shi, and J. Chen, “Optimal Denial-of-Service
attack scheduling against linear quadratic gaussian control,” in Proceed-
ings of American Control Conference (ACC), 2014, pp. 3996–4001.
[14] A. C´ardenas, S. Amin, and S. Sastry, “Research challenges for the
security of control systems,” in Proceedings of the 3rd conference on
Hot topics in security, 2008, pp. 1–6.
[15] R. Poisel, Modern communications jamming principles and techniques.
Artech House Publishers, 2011.
[16] G. Gu, X.-R. Cao, and H. Badr, “Generalized lqr control and kalman
filtering with relations to computations of inner-outer and spectral
factorizations,” IEEE Transactions on Automatic Control, vol. 51, no. 4,
pp. 595–605, 2006.
[17] L. Shi, P. Cheng, and J. Chen, “Optimal periodic sensor scheduling with
limited resources,” IEEE Transactions on Automatic Control, vol. 56,
no. 9, pp. 2190–2195, 2011.
[18] ——, “Sensor data scheduling for optimal state estimation with commu-
nication energy constraint,” Automatica, vol. 47, no. 8, pp. 1693–1698,
2011.
[19] Y. Ponomarchuk and D.-W. Seo, “Intrusion detection based on traffic
analysis in wireless sensor networks,” in Proceedings of Annual Wireless
and Optical Communications Conference, 2010, pp. 1–7.
[20] M. Sha, G. Hackmann, and C. Lu, “Arch: Practical channel hopping for
reliable home-area sensor networks,” in Proceedings of 17th IEEE Real-
Time and Embedded Technology and Applications Symposium, 2011, pp.
305–315.
[21] V. Navda, A. Bohra, S. Ganguly, and D. Rubenstein, “Using channel hop-
ping to increase 802.11 resilience to jamming attacks,” in Proceedings
of 26th IEEE International Conference on Computer Communications,
2007, pp. 2526–2530.
[22] B. Sinopoli, L. Schenato, M. Franceschetti, K. Poolla, M. Jordan,
and S. Sastry, “Kalman filtering with intermittent observations,” IEEE
Transactions on Automatic Control, vol. 49, no. 9, pp. 1453–1464, 2004.
[23] L. Schenato, B. Sinopoli, M. Franceschetti, K. Poolla, and S. S.
Sastry, “Foundations of control and estimation over lossy networks,”
Proceedings of the IEEE, vol. 95, no. 1, pp. 163–187, 2007.
[24] Y. Mo, E. Garone, A. Casavola, and B. Sinopoli, “Stochastic sensor
scheduling for energy constrained estimation in multi-hop wireless
sensor networks,” IEEE Transactions on Automatic Control, vol. 56,
no. 10, pp. 2489–2495, 2011.
[25] K. You, M. Fu, and L. Xie, “Mean square stability for kalman filtering
with markovian packet losses,” Automatica, vol. 47, pp. 2647–2657,
2011.
[26] L. Shi and L. Xie, “Optimal sensor power scheduling for state estimation
of Gauss–Markov systems over a packet-dropping network,” IEEE
Transactions on Signal Processing, vol. 60, no. 5, pp. 2701–2705, 2012.
Limited circulation. For review only
IEEE-TAC Submission no.: 14-0729.4
Preprint submitted to IEEE Transactions on Automatic Control. Received: February 23, 2015 00:31:54 PST
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 6
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.

