Essay on Time Value of Money and Retirement Planning

This essay explains the concept of time value of money and its importance in financial decisions. It also discusses retirement planning and investment options for accumulating funds. The essay covers topics such as discounting and compounding techniques, valuation of financial instruments, and capital budgeting decisions. The investment options for retirement planning are evaluated and compared. Course code BAO 5534 Business Finance.

BAO 5534 BUSINESS FINANCE
1

Task-1: Essay on Time Value of Money
The concept of time value of money is the basic premise of financial decisions. The
concept of time value of money confers that the value of money reduces with the efflux of time.
This means that the value of one dollar today will not be the same after 1 year from today (Drake
and Fabozzi, 2009). The purchasing power of one dollar today will reduce over the period of
time due to inflation and other economic changes. For example, a man who bought suppose one
KG bananas in one dollar today would not be able to do so after one year. After one year he
might has to pay 1.5 dollar to buy one kg bananas. The consideration of time value of money is
of utmost importance in the financial decisions. If a firm deciding on to invest in a project does
not consider the time value of money, it will end up evaluating the project’s financial viability in
wrong way (Drake and Fabozzi, 2009).
There are four basic factors which lead the consideration of time value of money concept.
These four factors are risk and uncertainty, inflation, consumption, and investment opportunity.
It is important to consider the risk and uncertainty involved in an investment decision (Silver,
2011). As the future is uncertain and hence the receipt of cash flows can not be guaranteed with
certainty, therefore, the firm makes provision for this uncertainty by adjusting the discount rate.
The inflation refers to increase in the price of goods and services over the period of one year.
The increase in the price of goods and services affects the cash flows of a firm and hence it is
important to consider inflation when assessing financial viability of the project. The discount rate
is further adjusted on account of inflation after being adjusted for risk and uncertainty (Silver,
2011).
2

Consumption and investment opportunity leads encourages a person to receive money
today rather than tomorrow. The person would always prefer to consume today rather than
consuming tomorrow. Further, the dollar money received today could be invested to earn income
for the future (Halpin and Senior, 2011). Thus, a person receiving money in future would like
have incentive or some extra charge. For example, a person receiving $100 today would not like
to defer this payment for one year if he does not receive anything greater than $100. If the person
defers the payment of $100 for one year, he would be deprived of consumption of goods or
services which he could have availed by utilizing $100 today. He would also loose opportunity to
invest money. So, he would be happy to defer it if say the payment after one year becomes $110.
In such a case, there would be some incentive to the person deferring payment for one year
(Halpin and Senior, 2011).
There are two techniques being emerged from the concept of time value of money
namely discounting and compounding. Discounting refers to bringing the value of money to be
received in future to the present times while compounding means determining the future value of
money (Baker and English, 2011). An example of discounting technique:
Value of $100 receivable after one year at discount rate of 10% would be $90.90. This is
arrived at as under:
PV = FV/(1+r)t
Here, PV = Present value
FV = Future value
R = Rate of discount
3

= 100/(1+.10)1
= 90.90
On the other hand, if we calculate let say value of $100 invested at the rate of 10% after
one year, it would amount to $110, this is called compounded value. This value has been arrived
at as under:
Fv = PV (1+r)n
= 100(1+.10)1
= $110
In capital budgeting decisions, the discounting technique is used instead of compounding.
The discounting technique provides computation of the present value of future cash flows which
is compared with the investment amount to arrive at the decision. The compounding technique in
the capital budgeting decisions can not be applied as it would be difficult to determine the rate of
return that the project would generate over the period of time. However, the future cash inflows
can be estimated with reliability. With the help of discounting technique, the present value of the
future cash flows can be determined (Shapiro, 2008).
It is to be noted that a discount rate is used in computing the present value of future cash
flows. This discount rate is determined having regards to the investor’s desired rate of return
(Shapiro, 2008). The discount rate could also be said to be the approximation to the cost of
capital of the firm. A firm may use its weighted average cost of capital as the discount rate. The
weighted average cost of capital of the firm comprises the cost of different components of the
capital such as equity, debt, and preference shares. In an all equity firm, the CAPM return could
4

also provide an approximation of the discount rate. However, whatever method is used in
computing the discount rate, a further adjustment for the risk and inflation is required. The
discount rate must incorporate risk and it should be adjusted for inflation. Further, it may be
noted that the discount rate would change from project to project because of change in the risk of
different projects (Shapiro, 2008).
There is immense use of the concept of time value of money in the valuation of the
financial instruments. All the financial instruments such as equity shares, preferences shares,
bonds and debentures are valued by discounting the future income flowing from the investment.
The equity shares are valued with reference to the discounted value of expected dividend
payments over the period (Shim and Siegel, 2008). According to the dividend discount model,
the value of an equity share can be computed by the following formula:
po = D0*(1+g)/(Ke-g)
Where,
Do = Current dividend
Ke = Cost of equity
G = growth rate
Thus, it could be observed that the value of equity shares is computed by discounting the
future dividend with the discount rate which is cost of equity in this case. The current dividend
(D0) is multiplied by the growth rate to compute the future dividend and discounting is applied
on this figure to get the value of share as on today.
5

Further, the value of bond is also computed with reference to the discounted value of the
interest payment and the discounted value of the maturity value (Shim and Siegel, 2008). The
formula used to determine the value of bond is as under:
Here, “C” refers to coupon payment, “I” is the discount rate, “m” is maturity value, and
“n” is the number of periods.
The concept of time value of money entails that the value of dollar today would not be
equal to the value of dollar tomorrow. Thus, applying this concept, the value of bond is
computed. The value of bond is equal to the sum of present value of all coupon pavements to be
made over the terms of maturity and present value of maturity value (Shim and Siegel, 2008).
The value of preference shares is also computed applying the concept of time value of
money. The value of preference share is arrived at by discounting the dividends to be received in
future and amount which would be received at the time of redemption.
Apart from the use in valuation of security, the concept of time value of money is also
used in capital budgeting decisions. Capital budgeting refers to the process of analyzing the
financial viability of long term investments (Shapiro, 2008). There are various techniques such
as net present value, payback period, internal rate of return, and profitability index which are
applied in capital budgeting decisions. The net present value technique is based on the concept of
time value of money. In this technique, the present value of cash inflows is computed with the
6

application of discount rate. The value of initial investment is deducted from the total present
value of cash inflows and result is known as net present value (Shapiro, 2008).
The discount rate is determined with reference to different parameters in different
situations. In one case, the discount rate may be determined with reference to the borrowing rate
and another it may be determined with reference to the cost of equity. Further, the discount rate
is adjusted for the risk premium and inflation effect. The higher the risk higher will be the
discount rate and higher the discount rate lower will be the present value. The discounting of
cash flows is done only after adjusting the discount rate with the risk premium and inflation
(Shapiro, 2008).
Therefore, it may be concluded from the overall discussion that the concept of time value
of money forms the basic premise of the financial management. The crucial financial
management decisions involving capital budgeting and investment decisions are based on the
concept of time value of money. The application of time value of money concept is wide spread
from valuation of securities to the investment in plant and machinery.
7

Part-2
Question-1
Studebaker is concerned about accumulating funds for his retirement. At present he is 30
years of age and he wants to accumulate funds till his retirement at the age of 60 years.
Studebaker presently has investment in the money market mutual funds. He sought advice from
the finance specialist to take out a single life insurance policy for 20 years to accumulate funds
for his retirement. Thus, the goal of Studebaker is to accumulate money for his retirement which
appears to be correct. At his retirement, the income from salary would discontinue and he would
require some source of income at that moment to finance his spending.
Question-2
Investment made 550000
Interest rate per annum 6%
Period (years) 20
Accumulated amount $1,763,924.51
The amount invested is $550,000 at the rate return of 6% per annum. Applying the
compounding technique, the value accumulated in the investment after 20 years would be
1763,925. For the purpose of compounding following equation has been used:
FV=PV*(1+r)^n
Question-3
The computation of yearly payments on the mortgage loan has been computed as below:
30 years 20 years
8

Loan amount 705000 705000
Interest rate per annum 9% 9%
Period (years) 30 20
Yearly payment $68,622.13 $77,230.26
It could be observed that the yearly payment for mortgage of $705,000 with interest rate
of 9% and time period of 30 years is $68,622.13. The yearly payment changes to $77230.26 if
the period is reduced to 20 years. The yearly payments have been computed applying the
following formula:
Question-4
The loan balance at the end of 19th and 20th year on the mortgage of $705,000 with
interest rate 9% and time of 30 years is given below:
Year
Opening
balance
Installmen
t
Interes
t
Closing
balance
19 $491,384.20 $68,622.13
44224.
6 $466,986.66
20 $466,986.66 $68,622.13
42028.
8 $440,393.33
(Appendix-1)
The closing balance of 19th year has been computed by reducing the closing balance of
18th year by the principal repaid in the 19th year. The computations for 20th year have also been
done in the similar way.
Question-5
9

Yes, it is true that $550,000 invested in the single life insurance policy would increase
accumulate to $1,763,925 in 20 years time at interest rate of 6% per annum. However, the
amount for investment in the life insurance would be arranged from the new mortgage of
$250,000 so the debt of Studebaker would increase by $250,000. The increase in debt would also
increase the yearly repayments from $42,476.82 to $68,622.13.
Question-6 (a)
The accumulated amount over the period of 20 years would be $1,398,287.14 as
computed below:
FV=PV*(1+r)^n
Investment made 300000
Interest rate per annum 8%
Period (years) 20
Accumulated amount $1,398,287.14
Question-6 (b)
The amount accumulated after 20 years on investment of 26145.31 each year at interest
rate of 8% would be as under:
10

Investment made each
year 26145.31
Interest rate per annum 8%
Period (years) 20
Accumulated amount $1,196,460.74
Question-7
The amount accumulated in 20 years time on an investment of $550,000 with a rate of
interest of 7% per annum would be as under:
FV=PV*(1+r)^n
Investment made 550000
Interest rate per annum 7%
Period (years) 20
Accumulated amount $2,128,326.45
Question-8
As per the evaluation done by Comer, the single premium life insurance policy is an
unattractive investment. The criticism of single life insurance policy done by Comer is correct.
Studebaker could earn more by investing $300,000 and a further sum of $26,145.31 each year at
the interest rate of 7%. The total amount accumulated under the single life insurance policy
would be $1,763,925 which is lower than the accumulated sum of $2,594,748 ($1,398,287+
$1,196,461).
Question-9 (a)
Studebaker will have to save $214,064.10 each year to accumulate $3,500,000 in 20
years time. The computations are shown below:
11

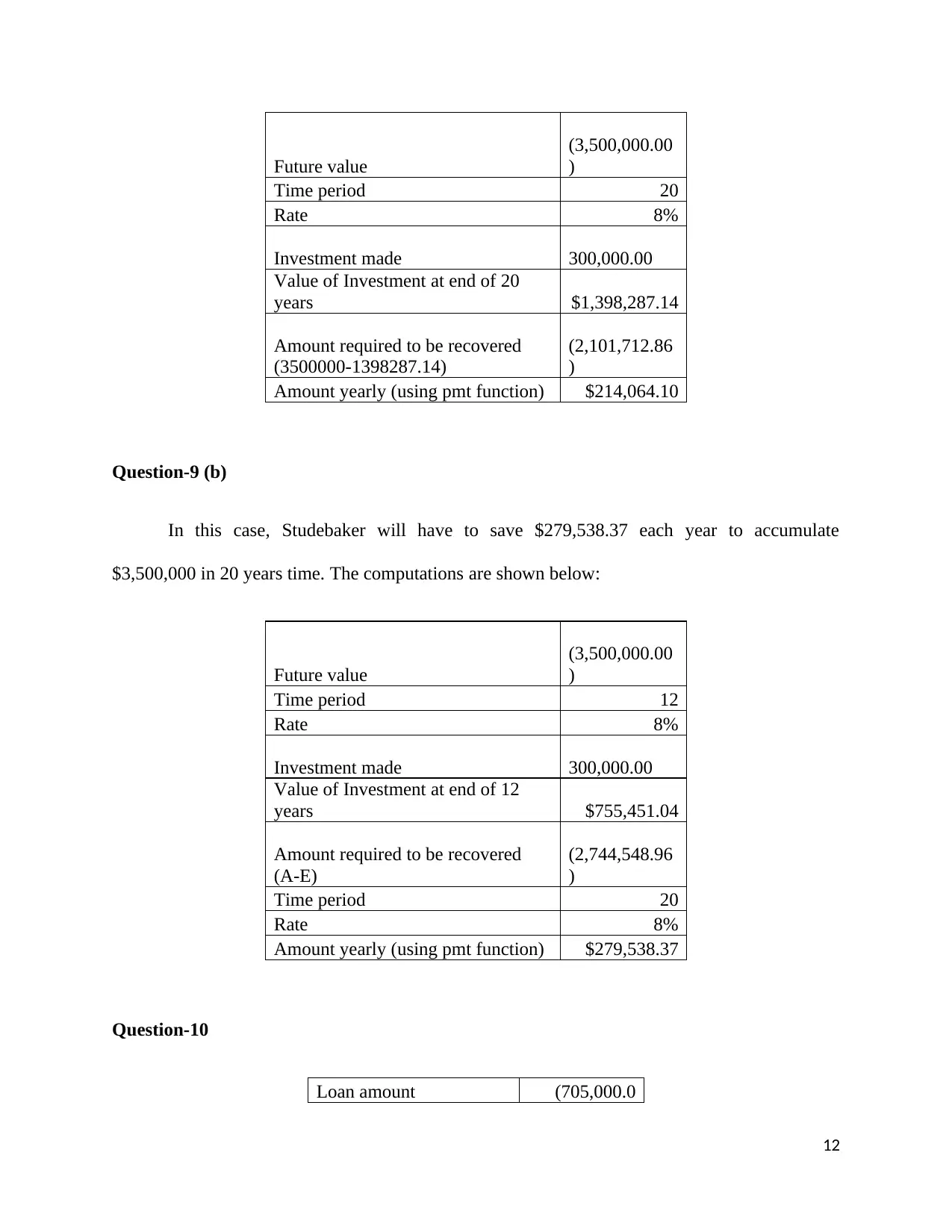
Future value
(3,500,000.00
)
Time period 20
Rate 8%
Investment made 300,000.00
Value of Investment at end of 20
years $1,398,287.14
Amount required to be recovered
(3500000-1398287.14)
(2,101,712.86
)
Amount yearly (using pmt function) $214,064.10
Question-9 (b)
In this case, Studebaker will have to save $279,538.37 each year to accumulate
$3,500,000 in 20 years time. The computations are shown below:
Future value
(3,500,000.00
)
Time period 12
Rate 8%
Investment made 300,000.00
Value of Investment at end of 12
years $755,451.04
Amount required to be recovered
(A-E)
(2,744,548.96
)
Time period 20
Rate 8%
Amount yearly (using pmt function) $279,538.37
Question-10
Loan amount (705,000.0
12

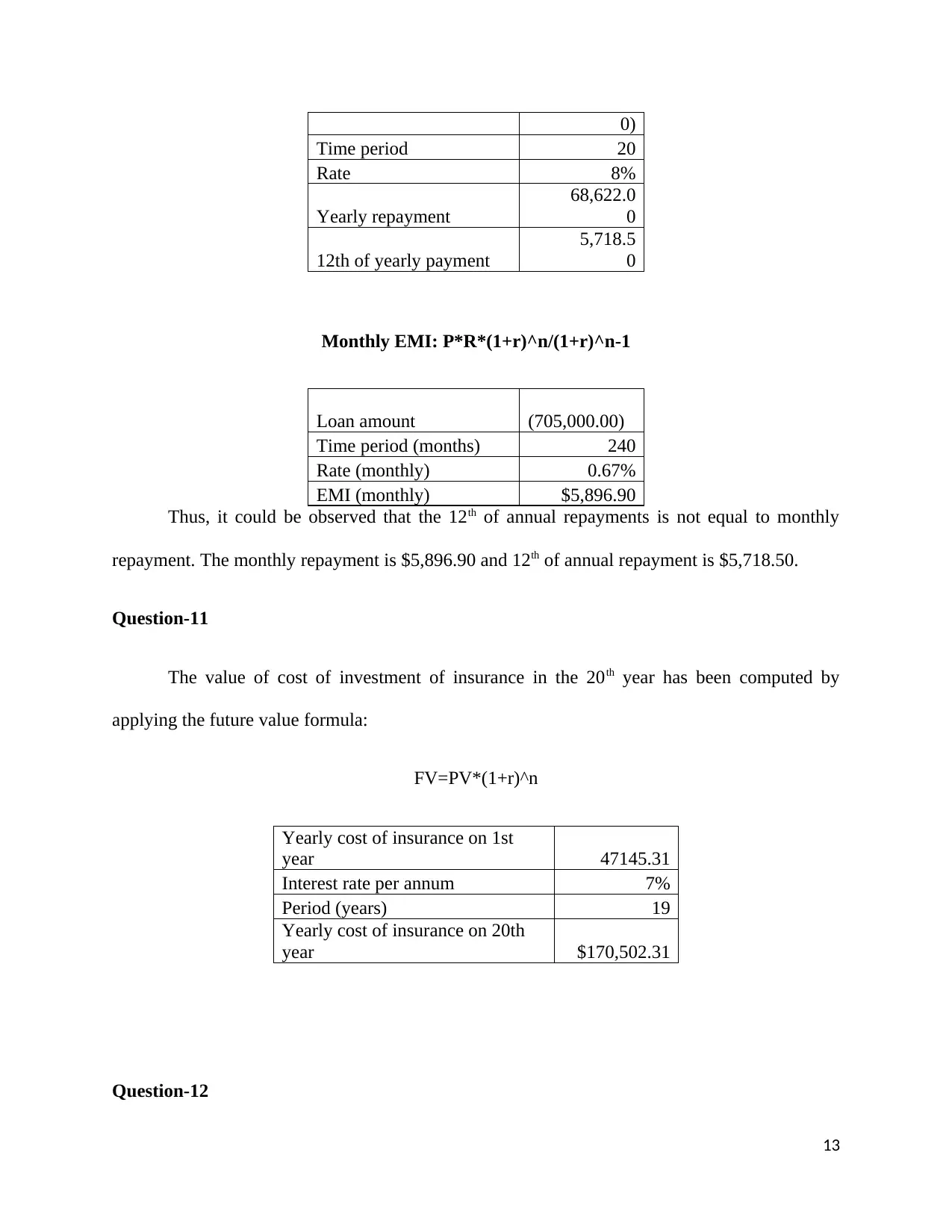
0)
Time period 20
Rate 8%
Yearly repayment
68,622.0
0
12th of yearly payment
5,718.5
0
Monthly EMI: P*R*(1+r)^n/(1+r)^n-1
Loan amount (705,000.00)
Time period (months) 240
Rate (monthly) 0.67%
EMI (monthly) $5,896.90
Thus, it could be observed that the 12th of annual repayments is not equal to monthly
repayment. The monthly repayment is $5,896.90 and 12th of annual repayment is $5,718.50.
Question-11
The value of cost of investment of insurance in the 20th year has been computed by
applying the future value formula:
FV=PV*(1+r)^n
Yearly cost of insurance on 1st
year 47145.31
Interest rate per annum 7%
Period (years) 19
Yearly cost of insurance on 20th
year $170,502.31
Question-12
13

Morton suggested Studebaker making investment in a single life insurance policy to
accumulate the funds for retirement. For this purpose, he suggested to take out a mortgage of
$250,000 and invest the amount along with a sum of $300,000 held in the mutual funds. Thus, he
suggested taking out a life insurance policy for $550,000 which would accumulate a sum of
$1,763,925 over the period of 20 years. However, the strategy suggested by Morton is not
financial beneficial for Studebaker. The cost of mortgage at 9% would increase the expenses
more than the income accrued on the life insurance policy.
Question-13
The proposed investment plan involves taking out a mortgage for $250,000 and investing
in a single life insurance policy for a sum of $550,000, a sum of $300,000 of which could be
arranged by liquidating the investment in mutual funds. The investment plan shown by Morton
indicates that it would be beneficial for Studebaker to take out the life insurance policy. But the
actually it ignores the opportunity cost, certain out of pocket expenses, and taxes. When the
opportunity cost, out of pocket expenses, and taxes are considered, the investment in life
insurance policy would not be beneficial. It is clear from the answer to question-6 above that
Studebaker can accumulate a sum of $2,594,748 by simply investing the money available at 8%
interest. The accumulated amount on the life insurance policy would be $1,763,925 which is less
than what Studebaker could accumulate otherwise. Hence, the proposed investment plan is not
financial beneficial to Studebaker.
References
14

Baker, H.K. and English, P. 2011. Capital Budgeting Valuation: Financial Analysis for Today's
Investment Projects. John Wiley & Sons.
Drake, P.P. and Fabozzi, F.J. 2009. Foundations and Applications of the Time Value of Money.
John Wiley & Sons.
Halpin, D.W. and Senior, B.A. 2011. Financial Management and Accounting Fundamentals for
Construction. John Wiley & Sons.
Shapiro. 2008. Capital Budgeting And Investment Analysis. Pearson Education India.
Shim, J.K. and Siegel, J.G. 2008. Financial Management. Barron's Educational Series.
Silver, T.L. 2011. The Time Value of Life: Why Time Is More Valuable Than Money. iUniverse.
Appendix-1
15

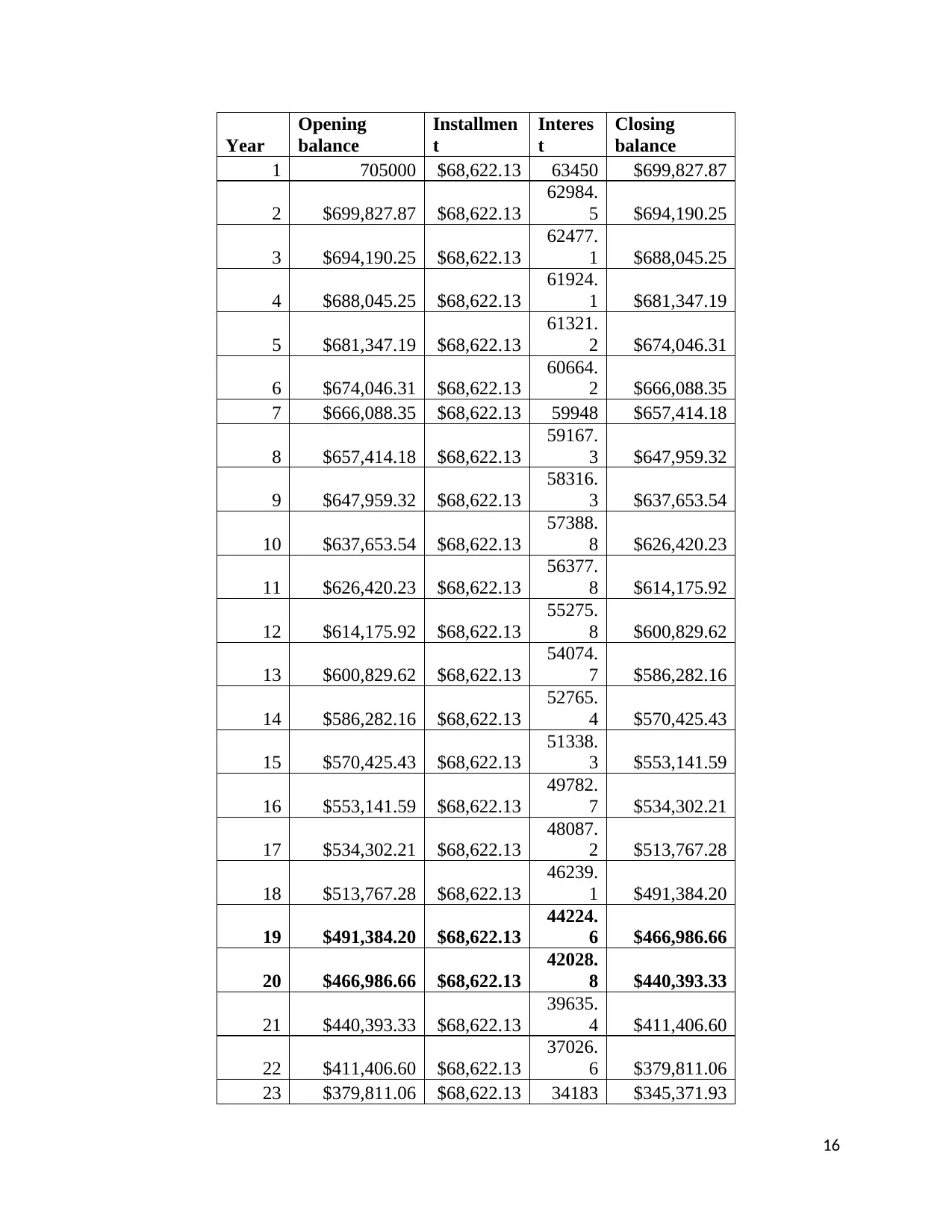
Year
Opening
balance
Installmen
t
Interes
t
Closing
balance
1 705000 $68,622.13 63450 $699,827.87
2 $699,827.87 $68,622.13
62984.
5 $694,190.25
3 $694,190.25 $68,622.13
62477.
1 $688,045.25
4 $688,045.25 $68,622.13
61924.
1 $681,347.19
5 $681,347.19 $68,622.13
61321.
2 $674,046.31
6 $674,046.31 $68,622.13
60664.
2 $666,088.35
7 $666,088.35 $68,622.13 59948 $657,414.18
8 $657,414.18 $68,622.13
59167.
3 $647,959.32
9 $647,959.32 $68,622.13
58316.
3 $637,653.54
10 $637,653.54 $68,622.13
57388.
8 $626,420.23
11 $626,420.23 $68,622.13
56377.
8 $614,175.92
12 $614,175.92 $68,622.13
55275.
8 $600,829.62
13 $600,829.62 $68,622.13
54074.
7 $586,282.16
14 $586,282.16 $68,622.13
52765.
4 $570,425.43
15 $570,425.43 $68,622.13
51338.
3 $553,141.59
16 $553,141.59 $68,622.13
49782.
7 $534,302.21
17 $534,302.21 $68,622.13
48087.
2 $513,767.28
18 $513,767.28 $68,622.13
46239.
1 $491,384.20
19 $491,384.20 $68,622.13
44224.
6 $466,986.66
20 $466,986.66 $68,622.13
42028.
8 $440,393.33
21 $440,393.33 $68,622.13
39635.
4 $411,406.60
22 $411,406.60 $68,622.13
37026.
6 $379,811.06
23 $379,811.06 $68,622.13 34183 $345,371.93
16

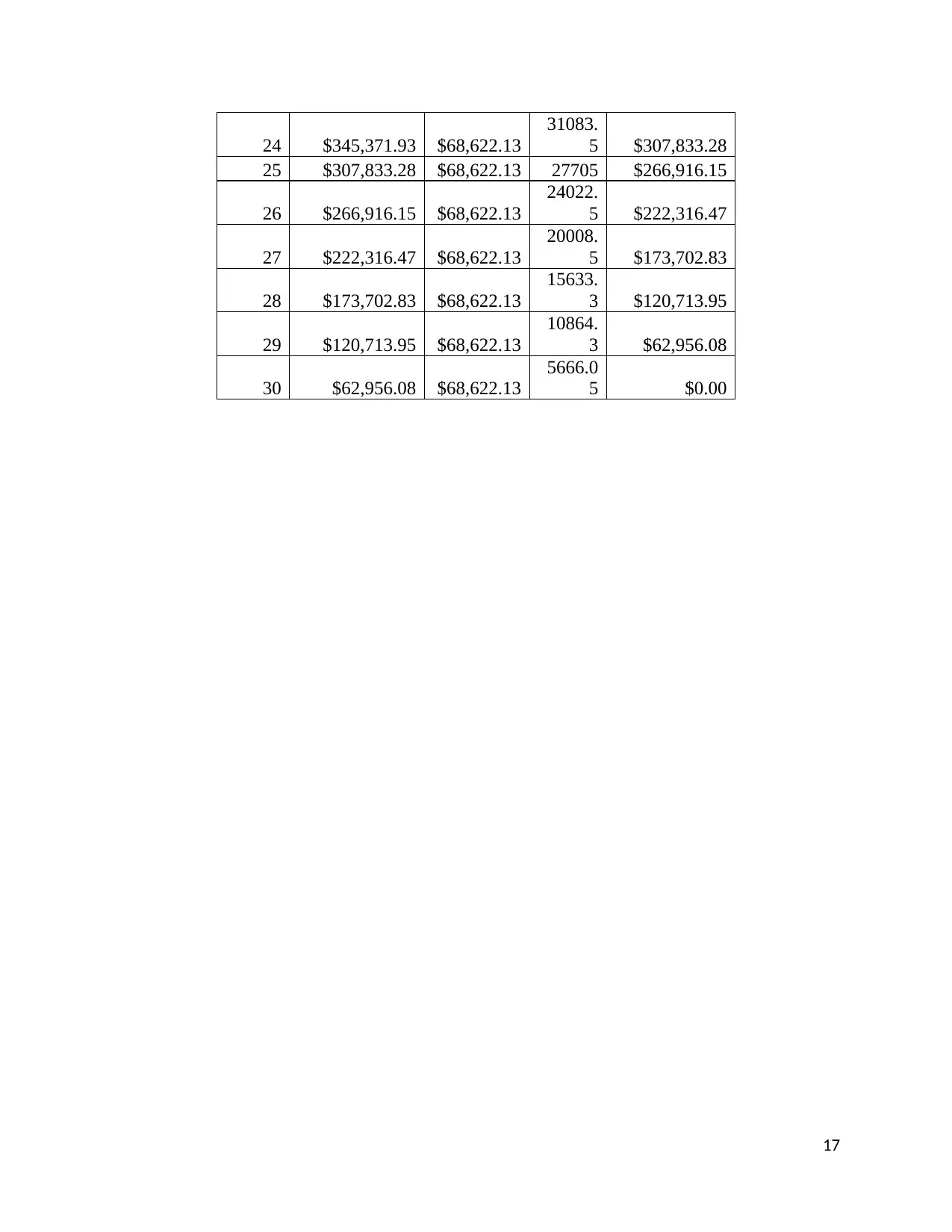
24 $345,371.93 $68,622.13
31083.
5 $307,833.28
25 $307,833.28 $68,622.13 27705 $266,916.15
26 $266,916.15 $68,622.13
24022.
5 $222,316.47
27 $222,316.47 $68,622.13
20008.
5 $173,702.83
28 $173,702.83 $68,622.13
15633.
3 $120,713.95
29 $120,713.95 $68,622.13
10864.
3 $62,956.08
30 $62,956.08 $68,622.13
5666.0
5 $0.00
17