Testing Distribution of Duration of Symptoms of Drug

This article discusses the testing of the distribution of the duration of symptoms of drug 1 and drug 2 for malaria patients. It includes histograms, confidence interval estimates, and hypothesis testing using t-test.

Title:
Assignment Name:
Student Name:
Course Name and Number:
Professor:
Date:

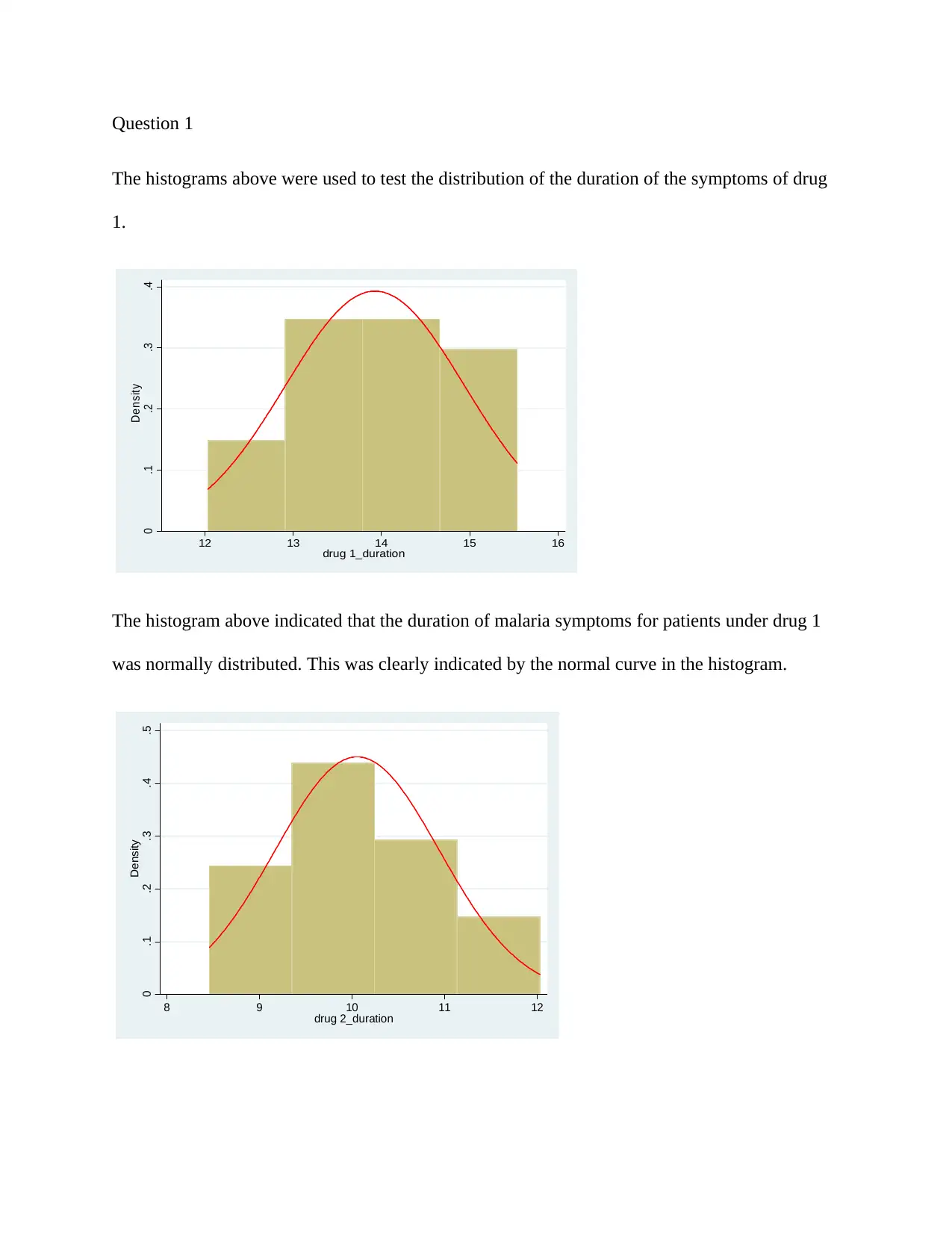
Question 1
The histograms above were used to test the distribution of the duration of the symptoms of drug
1.
0 .1 .2 .3 .4
Density
12 13 14 15 16
drug 1_duration
The histogram above indicated that the duration of malaria symptoms for patients under drug 1
was normally distributed. This was clearly indicated by the normal curve in the histogram.
0 .1 .2 .3 .4 .5
Density
8 9 10 11 12
drug 2_duration

The histogram above indicated that the duration of malaria symptoms for patients under drug 2
was normally distributed. However, it was positively skewed as the normal curve indicated.
Since both the duration of malaria symptoms of drug1 and drug2 this meant that their confidence
interval could be estimated using the standard normal distribution (Selbæk and Engedal, 2012).
The following table represents the mean and the 95% corresponding confidence interval.
Mean Lower 95% confidence
interval
Upper 95% confidence
interval
13.9 13.5 14.4
The above table represents the 95% confidence interval estimates for the mean duration of the
symptoms of drug 1.
Mean Lower 95% confidence
interval
Upper 95% confidence
interval
10.1 9.7 10.4
The above table represents the 95% confidence interval estimate for the mean duration of the
symptoms of drug2.
Question 2
The confidence interval has the interpretation that the probability that the true mean of the
duration of symptoms of drug1 and drug2 will belong in the interval, there is 95% certainty (Lee,
2016).

Question 3
Since the number of observations was less than thirty (i.e. n<30) an independent sample t-test
was used to compare whether there was a difference in the mean duration of drug1 and drug2.
This is because the duration of drug 1 and drug 2 do not depend on each other and therefore they
are independent.
The following hypothesis was formulated:
H0: there is no difference in the mean duration of the two drugs
Versus
H1: there is a difference in the mean duration of the two drugs.
The test was carried out at 5% level of significance. The T statistics was used to test the
hypothesis above, and below is the output of the test.
Two-sample t test with equal variances
Variable Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
drug1_~n 23 13.9 .2 1.0 13.5 14.4
drug2_~n 23 10.0 .2 .9 9.7 10.4
combined 46 12.0 .3 2.27 11.3 12.6
diff 3.9 .3 3.3 4.4

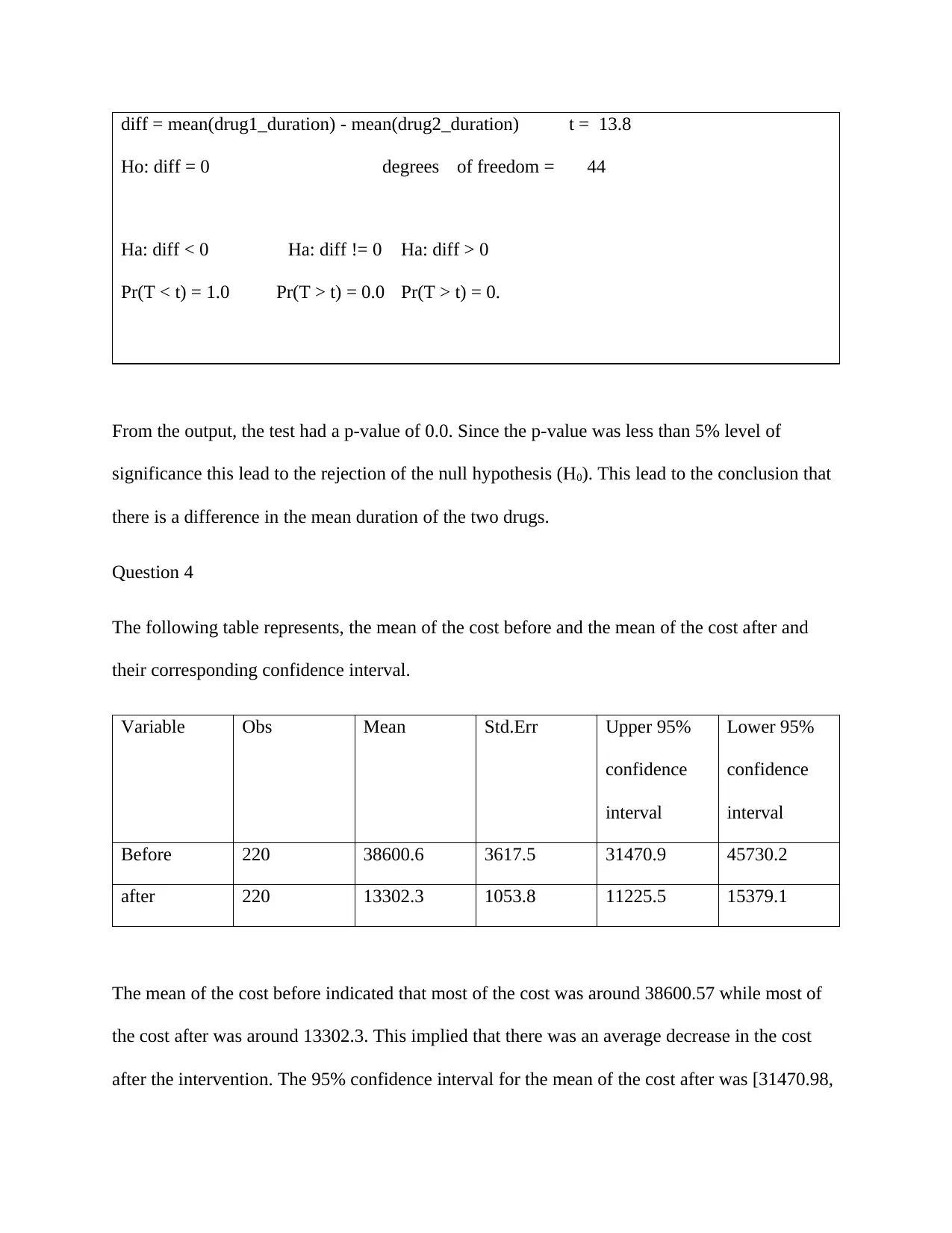
diff = mean(drug1_duration) - mean(drug2_duration) t = 13.8
Ho: diff = 0 degrees of freedom = 44
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 1.0 Pr(T > t) = 0.0 Pr(T > t) = 0.
From the output, the test had a p-value of 0.0. Since the p-value was less than 5% level of
significance this lead to the rejection of the null hypothesis (H0). This lead to the conclusion that
there is a difference in the mean duration of the two drugs.
Question 4
The following table represents, the mean of the cost before and the mean of the cost after and
their corresponding confidence interval.
Variable Obs Mean Std.Err Upper 95%
confidence
interval
Lower 95%
confidence
interval
Before 220 38600.6 3617.5 31470.9 45730.2
after 220 13302.3 1053.8 11225.5 15379.1
The mean of the cost before indicated that most of the cost was around 38600.57 while most of
the cost after was around 13302.3. This implied that there was an average decrease in the cost
after the intervention. The 95% confidence interval for the mean of the cost after was [31470.98,

45730.17]. The confidence interval indicated that there was 95% certainty that the true mean of
the cost before would lie within the interval. The 95% confidence interval for the mean of the
cost after was [11225.46, 15379.14]. The confidence interval indicated that there was 95%
certainty that the true mean of the cost before would lie within the interval (Hopkins, 2017).
Testing the null hypothesis that there was no need for intervention (the difference before and
after intervention of a new drug is zero) the 95% confidence interval was used to make the
decision. Since the null value was not included in the confidence interval (i.e. the difference
before and after intervention is zero) the null hypothesis was rejected and thus the conclusion
was the intervention of new drug changed the average hospitalization cost.
The following hypothesis was used to investigate whether there was a need for intervention.
H0: intervention was insignificant
Versus
H1: intervention was significant.
Since the null value was not included in the confidence interval (i.e. μ=0) the null hypothesis
was rejected. Therefore, the intervention of the new drug was significant.
Question 5
The following output represents the proportion of those who were vaccinated and those who
were not vaccinated.
Vaccination Proportion Std.Err Lower 95%
confidence
interval
Upper 95%
confidence
interval

Received free
vaccination
0.51 0.02 0.48 0.5
The output indicated that the proportion of children who received free vaccination was 0.51.
The 95% confidence interval for the proportion of children who were vaccinated was [0.48,
0.54].
The probability distribution used is a normal distribution. This is because the proportions are
used like sample estimates of the means that follows a normal distribution (Morey et al, 2016).
References
Hopkins, W.G., 2017. A Spreadsheet for Deriving a Confidence Interval, Mechanistic Inference
and Clinical Inference from a P Value. Sportscience, 21.
Lee, D.K., 2016. Alternatives to P value: confidence interval and effect size. Korean journal of
anesthesiology, 69(6), p.555.
Morey, R.D., Hoekstra, R., Rouder, J.N., Lee, M.D. and Wagenmakers, E.J., 2016. The fallacy
of placing confidence in confidence intervals. Psychonomic bulletin & review, 23(1), pp.103-
123.
Selbæk, G. and Engedal, K., 2012. Stability of the factor structure of the Neuropsychiatric
Inventory in a 31-month follow-up study of a large sample of nursing-home patients with
dementia. International Psychogeriatrics, 24(1), pp.62-73.