Themes of Tone and Sense of Belonging in Speech: Importance of Tone and Culture

The speaker discusses the impact of tone on the meaning of words and emphasizes the importance of identifying the right tone to pass the correct information. She also highlights the significance of staying true to one's culture and background, and the sense of belonging it brings. The speech touches on the themes of tone and sense of belonging.

Data set one
The video transcript presents speaker’s thoughts and concerns about the significance of tone and
mood of speech. Out of the video transcript, two themes emerge, the theme on tone and the
theme on sense of belonging;
Theme number Theme Name
1 Tone
2 Sense of belonging
Tone
Tone refers to the use of pitch of sound to distinguish grammatical or lexical meaning of words
and phrases. Presentations catch group of people attention and draw the audience into the subject
of the under speech, yet they likewise set the tone for the general discourse. Presentations
(Beattie, 2007). Right tone ensures that right information is passed during any address.
The theme of tone presents itself by the speaker describing the influence of tone on meaning of
words using the example of the phrase “You don’t belong here.” Depending on the tone used for
the phrase, he following three meanings can be deduced.
i. There is no function or role for the person recipient of the phrase.
ii. The recipient of the phrase is too queer to handle.
iii. There is no way for recipient of the phrase to exist or be happy in the situation under
discussion.
These three instances demonstrate that tone has a significant impact on meanings of words and
phrases (Vinay, 2015). The right tone should thereby be identified in order to pass the correct
information.
She goes further to emphasize the fact of tone.

“What she was referring to was the fact that I could switch off the twang and slip into a native
tongue, and so I chose to let her in on a few other things which locate me as a Motswana, not just
by virtue of the fact that I speak a language or I have family there, but that a rural child lives
within this shiny visage of fabulosity.”
Sense of belonging
The theme of a sense of belonging clearly emerges from the speaker’s address.
She states that she could easily change the twang from one language to another. Based on the
language in context, she can easily change her tone to bring out words clearly in specific
languages. Based on her phone conversation with her mother, she could easily and perfectly
speak in her mother tongue.
The speaker brings out the essence of belonging to one’s roots and background. Being educated
cannot erase one’s history or background. She says;
“A rural child lives within this shiny visage of fabulosity.”
She emphasizes on the point of being real to their culture, history and background. Sense of
belonging to one’s roots enhances meaning in life (Lambert, 2013).
In a poetic, individual talk, TED Fellow Katlego Kolanyane-Kesupile looks at the association
between her advanced strange way of life and her youth childhood in a provincial town in
Botswana. "In a time where being brown, queer, African and seen as worthy of space means
being everything but rural, I fear that we're erasing the very struggles that got us to where we are
now," she says. "Indigenizing my queerness means bridging the many exceptional parts of
myself."

Data set two
The two data sets are unrelated, are not normally distributed and of small sample sizes, therefore
we use a non-parametric independent samples test. A non-parametric test that tests differences in
two independent samples is the Mann Whitney U test. For this case of this study, Mann Whitney
U test will be used for testing whether or not the means of the experimental and control groups
are equal. The following steps are employed for the analysis.
Step 1: Hypothesis
The null and alternative hypotheses for the analysis are;
H0: There is no difference in the means of the experimental and control groups.
H1: There is a difference in the means of the experimental and control groups.
Step 2: We determine whether the hypothesis under test is either one-sided or two-sided.
Step 3: We specify the level of significance, alpha for our test. For our case under investigation,
the hypothesis is two tailed as it tests whether there is a difference between means of the two
groups.
Step 4: Using SPSS we perform the Mann Whiney U test or independence of groups.
Step 5: We make inference based on the results of the Mann Whitney test.
Ranks
Group N Mean Rank Sum of Ranks
Differences Experimental 16 11.59 185.50
Control 18 22.75 409.50
Total 34
Test Statisticsa
Differences

Mann-Whitney U 49.500
Wilcoxon W 185.500
Z -3.270
Asymp. Sig. (2-tailed) .001
Exact Sig. [2*(1-tailed Sig.)] .001b
a. Grouping Variable: Group
b. Not corrected for ties.
The p-value of 0.001 indicates a probability of 1 in 1,000: if the populations of experimental and
control groups are similar, then we've a 1 in 1,000 chance of finding the large difference we
observe in our sample. However, the means of the experimental and control groups cannot be
similar.
Results are analyzed at the 5% level of significance. The p-value equals 0.001 which is less than
0.05 (the alpha value). The small p-value indicates that we reject the null hypothesis that there is
no difference in the means of the experimental (means are equal) and control groups in favor of
the alternative hypothesis that there is a difference in the means of the experimental and control
groups (means are not equal).
We therefore conclude that there is indeed a difference in means between the experimental and
the control groups. We have statistically significant evidence at α =0.05 to show that the people
who watched a clip about the dangers of driving over the speed limit and people who watched a
clip about gardening are not equal on opinions about what a safe speed is on a country lane.

Data set 3
The two data sets are independent; therefore, we use a chi-square test. For this case of this study,
chi-square test will be used for testing whether or not there is a difference in the manner in which
males and females visited the washroom in a busy restaurant. The Chi-Square test of association
is utilized to decide whether there is a critical connection between two nominal factors. The
recurrence of every class for one nominal variable is looked at over the classifications of the
second nominal variable. The information can be shown in a possibility table where each line
speaks to a classification for one factor and every section speaks to a classification for the other
variable. The Chi square test of independence examines relationship between independent
variables. The null hypothesis is that there exists no relationship between variables whereas the
alternative hypothesis tests that there is an association between variables.
The following steps are employed for the analysis.
Step 1: Hypothesis
The null and alternative hypotheses for the analysis are;
H0: There is no difference on whether people visit the washroom individually or in groups for
males and females.
H1: There is a difference on whether people visit the washroom individually or in groups for
males and females.
Step 2: We determine whether the hypothesis under test is either one-sided or two-sided.
Step 3: We specify the level of significance, alpha for our test. For our case under investigation,
the hypothesis is two tailed as it tests whether there is a difference on whether people visit the
washroom individually or in groups for males and females.
Step 4: Using SPSS we perform the chi-square test or independence of groups.

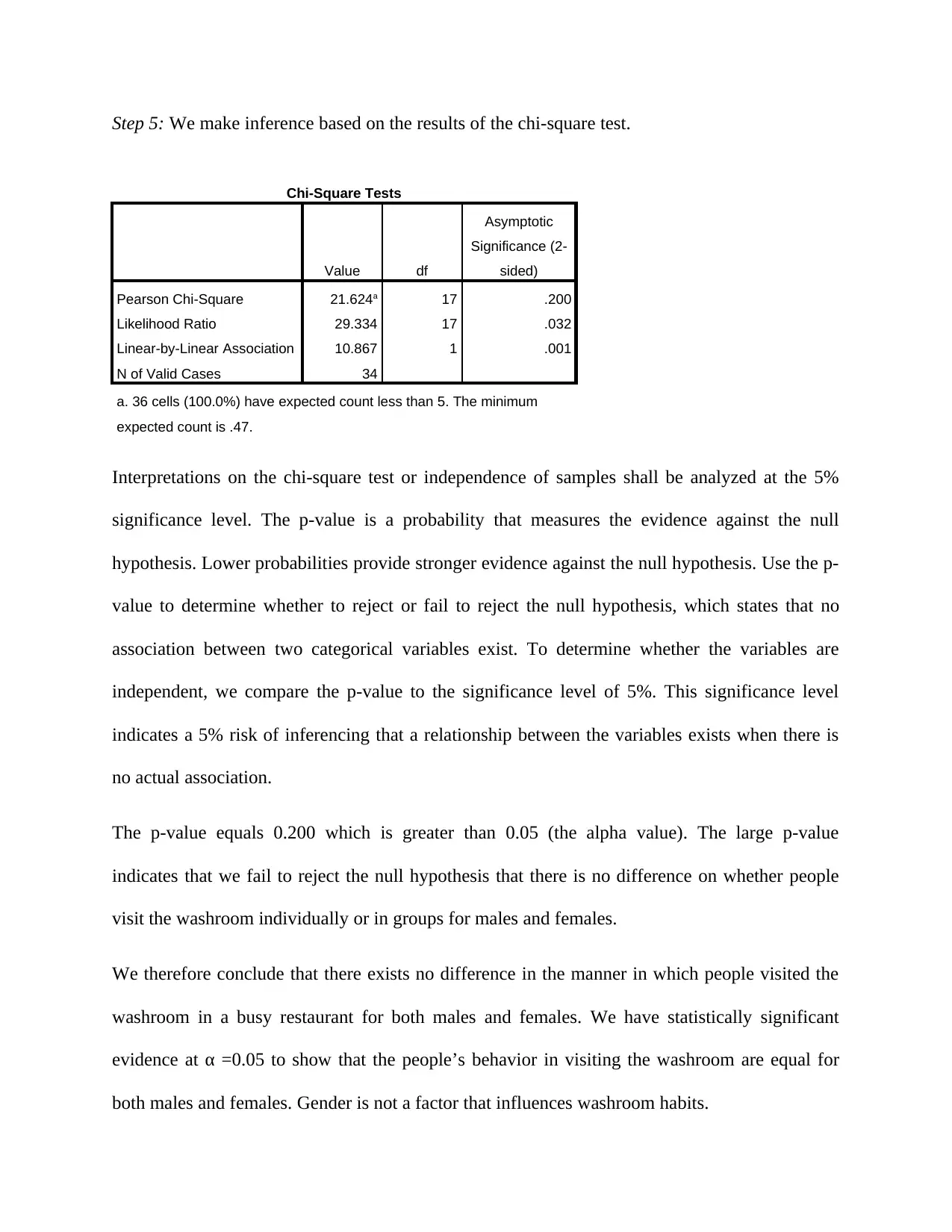
Step 5: We make inference based on the results of the chi-square test.
Chi-Square Tests
Value df
Asymptotic
Significance (2-
sided)
Pearson Chi-Square 21.624a 17 .200
Likelihood Ratio 29.334 17 .032
Linear-by-Linear Association 10.867 1 .001
N of Valid Cases 34
a. 36 cells (100.0%) have expected count less than 5. The minimum
expected count is .47.
Interpretations on the chi-square test or independence of samples shall be analyzed at the 5%
significance level. The p-value is a probability that measures the evidence against the null
hypothesis. Lower probabilities provide stronger evidence against the null hypothesis. Use the p-
value to determine whether to reject or fail to reject the null hypothesis, which states that no
association between two categorical variables exist. To determine whether the variables are
independent, we compare the p-value to the significance level of 5%. This significance level
indicates a 5% risk of inferencing that a relationship between the variables exists when there is
no actual association.
The p-value equals 0.200 which is greater than 0.05 (the alpha value). The large p-value
indicates that we fail to reject the null hypothesis that there is no difference on whether people
visit the washroom individually or in groups for males and females.
We therefore conclude that there exists no difference in the manner in which people visited the
washroom in a busy restaurant for both males and females. We have statistically significant
evidence at α =0.05 to show that the people’s behavior in visiting the washroom are equal for
both males and females. Gender is not a factor that influences washroom habits.

Data set 4
Since the two trial types, tourist locations and snakes are independent, we perform an
independent samples t-test or equality of means. The Independent Samples t-test is a parametric
test that compares the means of two independent groups in order to determine whether there is
statistical evidence that the associated population means are significantly different.
We proceed as follows:
Step 1: Hypothesis
H0: Changes in the snake images would not be quicker to detect compared to changes in the
tourist location images.
H1: Changes in the snake images would be quicker to detect compared to changes in the tourist
location images.
Step 2: We determine whether the hypothesis is one or two-tailed. Our hypothesis is two tailed.
Step 3: Results shall be analyzed at the 5% level of significance.
Step 4: Using SPSS we perform the independent samples t test.
Step 5: Based on results, we draw inference about the hypothesis.
Independent Samples Test
Levene's Test for
Equality of Variances t-test for Equality of Means
F Sig. t df
Sig. (2-
tailed)
Mean
Differenc
e
Std. Error
Differenc
e
95% Confidence
Interval of the
Difference
Lower Upper

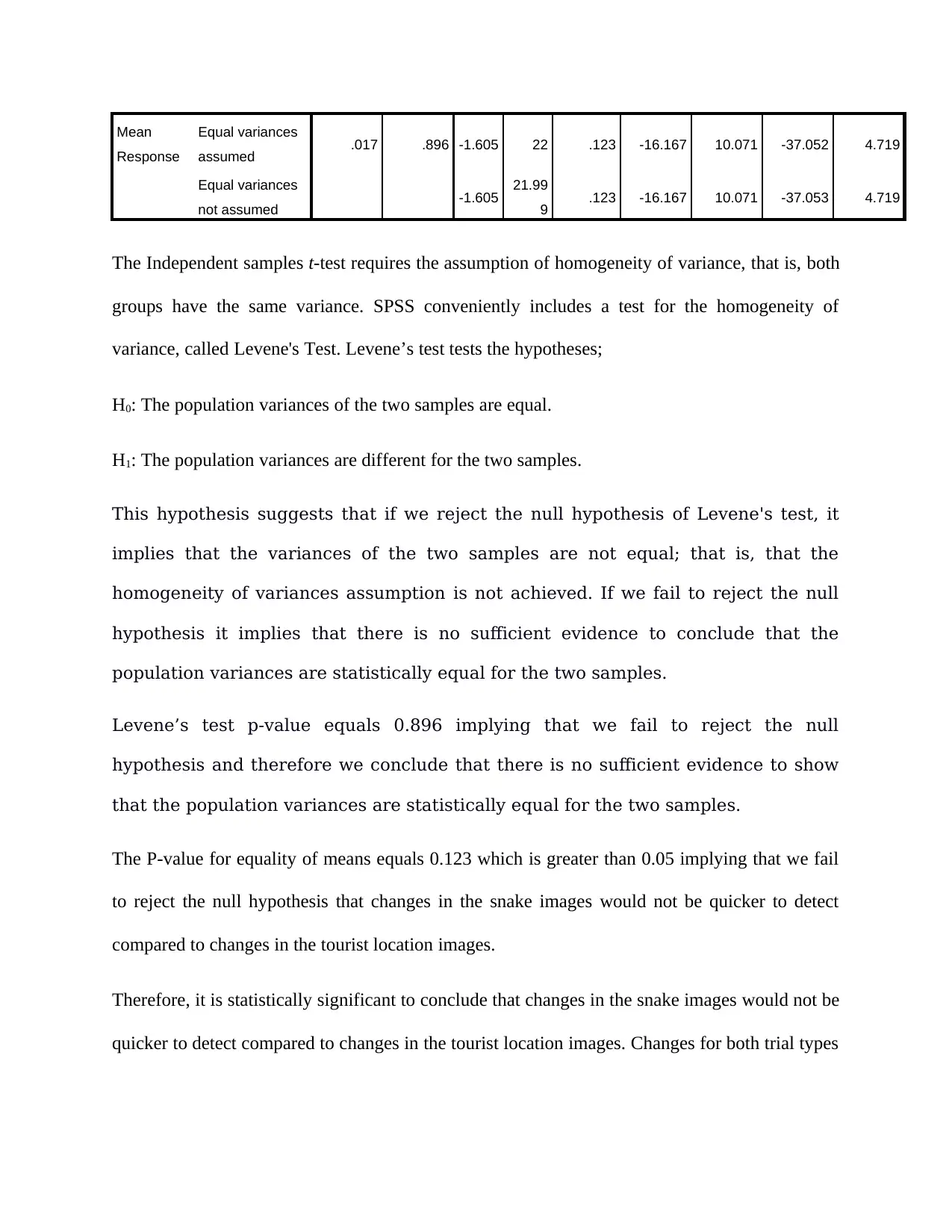
Mean
Response
Equal variances
assumed .017 .896 -1.605 22 .123 -16.167 10.071 -37.052 4.719
Equal variances
not assumed -1.605 21.99
9 .123 -16.167 10.071 -37.053 4.719
The Independent samples t-test requires the assumption of homogeneity of variance, that is, both
groups have the same variance. SPSS conveniently includes a test for the homogeneity of
variance, called Levene's Test. Levene’s test tests the hypotheses;
H0: The population variances of the two samples are equal.
H1: The population variances are different for the two samples.
This hypothesis suggests that if we reject the null hypothesis of Levene's test, it
implies that the variances of the two samples are not equal; that is, that the
homogeneity of variances assumption is not achieved. If we fail to reject the null
hypothesis it implies that there is no sufficient evidence to conclude that the
population variances are statistically equal for the two samples.
Levene’s test p-value equals 0.896 implying that we fail to reject the null
hypothesis and therefore we conclude that there is no sufficient evidence to show
that the population variances are statistically equal for the two samples.
The P-value for equality of means equals 0.123 which is greater than 0.05 implying that we fail
to reject the null hypothesis that changes in the snake images would not be quicker to detect
compared to changes in the tourist location images.
Therefore, it is statistically significant to conclude that changes in the snake images would not be
quicker to detect compared to changes in the tourist location images. Changes for both trial types

could either be equal or could detected less quickly for the snake images than for the tourist
location images.
Data set 5
One-way ANOVA is carried out to determine equality of means for the independent samples.
The hypothesis tests whether or not the means of the three samples are equal. Analysis of
Variance tests general differences rather than specific differences.
Step 1: Hypothesis
H0: There is no difference in the means of ratings of neutral items paired with positive stimuli,
ratings of neutral items paired with negative stimuli and ratings of neutral items paired with
neutral stimuli.
H1: At least one of the means of the samples is different for ratings of neutral items paired with
positive stimuli, ratings of neutral items paired with negative stimuli and ratings of neutral items
paired with neutral stimuli.
Step 2: We determine whether the hypothesis under test is either one-sided or two-sided.
Step 3: We specify the level of significance, alpha for our test. For our case under investigation,
the hypothesis is two tailed as it tests whether or not the means of the samples are different for
ratings of neutral items paired with positive stimuli, ratings of neutral items paired with negative
stimuli and ratings of neutral items paired with neutral stimuli.
Step 4: Using SPSS we perform the ANOVA test or independence of groups.
Step 5: We make inference based on the results of the ANOVA test.
ANOVA
Scores

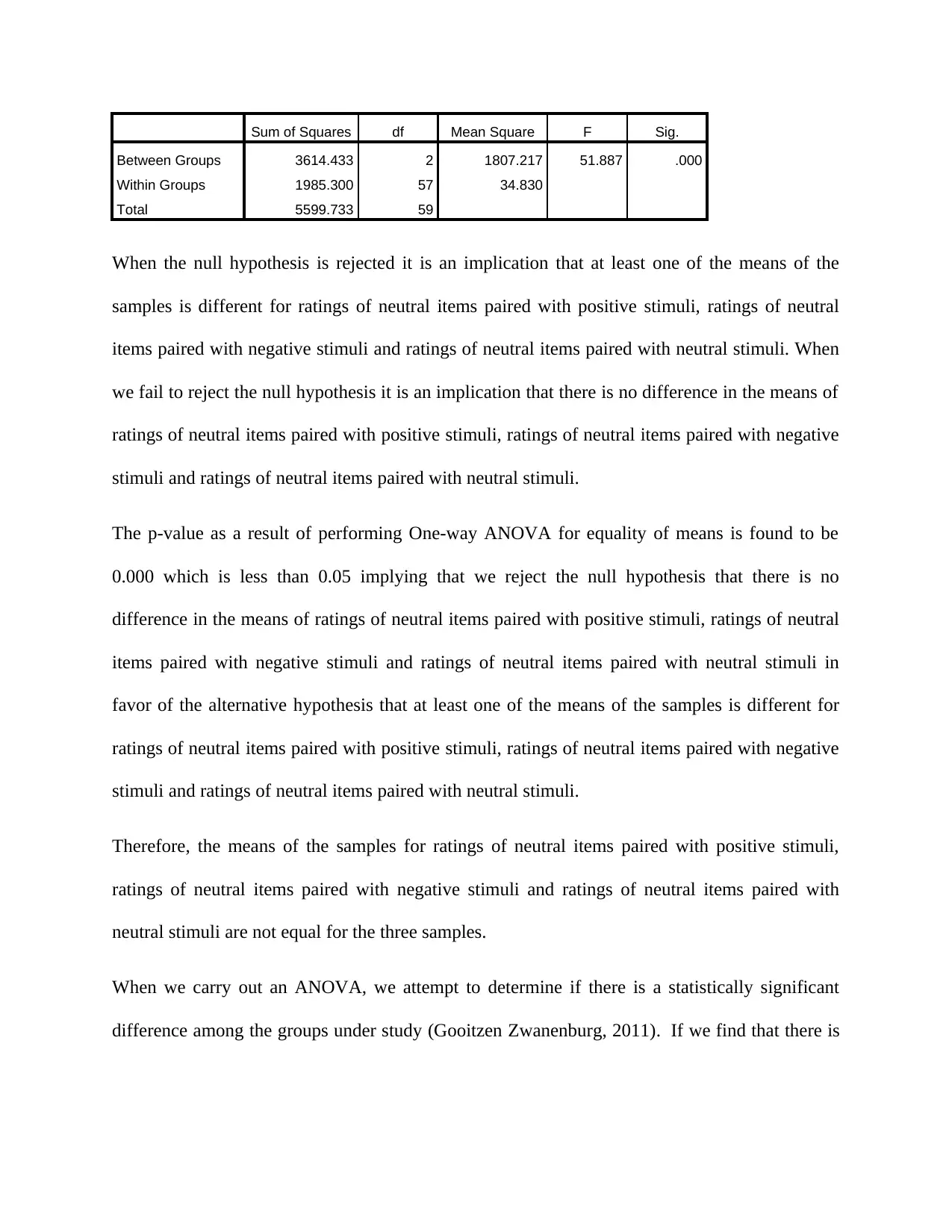
Sum of Squares df Mean Square F Sig.
Between Groups 3614.433 2 1807.217 51.887 .000
Within Groups 1985.300 57 34.830
Total 5599.733 59
When the null hypothesis is rejected it is an implication that at least one of the means of the
samples is different for ratings of neutral items paired with positive stimuli, ratings of neutral
items paired with negative stimuli and ratings of neutral items paired with neutral stimuli. When
we fail to reject the null hypothesis it is an implication that there is no difference in the means of
ratings of neutral items paired with positive stimuli, ratings of neutral items paired with negative
stimuli and ratings of neutral items paired with neutral stimuli.
The p-value as a result of performing One-way ANOVA for equality of means is found to be
0.000 which is less than 0.05 implying that we reject the null hypothesis that there is no
difference in the means of ratings of neutral items paired with positive stimuli, ratings of neutral
items paired with negative stimuli and ratings of neutral items paired with neutral stimuli in
favor of the alternative hypothesis that at least one of the means of the samples is different for
ratings of neutral items paired with positive stimuli, ratings of neutral items paired with negative
stimuli and ratings of neutral items paired with neutral stimuli.
Therefore, the means of the samples for ratings of neutral items paired with positive stimuli,
ratings of neutral items paired with negative stimuli and ratings of neutral items paired with
neutral stimuli are not equal for the three samples.
When we carry out an ANOVA, we attempt to determine if there is a statistically significant
difference among the groups under study (Gooitzen Zwanenburg, 2011). If we find that there is

a difference, we will then need to examine where the group differences are found. At this point
we could run post-hoc tests which are t tests examining mean differences between the groups.
Data set 6
Pearson correlation analysis is carried out to assess the relationship between IQ and SES.
Correlation is a statistical technique that investigates association between variables (Harnly,
2014). Correlation can be negative or positive. Negative correlation implies a negative
relationship between variables under investigation while positive correlation implies a positive
association between variables. Strength of correlation could be weakly positive, weakly negative,
strongly positive or strongly negative.
Step 1: Hypothesis
The hypotheses that the test shall try to assess is;
H0: IQ and SES do not have a positive relationship.
H1: IQ and SES have a positive relationship.
Step 2: We determine whether the hypothesis under test is either one-sided or two-sided.
Step 3: We specify the level of significance, alpha for our test. For our case under investigation,
the hypothesis is two tailed as it tests whether or not IQ and SES have a positive relationship.
Step 4: Using SPSS we perform the correlation analysis.
Step 5: We make inference based on the results of the correlation analysis test.
Correlations
IQ SES

IQ Pearson Correlation 1 .462*
Sig. (2-tailed) .013
N 28 28
SES Pearson Correlation .462* 1
Sig. (2-tailed) .013
N 28 28
*. Correlation is significant at the 0.05 level (2-tailed).
The Pearson correlation coefficient, r was found to be 0.462 implying a positive relationship
between IQ and SES. P-value (0.013) being less than 0.05 implies a rejection of the null
hypothesis that IQ and SES do not have a positive relationship in favor of the alternative
hypothesis that IQ and SES have a positive relationship (BRADLEY R. ENTNER WRIGHT,
2009).
The results show that IQ is positively associated with SES, implying that an increase in IQ scores
result to a corresponding increase in SES scores, and an increase in SES scores result to a
corresponding increase in IQ scores. Likewise, a decrease in IQ scores result to a decrease in
SES scores and correspondingly, a decrease in SES scores results to a decrease in IQ scores
(Calabrese Generosa, 2016).

References
Beattie, R. C. (2007). Effects of Rise-Fall Time and Repetition Rate on the Auditory Brainstem Response
to 0.5 and 1 kHz Tone Bursts Using Normal-Hearing and Hearing-Impaired Subjects.
Scandinavian Audiology, 18.
BRADLEY R. ENTNER WRIGHT, A. C. (2009). RECONSIDERING THE RELATIONSHIP BETWEEN SES AND
DELINQUENCY: CAUSATION BUT NOT CORRELATION. 11.
Calabrese Generosa, A. O. (2016). Li The correlation between FDI and knowledge transfer, and their
effect on domestic innovation: Evidence from China. 9.
Gooitzen Zwanenburg, H. C. (2011). ANOVA–principal component analysis and ANOVA–simultaneous
component analysis: a comparison. 3.
Harnly, J. M. (2014). Characterization of Near-Infrared Spectral Variance in the Authentication of Skim
and Nonfat Dry Milk Powder Collection Using ANOVA-PCA, correlation, and Partial Least-Squares
Regression. Journal of Agricultural and Food Chemistry, 8.
Lambert, N. M. (2013). Sense of Belonging Enhances Meaning in Life. Personality and Social Psychology
Bulletin, 10.
Vinay, ,. S. (2015). A comparison of test–retest variability and time efficiency of auditory thresholds
measured with pure tone audiometry and new early warning test. Applied Acoustics, 7.