Analysis of Transport Data in NSW: Statistics Study Material

This study material analyses statistical data to determine the commonly used mode of transport in NSW, Australia and provides recommendations on areas where improvements or new developments should be made. It includes single and two variable analysis of datasets and a conclusion with future research recommendations.

University
Statistics
by
Your Name
Date
 <Your Name> 2018 1 of

Section 1
Introduction
The manner in which individuals travel to their places of work and learning institutions
influences their physic activity level. Due to this, surveys are carried out to assist in planning
of physical activity and model travel promotions in institutions and other places in Australia
that require travelling (Rissel, Mulley and Ding, 2013). This paper is there aimed at analysing
statistical data to determine the commonly used mode of transport and provide
recommendations on areas where improvements or new developments should be made.
Datasets
Dataset is a secondary data since it is collected from a secondary source; Australian website
for transport and is a subset of the data “Opal Tap on and Tap off location- 8th to 14th August
2016” provided by the transport for NSW Open data (Opendata.transport.nsw.gov.au, 2016).
It has got five variables; mode, tap, loc and count. Mode is a categorical variable with cases;
bus, train, ferry and light trail indicating the type of public transport used. Tap is a
categorical variable with cases; on and off indicating whether it’s a tap on or a tap off. Loc is
a categorical variable with cases; train stations and postal codes. Count is a numerical
variable indicating the count of the mode of transport. Date is a quantitative continuous
variable indicating when the tape was held (Bruce, 2015).
Dataset 2 is primary data is collected from a one-on-one survey for 160 individuals (Fowler,
2009). This dataset has three variables, date is quantitative continuous variable indicating
the date when it was collected, gender is a categorical variable with two case; male of
female indicating the sex of the person interviewed. Mode is categorical variable with cases
indicating mode of transport used (Bruce, 2015).
 <Your Name> 2018 2 of

Section 2
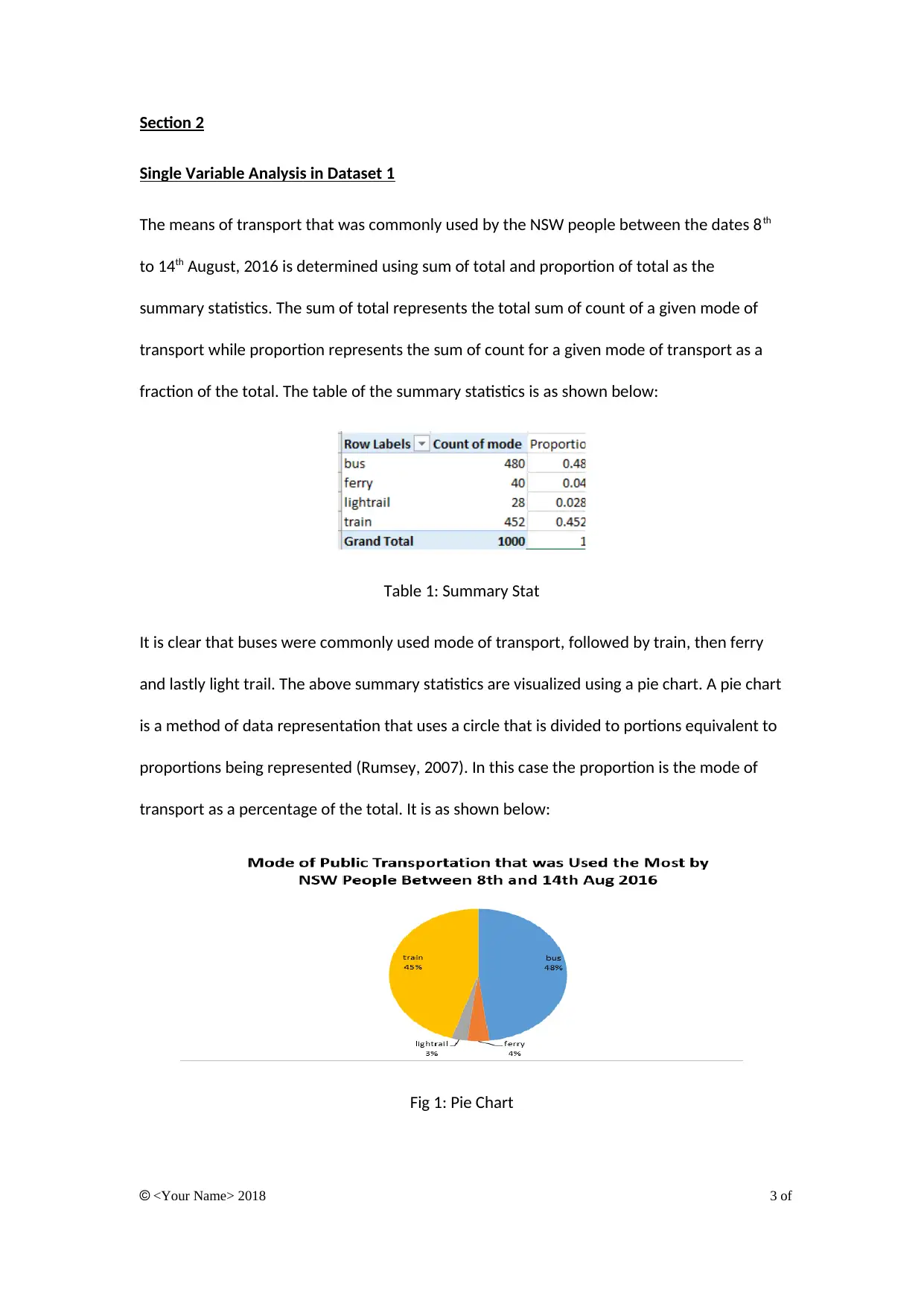
Single Variable Analysis in Dataset 1
The means of transport that was commonly used by the NSW people between the dates 8th
to 14th August, 2016 is determined using sum of total and proportion of total as the
summary statistics. The sum of total represents the total sum of count of a given mode of
transport while proportion represents the sum of count for a given mode of transport as a
fraction of the total. The table of the summary statistics is as shown below:
Table 1: Summary Stat
It is clear that buses were commonly used mode of transport, followed by train, then ferry
and lastly light trail. The above summary statistics are visualized using a pie chart. A pie chart
is a method of data representation that uses a circle that is divided to portions equivalent to
proportions being represented (Rumsey, 2007). In this case the proportion is the mode of
transport as a percentage of the total. It is as shown below:
Fig 1: Pie Chart
 <Your Name> 2018 3 of

To prove whether more than 50% of the population used the mode with the highest
proportion as their preferred mode of transport, a hypothesis is formulated and tested. Our
sample size is 1000 and the highest proportion for the mode of transport (buses) was 0.48.
To process of formulation and testing of the hypothesis follows the steps below:
Step 1: The initial step is to state the null and alternate hypothesis.
The null hypothesis Ho : P=0.5
The alternate hypothesis H i : P ≠ 0.5
Step 2: Check whether all the conditions for the hypothesis are met
N . p ≥ 10=1000 x 0.5≥ 10=500≥ 10
N . (1− p ) ≥ 10=1000 x ( 1−0.5 ) ≥ 10=500 ≥ 10
All the conditions are met
Step 3: Determine the Z-test statistic.
Z= P^¿−P
√ p (1− p)
n
¿
Z= 0.48−0.5
√ 0.5(1−0.5)
1000
= −0.02
0.0158 =−1.26 ¿ 2 dp
Step 4: Developing a decision rule.
Using the default significance level of 0.05 the decision rule will be to accept the null
hypothesis when the P-value for the z-statistic P(Z>-1.26) =0.104 is within the range of -1.96
to 1.96 (Lock et al., 2013). Since the p value is within the required range, we accept the null
 <Your Name> 2018 4 of

hypothesis and conclude that more than 50% of the population used the mode with highest
proportion as their preferred mode of transport with the specified period.
Section 3
Two Variable Analysis in Dataset 1
To prepare the recommendation on which substation the government should build the
underground railway from to central, the data is filtered with train as the mode of transport,
the three stations required for consideration and count. The data is filtered in excel using the
filter function (Linoff, 2008). Once the data is filtered for the required variables the online
stat-key statistic tool is used for analysis(Lock5stat.com, 2018). The summary statistics for
the filtered data is as shown below:
Table 2: Summary Statistics 2
The data above is visualized with the aid of the box plot shown below. A box plot visualizes
data in terms of the median indicating also the direction of skewness for the data.
 <Your Name> 2018 5 of

Fig 2: Box Plot
From the summary statistics and the box plot it is evident that Parramatta station offers the
greatest of service compared to the rest of the stations therefore it would be okay to
recommend to the NSW government to construct the underground station from the
Parramatta station to central to ease the services in the station.
To discern whether there is a difference in the mean for count and taps, hypothesis at 5%
significance level is carried out in stat-key software. The null hypothesis in this case is that
there is no difference between means while the alternate hypothesis is that there is a
difference between means. The first step involves determining the sample sizes and the
means. The result for the means is as shown below:
Table 3: Sample means and sizes
 <Your Name> 2018 6 of

From the above table, the sample sizes are both greater than 30 and the standard deviation
for a given sample is not twice as much as the other hence all the conditions for the
hypothesis test are met.
Step 2 involves determining the degrees of freedom of the numerator and denominator
using the ANOVA table. The results for the degrees of freedom is as shown below:
Table 3: Degrees of Freedom
The degree of freedom for the numerator is 1 while that of the denominator is 998.
In step three a graph of F distribution that will also indicate the p value is drawn and is as
shown below:
 <Your Name> 2018 7 of

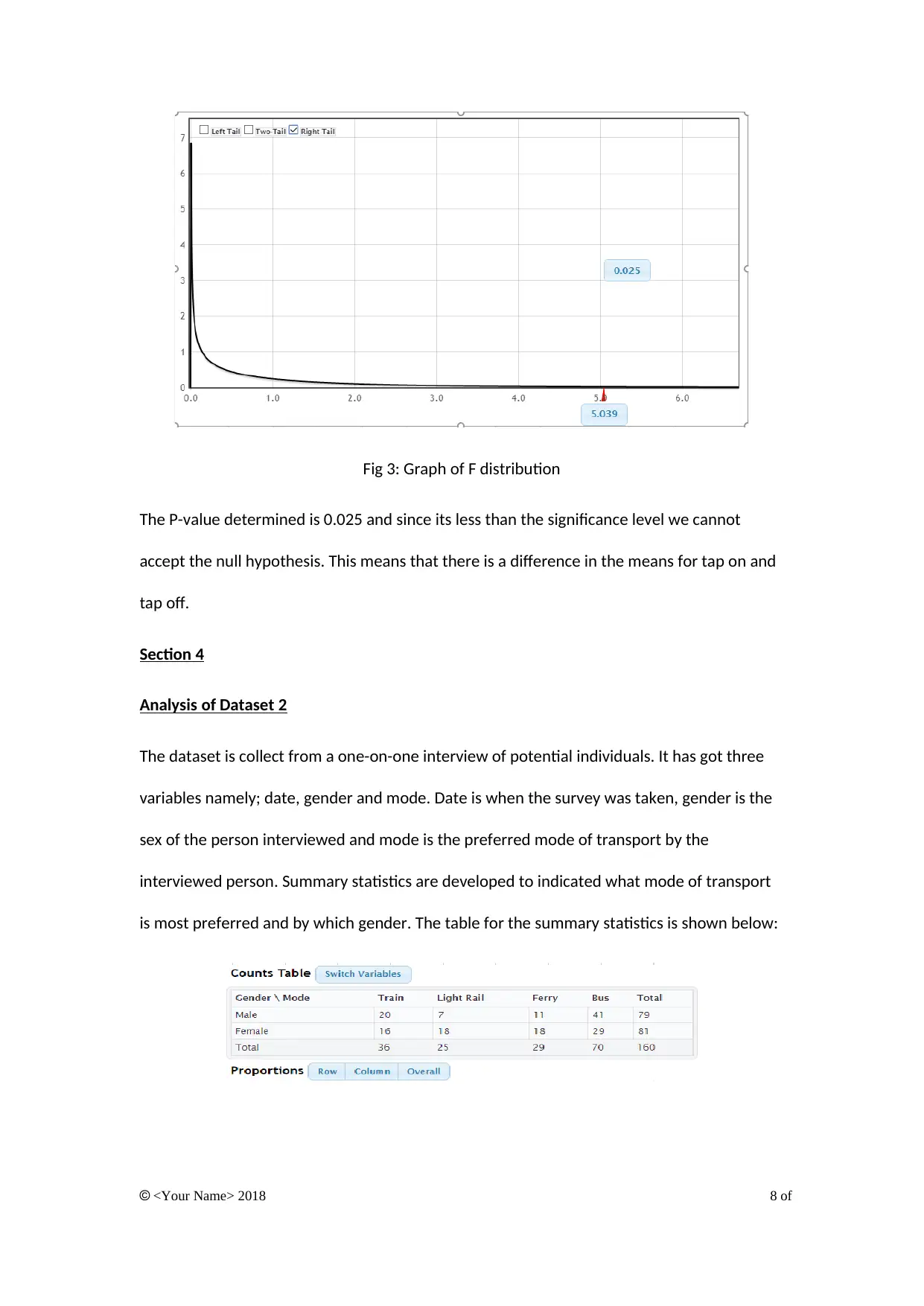
Fig 3: Graph of F distribution
The P-value determined is 0.025 and since its less than the significance level we cannot
accept the null hypothesis. This means that there is a difference in the means for tap on and
tap off.
Section 4
Analysis of Dataset 2
The dataset is collect from a one-on-one interview of potential individuals. It has got three
variables namely; date, gender and mode. Date is when the survey was taken, gender is the
sex of the person interviewed and mode is the preferred mode of transport by the
interviewed person. Summary statistics are developed to indicated what mode of transport
is most preferred and by which gender. The table for the summary statistics is shown below:
 <Your Name> 2018 8 of

Table 4: Summary Statistics 3
The data is visualized with the aid of a stacked bar chart. A stacked bar chart is similar to the
normal bar chart only that it is used for two categorical variables.
Fig 4: Stacked Bar Chart
From the stacked bat chart and the summary statistics, it’s clear that most people prefer
buses to other modes of transport, followed by train, ferry and last in the list is light trail.
Most male prefer bus to women, same case with the train. However, for the ferry and light
rail the contrary is the truth.
Section 5
Discussion and Conclusion
The data analysis performed indicate that most people prefer buses and train for transport.
This can be attributed to the services offered by the various stations of the buses and the
train, ease of access, flexible services and reduced cost. On the other hand, it is clear that
Parramatta train station offers most of the services hence the NSW government should build
the underground railway to central form this station. Future research should be conducted
to examine what factors attract customers to their preferred mode of transport and the
 <Your Name> 2018 9 of

patterns in which the various modes of transport are used so that the government can set
priorities during planning, modelling and development.
 <Your Name> 2018 10 of

References
Bruce, P. (2015). Introductory statistics and analytics. New Jersey: Wiley.
Fowler, F. (2009). Survey research methods. 4th ed. London: Sage Publication.
Linoff, G. (2008). Data analysis using SQL and Excel. Indianapolis, Ind.: Wiley Pub.
Lock, R., Lock, P., Morgan, K., Lock, E. and Lock, D. (2013). Statistics: Unlocking the power of
data. Wiley.
Lock5stat.com. (2018). Theoretical distribution. [online] Available at:
http://www.lock5stat.com/StatKey/theoretical_distribution/theoretical_distribution.html#n
ormal [Accessed 21 Sep. 2018].
Opendata.transport.nsw.gov.au. (2016). Opal Tap On and Tap Off | TfNSW Open Data Hub
and Developer Portal. [online] Available at:
https://opendata.transport.nsw.gov.au/dataset/opal-tap-on-and-tap-off [Accessed 21 Sep.
2018].
Rissel, C., Mulley, C. and Ding, D. (2013). Travel mode and physical activity at Sydney
University. International Journal of Environmental Research and Public Health, [online] 10(8).
Available at: http://www.mdpi.com/1660-4601/10/8/3563/pdf [Accessed 21 Sep. 2018].
Rumsey, D. (2007). Intermediate statistics for dummies. 1st ed. Hoboken, N.J.: Wiley.
 <Your Name> 2018 11 of