Transport Phenomena Problems

1
TRANSPORT PHENOMENA
Solution

2
Solving momentum and continuity equations for u∧v which enables to determine
the thickness of the boundary layer and drag friction coefficient. In obtaining the
results, Boundary partial differential equation is reduced to a single differential
(Ordinary) equation (Hermann Schlichting, 2016).
The stream function satisfying continuity equation is given by:
u ( x , y ) = ∂ Ψ
∂ y
v ( x , y ) =−∂Ψ
∂ x
Substituting the values of u and v that are expressed in relations to stream
function to x-momentum we come up with the following equation;
∂Ψ
∂ y
∂2 Ψ
∂ x ∂ y - ∂Ψ
∂ x
∂2 Ψ
∂ y2 = μ
ρ
∂3 Ψ
∂ y3
According to Balsius there is no length scale in a flat plate, the velocity profile
(non-dimensional) remains constant when plotted against coordinates normal to
the surface (wall) i.e.
u
U∞
=¿ function η
In which η is a parameter that is dimensionless that is related to y
g (x) where g( x )
and δ (x) (boundary layer thickness) are related. Now taking the points of the
plate be A and B, then g(x ) is expressed as a function of x coordinates along the
plate and B (constant) i.e.
η ( x , y ) =B xq y
The stream function can also be expressed as a function of x, A (constant) and f ( η
)

3
Ψ ( x , y ) = A x p f ( η)
To determine the unknown parameters, boundary conditions are used in
substitution of stream function derivatives as shown below (Lachmann, 2014).
Substituting the above equations we come up with one equation which is:
( p+q ) f ' 2− pf f ¿= μ
ρ
B
A x− p +q+1 f ¿
The relationship between p and q can be obtained from the similarity equation which is
independent of therefore;
− p+q +1=0
Set of equations are solved by use of boundary condtions.The equation includes;
u ( x , 0 ) =0
∂Ψ
∂ y ( x ,0 )=0
AB x p+ q f ' (0)=0
Implying a non-trivial s0lution f '( 0)=0 and the 2nd boundary condition becomes;
v ( x ,0 )=0
−∂ Ψ
∂ x ( x ,0 )=0

4
− Ap x p−1 f ( 0 ) −AB qyx p+ q−1 f ' (0)=0
Given f '( 0)=0,non-trivial solution is f (0)=0 , then the final boundary condition
becomes,
u ( x , ∞ ) =U∞
∂Ψ
∂ y ( x ,∞ ) =U∞
AB x p+ q f ' (∞)=U∞
For satisfaction purposes we set the following;
AB F'
∞=U∞
P+q=0 .
Using the two equations (-p+q+1=0 and p+q=0) we can get the value of p and q
p= 1
2
q=−1
2
For the equationf '( ∞)=1 and AB= U∞, we can derive the dimensionless equation below,
μ
ρ
B
A =1
Then,
B= √ U∞ ρ
μ
A= √ U∞ μ
ρ
Then the unknown parameters are obtained and substituted in the momentum equation
and the 3rd ordinary differential expression is obtained. The equations also have its
boundary equations as shown below. 2 f ' ' ' + f f ' =0

5
f (0)=0
f '( 0)=0
f '( ∞)=0
Given the expressions for η and the stream function as: ψ= √ vx V ∞ f (η) (Expressed in
terms of f) and η= y √ V ∞
vx
The 3rd order ordinary differential equation (nonlinear) is solved by use of Runge-Kutta
formula (method).This formula integrates in small stages along y axis starting from the
surface (wall).Value of boundaries conditions are assumed and the large value of η is
checked if the condition f ' (∞)=1 (I.Terekhov, 2014).
By use of shooting method we can be able to find the value of f ' ' ( 0 )=¿0.3320
To find x-components of velocity profile, derivatives of Ψ with respect to y as shown
below,u ( x , y )= ∂ Ψ
∂ y
u ( x , y ) =U ∞ f ' (η)
The results graphs are as shown below.

6
To find the y components of velocity,Ψ is derived with respect to x.
v ( x , y ) =−∂Ψ
∂ x
The dimensionless expression is obtained i.e.
v ( x , y)
U∞
R ex
1
2 =−1
2 (f ( η )−η f ' ( η ))
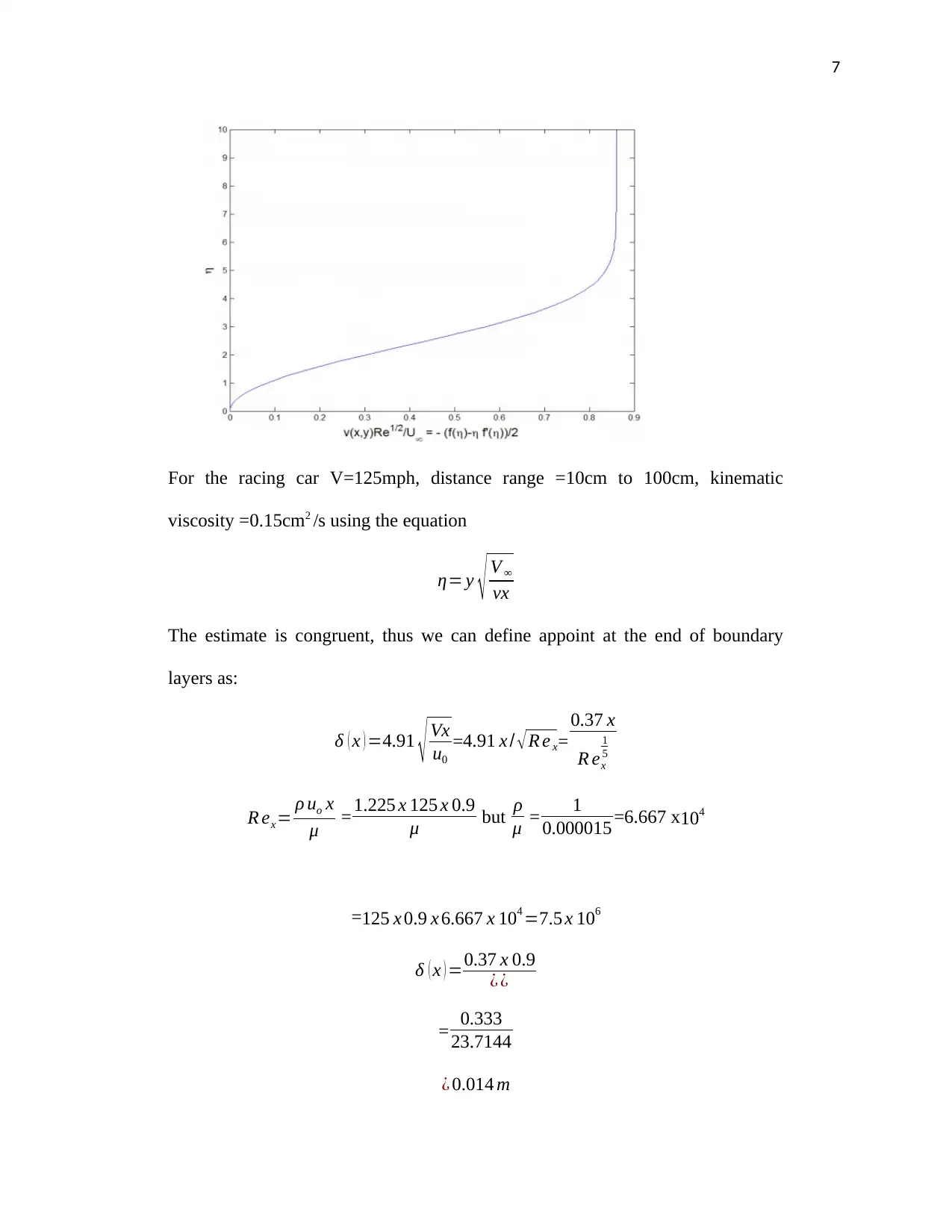
Y-component velocity profile is as shown below.

7
For the racing car V=125mph, distance range =10cm to 100cm, kinematic
viscosity =0.15cm2 /s using the equation
η= y √ V ∞
vx
The estimate is congruent, thus we can define appoint at the end of boundary
layers as:
δ ( x ) =4.91 √ Vx
u0
=4.91 x / √ R e x=
0.37 x
R ex
1
5
R ex= ρ uo x
μ = 1.225 x 125 x 0.9
μ but ρ
μ = 1
0.000015 =6.667 x104
=125 x 0.9 x 6.667 x 104 =7.5 x 106
δ ( x ) =0.37 x 0.9
¿ ¿
= 0.333
23.7144
¿ 0.014 m

8
Drag force is givenby FD =CD ρ A V 2
2
0.001 x 1.225 x 0.9 x 0.014 x 1252
2
¿ 0.121lbf
Porous surfaces reduces the amount of drag force exerted at the surface.
References
Hermann Schlichting, K. G. (2016). Boundary-Layer Theory. London: Springer.
I.Terekhov, V. (2014). Flow and Heat and Mass Transfer in Laminar and
Turbulent Mist Gas. London: Springer.
Lachmann. (2014). Boundary Layer and Flow Control. New York: Elsevier
science.

9