Analytical Methods for Engineers - Trigonometric Methods TMA 2

This document presents the solved assignment for Trigonometric Methods under the Analytical Methods for Engineers module. It includes detailed solutions to five questions covering topics such as calculating angles and distances using trigonometric principles, analyzing wave equations, applying trigonometric identities, and performing complex number calculations. The solutions demonstrate a clear understanding of trigonometric functions, identities, and their applications in engineering contexts. The assignment also includes Argand plots and calculations of power using complex numbers.

Running head: TRIGONOMETRIC METHODS
Trigonometric Methods
Name of the student
Name of the university
Author’s note

1TRIGONOMETRIC METHODS
Table of Contents
Answer 1..........................................................................................................................................2
Part a............................................................................................................................................2
Part b............................................................................................................................................3
Part c............................................................................................................................................3
Answer 2..........................................................................................................................................3
Part a............................................................................................................................................3
Part b............................................................................................................................................3
Part c............................................................................................................................................3
Part d............................................................................................................................................3
Part e............................................................................................................................................4
Part f.............................................................................................................................................4
Answer 3..........................................................................................................................................4
Part a............................................................................................................................................4
Part i.........................................................................................................................................4
Part ii........................................................................................................................................4
Part iii.......................................................................................................................................5
Part b............................................................................................................................................5
Answer 4..........................................................................................................................................5
Part a............................................................................................................................................5
Part b............................................................................................................................................6
Answer 5..........................................................................................................................................7
Part a............................................................................................................................................7
Part b............................................................................................................................................7
Part c............................................................................................................................................8

2TRIGONOMETRIC METHODS

3TRIGONOMETRIC METHODS
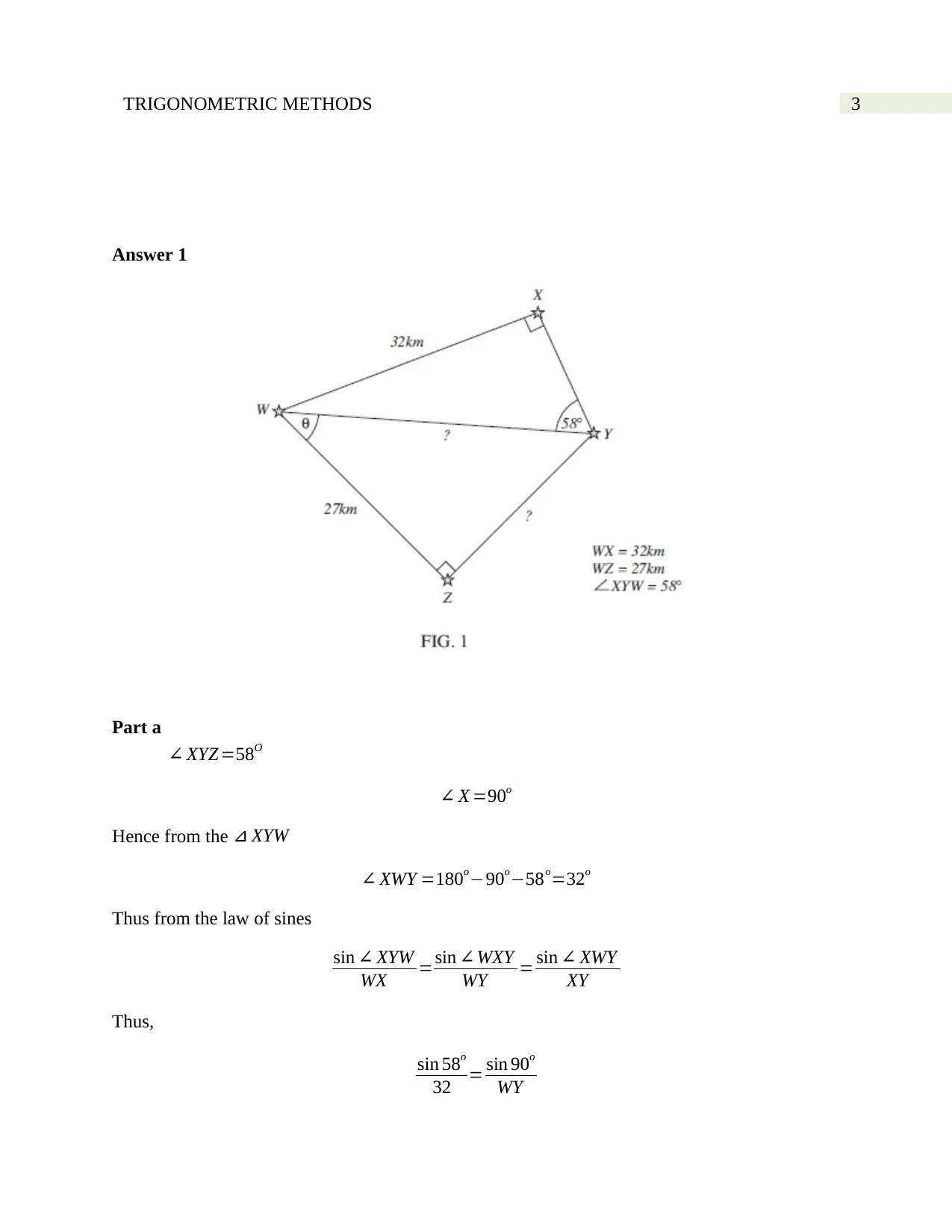
Answer 1
Part a
∠ XYZ =58O
∠ X =90o
Hence from the ⊿ XYW
∠ XWY =180o−90o−58o=32o
Thus from the law of sines
sin ∠ XYW
WX =sin ∠WXY
WY = sin ∠ XWY
XY
Thus,
sin 58o
32 = sin 90o
WY

4TRIGONOMETRIC METHODS
WY =32∗sin 90o
sin 58o = 32∗1
0.848 =37.73 ≈ 38
Hence, WY = 38km
Part b
∠ XWZ=90o
∠ XWY =32o
Hence, ∠ YWZ=∠ XWZ−∠ XWY =90o−32o=58o
θ=∠ YWZ=58o
Part c
From Pythagoras theorem W Y 2=W Z2+ Z Y 2
382=272+ Z Y 2
Thus, Z Y 2=382−272=1444−729=715
Hence, ZY ≈27km
Answer 2
i=15 sin(100 πt+ 0.6)
Part a
The amplitude A = 15
Part b
The frequency (ω) of the equation of wave is 100π.
Part c
The period (T) of the equation of wave is (T = 2 π
ω ). Here, ω = 100π. Hence, the period of
the wave equation is T = 2 π
100 π =0.02

5TRIGONOMETRIC METHODS
Part d
When t= 0 the initial phase angle = 0.6 radians
2 π radians=360o
0.6 radians=0.6∗360o
2 π =0.6∗57.29o ≈34o
Part e
When t = 2.5s
i=15 sin ( 2.5∗100 π +0.6 )=15 sin ( 125∗2 π +0.6 ) =15 sin 0.6
i=15∗0.01047=0.15705
Since sin ( 2 πk + x ) =sin x
Part f
When phase angle = π
2 first peak occurs.
Thus, 100 πt +0.6= π
2
Since 0.6 is in degrees converting it into radians 0.6∗π
180 = π
300
Thus, 100 πt + π
300 =π /2
 100 t+ 1
300 = 1
2
 100 t=1
2 − 1
300 = 149
300 =0.4967
 Thus, t = 0.004967

6TRIGONOMETRIC METHODS
Answer 3
Part a
Part i
cos ( 270o−θ )=cos 270o cos θ+sin 270o∗¿ sin θ ¿
¿ 0∗cos θ+ (−1 )∗sin θ=¿−sin θ ¿
Part ii
sin (270o−θ ) =sin 270o∗cos θ−cos 270o∗sin θ
¿−1∗cos θ−0∗sin θ=−cos θ
Part iii
cos ( 270o +θ ) =cos 270o cos θ−sin 270o sin θ
¿ 0∗cos θ− (−1 )∗sinθ=sin θ
Part b
V 1=3 sin ωt
V 2=2 cos ωt
V 3=V 1 +V 2 =R sin (ωt +α )
R sin ( ωt +α ) =3 sin ωt +2 cos ωt
Hence, R= √32+22 = √13
α =atan 2
3 =33.7o
Thus V 3=R sin ( ωt + α ) = √ 13 sin( ωt+ 33.7o )=3 sin ωt +2 cos ωt
The frequency of the resultant = ωtwhich is equal to the frequency of the initial ωt

7TRIGONOMETRIC METHODS
Answer 4
Part a
Z1 =4+ j 10
Z2 =12− j 3
Z= Z1 Z2
Z1+Z2
= ( 4+ j10 )∗(12− j 3)
4 + j 10+12− j3
¿ 48− j 12+ j120− j2 30
16 + j 7 = 48+ j108+30
16+ j7 = 78+ j108
16+ j7
¿ ( 78+ j 108 )∗(16− j7)
(16+ j 7 )∗(16− j 7) = 1248− j546 + j 1728− j2 756
256− j2 49 = 1248+ j 1182+756
256 +49
Z=2004 + j 1182
305 =6.57+ j3.875 (rectangular form)
Polar form
r = √6.572+ 3.8752= √ 58.18=7.63
θ=arctan 6.57
3.875 =arctan 1.69=0.53
Thus Z=7.63 ecos 0.53 +sin0.53
Part b
Z1 =2+ j 2
Z2 =1+ j 5
Z3 = j 6
Y = 1
Z1
+ 1
Z2
+ 1
Z3
¿ 1
2+ j 2 + 1
1+ j 5 + 1
j 6

8TRIGONOMETRIC METHODS
¿ 2− j 2
(2+ j2)(2− j2) + 1− j 5
(1+ j5)(1− j 5) + − j 6
( j6)(− j6)
¿ 2− j2
4− j2 4 + 1− j 5
1− j2 25 + − j6
− j2 36
¿ 2− j 2
4+ 4 + 1− j5
1+25 − j 6
36
¿ 2− j 2
8 + 1− j5
26 − j
6
¿ 0.25− j 0.25+0.038− j 0.19− j0.16
¿ 0.288− j 0.6
Polar form
r = √ 0.2882+0.62= √ 0.083+0.36= √ 0.443=0.67
θ=arctan −0.6
0.288 =−1.13 rad=−64.7o
Z=0.67 ecos (−64.7 o )+ sin(−64.7¿¿o )¿
Answer 5
Part a
V =40+ j35
I =6+ j3

9TRIGONOMETRIC METHODS
Figure 1: Argand Plot
Part b
The angle between voltage and real axis
tan α= 35
40 =0.875
Hence, α=0.7188 rad
The angle between current and real axis
tan β= 3
6 =0.5
Hence, β=0.4636 rad
ϕ =0.7188−0.4636=0.2552 rad=14.6o
cos 14.6o=0.9676
Part c
V =40+35 j
The magnitude of V = √(40¿¿ 2+352 )= √(1600+1225)= √2825=53.15¿

10TRIGONOMETRIC METHODS
I =6+3 j
The magnitude of I = √ 62 +32= √ 36+ 9= √ 45=6.71
Hence, P=|V |∗|I |∗cos ϕ=53.15∗6.71∗0.9676=345.08 watt