Ladder Heights, Trigonometric Graphs, Resultant Forces, and Volume Calculations: Summary of Given Data

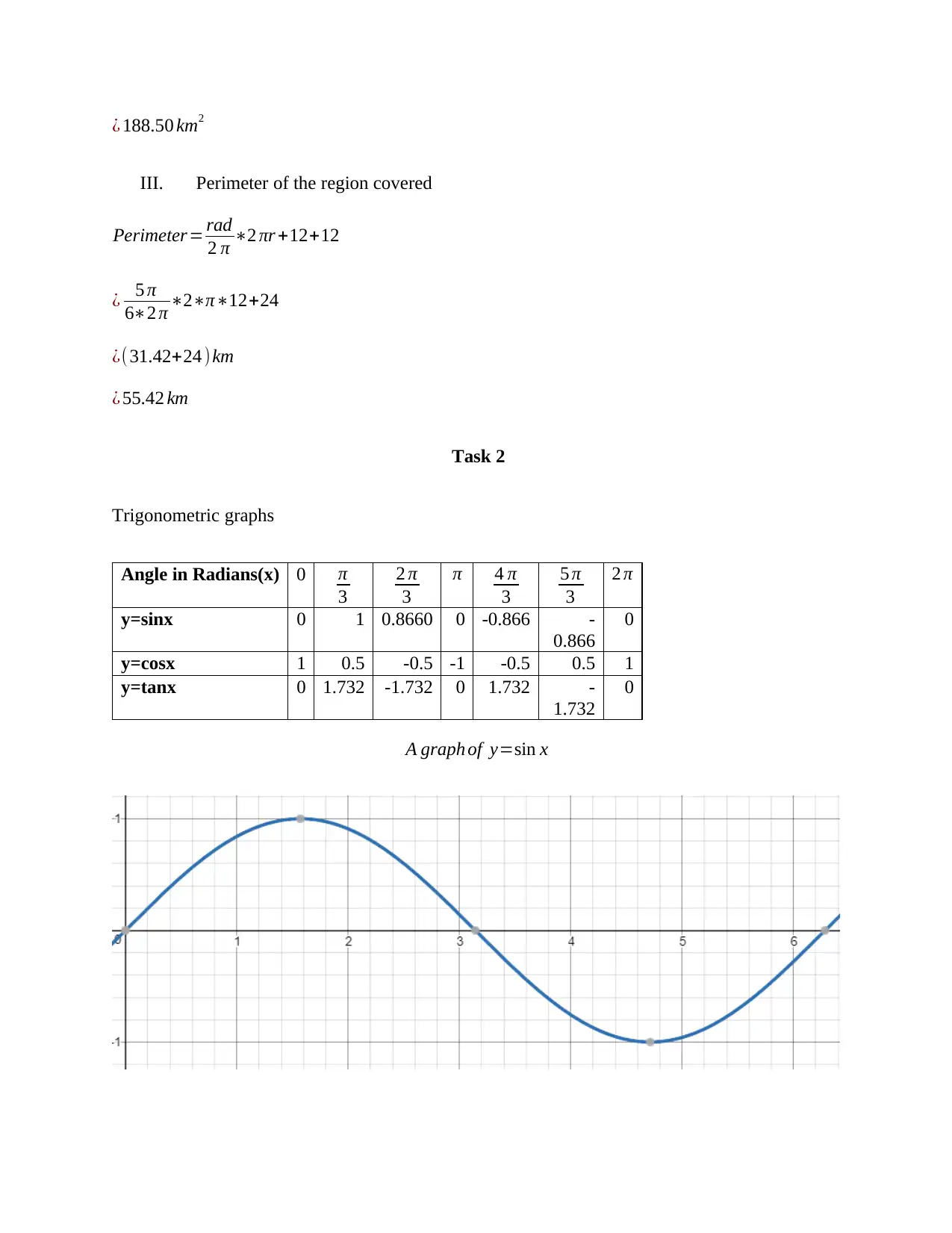
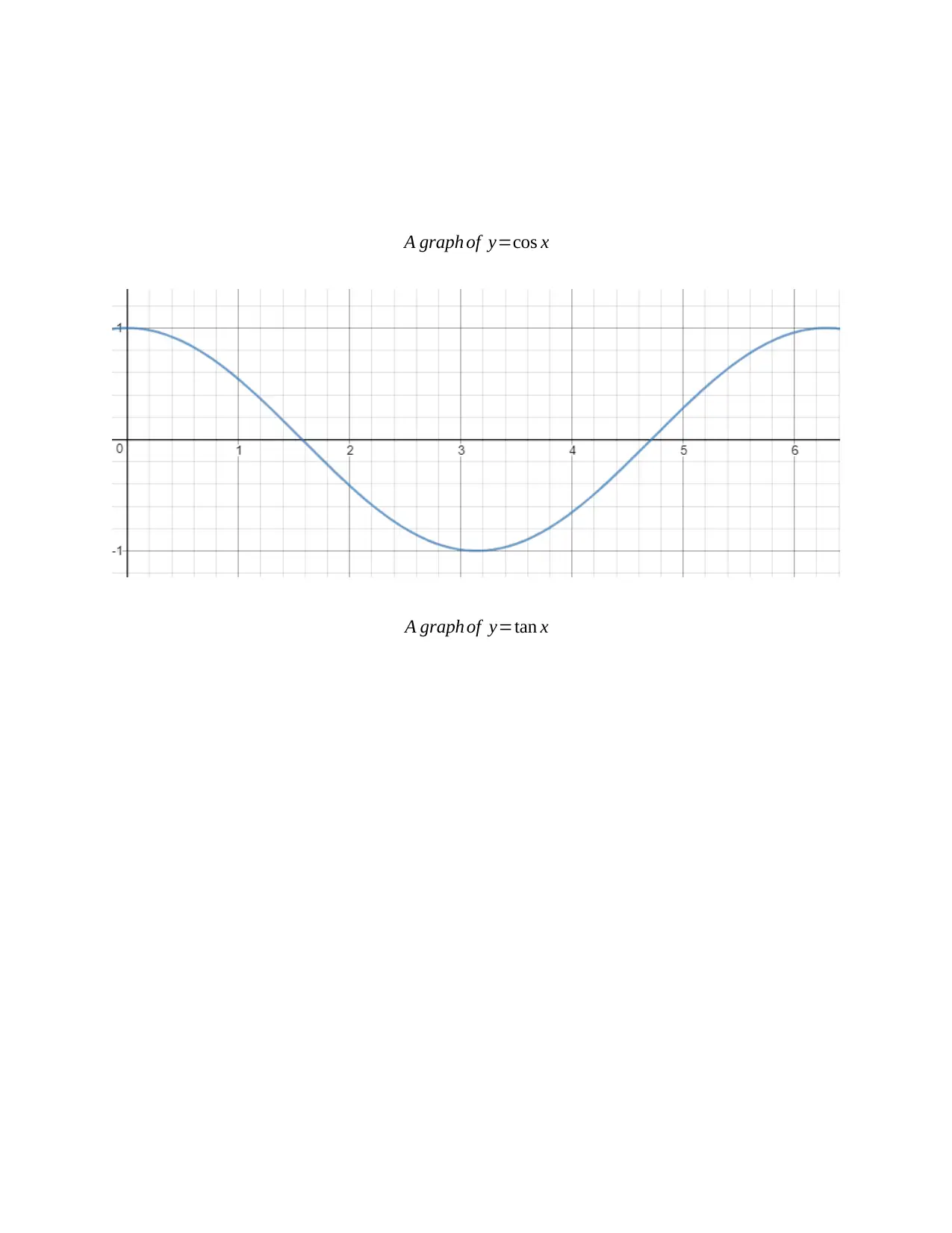
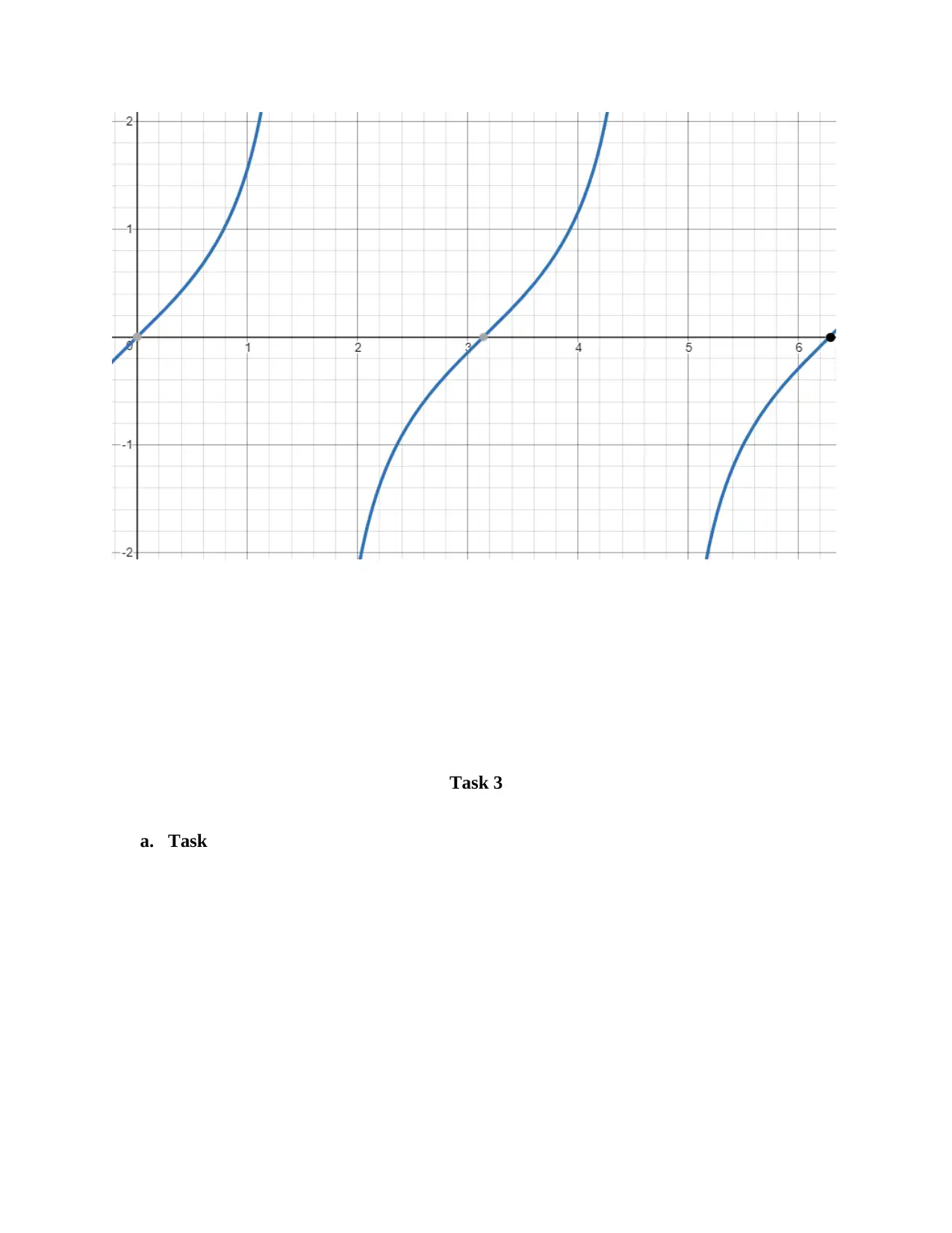
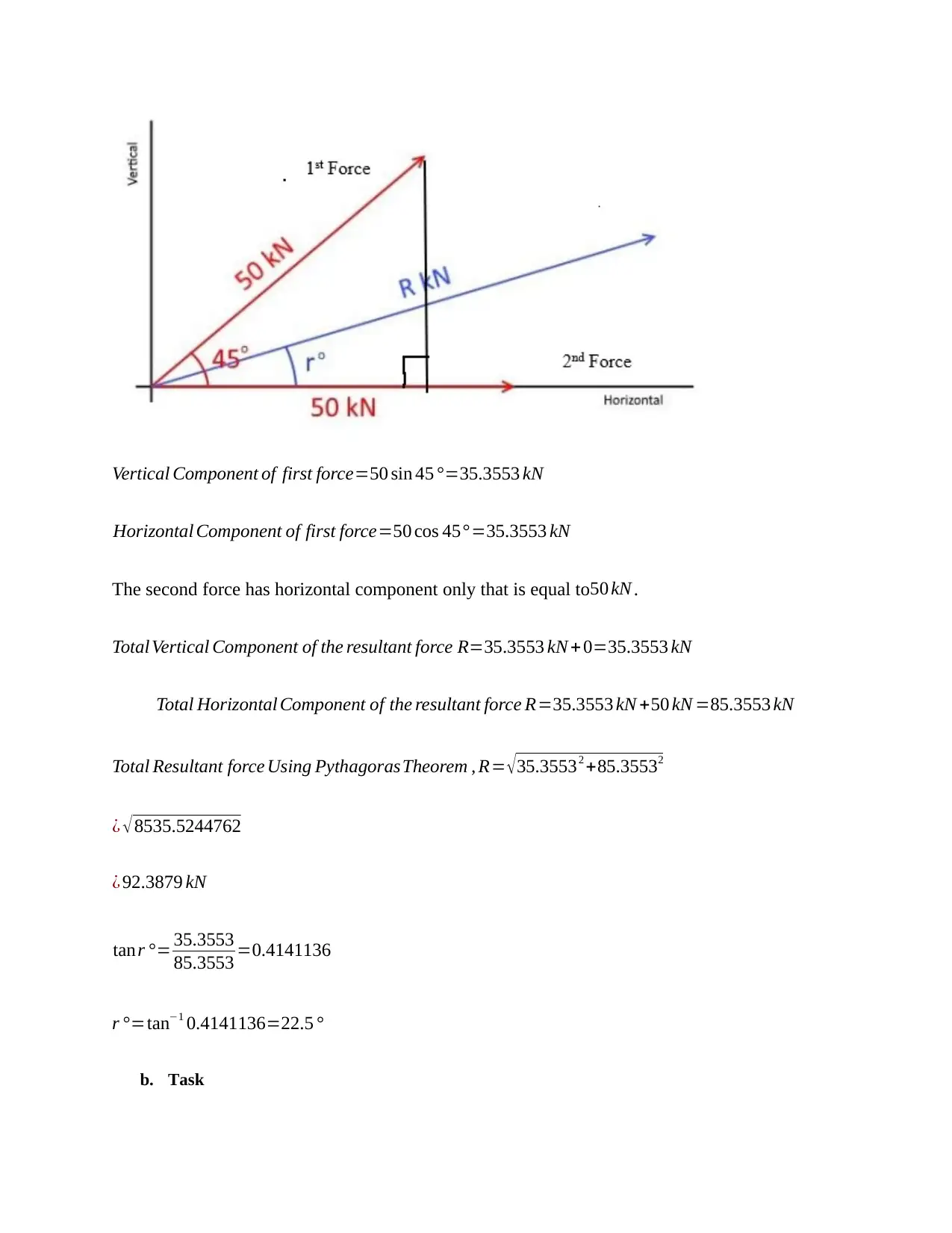
Task 1 involves calculating the height, length, and angle of a ladder. Task 2 displays trigonometric graphs. Task 3 involves calculating the resultant force of two components and the length and angle of a tie. Task 4 calculates the volume and surface area of an open cylinder and the volume of a triangular prism.