Two-Port Networks: Electrical & Electronic Principles TMA 2 (v3.1)

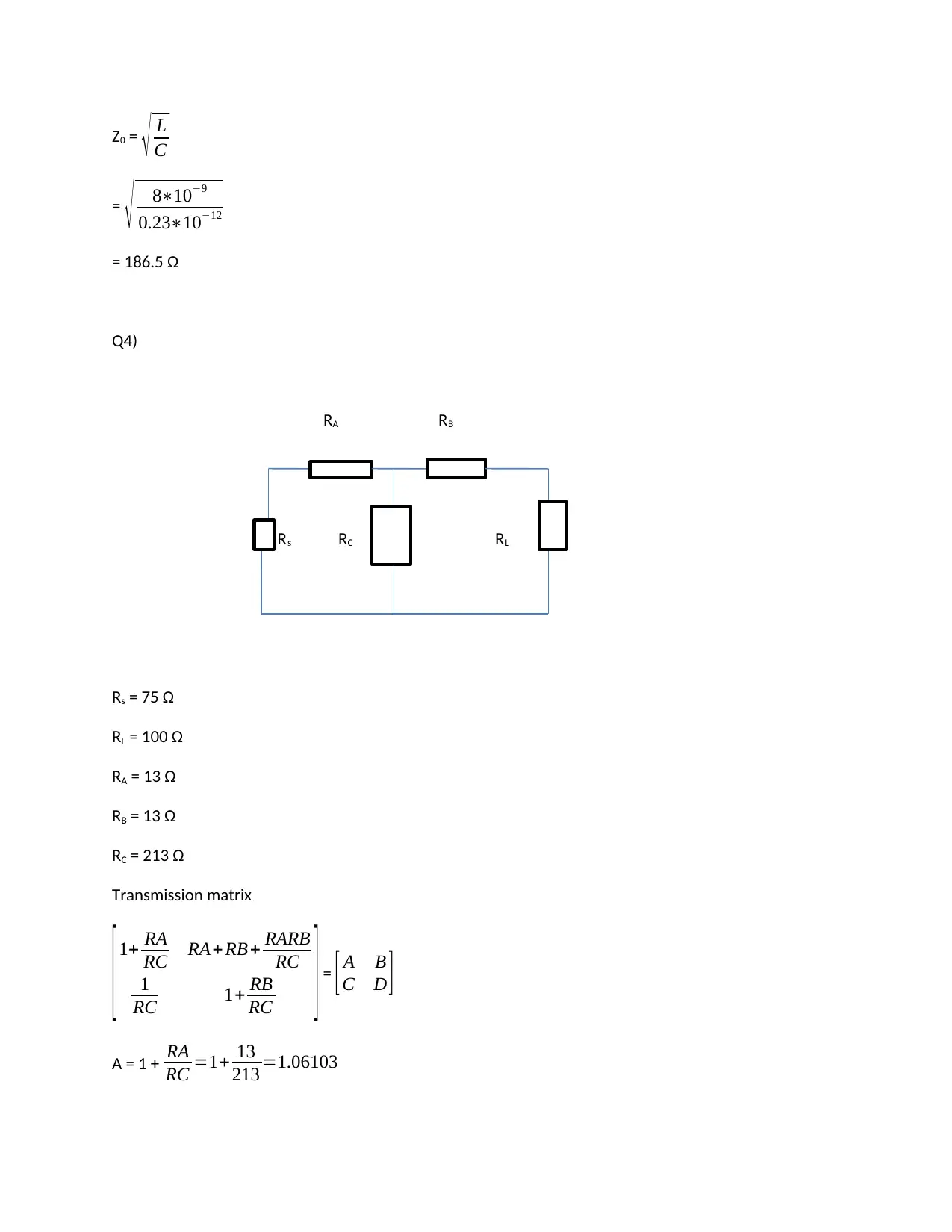
This assignment solution covers various aspects of two-port networks within the context of electrical and electronic principles. It includes calculations of impedance parameters (Z parameters), analysis of transmission lines including determination of phase change and input impedance, and discussion of distortionless and lossless transmission lines. The solution also involves calculating characteristic impedance and surge impedance. Furthermore, it addresses the analysis of T-networks, including the determination of the transmission matrix and insertion loss. The assignment also covers complex ABCD parameters for transmission lines, calculating sending end voltage and current, and power absorbed from the supply. Finally, it includes calculations related to distributed parameters of a transmission line and their impact on ABCD parameters. Desklib provides this solution and many other resources for students.

MODULE TITLE : ELECTRICAL AND ELECTRONIC PRINCIPLES
TOPIC TITLE : TWO-PORT NETWORKS
TUTOR MARKED ASSIGNMENT 2 (v3.1)
Q1)
8Ω Zc
8Ω Za 0Ω
6Ω Zb 6Ω
Za = 8.0 Ω
Zb = 6.0 Ω
Zc = 0.0 Ω
Now Z11 = open circuit input impedance
Z11 = Za + Zb = 8 + 6 = 14Ω
Z11 = 14Ω
Z12 = open circuit reverse transfer impedance
Z12 = Zb = 6Ω
Z12 = 6Ω
Z21 = open circuit forward transfer impedance
Z21 = Zb = 6Ω
Z21 = 6Ω
Z11 = open circuit driving point impedance
Z22 = Zb + Zc = 6 + 0 = 6Ω

Z22 = 6Ω
Z= [ 14 6
6 6 ]
Q2) given transmission line length
L = 0.4d
Determination of phase change Bl
Bl = B(0.4d)
Where d = wavelength
Bd = 2 π
Bi = (0.9)(2 π ¿ = 0.8 π
b) given z0 = 50Ω
l = 0.4d
zL = 40 + j30Ω
Bl = 0.8 π=1140
Zin = Z0* Z 2 cosBl+ jZ 0 si nBl
Z 0 cosBl + jZ 2 sinBl
= 50* ( 40+ j30 ) cos ( 14490 ) + j 50 sin 1440
50 cos ( 1440 ) + j∗40+ j 30 ¿ sin (1440 )¿
Zin = 50*−32.36− j24.27+ j 29.38
−40.45−17.63+ j23.51
Zin = 25.466 + j5.909 Ω
Q3a)
Transmission line is said to be distortion less when attenuation constant α is frequency independent
and the phase shift constant β is linearly dependent on frequency.

Transmission line is said to be lossless if the conductivity σ c = α and the electric medium between the
line is lossless that is conductivity σ d = 0
b) Given data
R = 2.0 Ω/m
L = 8.0 nH/m
G = 0.5 ms/m
C = 0.23 pF/m
Z = v + jwl = 2 + j(2* π∗109∗8∗10−9
2 = 2 + j50.26598
= 50.305 ⌊ 87.72¿ ¿
Y = g + jwc = 0.5 * 10-3 + j(2π∗fc)
= 0.5 *10-3 + j(2 π∗109∗0.23∗10−12
Y = 5.0 *10-4 + j1.445 *10-3
= 1.529 *10-3 ⌊ 70.9¿ ¿
Zc = characteristic impedance = √ Z
Y
Zc = √50.305 ⌊ 87.72 ¿ ¿ ¿
1.529∗10−3 ⌊ 70.9 ¿ ¿
Zc = 181.385⌊ 8.41¿ ¿
γ= √YZ = √1.529∗10−3∗50.305 ⌊ 87.72+70.9
2 ¿ ¿
= 0.2773⌊ 79.31¿ ¿
γ=0.05143+ j 0.27248
γ=α + jβ
α =0.05143
β=0.27248
Z0 = surge impedance on natural load

Z0 = √ L
C
=
√ 8∗10−9
0.23∗10−12
= 186.5 Ω
Q4)
RA RB
Rs RC RL
Rs = 75 Ω
RL = 100 Ω
RA = 13 Ω
RB = 13 Ω
RC = 213 Ω
Transmission matrix
[ 1+ RA
RC RA+ RB+ RARB
RC
1
RC 1+ RB
RC ] = [ A B
C D ]
A = 1 + RA
RC =1+ 13
213 =1.06103

B= RA + RB + RARB
RC =13+13+ 13∗13
213
C = 1
RC = 1
213 =4.694∗10−3
D= 1 + RB
RC =1+ 13
213 =1.06103
Insertion loss of T- network in db is
AIL = 20log[ ARL+B+ ( CRL+ D ) Rs
Rs+RL ¿
= 20log[ 1.06103∗100+26.7934 + ( 4.694∗10−3∗100+1.06103 ) 75
75+100 ¿
= 3.017 db
Q5a)
Given complex ABCD equation
Vs = VR(A1 + jA2) + IR(B1 + jB2)
Is = VR(C1 + jC2) + IR(D1 + jD2)
Where the subscripts s and R for sending end and receiving end respectively
Open circuited received voltage VR = 88.9 kV

Transmission line is open circuited
IR = 0
Hence
Vs = VR(A1 + jA2)
Is = VR(C1 + jC2)
Given table
A1 0.8698 B1 47.94 Ω
A2 0.03542 B2 180.8 Ω
C1 0 S D1 0.8698
C2 0.001349 S D2 0.03542
Therefore
Vs = 88.9(0.8698 + j0.03542)
Vs = 88.9(0.87⌊ 2.33 ¿¿ kV
Vs = 77.279 + 3.14j kV
Therefore,
Is = VR(C1 + jC2)
Is = 88.9(0 + j0.001349)
Is = 0.1199 ⌊ 900 ¿ ¿
Is = 11.9⌊ 900 ¿ ¿ A
Power absorbed from supply (PSO) = Vs * Is*
PSO = (77.279 + 3.14j)(-119.9j)
= 376.486 – 9265.75j kW
b)
1
2 Rδx 1
2 Rδx
1
2 Rδx 1
2 Lδx

Cδ x Gδx
[ A B
C D ] =
[ 1+ 1
2 ( R+ jwL ) ( G+ jwC ) δ x2 ( R+ jwL ) δx+ 1
4 ( R+ jwL ) 2 ( G+ jwC ) δ x3
(G+ jwC)δx 1+ 1
2 ( R+ jwL ) ( G+ jwC ) δ x2 ]
A = A1 + jA2
B = B1 + jB2
C = C1 + jC2
D = D1 + jD2
C1 + jC2 = (G + jwC) δx
Here δx=50 km
W = 2 πf =2∗3.14∗50=314
(G + j314C) 50
= 50G + j15700C
C1 = 50G => G = C 1
50
C2 = 15700C => C = C 2
15700
C1 = 0 => G = 0
50 =0
C2 = 0.001349
C = 0.001349
17500

= 85.92 *10-9
= 85.92 nF
A = D = 0.8698 + j0.03542
1 + 1
2 ( R+ jwL ) δx (G+ jwC )δx
= 1 + 1
2 ( R+ jwL)δx¿C1 +jC2)
= 1 + 1
2 ( R+ j 314 L )∗50 ¿0 +j0.001349)
= 1 + (25 R+ j7850 L)δx ¿j0.001349)
= 1 + j0.033725R – 10.589L
Equating the coefficients
0.03542 = 0.033725R
R = 1.05 Ω
1 – 10.589L = 0.8648
10.589L = 0.1352
L = 0.0128 H