Analyse and Model Engineering System

This document provides solutions for various topics in Analyse and Model Engineering System. It includes finding the determinant of a 3x3 matrix, solving closed loops of a D.C. circuit, Gaussian elimination method, matrix solution using inverse matrix, and more.

Analyse and Model Engineering
System

TASK 2.0
2.1 To find the determinant of 3x3 matrix
1 2 3
0 -4 1
0 3 -1
Solution: Using determinant formula of 3 x 3 matrix as
A = a11 a12 a13
a21 a22 a23
a31 a31 a33
then, determinant of A will be calculated by using following formula
A = a11 ( a22 x a33 – a23 x a31) – a12 ( a21 x a33 – a23 x a31) +a13 (a21 x a31 - a22 x a31)
Using this formula, to find determinant of given matrix is given by
can be calculated as
1 2 3
A = 0 -4 1
0 3 -1
then, determinant of A = [ 1 ( -4 x -1 – 1 x3) - 2 ( 0 x -1 – 1 x 0 ) + 3 (0 x 3 – 1 x 0) ]
= [ 1 (4 – 3) – 2 ( 0 – 0) + 3 ( 0 – 0 )]
= 1
1

2.2 Three closed loops of a D.C. Circuit is given by -
2 x + 3 y – 4 z = 26
x – 5 y – 3 z = -87
-7 x + 2 y + 6 z = 12
To determine current flow, by Kirchoff's laws
Solutions: Kirchoff's Laws – As per this law, sum of current flows from different loops is equal
to the sum of current that meets at certain point on a node. To determine, unknown variables in a
closed loop, Kirchoff's second law has been used as Loop Current Analysis of following algebric
algorithms -
2 x + 3 y – 4 z = 26 ...(i)
x – 5 y – 3 z = -87 ...(ii)
-7 x + 2 y + 6 z = 12 ...(iii)
On substituting and simplifying these equations, we get
x = 26 – 3 y + 4 z from equation first,
2
where, by putting this value in equation second equation and simplifying, we get
y = 200 – 2z
13
Now, substituting this value of y in x, we get x = 49 z – 262
26
So, using both value of x and y in equation third to eliminate two variables and convert into
third, we will get -
then,
-7 (49 z – 262) + 2 (200 - 2z) + 6 z = 12
26 13
- 343 z + 1834 + 800 – 8z + 156 z = 312
-195 z = -2322
z = 11.90
so, x = 49 (11.90) – 262 = 12.35 and
26
y = 200 – 2z = 200 – 2 x 11.90 = 13.55
2

13 13
So, x = 12.35, y = 13.55 and z = 11.90
2.22 Find value of x, y, z by using Guassian elimination method
Linear vector equation, in matrix form -
2 3 -4 x = 26
A = 1 -5 3 y = -87
-7 2 6 z = 12
Now, using Guassian Elimination method,
2 3 -4 26
1 -5 -3 -87
-7 2 6 12
Use R1 → ½ R1
1 3/2 -2 13
1 -5 -3 -87
-7 2 6 12
Use R2 → R2 - R1
1 3/2 -2 13
0 -13/2 -1 -100
-7 2 6 12
Use R3 → R3 + 7 R1
1 3/2 -2 13
0 -13/2 -1 -100
0 25/2 -8 103
So, solving this,
we get, x = 10
y = 14
z = 9
3

2.23 Matrix solution using inverse matrix
Let A X = B
2 3 -4 x 26
A = 1 -5 3 X = y B = -87
-7 2 6 z 12
Using inverse matrix -
so, X = B A-1
Now, A-1 = 1 AT
det.A
So, A-1 = 1 -36 27 -33
-21 -26 -16 -25
-11 -10 -13
A-1 = 1 -36 27 -33
-21 -26 -16 -25
-11 -10 -13
So,
x 1 -36 27 -33 26
y = -21 -26 -16 -25 -87
z -11 -10 -13 12
x = 10
y = 14
z = 9
4

3.1
a) Equation of voltage is given by -
vc = 120(1 – e -t/CR ),
Here, R = 47kΩ and C = 15 uF
at t = 0 sec,
vc = 120(1 – e0 )
vc = 0 V
Now, t = 1 sec,
vc = 120(1 – e -1/15x47 )
vc = 120 (1 – e-1/705 )
= 120 (1 – 0.9985)
= 120 x 0.0015 = 0.18V
At time t = 2 sec,
vc = 120(1 – e -2/15x47 )
vc = 120 (1 – e-2/705 )
= 120 (1 – 0.9976)
= 120 x 0.0024 = 0.288V
At time t = 3 sec,
vc = 120(1 – e -2/15x47 )
vc = 120 (1 – e-2/705 )
= 120 (1 – 0.9976)
= 120 x 0.0024 = 0.288V
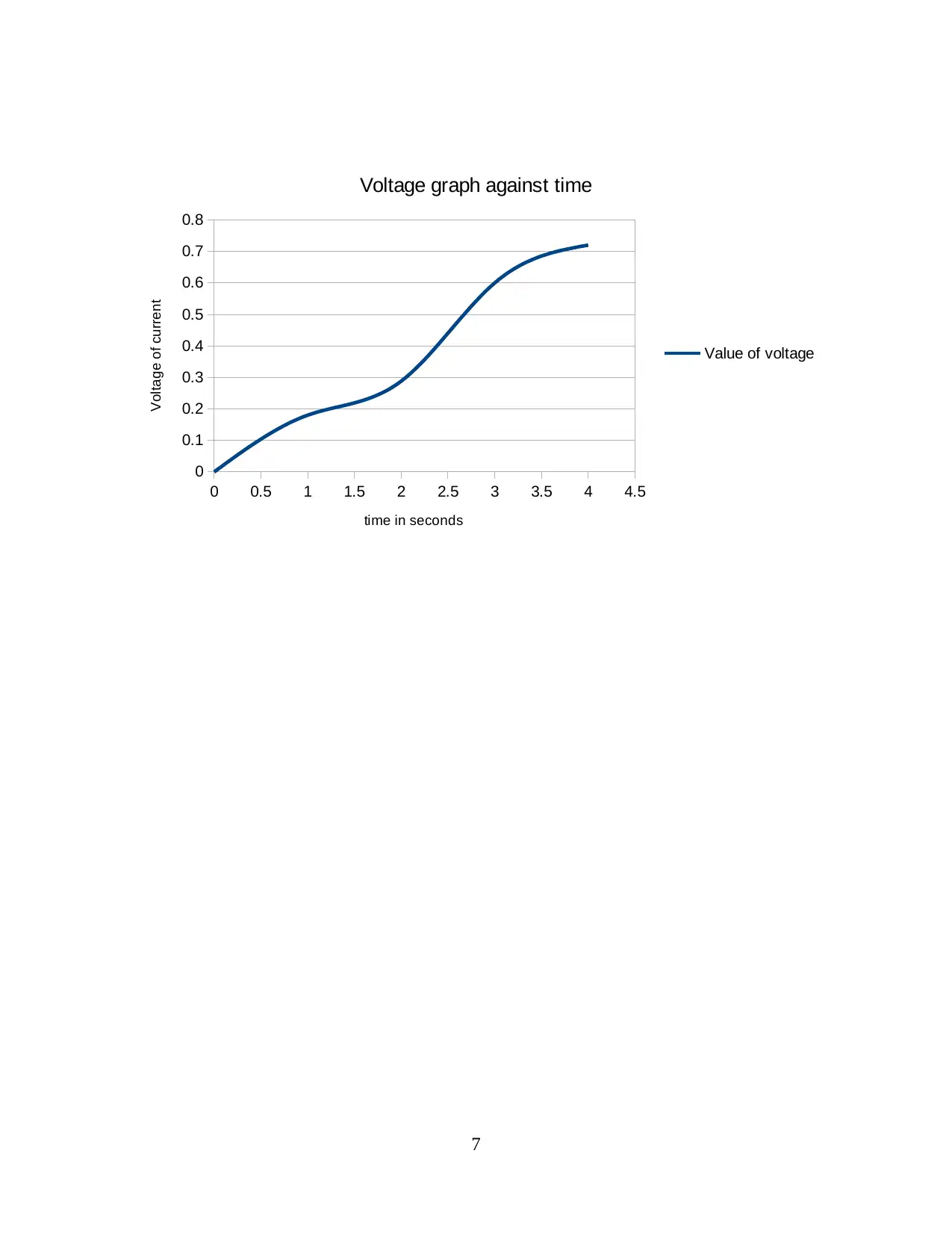
Therefore, at different values of t, voltage can be determined with fixed coulomb charges as
shown in following graph –
Time Value of
voltage
0 sec 0
1 sec 0.18 V
2 sec 0.288 V
3 sec 0.6 V
5

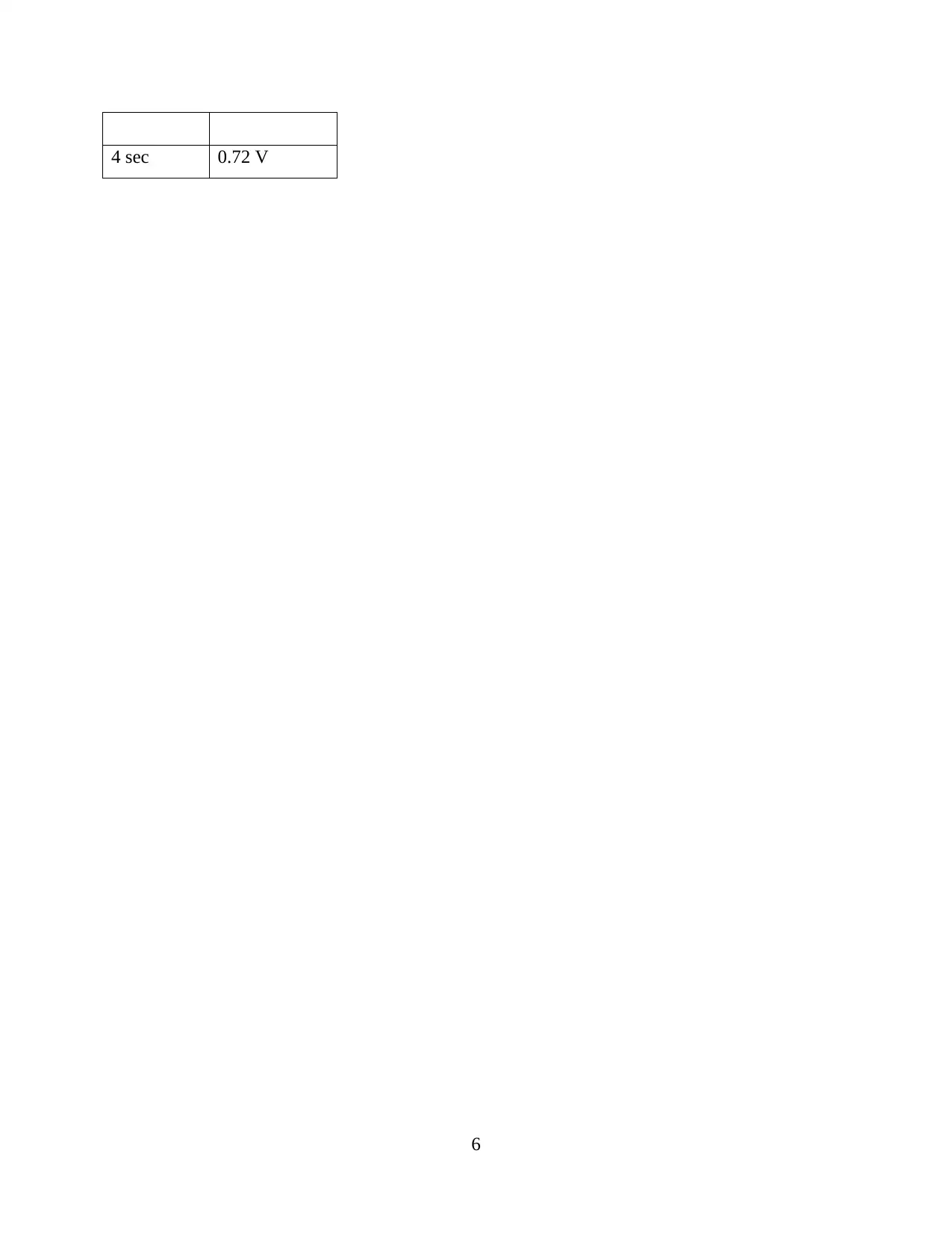
4 sec 0.72 V
6

7
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Voltage graph against time
Value of voltage
time in seconds
Voltage of current

b) Given atmospheric pressure p, altitude
Altitude (h) Pressure (p)
500 73.9
1500 68.42
3000 61.6
5000 53.56
8000 43.41
Where,
p = a. ekh
then, ekh = p/a
or, kh = log p –log a
or, k = 1/h (log p –log a)
at h = 500, p = 73.9
k = 1/500 (log 73.9 – log a)
= 1/500 (1.86 – log a) ….(i)
Similarly, at h = 1500, p = 68.42
k = 1/1500 (log 68.42 – log a)
= 1/1500 (1.83 – log a) …(ii)
Similarly, on solving both equations,
1/500 (1.86 – log a) = 1/1500 (1.83 – log a)
1.86 – log a = 1/3 (1.83 – log a)
Log a = 1.375
Or, a = e1.375 = 3.95
Therefore, k will be = 0.001
8

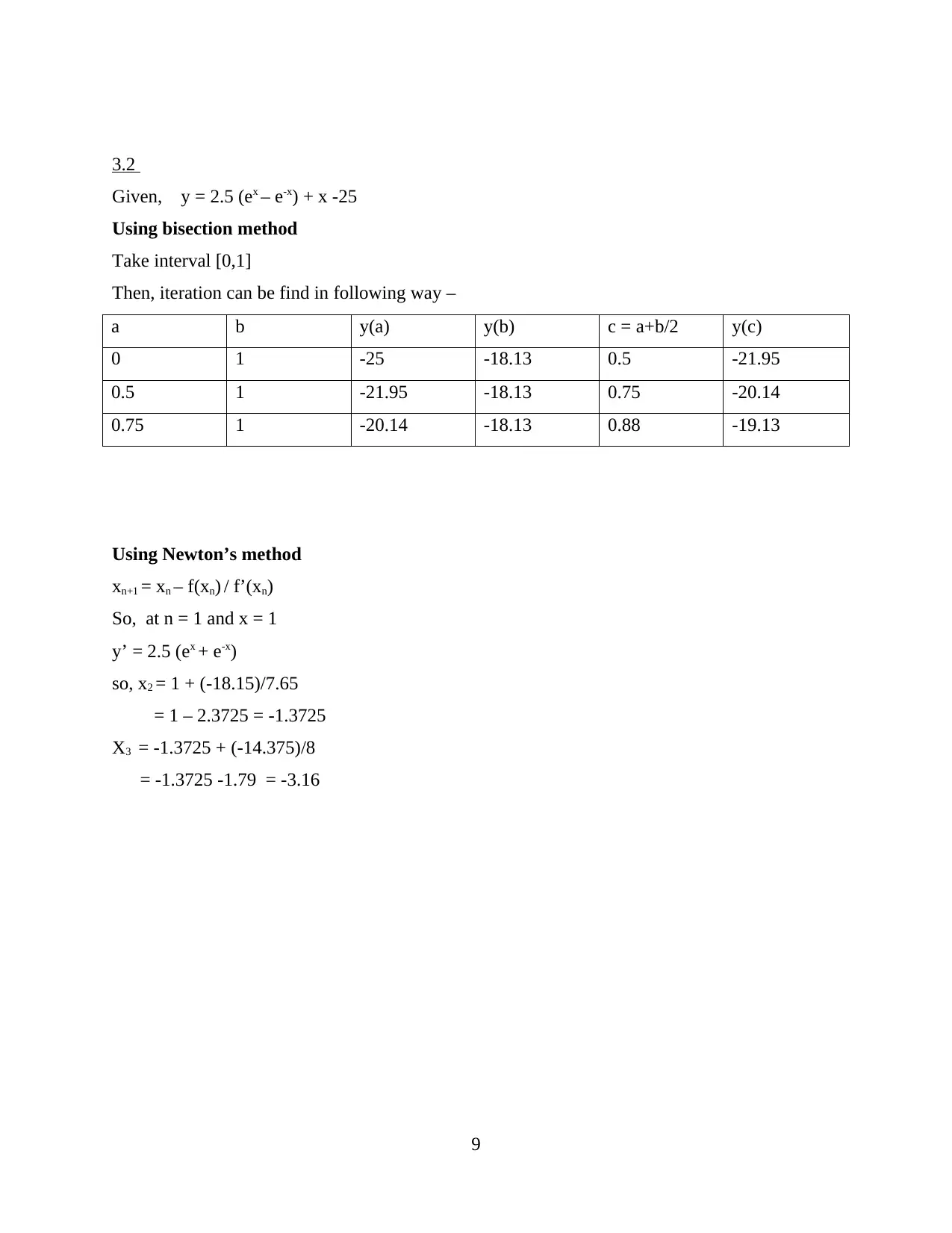
3.2
Given, y = 2.5 (ex – e-x) + x -25
Using bisection method
Take interval [0,1]
Then, iteration can be find in following way –
a b y(a) y(b) c = a+b/2 y(c)
0 1 -25 -18.13 0.5 -21.95
0.5 1 -21.95 -18.13 0.75 -20.14
0.75 1 -20.14 -18.13 0.88 -19.13
Using Newton’s method
xn+1 = xn – f(xn) / f’(xn)
So, at n = 1 and x = 1
y’ = 2.5 (ex + e-x)
so, x2 = 1 + (-18.15)/7.65
= 1 – 2.3725 = -1.3725
X3 = -1.3725 + (-14.375)/8
= -1.3725 -1.79 = -3.16
9

3.4
Mathematical model -
dp = 3(1+t) – p
dt
it can be written as -
p + dp/dt = 3(1+t)
this reflects the first order linear differential equation, as dy/dx + Py = Q
so, it can solve as -
P (I.F) = ∫ Q x I.F dt
here, Integrating Factor (I.F.) = e∫P.dt
in context with given equation, here, P =1, Q = 3(1+t) and I.F. = e∫1.dt = et
so, p. et = ∫ 3(1+t) et .dt
p . et = 3[ ∫et. dt + ∫t.et .dt ]
p . et = 3.et + 3 [ t. ∫ et - ∫ d(t)/dt ∫ et .dt ]
p . et = 3 et + 3 (t -1) et
p . et = 3 et + 3t – 3 et
p = 3 t + e1-t
10

4.21
Differential equation of a LCR circuit is given by
L d2 i/dt2 + R di/dt + 1/C I = 0
on simplifying,
put d i/dt = s
then, equation will transform -
s2 + R/L s + 1/C = 0
s = -R ± √s2 – 4L/C
2L
here, L = 0.1 H, R = 5Ω and C = 20 uF
then, s = -5 ± √52 – 4x 0.1/20
2 x 0.1
s = -5 ± 4.9 = -0.5 and -49.5
0.2
4.20
d2 y/dx2 + 6 dy/dx + 13 y = 0
Let dy/dx = S
then, equation will reduce to
S2 + 6S + 13 = 0
on solving, S = - 3 + 2i < 0
then,
y (x) = e-3x [ C1 cos (2x) + C2 Sin (2x)]
here, C1 and C2 are arbitrary constant,
11

12