Understanding the Formation and Reconstruction of CT Projection Data in Medical Imaging

In this document we will discuss about Understanding the Formation and Reconstruction of CT Projection Data in Medical Imaging and below are the summary points of this document:- Formation of CT Projection Data: Exploring the process of measuring rays in CT and obtaining attenuation coefficients. Reconstruction Steps: Overview of the reconstruction process in CT, including back projection and filtering. CT Numbers: Understanding CT numbers and their relationship to attenuation coefficients in CT imaging.

UNIVERSITY
NAME
ASSIGNMENT
Date

Formation of CT Projection data
Computer Tomography is an essential tool for measuring rays passing through an object and
scattered with the resulting loss given by the equation;
Where the μ is the linear iteration coefficient, x is the distance the x-ray has traveled. X rays
images differ in organs intensity.
The modern CT scanners employ the x-ray fan beam and detector swiping through the patient
offering a thousand projections in various angles. In this case, the distribution of x-rays is of
concern,(Zeng, 2010). The linear attenuation coefficient is obtained through the equation;
Where μ is the attenuation coefficient in 1/cm while the I/Io is the
normalized intensity, length is constantly obtained from ( t Δ)
And steps are taken (Nt).
Reconstruction step
During the reconstruction, a series of attenuation occurs having a function and position level
μ(t,θ). The computer manipulation gives conversion into g(x,y) so as to allow distributions of
attenuation coefficients thus allowing the distribution.
Back projection
The back projection is an elementary process, which is repeated in all angles. The attenuation
coefficient builds up projections passing through the point. The projection does not pass
through perfectly the center (Tahtal et al., 2013), hence the need for description, the nearest
neighbor interpolation is often used to yield the equation;
The t values obtained rare rounded off to a whole number. The
repeated process is done by the equation;

The summation of the matrices is summed and divided by angles number (No).
Filtering
The resultant back projections often yield blurred reconstruction images. Addition of 1/r
convolution to the image is done, hence filtering is applied. Filters to be used can range from
a variety; the simplest method is the ramp filter with the formula;
The filtering method applied has high sensitivity to noise, hence
other filters such as Shepp logan can be used with the formula;
The filter yields less blurred results and less noise sensitivity. These processes of filtering and
back projection process are linear operations. Filtering is initiated through the application of
Fourier transformation, which the resultant is inversed to yield filtered waveform (Tahtali et
al., 2013). The fouries transformations are provided by;
This data is discrete and thus discrete version is applied where the n=t/change in time;
The resultant convolution is converted through the formula;

A
CT Numbers
When both filtering and back projection is completed, the resultant yields two-dimensional
arrays of attenuation coefficients. This is converted into CT numbers rated in Hounsfield
units produced from the formula;
where μ w is water attenuation coefficient.
Objects have a higher density than water offers positive CT scan numbers and objects having
low density than water produce negative CT values (Prun et al., 2013).
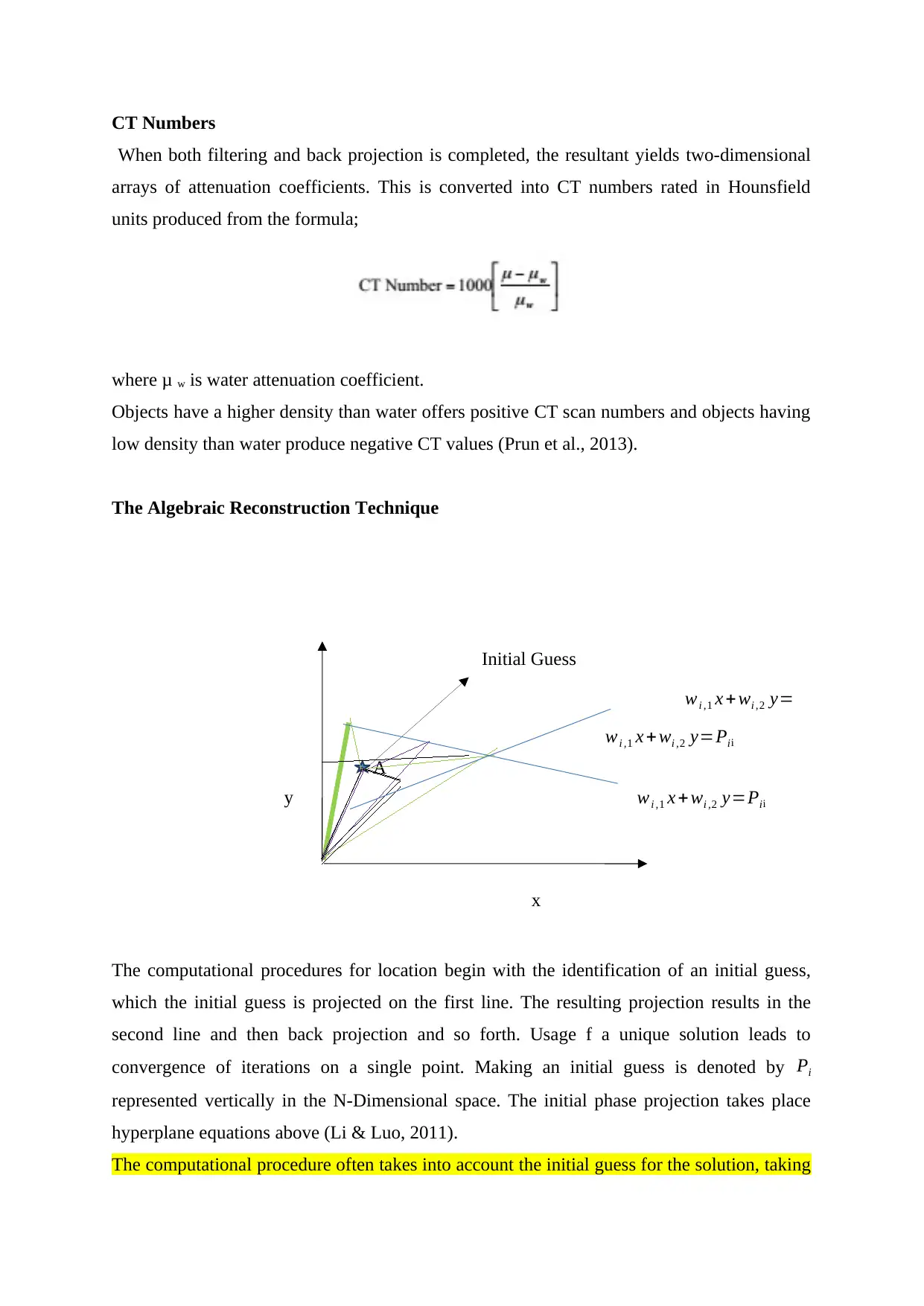
The Algebraic Reconstruction Technique
The computational procedures for location begin with the identification of an initial guess,
which the initial guess is projected on the first line. The resulting projection results in the
second line and then back projection and so forth. Usage f a unique solution leads to
convergence of iterations on a single point. Making an initial guess is denoted by Pi
represented vertically in the N-Dimensional space. The initial phase projection takes place
hyperplane equations above (Li & Luo, 2011).
The computational procedure often takes into account the initial guess for the solution, taking
wi ,1 x + wi ,2 y=Pi
wi ,1 x + wi ,2 y=Pii
Initial Guess
wi ,1 x + wi ,2 y=Pii
x
y

y
successive projections on the hyperplanes. The resultant projections lead to a convergence on
a point. The perpendicular nature of the hyperplanes with the initial guess can possibly arrive
at the correct solution. If there is a small angle in between the hyperplanes, a larger value
may be required before reaching the correct solution. Hyperplane angles influence the
convergence rate of the solution (Zao, Zhao & Zhang, 2015).
The orthogonal hyperplanes made with respect to another offers a correct solution with only a
single pass through the equations. Hence an initial guess of the hyperplanes could lead to an
actual determination of the solution in question. When the M planes are made orthogonal
with respect to each other, the solution is achieved with only one pass. In theory, such
orthogonal assessment s could be arrived through using a procedure such as Gram-Schmidt,
practically it’s not computationally feasible. A study by Chetih & Messali (2015), suggested
a pairwise orthogonal method which is effective in implementation which increases the
overall speed of convergence.
Algebraic Reconstruction Technique wit three projections
In a variable system having three varied hyperplanes, there exist broken lines representing
initial guess. The solution converges at a unique point as illustrated below, thus indicating
oscillating the neighborhood intersections of the hyperplanes.
Where M<N offers a unique solution of a linear equation having infinite solution,
incorporating prior information of the image construction is now possible. The prior image
having ((x,y) offering a non-negative value in each of the solutions, then setting negative
components equal to zero is an option. Inferring the information of (x,y) outside of a certain
area can be done if it is unknown (Geyer et al., 2015).
The projection density allows for throwback reconstruction which modifies the densities
iteratively to achieve reconstructed projection which is in agreement to the measured
A
Initial guesses

projection. Determination of an iterative algorithm converges to a solution which offers
optimal criterion.
The direction which the projections are drawn matters in estimating a solution. The figure
above illustrates three hyperplanes, which needs to establish a shorter distance to be covered
in order to achieve the solution target.
Applications of this are required when large views with larger constructions are implemented,
its difficulty can be associated with calculation, storage, and retrieval of weight coefficient.
Utilization of algebraic expressions is necessary to handle such a case offering different
approximation measures.

References
Chetih, N. and Messali, Z., 2015, May. Tomographic image reconstruction using filtered
back projection (FBP) and algebraic reconstruction technique (ART). In 2015 3rd
International Conference on Control, Engineering & Information Technology (CEIT) (pp. 1-
6). IEEE.
Geyer, L.L., Schoepf, U.J., Meinel, F.G., Nance Jr, J.W., Bastarrika, G., Leipsic, J.A., Paul,
N.S., Rengo, M., Laghi, A. and De Cecco, C.N., 2015. State of the art: iterative CT
reconstruction techniques. Radiology, 276(2), pp.339-357.
Li, X. and Luo, S., 2011. A compressed sensing-based iterative algorithm for CT
reconstruction and its possible application to phase contrast imaging. Biomedical engineering
online, 10(1), p.73.
Prun, V.E., Nikolaev, D.P., Buzmakov, A.V., Chukalina, M.V. and Asadchikov, V.E., 2013.
Effective regularized algebraic reconstruction technique for computed tomography.
Crystallography Reports, 58(7), pp.1063-1066.
Saha, S., Tahtali, M., Lambert, A. and Pickering, M., 2013, March. Novel algebraic
reconstruction technique for faster and finer CT reconstruction. In Fifth International
Conference on Machine Vision (ICMV 2012): Computer Vision, Image Analysis and
Processing (Vol. 8783, p. 878307). International Society for Optics and Photonics.
Tahtali, M., Saha, S.K., Lambert, A.J. and Pickering, M.R., 2013, March. A new imaging
method for real-time 3D x-ray reconstruction. In Medical Imaging 2013: Physics of Medical
Imaging (Vol. 8668, p. 86685G). International Society for Optics and Photonics.
Zeng, G.L., 2010. MRI Reconstruction. In Medical Image Reconstruction (pp. 175-192).
Springer, Berlin, Heidelberg
Zhao, Y., Zhao, X. and Zhang, P., 2015. An extended algebraic reconstruction technique (E-
ART) for dual spectral CT. IEEE transactions on medical imaging, 34(3), pp.761-768.