Center of gravity of the composite cross section of C7x9.8 and S12x35

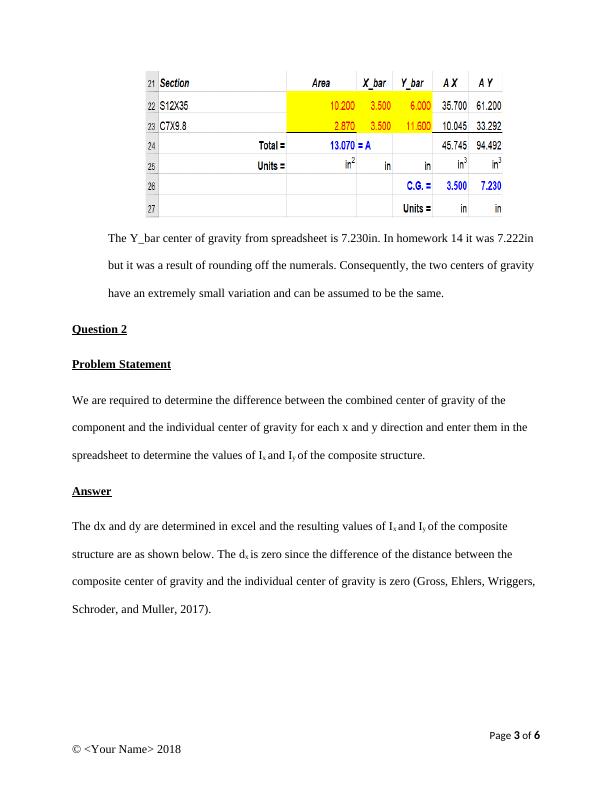
University
Statics
By
Your Name
Date
Page 1 of 6
© <Your Name> 2018

Question1
Problem Statement
We are required to use the sketch of the composite cross section of C7x9.8 and S12x35 and the
spreadsheet provided to calculate the center of gravity of the composite cross-section and
determine how it compares to the manually calculated results in Homework 14.
Answer
To determine the center of gravity using spreadsheet, we follow the following procedure.
Steps
Fill the specific values for C7x9.8 and S12x35 required in the blanks provided in the
spreadsheet.
In the cells requiring the X_bar and Y_bar, we fill the centers of gravity for individual
components from the Y axis and the X axis respectively. Since the composite structure is
symmetrical along the y-axis, the center of X-bar center of gravity, will at the line of
symmetry from the reference point (3.5inches) from the reference. The Y_bar for the
C7X9.8 channel is 11.6inches while that of the S12x35 beam is at 6.00inches. Filling the
data into the spreadsheet produces a Y-bar center of gravity of the composite structure
equal to 7.230 and X-bar center of gravity equal to 3.5inches as shown below.
Page 2 of 6
© <Your Name> 2018

The Y_bar center of gravity from spreadsheet is 7.230in. In homework 14 it was 7.222in
but it was a result of rounding off the numerals. Consequently, the two centers of gravity
have an extremely small variation and can be assumed to be the same.
Question 2
Problem Statement
We are required to determine the difference between the combined center of gravity of the
component and the individual center of gravity for each x and y direction and enter them in the
spreadsheet to determine the values of Ix and Iy of the composite structure.
Answer
The dx and dy are determined in excel and the resulting values of Ix and Iy of the composite
structure are as shown below. The dx is zero since the difference of the distance between the
composite center of gravity and the individual center of gravity is zero (Gross, Ehlers, Wriggers,
Schroder, and Muller, 2017).
Page 3 of 6
© <Your Name> 2018