Quarter Car Modelling Assignment

This assignment focuses on quarter car modelling for automotive dynamics and safety. It includes tasks such as performing free body diagrams, finding equations of motion, comparing free and forced vibrations, and simulating the system using MATLAB. The assignment also explores the suspension's function on various road profiles.

UNIVERSITYOF HERTFORDSHIRE
School of Engineering and Technology
7AAD0054 - Automotive dynamics and safety
Quarter Car Modelling
Assignment
Student Name
Student Registration Number
Date of submission
Page 1 of 8

UNIVERSITYOF HERTFORDSHIRE
School of Engineering and Technology
Tasks
The quarter car model has been used by the automotive researchers to study the dynamics of a vehicle
during the design phase. The model examines the dynamics of the vehicle focusing on one wheel
section over different road surfaces during transmission. The software used in the simulation of
Newton’s second law of motion is MATLAB R2018b software. The simulation discusses the
suspension based on different damping coefficients as determined in the system payload as well as the
car speed.
Task 1 (3 marks)
Perform free body diagram (FBD) for the system to satisfy the Newton’s 2nd low. Please develop your
own assumptions and provide/plot a clear evaluation on applied forces to the identified masses.
SOLUTION
The quarter car model is a combination of a single wheel with two degree of freedom. The following
is a physical model of the quarter car model,
The free body diagram alongside the physical vehicle wheel representation is as illustrated below,
Page 2 of 8

UNIVERSITYOF HERTFORDSHIRE
School of Engineering and Technology
Assumptions:
(i) The quarter car model is a representation of the entire vehicle in the analysis of the active
suspension and system dynamics.
(ii) The damper has two or more opted damping rates that require a high force at low
velocities and a low force at high velocities and can move quite swiftly among the two.
Task 2 (3 marks)
Find the equation of motions and response of the system to oscillations. You may use your own
assumptions as used in the FBD of the system. Please make sure to address loading scenarios applied
to masses, springs and damping elements. Please consider any external forces applied to the system.
SOLUTION
ms ¨Z s=−bs ( ˙Zs − ˙Zu ) −ks ( Zs−Zu ) +f a
mu ¨Zu=bs ( ˙Z s− ˙Zu ) +ks ( Z s−Zu ) −f a +bt ( ˙Zr− ˙Zu ) +k t ( Zt −Zu )
Task 3 (3 marks)
Please consider both free and forced vibration and compare the results. The assumption made in
previous tasks can be used here. However, your defined assumptions should be based on clear and
specific metrics which you may use to assess these solutions.
To obtain the undamped natural frequencies of the unperturbed system, the damper parameters and
forces are equated to zero such that,
Page 3 of 8

UNIVERSITYOF HERTFORDSHIRE
School of Engineering and Technology
ms ¨Z s=−0 ( ˙Zs− ˙Zu )−ks ( Zs −Zu ) +0
mu ¨Zu=0 ( ˙Zs− ˙Zu ) +k s ( Zs −Zu )−0+0 ( ˙Zr− ˙Zu )+kt ( Zt−Zu )
ms ¨Z s=−k s (Z s−Zu )
mu ¨Zu=ks ( Zs −Zu ) +kt ( Zt −Zu )
ms ¨Z s+ ks ( Zs−Zu ) =0
mu ¨Zu +k s ( Zu−Zs ) +kt ( Zu−Zt ) =0
The solutions can be written as,
Zs=zs ewt , Zu =zu ewt
[ A ] [ z ] = [ −ms w2 +k s −ks
ks −mu w2 +ks +ku ] [ zs
zu ]
The stiffness matrix of the system is given as A. The matrix determinant is obtained as,
det A=¿ ms mu w4 −ms ( k s+ ku +mu ks ) w2+ks ku ¿
For the purpose of design optimization, the James principle and RMS of the sprung mass acceleration
is given as,
|Z1|
|q| =[ ( 1−λ2 ) 2
+ 4 ξ2 λ2
Δ ]0.5
Δ= [ (1− ( ω
ω0 )2
(1+ γ− 1
μ ( ω
ω0 )2
−1 )) ]2
+4 ξ2
( ω
ω0 )2
[γ −( 1
μ +1 ) ( ω
ω0 )2
]
γ= K t
Ks
, μ= ms
mt
, ω0= √ k
ms
, ξ= C
2 √ ms k
Considering the road excitation and the sprung mass acceleration,
Task 4 (3 marks)
Please simulate the system using a MATLAB program. You can consider the assumption made in
previous tasks and use the supportive information provided for this assignment on the Canvas. These
should lead you to develop your own Simulink model with a potential design choice which can be
assessed against the model derived in previous tasks.
SOLUTION
The system payload parameters are given as,
Page 4 of 8

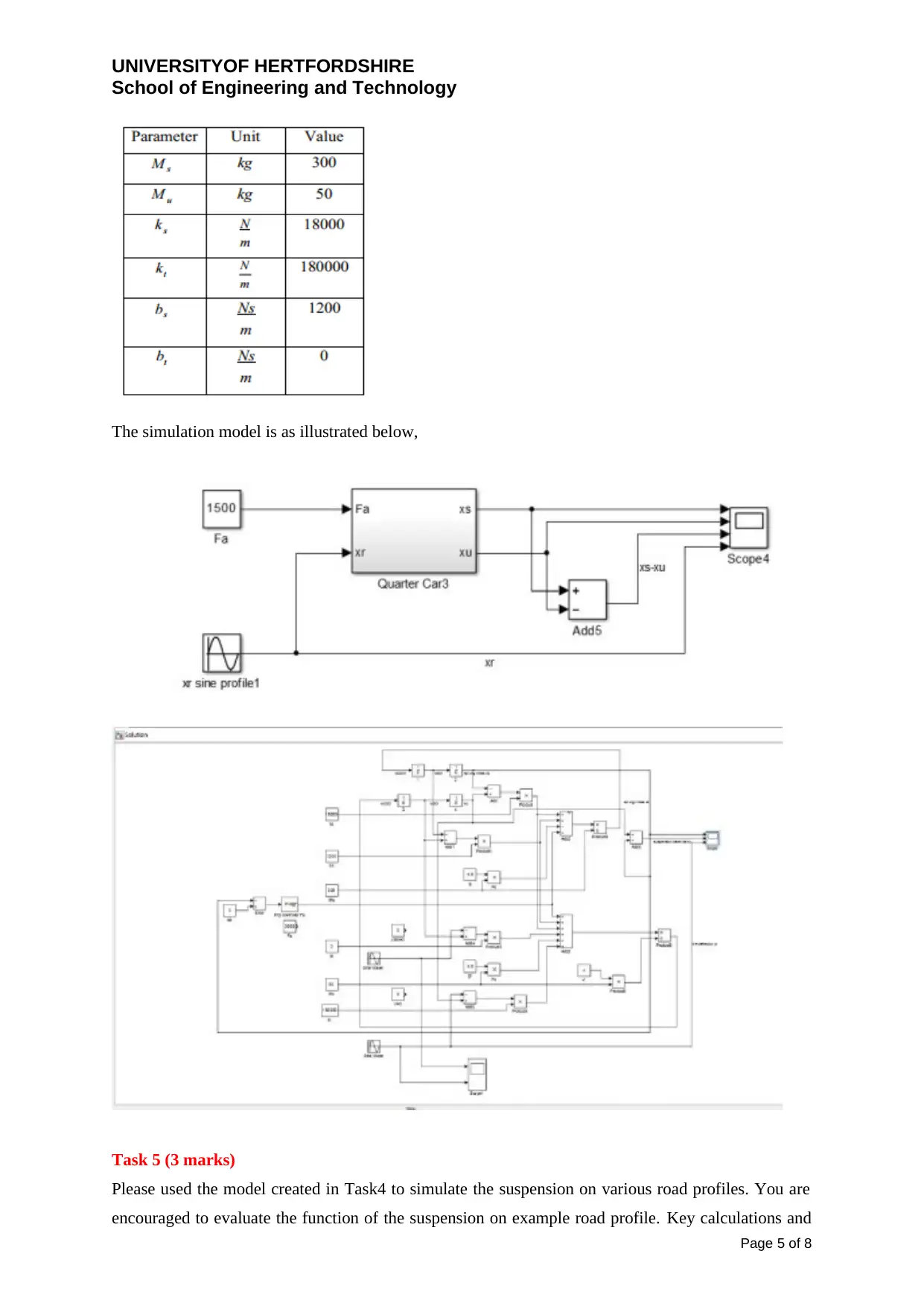
UNIVERSITYOF HERTFORDSHIRE
School of Engineering and Technology
The simulation model is as illustrated below,
Task 5 (3 marks)
Please used the model created in Task4 to simulate the suspension on various road profiles. You are
encouraged to evaluate the function of the suspension on example road profile. Key calculations and
Page 5 of 8

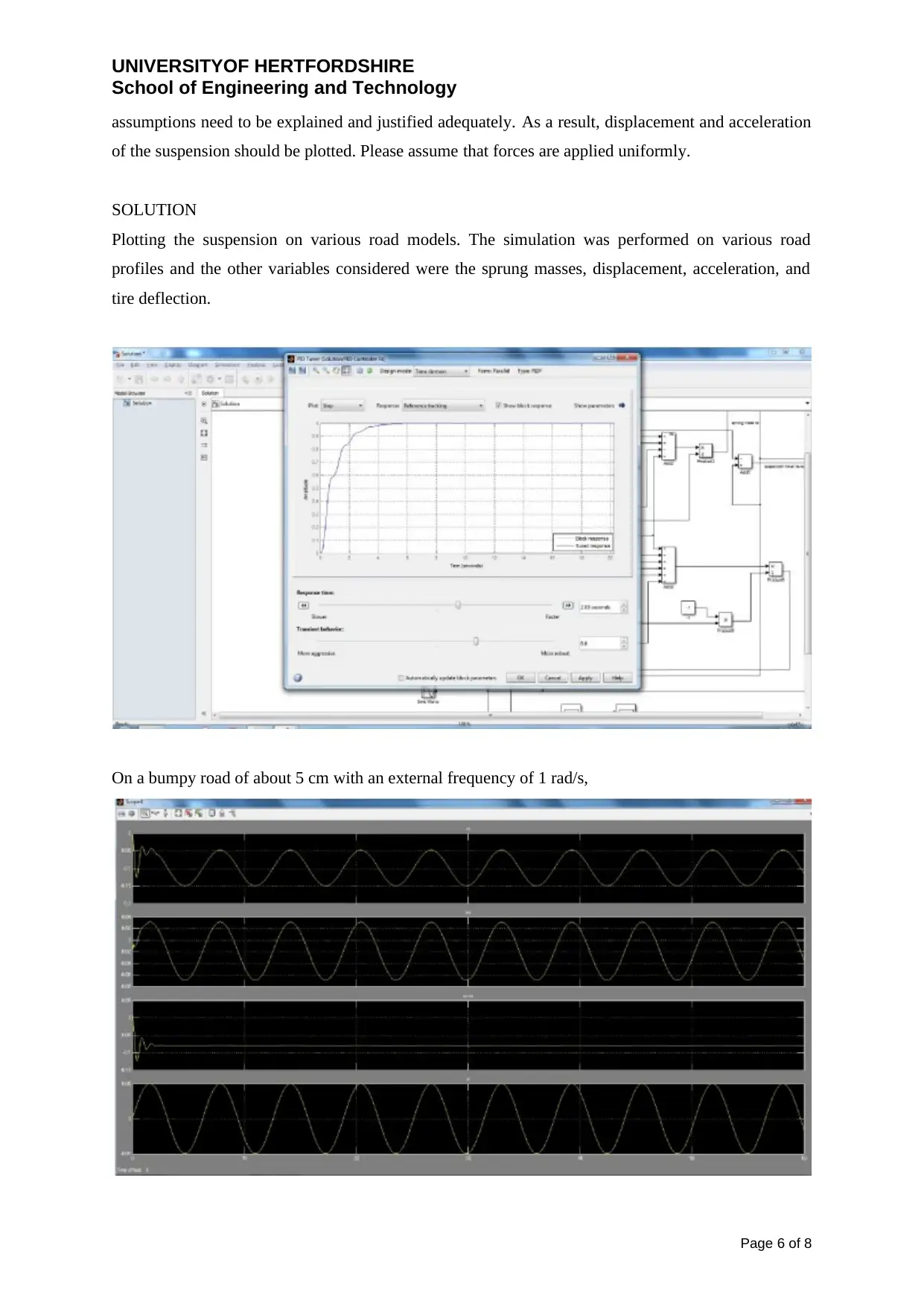
UNIVERSITYOF HERTFORDSHIRE
School of Engineering and Technology
assumptions need to be explained and justified adequately. As a result, displacement and acceleration
of the suspension should be plotted. Please assume that forces are applied uniformly.
SOLUTION
Plotting the suspension on various road models. The simulation was performed on various road
profiles and the other variables considered were the sprung masses, displacement, acceleration, and
tire deflection.
On a bumpy road of about 5 cm with an external frequency of 1 rad/s,
Page 6 of 8

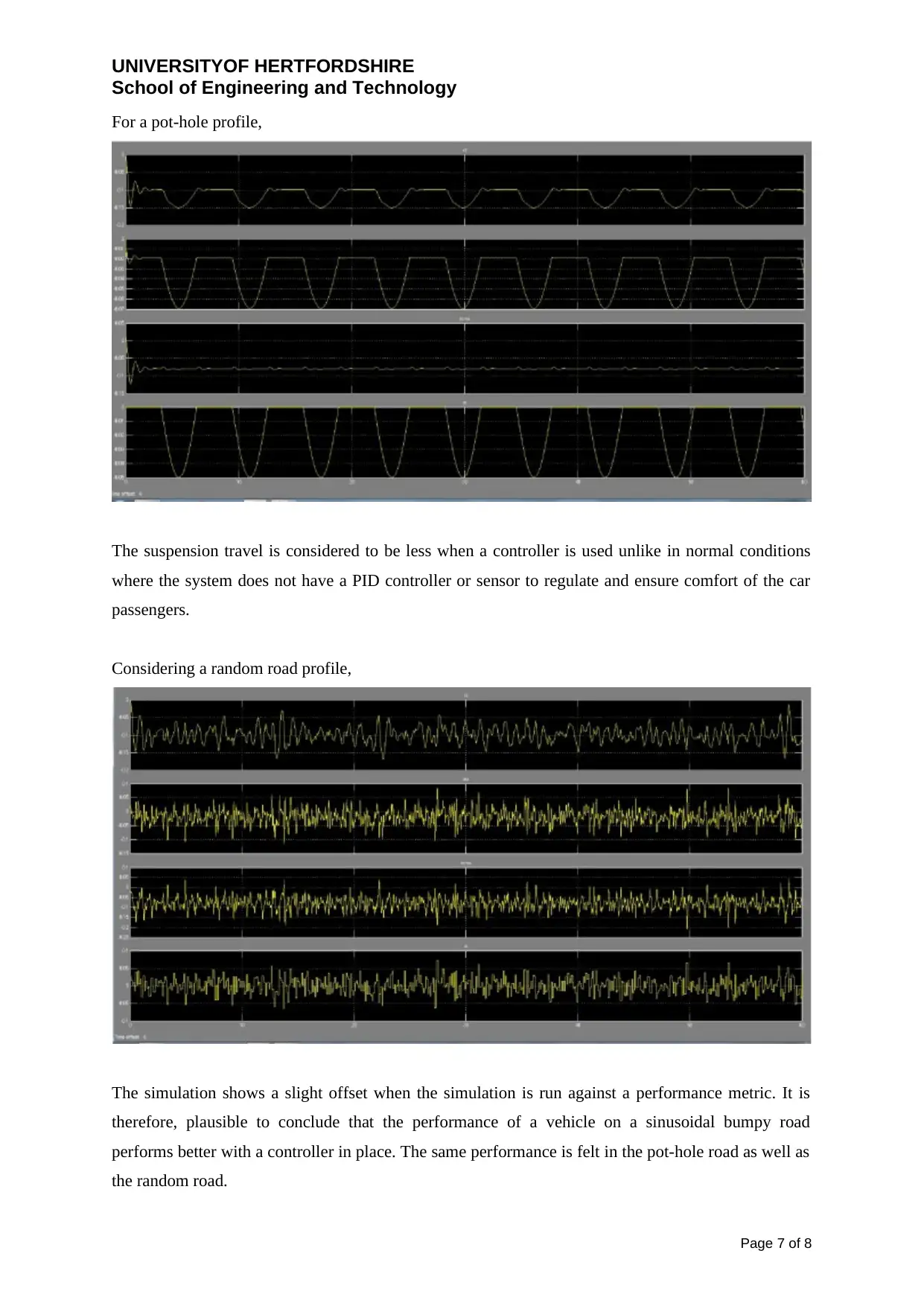
UNIVERSITYOF HERTFORDSHIRE
School of Engineering and Technology
For a pot-hole profile,
The suspension travel is considered to be less when a controller is used unlike in normal conditions
where the system does not have a PID controller or sensor to regulate and ensure comfort of the car
passengers.
Considering a random road profile,
The simulation shows a slight offset when the simulation is run against a performance metric. It is
therefore, plausible to conclude that the performance of a vehicle on a sinusoidal bumpy road
performs better with a controller in place. The same performance is felt in the pot-hole road as well as
the random road.
Page 7 of 8

UNIVERSITYOF HERTFORDSHIRE
School of Engineering and Technology
REFERENCES
[1] Inman D J 2001 Engineering Vibration 2nd ed. Prentice Hall International Inc. New
Jersey.
[2] Rao S S 2004 Mechanical Vibrations 4th ed. Pearson/Prentice Hall Upper Saddle
River New Jersey.
[3] Markel T, Brooker A, Hendricks T, Johnson V, Kelly K, Kramer B, O’Keefe M, Sprik
S and Wipke K 2002 ADVISOR : a systems analysis tool for advanced vehicle
modeling J. of Power Sources pp 255-266.
[4] Griffiths K R 2012 An Improved Method for Simulation of Vehicle Vibration Using a
Journey Database and Wavelet Analysis for the Pre- Distribution Testing of Packaging
(Doctoral dissertation) retrieved from
opus.bath.ac.uk/38300/1/UnivBath_PhD_2012_K_Griffiths.pdf
[5] Phalke T P and Mitra A C 2017 Analysis of ride comfort and road holding of quarter
car model by Simulink Materials Today : Proc. 4 pp 2425-2430.
[6] Talukdar R P and Talukdar S 2016 Dynamic analysis of high speed maglev vehicle-
guideway system using Simulink Procedia Engineering 144 pp 1094-1101.
Page 8 of 8