Using Numeracy Data & IT

This article discusses arithmetic competence, IT competence, and numeracy concepts with solved questions and exercises. It covers topics such as fractions, percentages, discounts, and Olympic Games medal tables. The article also includes instructions on how to perform various Microsoft Office activities. Subject: Numeracy Data & IT, Course Code: FP, College/University: Not mentioned.

Using numeracy data
and IT FP

Contents
Contents...........................................................................................................................................2
INTRODUCTION...........................................................................................................................3
Part 1................................................................................................................................................3
Question 1....................................................................................................................................3
Question 2....................................................................................................................................4
Question 3....................................................................................................................................4
Question 4....................................................................................................................................4
Question 5....................................................................................................................................5
Question 6....................................................................................................................................5
Question 7....................................................................................................................................6
Question 8....................................................................................................................................6
Question 9....................................................................................................................................6
Question 10..................................................................................................................................7
Part 2................................................................................................................................................7
Part 3..............................................................................................................................................10
Question 13................................................................................................................................12
Question 14................................................................................................................................13
Question 15................................................................................................................................14
Question 16..................................................................................................................................1
Olympic Games Medal Table..........................................................................................................2
Olympic Games Medal Tables........................................................................................................3
Conclusion.......................................................................................................................................4
References........................................................................................................................................5

INTRODUCTION
Arithmetic competence is described as the ability to conceive about and apply accurate
theoretical concepts, while IT competence is described as having the ability to compute and
evaluate the available arithmetic and IT data (Bertheussen, 2016). Comprehending basic
arithmetic operations such as divides, multiplication, addition, and subtraction is an important
aspect of developing fundamental mathematical knowledge. Mathematics is required for
reasonable cognition and learning function in everyday routines. The concept of numeracy is
important for actions like consuming, following instructions, assessing invoicing, and playing. It
also makes concepts of math, patterns, scheduling, and forms available. It was established that
the concepts of literature and arithmetic may enable people to build the fundamental skills
individuals require to thrive in life. There is a comprehensive plan for increasing literacy and
mathematical abilities, and also supporting students in living a joyful and fulfilling life and
contributing as an active and well-informed community. This mathematics curriculum is broken
into three main exercises; each of them must be typically performed.
Part 1
Question 1
As already stated, mathematics competency is interpreted as the capability to analyse and
implement simple arithmetic concepts. Fundamental reasoning skills necessitate knowledge of
fundamental arithmetic computation such as dividing, multiplication, combining, and removing.
Further below, the numerator and denominator ideas will be discussed (Bulteau, Feuillet and
Dantan, 2019).
Numerator: The partial digits formula is a/b, in which a represents the numerator and b
represents the denominator. For example, 4/5 is a %, and the lines between the numerals 4 and 5
are a proportion bar pair. As a consequence, the denominator is the amount underneath the %
line, while the numerator is the amount from above. The fraction is represented in the diagram
underneath.-

Denominator: The least number in a percentage that indicates the number of comparable
components split into an item is the denominator (Chomicki, Schaefer and Renner, 2020).
Question 2
Expressing 24/40 and 18/42 in their simplest forms
3 ∧18
24 = 5 = 3
40 42 7
Question 3
(a) , Expressing the fraction 2/3, ¾ and 5/6 as equivalent fractions with a denominator of 12.
2 = 8 , 3 = 9 5 = 10
3 12 4 12 6 12
(b)
Total books in library = 60000
Books on subject of business = 14000
Healthcare books = 22000
Psychology and law books = 12000
Remaining books = 60000 – 14000 + 22000 + 12000
= 60000 – 48000
= 12000
Calculate computing books which is 2/3 of remaining books = 12000*2/3 = 8000
Computing books in percentage = 8000/60000*100 = 13.33%
Question 4
Total money given by Liz = £50 × 3 = £150
Total price of 2 pairs of shoes = £150 - £10.50
= £139.50
Price of each pair of shoes = £139.50/2
= £69.75 per pair
Question 5
(a). 240.50 x 19.54 (2 significant)
The two digits have a maximum of 4 decimal places in the given statement. 24050 x 1954 =
46993700

240.50 x 19.54 = 4699. 3700
= 4699.37 (2 decimal places)
(b) Rewriting 52100 to the power of 10
5.21 x 104
Question 6
(a)
Discount rate = 30%
No of people = 3
Total amount paid = £210
Amount paid for one person = £210/3 = 70
Percentage of amount paid = 70%
Let the original amount for one person = x
70 = 70/x *100
X = 100
Then original amount for 3 person = 3 * 100 = £300
Total saving = original amount – amount paid
= £300 – £210
=£ 90
(b) The total amount saved was £90. Because there are three people participating, the mean costs
per person may be computed as £90/3 = £30
Question 7
(a). ¾ - 7/9 + 2/3
(27-28+24)/36 = 23/36
(b)
Since the considerable number 1 is at the tenth position, the biggest position that after decimal
point, the greatest amount is 0.1 (Danial, Feldman and Hutterer, 2019).
Question 8
Men = 90

Women = 6.
Women who said yes = 3/10
Altogether said yes = 3/5
Total number of people said yes = (90 + 60)
= 90
Total number of women said yes = 60
= 18
Total number of man said yes = 90 – 18
= 72
Number of man said no = 90 -72 = 18
Percentage of the men said no =
= 20%
Question 9
- Annabelle is a Londoner who resides in Bermondsey.
-She is scheduled to speak at 10:30 a.m. in Birmingham.
-Getting from her residence to Train Stations, where she takes the train to Birmingham, could
require her an hour (1 hour).
-The train ride from Euston Station to Birmingham takes one hour and ten minutes (7/6 hours).
- The meeting location The metro in Birmingham is a 5-minute (1/6-hour) walk away.
As a result, Annabelle's overall commute time from her home to the meeting spot is = 1 hr +
7/6 hr + 1/12 hr = 27/12 hr = 2 hours 15 minutes.
To determine the time, divide the entire time required to arrive to the conference site by the
planned time: (10 hours 30 minutes) – (2 hours 15 minutes) = 8 hours 15 minutes.
Despite the fact that the trains from Euston to Birmingham arrives at 5 minutes after the hour, 25
minutes after the hour, and 45 minutes after the 60 minutes.
As a result, Annabelle can walk out of the house no later than 8:15 a.m.

Question 10
Weight of Shredded Wheat = 0.35 kg
A box of Weetabix weighs = 9/25 kg = 0.36 kg
Therefore, 0.36 Kg or 9/25 Kg is heavier than 0.35Kg of Shredded Wheat.
Part 2
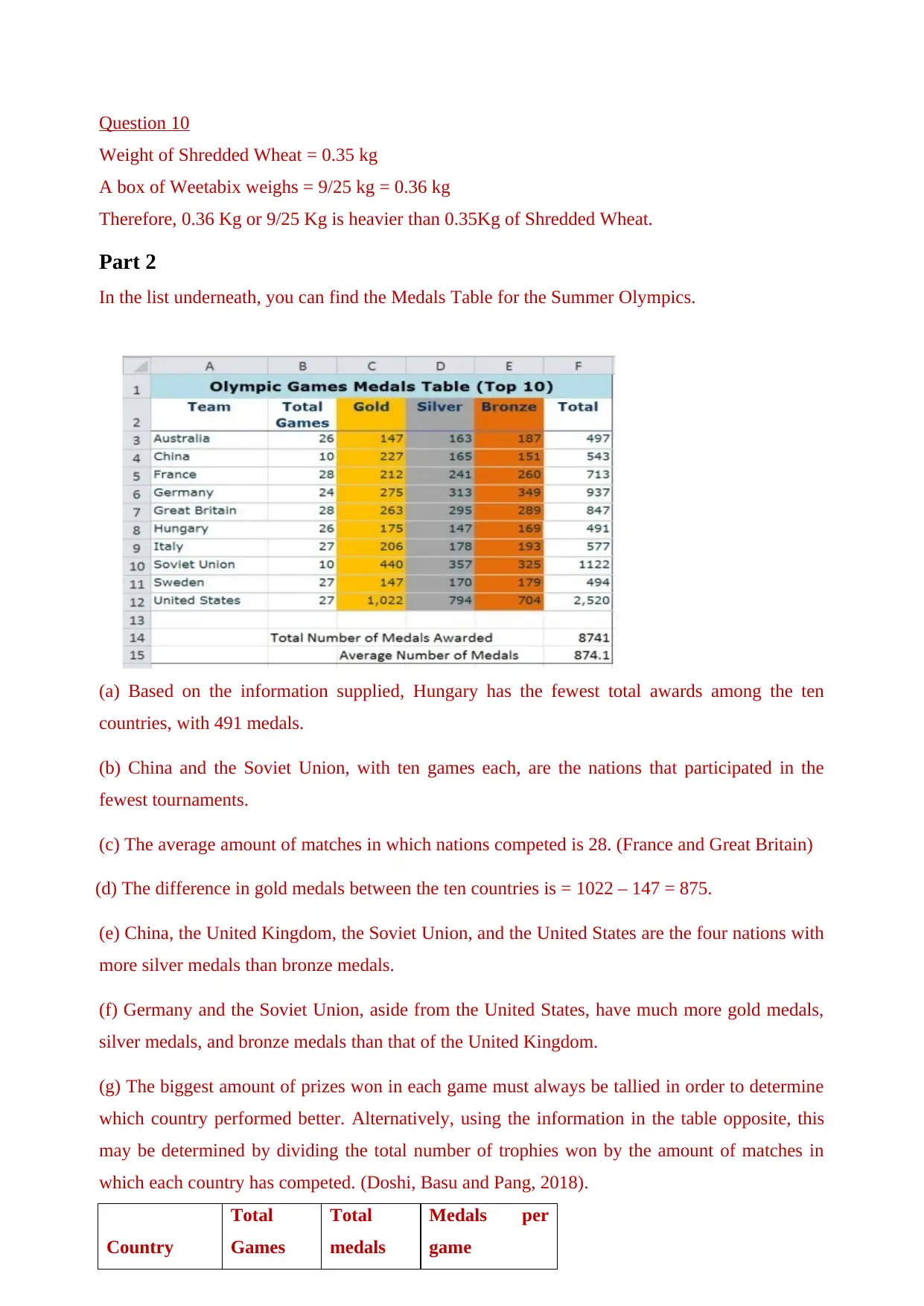
In the list underneath, you can find the Medals Table for the Summer Olympics.
(a) Based on the information supplied, Hungary has the fewest total awards among the ten
countries, with 491 medals.
(b) China and the Soviet Union, with ten games each, are the nations that participated in the
fewest tournaments.
(c) The average amount of matches in which nations competed is 28. (France and Great Britain)
(d) The difference in gold medals between the ten countries is = 1022 – 147 = 875.
(e) China, the United Kingdom, the Soviet Union, and the United States are the four nations with
more silver medals than bronze medals.
(f) Germany and the Soviet Union, aside from the United States, have much more gold medals,
silver medals, and bronze medals than that of the United Kingdom.
(g) The biggest amount of prizes won in each game must always be tallied in order to determine
which country performed better. Alternatively, using the information in the table opposite, this
may be determined by dividing the total number of trophies won by the amount of matches in
which each country has competed. (Doshi, Basu and Pang, 2018).
Country
Total
Games
Total
medals
Medals per
game

Australia 26 497 19.11538462
China 10 543 54.3
France 28 713 25.46428571
Germany 24 937 39.04166667
Great Britain 28 847 30.25
Hungary 26 491 18.88461538
Italy 27 577 21.37037037
Soviet Union 10 1122 112.2
Sweden 27 494 18.2962963
United States 27 2520 93.33333333
Depending on the statistics provided, it is clear that the Soviet Union is the country that plays
the best, as seen by the fact that they receive one of most prizes every game. (112.2 medals per
game).
(b) There could have been a number of reasons why a country such Jamaica, which would be
known for its sportsmen, does not position in the top ten. The main reason for their absence of
engagement in many competitions could very well be owing to their small population in
contrast to other countries. The more populous a country is, the more probable it is to compete
in more competitions and, as a consequence, to place among some of the top ten champion
countries. Moreover, in comparison to other disciplines including collective athletics, in which
patients rarely participate, the physiological tasks performed in Olympic competitions are small
(Espinosa-Oviedo, 2020).
(i) As per the table, the Soviet Union is the closest competitor to the United States, hence every
medal category in the United States will indeed be compared to that of the Soviet Union.
Gold medal US = 1022
Soviet Union = 440
The difference = 1022 – 440 = 582
Silver medal US = 794
Soviet Union = 357
The difference = 794 – 357 = 437
Bronze medal
US = 704
Soviet Union = 325

The difference = 704 – 325 = 379
According to the calculations provided, the gold medal division is the one where the United
States considerably surpassed its nearest opponent, the Soviet Union.
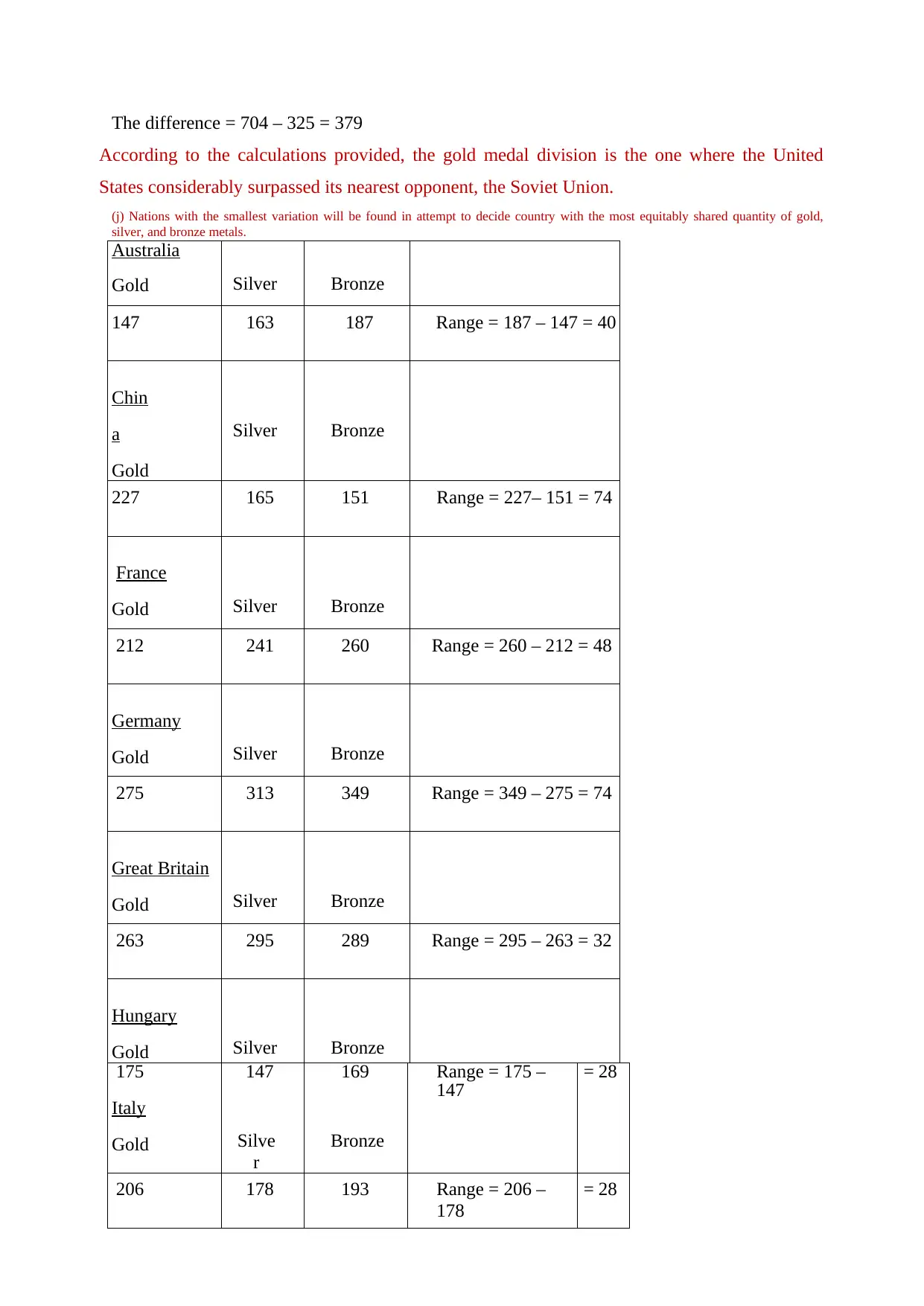
(j) Nations with the smallest variation will be found in attempt to decide country with the most equitably shared quantity of gold,
silver, and bronze metals.
Australia
Gold Silver Bronze
147 163 187 Range = 187 – 147 = 40
Chin
a
Gold
Silver Bronze
227 165 151 Range = 227– 151 = 74
France
Gold Silver Bronze
212 241 260 Range = 260 – 212 = 48
Germany
Gold Silver Bronze
275 313 349 Range = 349 – 275 = 74
Great Britain
Gold Silver Bronze
263 295 289 Range = 295 – 263 = 32
Hungary
Gold Silver Bronze
175
Italy
Gold
147
Silve
r
169
Bronze
Range = 175 –
147 = 28
206 178 193 Range = 206 –
178
= 28

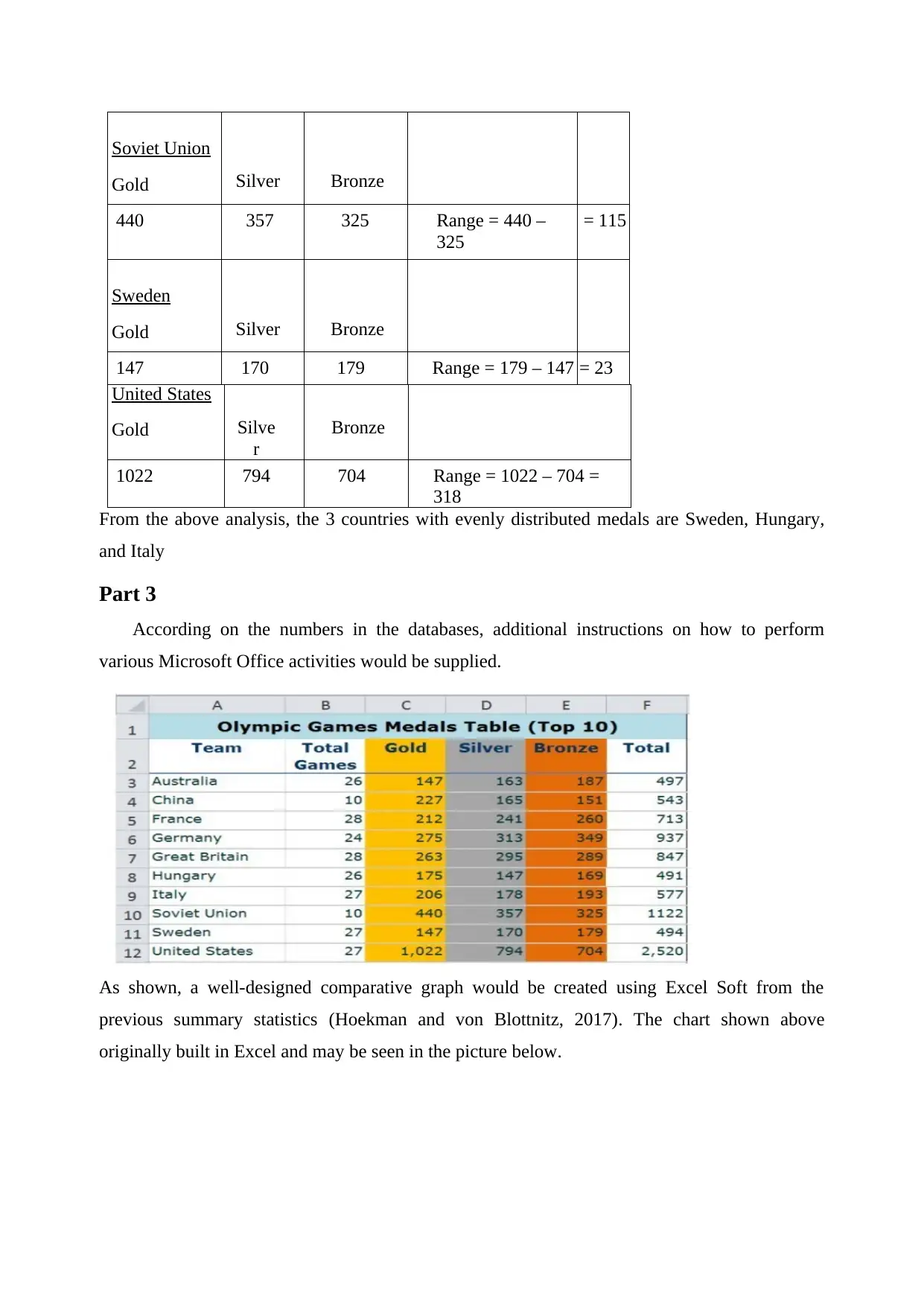
Soviet Union
Gold Silver Bronze
440 357 325 Range = 440 –
325
= 115
Sweden
Gold Silver Bronze
147 170 179 Range = 179 – 147 = 23
United States
Gold Silve
r
Bronze
1022 794 704 Range = 1022 – 704 =
318
From the above analysis, the 3 countries with evenly distributed medals are Sweden, Hungary,
and Italy
Part 3
According on the numbers in the databases, additional instructions on how to perform
various Microsoft Office activities would be supplied.
As shown, a well-designed comparative graph would be created using Excel Soft from the
previous summary statistics (Hoekman and von Blottnitz, 2017). The chart shown above
originally built in Excel and may be seen in the picture below.

To emphasise the area shown in the provided information, the emphasizing choice would also
have been selected and the appropriate element selected, as seen in the following image.
The completed table, complete with all of its vital elements, is then shown and discussed in the
figure below (Jones and Panova, 2018).

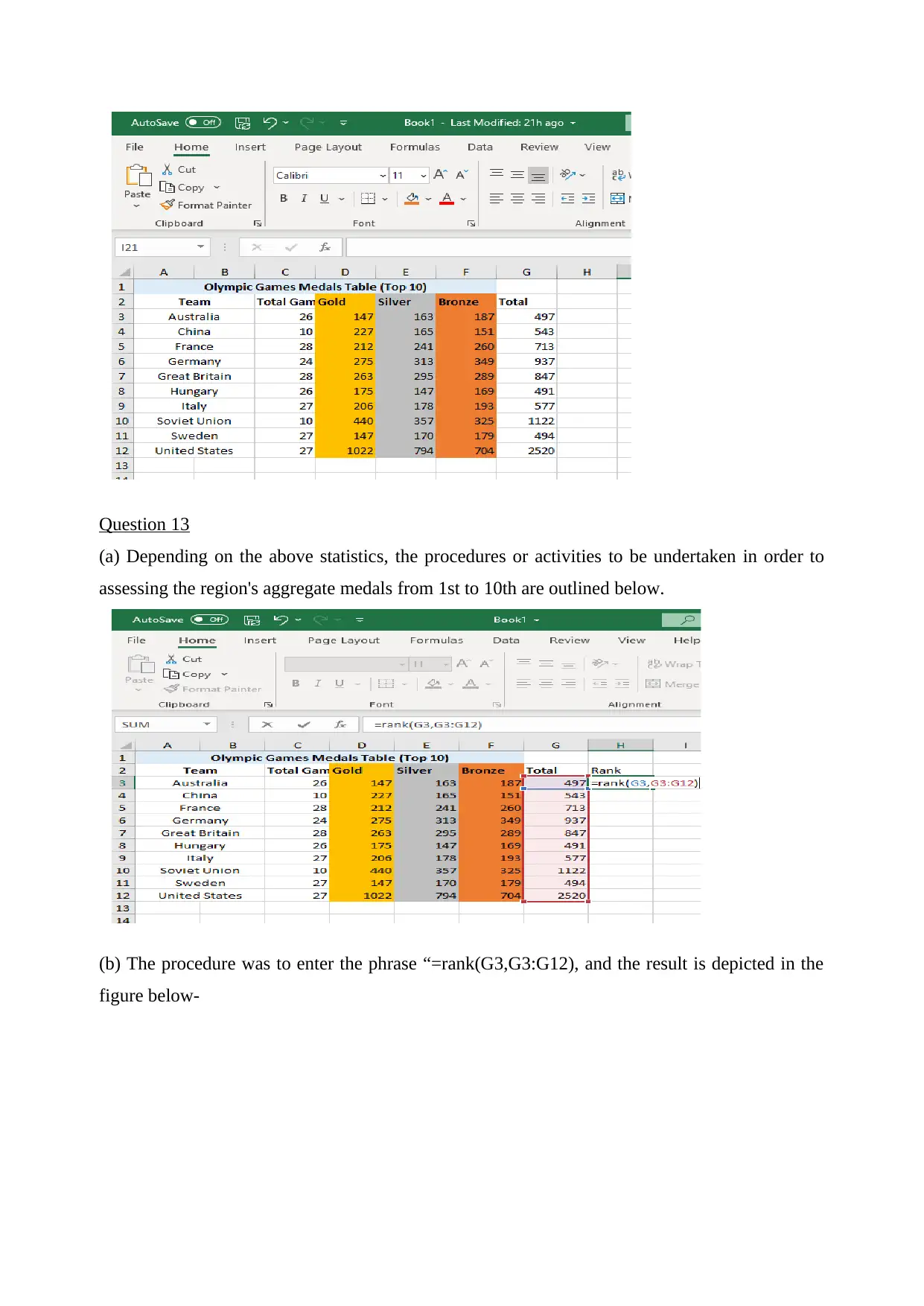
Question 13
(a) Depending on the above statistics, the procedures or activities to be undertaken in order to
assessing the region's aggregate medals from 1st to 10th are outlined below.
(b) The procedure was to enter the phrase “=rank(G3,G3:G12), and the result is depicted in the
figure below-

(c) The stacked bar diagram is the graphical representation of data that would suffice or be
suitable for displaying exclusively gold medals.
(d) The paragraphs "Team" and "Total" are the portions that really should be copied (Naimipour,
Guzdial and Shreiner, 2020).
(e) The overall number of awards earned can be calculated using Excel's "SUM(G3:G12)"
function, as illustrated in the picture below.
Question 14
(a) As shown in the image below, the total number of medals for Germany and the United
Kingdom can indeed be calculated using Excel's "Sum (G6 and G7)" formula.
(b) The method shown in the figure below could also be utilized to calculate the total average
number of silver medals won by all European countries (Nitu, Coelho and Madiraju, 2021).

(c) For countries that already have participated in fewer than 20 championships, the technique
depicted in the figure below has been used to calculate cumulative gold medals.
(d) In the freshly developed Excel Spread Sheet, the researching and finding procedures
would've been utilized to discover Italy and its related medals tally. However, the approach to
employ is "=Find(A9:G9)." The following figure depicts the elaboration:
Question 15
(a) > The method could then be employed to determine the median number of medals for each
medal class, and the results are depicted in the graphic below.
The method “=median (D3:D12)” is used to compute the median for a gold medal, as seen in
the figure beneath.

As illustrated in the image below, the median for the Silver medal is computed utilizing the
equation "=median (E3:E12)."
The method “=median (F3:F12)” is used to compute the median for a Bronze medal, as seen in
the image below.
(b) The algorithm may have been employed to determine the average frequency of prizes
awarded in each medal class, and the results are depicted in the figure below.
The mean for the Gold medal is calculated using the formula “=Average (D3:D12),” as
depicted in the figure below.

As illustrated in the figure, the mean for the Silver medal is determined using the calculation
"=Average (E3:E12)."
The Bronze medal's mean is calculated using the technique "=Average (F3:F12)," as seen in the
graphic below.
(c) The mean of the collection obtained would've been computed first, following sources, as
well as the standard deviation of the data provided.
Mean = Total outcome/ number of outcome (N) Total outcome = 8741
Number of outcome (N) = 10
Mean = 8741/10 = 874.1
From the provided data table, the following parameters can be deduced (x-u)^2 = 3432426.9
N = 10

√
Apply formula
x
−
u
¿
2
¿
¿
∑
¿
¿
σ
=
√
¿
σ = 3432426.9 =585 .8710
σ =585.87

Depending on the statistics supplied, the “STDEVP” technique in Excel has been used to
validate and merge the computed standard deviation of total medals for each nation, with the
findings presented in the image underneath-
The calculated standard deviation is 585.8691748, while the anticipated standard deviation is
585.87, showing that the addition to actual is accurate and truthful (Sekhar, 2019).
(d) The projected standard deviation may be derived from the spreadsheet that it is crucial in
understanding the predictive method. The standard deviation is a measurement of how far a
given result separates from the mean on average. As a result, a small standard deviation
suggests that the results are approximately normal, whilst a large standard deviation shows that
perhaps the information is more spread. The standard deviation of 585.87 in the given statistics
shows that nations with greater total points are on average 585.87 distant from the project's
mean. The standard deviation in this data may have been used to assess how much several
nations' medal count, like the United States, the Soviet Union, and Australia, vary from the
mean cumulative medal (Silva, 2020).
Question 16
(a) > Appropriately marked graphic to contrast the 10 nations' cumulative gold, silver, and
bronze medals.

Olympic Games Medal Table
1200
1000
800
600
400
200
0
Australia China France Germany Great Britain Hungary Italy Soviet Union Sweden United
States
Counrties participated in the Olympics
Total Games Gold Silver Bronze
(b) The image or graph below depicts a proper and completely marked graph to represent
every nation's difference to the achievement medal.
Number of
medal

Olympic Games Medal Tables
10000
9000
8000
7000
6000
5000
4000
3000
2000
1000
0
1
Contribution of each country to the total medals
Australia China France Germany Great Britain
Hungary Italy Soviet Union Sweden United States
Number of
Medals

Conclusion
This research provided the calculation and assessment of the provided numeracy and IT
knowledge. Mathematics competency is interpreted as the capability to analyse and apply exact
predictive concepts. Fundamental numerical methods, such as dividing, multiplication, addition,
and subtraction, must be understood. Mathematics is required for individuals to develop logical
thought and intellectual abilities in their everyday routines. The concept of numeracy is required
for actions such as dining, giving instructions, assessing bills, and gaming in order to keep
offering answers to problems and to develop understanding of arithmetic, beats, intervals, and
shapes. Literacy and arithmetic are two concepts that really can help people develop the essential
abilities they really have to thrive in society. There is a comprehensive technique for increasing
mathematical and language abilities, and also supporting students in living a pleasant and
fulfilling life and contributing as an active and well-informed community. This mathematics
curriculum is divided into three parts, each of which must be performed separately.

References
Books and journals
Bertheussen, B.A., 2016. Interventions using digital tools to improve students’ engagement and
learning outcomes in higher business education.
Bulteau, J., Feuillet, T. and Dantan, S., 2019. Carpooling and carsharing for commuting in the
Paris region: A comprehensive exploration of the individual and contextual correlates of
their uses. Travel Behaviour and Society, 16, pp.77-87.
Chomicki, G., Schaefer, H. and Renner, S.S., 2020. Origin and domestication of Cucurbitaceae
crops: Insights from phylogenies, genomics and archaeology. New Phytologist, 226(5),
pp.1240-1255.
Danial, J., Feldman, D. and Hutterer, A., 2019. Position estimation of moving objects: Practical
provable approximation. IEEE Robotics and Automation Letters, 4(2), pp.1985-1992.
Doshi, J., Basu, S. and Pang, G., 2018. From satellite imagery to disaster insights. arXiv preprint
arXiv:1812.07033.
Espinosa-Oviedo, J.A., 2020. Enacting Data Science Pipelines for Exploring Graphs: From
Libraries to Studios. In ADBIS, TPDL and EDA 2020 Common Workshops and
Doctoral Consortium: International Workshops: DOING, MADEISD, SKG, BBIGAP,
SIMPDA, AIMinScience 2020 and Doctoral Consortium, Lyon, France, August 25-27,
2020, Proceedings (Vol. 1260, p. 271). Springer Nature.
Hoekman, P. and von Blottnitz, H., 2017. Cape Town’s metabolism: Insights from a material
flow analysis. Journal of Industrial Ecology, 21(5), pp.1237-1249.
Jones, G. and Panova, E., 2018. New insights and long-term safety of tocilizumab in rheumatoid
arthritis. Therapeutic advances in musculoskeletal disease, 10(10), pp.195-199.
Naimipour, B., Guzdial, M. and Shreiner, T., 2020, October. Engaging Pre-Service Teachers in
Front-End Design: Developing Technology for a Social Studies Classroom. In 2020
IEEE Frontiers in Education Conference (FIE) (pp. 1-9). IEEE.
Nitu, P., Coelho, J. and Madiraju, P., 2021. Improvising personalized travel recommendation
system with recency effects. Big Data Mining and Analytics, 4(3), pp.139-154.
Sekhar, A.S., 2019. Diagnostics of actuation system by Hadamard product of integrated motor
current residuals applied to electro-mechanical actuators. International Journal of
Prognostics and Health Management, 10(1).
Silva, J.E.B.D., 2020. Automotive industry in a business model revolution (Doctoral
dissertation).